Saltar al contenido principal
LibreTexts Español

11.5E: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112792

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    La práctica hace la perfección

    Ejercicio\(\PageIndex{13}\) Graph a Hyperbola with Center at \((0,0)\)

    En los siguientes ejercicios, grafica.

    1. \(\frac{x^{2}}{9}-\frac{y^{2}}{4}=1\)
    2. \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\)
    3. \(\frac{x^{2}}{16}-\frac{y^{2}}{25}=1\)
    4. \(\frac{x^{2}}{9}-\frac{y^{2}}{36}=1\)
    5. \(\frac{y^{2}}{25}-\frac{x^{2}}{4}=1\)
    6. \(\frac{y^{2}}{36}-\frac{x^{2}}{16}=1\)
    7. \(16 y^{2}-9 x^{2}=144\)
    8. \(25 y^{2}-9 x^{2}=225\)
    9. \(4 y^{2}-9 x^{2}=36\)
    10. \(16 y^{2}-25 x^{2}=400\)
    11. \(4 x^{2}-16 y^{2}=64\)
    12. \(9 x^{2}-4 y^{2}=36\)
    Contestar

    1.

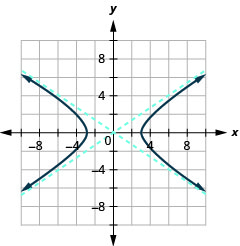
    El gráfico muestra el eje x y el eje y que corren ambos en la dirección negativa y positiva, pero a intervalos sin etiquetar, con asíntotas y es igual a más o menos dos tercios por x, y ramas que pasan por los vértices (más o menos 3, 0) y se abren a izquierda y derecha.
    Figura 11.4.33

    3.

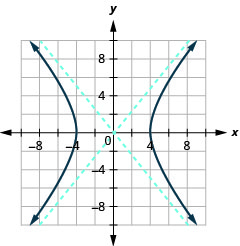
    La gráfica muestra el eje x y el eje y que ambos corren en las direcciones negativa y positiva con asíntotas y es igual a más o menos cinco cuartos por x, y ramas que pasan por los vértices (más o menos 4, 0) y abren a izquierda y derecha.
    Figura 11.4.34

    5.

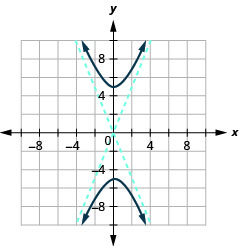
    La gráfica muestra el eje x y el eje y que ambos corren en las direcciones negativa y positiva con asíntotas y es igual a más o menos cinco mitades por x, y ramas que pasan por los vértices (0, más o menos 5) y se abren hacia arriba y hacia abajo.
    Figura 11.4.35

    7.

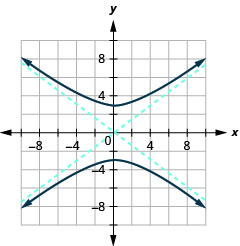
    La gráfica muestra el eje x y el eje y que ambos corren en la dirección negativa y positiva con asíntotas y es igual a más o menos tres cuartos por x, y ramas que pasan por los vértices (0, más o menos 3) y se abren hacia arriba y hacia abajo.
    Figura 11.4.36

    9.

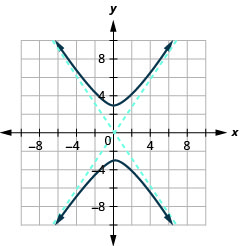
    La gráfica muestra el eje x y el eje y que ambos corren en la dirección negativa y positiva con asíntotas y es igual a más o menos tres mitades por x, y ramas que pasan por los vértices (0, más o menos 3) y se abren hacia arriba y hacia abajo.
    Figura 11.4.37

    11.

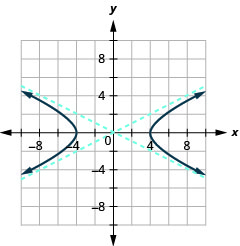
    La gráfica muestra el eje x y el eje y que ambos corren en las direcciones negativa y positiva con asíntotas y es igual a más o menos media veces x, y ramas que pasan por los vértices (más o menos 4, 0) y se abren a izquierda y derecha.
    Figura 11.4.38
    Ejercicio\(\PageIndex{14}\) Graph a Hyperbola with Center at \((h,k)\)

    En los siguientes ejercicios, grafica.

    1. \(\frac{(x-1)^{2}}{16}-\frac{(y-3)^{2}}{4}=1\)
    2. \(\frac{(x-2)^{2}}{4}-\frac{(y-3)^{2}}{16}=1\)
    3. \(\frac{(y-4)^{2}}{9}-\frac{(x-2)^{2}}{25}=1\)
    4. \(\frac{(y-1)^{2}}{25}-\frac{(x-4)^{2}}{16}=1\)
    5. \(\frac{(y+4)^{2}}{25}-\frac{(x+1)^{2}}{36}=1\)
    6. \(\frac{(y+1)^{2}}{16}-\frac{(x+1)^{2}}{4}=1\)
    7. \(\frac{(y-4)^{2}}{16}-\frac{(x+1)^{2}}{25}=1\)
    8. \(\frac{(y+3)^{2}}{16}-\frac{(x-3)^{2}}{36}=1\)
    9. \(\frac{(x-3)^{2}}{25}-\frac{(y+2)^{2}}{9}=1\)
    10. \(\frac{(x+2)^{2}}{4}-\frac{(y-1)^{2}}{9}=1\)
    Contestar

    1.

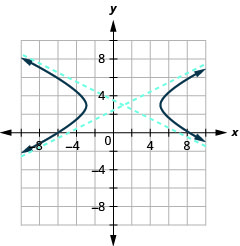
    La gráfica muestra el eje x y el eje y que corren ambos en las direcciones negativa y positiva con el centro (1, 3) una asíntota que pasa por (negativo 3, 1) y (5, 5) y una asíntota que pasa por (5, 1) y (negativo 3, 5), y ramas que pasan por los vértices (negativo 3, 3) y (5, 3) y se abre a izquierda y derecha.
    Figura 11.4.39

    3.

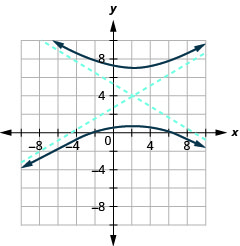
    La gráfica muestra el eje x y el eje y que corren ambos en las direcciones negativa y positiva con el centro (1, 3) una asíntota que pasa por (negativo 3, 1) y (5, 5) y una asíntota que pasa por (5, 1) y (negativo 3, 5), y ramas que pasan por los vértices (negativo 3, 3) y (5, 3) y se abre a izquierda y derecha.
    Figura 11.4.40

    5.

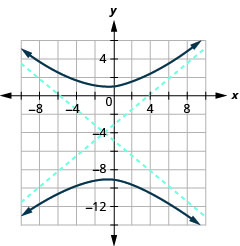
    La gráfica muestra el eje x y el eje y que corren ambos en las direcciones negativa y positiva con el centro (1, negativo 4) una asíntota que pasa por (negativo 7, 1) y (5, negativo 9) y una asíntota que pasa por (5, 1) y (negativo 7, negativo 9), y ramas que pasan por los vértices (1, 1) y (1, negativo 9) y se abren hacia arriba y hacia abajo.
    Figura 11.4.41

    7.

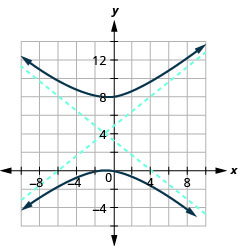
    La gráfica muestra el eje x y el eje y que corren ambos en las direcciones negativa y positiva con el centro (negativo 1, 4) una asíntota que pasa por (4, 8) y (negativo 6, 0) y una asíntota que pasa a través (negativo 6, 8) y (4, 0), y ramas que pasan por los vértices (negativo 1, 0) y ( negativo 1, 8) y abrir hacia arriba y hacia abajo.
    Figura 11.4.42

    9.

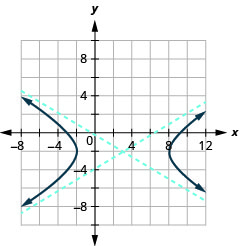
    La gráfica muestra el eje x y el eje y que corren ambos en las direcciones negativa y positiva con el centro (3, negativo 2) una asíntota que pasa por (8, 1) y (negativo 2, negativo 5) y una asíntota que pasa a través (negativo 2, negativo 1) y (8, negativo 5), y ramas que pasan por el vértices (negativo 2, negativo 2) y (8, negativo 2) y abre izquierda y derecha.
    Figura 11.4.43
    Ejercicio\(\PageIndex{15}\) Graph a Hyperbola with Center at \((h,k)\)

    En los siguientes ejercicios,

    1. Escribe la ecuación en forma estándar y
    2. Gráfica.
    1. \(9 x^{2}-4 y^{2}-18 x+8 y-31=0\)
    2. \(16 x^{2}-4 y^{2}+64 x-24 y-36=0\)
    3. \(y^{2}-x^{2}-4 y+2 x-6=0\)
    4. \(4 y^{2}-16 x^{2}-24 y+96 x-172=0\)
    5. \(9 y^{2}-x^{2}+18 y-4 x-4=0\)
    Contestar

    1.

    1. \(\frac{(x-1)^{2}}{4}-\frac{(y-1)^{2}}{9}=1\)
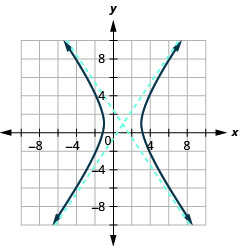
    La gráfica muestra el eje x y el eje y que corren ambos en las direcciones negativa y positiva con el centro (1, 1) una asíntota que pasa por (3, 4) y (negativo 1, negativo 2) y una asíntota que pasa a través de (negativo 1, 4) y (3, negativo 2), y ramas que pasan por los vértices (negativo 1, 1) y (3, 1) y se abre a izquierda y derecha.
    Figura 11.4.44

    3.

    1. \(\frac{(y-2)^{2}}{9}-\frac{(x-1)^{2}}{9}=1\)
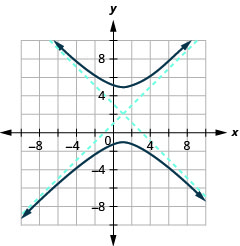
    La gráfica muestra el eje x y el eje y que corren ambos en las direcciones negativa y positiva con el centro (1, 2) una asíntota que pasa por (4, 5) y (negativo 2, negativo 1) y una asíntota que pasa a través (negativo 2, 5) y (4, negativo 1), y ramas que pasan por los vértices (1, 5) y ( 1, negativo 1) y abrir hacia arriba y hacia abajo.
    Figura 11.4.45

    5.

    1. \(\frac{(y+1)^{2}}{1}-\frac{(x+2)^{2}}{9}=1\)
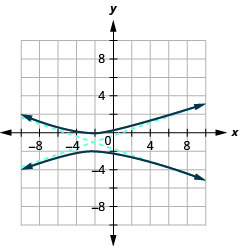
    La gráfica muestra el eje x y el eje y que corren ambos en las direcciones negativa y positiva con el centro (negativo 2, negativo 1) una asíntota que pasa por (1, 0) y (negativo 5, negativo 2) y una asíntota que pasa por (3, 0) y (1, negativo 2), y ramas que pasan por los vértices ( negativo 2, 0) y (negativo 2, negativo 2) y se abren hacia arriba y hacia abajo.
    Figura 11.4.46
    Ejercicio\(\PageIndex{16}\) Identify the Graph of each Equation as a Circle, Parabola, Ellipse, or Hyperbola

    En los siguientes ejercicios, identifica el tipo de gráfica.

      1. \(x=-y^{2}-2 y+3\)
      2. \(9 y^{2}-x^{2}+18 y-4 x-4=0\)
      3. \(9 x^{2}+25 y^{2}=225\)
      4. \(x^{2}+y^{2}-4 x+10 y-7=0\)
      1. \(x=-2 y^{2}-12 y-16\)
      2. \(x^{2}+y^{2}=9\)
      3. \(16 x^{2}-4 y^{2}+64 x-24 y-36=0\)
      4. \(16 x^{2}+36 y^{2}=576\)
    Contestar

    2.

    1. Parábola
    2. Círculo
    3. Hipérbola
    4. Elipse
    Ejercicio\(\PageIndex{17}\) Mixed Practice

    En los siguientes ejercicios, grafica cada ecuación.

    1. \(\frac{(y-3)^{2}}{9}-\frac{(x+2)^{2}}{16}=1\)
    2. \(x^{2}+y^{2}-4 x+10 y-7=0\)
    3. \(y=(x-1)^{2}+2\)
    4. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    5. \((x+2)^{2}+(y-5)^{2}=4\)
    6. \(9 x^{2}-4 y^{2}+54 x+8 y+41=0\)
    7. \(x=-y^{2}-2 y+3\)
    8. \(16 x^{2}+9 y^{2}=144\)
    Contestar

    2.

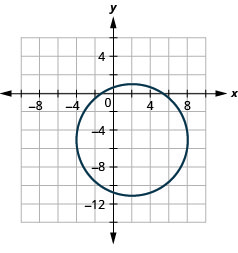
    La gráfica muestra el plano de coordenadas x y con un círculo cuyo centro es (2, negativo 5) y cuyo radio es de 6 unidades.
    Figura 11.4.47

    4.

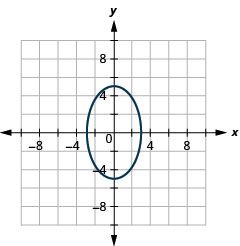
    El gráfico muestra el plano de coordenadas x y con una elipse cuyo eje mayor es vertical, los vértices son (0, más o menos 5) y los co-vértices son (más o menos 3, 0).
    Figura 11.4.48

    6.

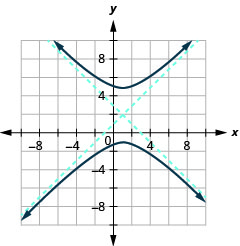
    La gráfica muestra el plano de coordenadas x y con el centro (1, 2) una asíntota que pasa por (negativo 2, 5) y (5, negativo 1) y una asíntota que pasa por (4, 5) y (2, 0), y ramas que pasan por los vértices (1, 5) y (negativo 2, negativo 1) y se abren hacia arriba y hacia abajo.
    Figura 11.4.49

    8.

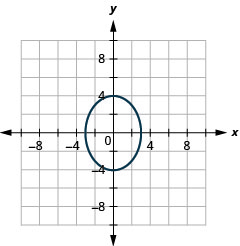
    El gráfico muestra el plano de coordenadas x y con una elipse cuyo eje mayor es vertical, los vértices son (0, más o menos 4) y los co-vértices son (más o menos 3, 0).
    Figura 11.4.50
    Ejercicio\(\PageIndex{18}\) Writing Exercises
    1. En sus propias palabras, defina una hipérbola y escriba la ecuación de una hipérbola centrada en el origen en forma estándar. Dibuja un boceto de la hipérbola etiquetando el centro, vértices y asíntotas.
    2. Explica con tus propias palabras cómo crear y usar el rectángulo que ayuda a graficar una hipérbola.
    3. Comparar y contrastar las gráficas de las ecuaciones\(\frac{x^{2}}{4}-\frac{y^{2}}{9}=1\) y\(\frac{y^{2}}{9}-\frac{x^{2}}{4}=1\).
    4. Explica con tus propias palabras, cómo distinguir la ecuación de una elipse con la ecuación de una hipérbola.
    Contestar

    2. Las respuestas pueden variar

    4. Las respuestas pueden variar

    Autocomprobación

    a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

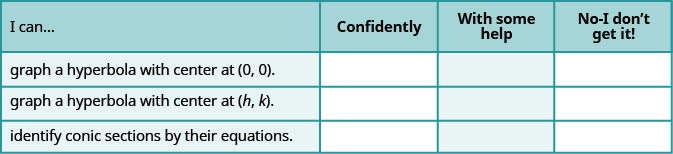
    Esta tabla tiene cuatro columnas y cuatro filas. La primera fila es un encabezado y etiqueta a cada columna, “I can…â€, “confiadamente, ††“Con algo de ayuda, †y †œNo-I don’ t get it! †En la fila 2, el I can fue graficar una hipérbola con centro en (0, 0). En la fila 3, el I can fue graficar una hipérbola con un centro en (h, k). En la fila 4, el I can fue identificar secciones cónicas por sus ecuaciones.
    Figura 11.4.51

    b. En una escala del 1 al 10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?

    This page titled 11.5E: Ejercicios is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform.