11.5: Hipérbolas
- Page ID
- 112787
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Grafica una hipérbola con el centro en\((0,0)\)
- Grafica una hipérbola con el centro en\((h,k)\)
- Identificar secciones conicas por sus ecuaciones
Antes de comenzar, toma este cuestionario de preparación.
- Resolver:\(x^{2}=12\).
Si te perdiste este problema, revisa el Ejemplo 9.1. - Ampliar:\((x−4)^{2}\).
Si te perdiste este problema, revisa el Ejemplo 5.32. - Gráfica\(y=-\frac{2}{3} x\).
Si te perdiste este problema, revisa el Ejemplo 3.4.
Graficar una hipérbola con Centro en\((0,0)\)
La última sección cónica que veremos se llama hipérbola. Veremos que la ecuación de una hipérbola se ve igual que la ecuación de una elipse, excepto que es una diferencia más que una suma. Si bien las ecuaciones de una elipse y una hipérbola son muy similares, sus gráficas son muy diferentes.
Definimos una hipérbola como todos los puntos en un plano donde la diferencia de sus distancias desde dos puntos fijos es constante. Cada uno de los puntos fijos se llama foco de la hipérbola.
Una hipérbola son todos los puntos en un plano donde la diferencia de sus distancias desde dos puntos fijos es constante. Cada uno de los puntos fijos se llama foco de la hipérbola.
La línea a través de los focos, se llama eje transversal. Los dos puntos donde el eje transversal cruza la hipérbola son cada uno un vértice de la hipérbola. El punto medio del segmento que une los focos se llama centro de la hipérbola. La línea perpendicular al eje transversal que pasa por el centro se denomina eje conjugado. Cada pieza de la gráfica se llama una rama de la hipérbola.
Nuevamente nuestro objetivo es conectar la geometría de una cónica con el álgebra. Colocar la hipérbola en un sistema de coordenadas rectangulares nos da esa oportunidad. En la figura, colocamos la hipérbola de manera que los focos\(((−c,0),(c,0))\) están en el\(x\) eje -y el centro es el origen.
La definición establece que la diferencia de la distancia de los focos a un punto\((x,y)\) es constante. Entonces\(|d_{1}−d_{2}|\) es una constante que\(2a\) así llamaremos\(|d_{1}-d_{2} |=2 a\). Usaremos la fórmula de distancia para llevarnos a una fórmula algebraica para una elipse.
\(\left|d_{1} - d_{2}\right| =2 a\)
Usa la fórmula de distancia para encontrar\(d_{1}, d_{2}\)
\(\left|\sqrt{(x-(-c))^{2}+(y-0)^{2}}-\sqrt{(x-c)^{2}+(y-0)^{2}}\right|=2 a\)
Elimina los radicales. Para simplificar la ecuación de la elipse, dejamos\(c^{2}-a^{2}=b^{2}\).
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{c^{2}-a^{2}}=1\)
Entonces, la ecuación de una hipérbola centrada en el origen en forma estándar es:
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Para graficar la hipérbola, será útil conocer las intercepciones. Encontraremos las\(x\) -intercepciones e\(y\) -intercepciones usando la fórmula.
\(x\)-intercepta
Vamos\(y=0\).
\(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}-\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)
Los\(x\) -interceptos son\((a,0)\) y\((−a,0)\).
\(y\)-intercepta
Vamos\(x=0\).
\(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\-\frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=-b^{2} \\ y &=\pm \sqrt{-b^{2}} \end{aligned}\)
No hay\(y\) -intercepciones.
Los\(a, b\) valores de la ecuación también nos ayudan a encontrar las asíntotas de la hipérbola. Las asíntotas son líneas rectas que se cruzan a las que se acercan las ramas de la gráfica pero nunca se cruzan a medida que los\(x, y\) valores se hacen cada vez más grandes.
Para encontrar las asíntotas, esbozamos un rectángulo cuyos lados intersectan el eje x en los vértices\((−a,0),(a,0)\), e intersectamos el\(y\) eje -en\((0,−b), (0,b)\). Las líneas que contienen las diagonales de este rectángulo son las asíntotas de la hipérbola. El rectángulo y las asíntotas no forman parte de la hipérbola, pero nos ayudan a graficar la hipérbola.
Las asíntotas pasan por el origen y podemos evaluar su pendiente usando el rectángulo que dibujamos. Tienen ecuaciones\(y=\frac{b}{a} x\) y\(y=-\frac{b}{a} x\).
Existen dos ecuaciones para las hipérbolas, dependiendo de si el eje transversal es vertical u horizontal. Podemos decir si el eje transversal es horizontal mirando la ecuación. Cuando la ecuación está en forma estándar, si el\(x^{2}\) término es positivo, el eje transversal es horizontal. Cuando la ecuación está en forma estándar, si el\(y^{2}\) término es positivo, el eje transversal es vertical.
Las segundas ecuaciones podrían derivarse de manera similar a lo que hemos hecho. Resumiremos los resultados aquí.
Forma Estándar de la Ecuación a Hipérbola con Centro\((0,0)\)
La forma estándar de la ecuación de una hipérbola con centro\((0,0)\), es
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \quad\)o\(\quad \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)
Observe que, a diferencia de la ecuación de una elipse, el denominador de no siempre\(x^{2}\) es\(a^{2}\) y el denominador de no siempre lo\(y^{2}\) es\(b^{2}\).
Observe que cuando el\(x^{2}\) término es positivo, el eje transversal está en el\(x\) eje. Cuando el\(y^{2}\) término -es positivo, el eje transversal está en el\(y\) eje -eje.
Formas Estándar de la Ecuación a Hipérbola con Centro\((0,0)\)
| \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) | \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\) | |
|---|---|---|
| Orientación | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">Eje transversal sobre el\(x\) eje. Se abre izquierda y derecha |
\ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">Eje transversal sobre el\(y\) eje. Se abre hacia arriba y hacia abajo |
| Vértices | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) | \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\) |
| \(x\)-intercepta | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) | \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">ninguno |
| \(y\)-intercepta | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">ninguno | \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\) |
| Rectángulo | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">Usar\(( \pm a, 0)(0, \pm b)\) | \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">Usar\((0, \pm a)( \pm b, 0)\) |
| Asíntotas | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\(y=\frac{b}{a} x, y=-\frac{b}{a} x\) | \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\(y=\frac{a}{b} x, y=-\frac{a}{b} x\) |
Utilizaremos estas propiedades para graficar hipérbolas.
Gráfica\(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\).
Solución:
| Paso 1: Escribe la ecuación en forma estándar. | La ecuación está en forma estándar. | \(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\) |
| Paso 2: Determinar si el eje transversal es horizontal o vertical. | Dado que el\(x^{2}\) término -es positivo, el eje transversal es horizontal. | El eje transversal es horizontal. |
| Paso 3: Encuentra los vértices. | Desde\(a^{2}=25\) entonces\(a=\pm 5\). Los vértices están en el\(x\) eje. | \((-5,0),(5,0)\) |
| Paso 4: Dibuje el rectángulo centrado en la intersección de origen en un eje\(\pm a\) y el otro en\(\pm b\). |
Ya que\(a=\pm 5\), el rectángulo intersecará el\(x\) eje -en los vértices. Ya que\(b=\pm 2\), el rectángulo se cruzará con el\(y\) eje -en\((0,-2)\) y\((0,2)\). |
.png) |
|
Paso 5: Dibuja las asínticas, las líneas a través de las diagonales del rectángulo. |
Las asíntotas tienen las ecuaciones\(y=\frac{5}{2} x, y=-\frac{5}{2} x\). | .png) |
| Paso 6: Dibuja las dos ramas de la hipérbola. | Comienza en cada vértice y usa las asíntotas como guía. | 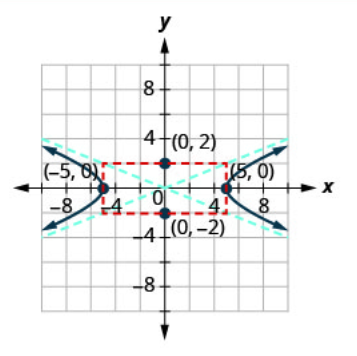.png) |
Gráfica\(\frac{x^{2}}{16}-\frac{y^{2}}{4}=1\).
- Responder
-
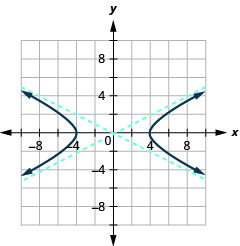
Figura 11.4.9
Gráfica\(\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\).
- Responder
-
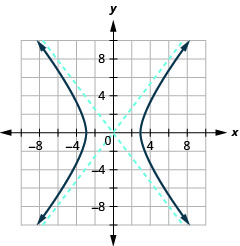
Figura 11.4.10
Resumimos los pasos para referencia.
Graficar una hipérbola centrada en\((0,0)\)
- Escribe la ecuación en forma estándar.
- Determinar si el eje transversal es horizontal o vertical.
- Encuentra los vértices.
- Esboce el rectángulo centrado en el origen intersectando un eje en\(±a\) y el otro en\(±b\).
- Esboce las asíntotas: las líneas a través de las diagonales del rectángulo.
- Dibuja las dos ramas de la hipérbola.
A veces, la ecuación para una hipérbola debe colocarse primero en forma estándar antes de graficarla.
Gráfica\(4 y^{2}-16 x^{2}=64\).
Solución:
| \(4 y^{2}-16 x^{2}=64\) | |
| Para escribir la ecuación en forma estándar, divida cada término por\(64\) para que la ecuación sea igual a\(1\). | \(\frac{4 y^{2}}{64}-\frac{16 x^{2}}{64}=\frac{64}{64}\) |
| Simplificar. | \(\frac{y^{2}}{16}-\frac{x^{2}}{4}=1\) |
| Dado que el\(y^{2}\) término -es positivo, el eje transversal es vertical. Desde\(a^{2}=16\) entonces\(a=\pm 4\). | |
| Los vértices están en el\(y\) eje -,\((0,-a),(0, a)\). Desde\(b^{2}=4\) entonces\(b=\pm 2\). | \((0,-4),(0,4)\) |
| Esboce el rectángulo que interseca el\(x\) eje -en\((-2,0),(2,0)\) y el\(y\) eje -en los vértices. Dibuja las asíntotas a través de las diagonales del rectángulo. Dibuja las dos ramas de la hipérbola. | 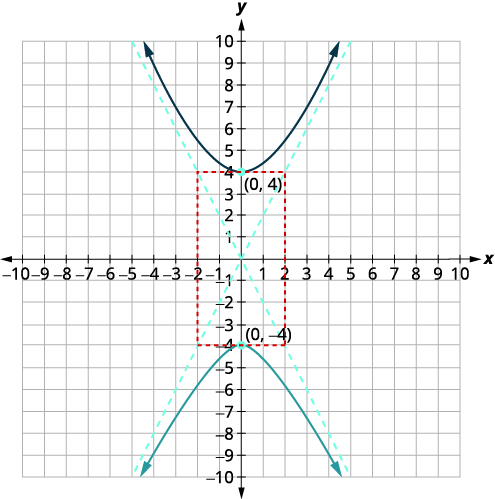 |
Gráfica\(4 y^{2}-25 x^{2}=100\).
- Responder
-
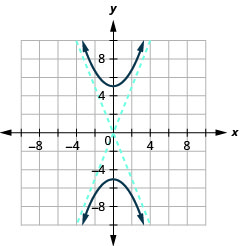
Figura 11.4.12
Gráfica\(25 y^{2}-9 x^{2}=225\).
- Responder
-
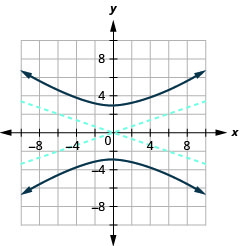
Figura 11.4.13
Graficar una hipérbola con Centro en\((h,k)\)
Las hipérbolas no siempre están centradas en el origen. Cuando una hipérbola se centra en\((h,k)\) las ecuaciones cambia un poco como se refleja en la tabla.
Formas Estándar de la Ecuación a Hipérbola con Centro\((h,k)\)
| \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) | \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\) | |
|---|---|---|
| Orientación | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">El eje transversal es horizontal. Se abre izquierda y derecha | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">El eje transversal es vertical. Se abre hacia arriba y hacia abajo |
| Centro | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">\((h,k)\) | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">\((h,k)\) |
| Vértices | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">\(a\) unidades a la izquierda y derecha del centro | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">\(a\) unidades por encima y por debajo del centro |
| Rectángulo | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">Usar\(a\) unidades izquierda/derecha de\(b\) unidades centrales arriba/debajo del centro | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">Usar\(a\) unidades arriba/debajo de\(b\) las unidades centrales izquierda/derecha del centro |
Gráfica\(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\)
Solución:
| Paso 1: Escribe la ecuación en forma estándar. | La ecuación está en forma estándar. | \(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\) |
| Paso 2: Determinar si el eje transversal es horizontal o vertical. | Dado que el\(x^{2}\) término -es positivo, la hipérbola se abre a izquierda y derecha. | El eje transversal es horizontal. La hipérbola se abre a izquierda y derecha. |
| Paso 3: Encuentra el centro y\(a, b\). | \(h=1\)y\(k=2\) \(a^{2}=9\) \(b^{2}=16\) |
\(\begin{array} {c} \frac{\left(\stackrel{\color{red}{x-h}}{\color{black}{x-1}} \right)^{2}}{9} - \frac{\left(\stackrel{\color{red}{y-k}}{\color{black}{y-2}} \right)^{2}}{16} = 1 \end{array}\) Centro:\((1,2)\) \(a=3\) \(b=4\) |
| Paso 4: Dibuja el rectángulo centrado en el\((h,k)\) uso\(a,b\). |
Marcar el centro,\((1,2)\). Dibuja el rectángulo que atraviesa las\(3\) unidades de puntos hacia la izquierda/derecha del centro y\(4\) las unidades por encima y por debajo del centro. |
.png) |
| Paso 5: Dibuja las asínticas, las líneas a través de las diagonales del rectángulo. Marcar los vértices. | Esboza las diagonales. Marcar los vértices, que están en las\(3\) unidades de rectángulo a la izquierda y derecha del centro. | .png) |
| Paso 6: Dibuja las dos ramas de la hipérbola. | Comienza en cada vértice y usa las asíntotas como guía. | .png) |
Gráfica\(\frac{(x-3)^{2}}{25}-\frac{(y-1)^{2}}{9}=1\).
- Contestar
-
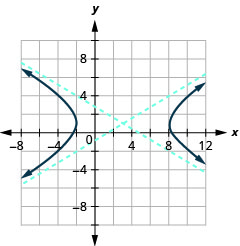
Figura 11.4.17
Gráfica\(\frac{(x-2)^{2}}{4}-\frac{(y-2)^{2}}{9}=1\).
- Contestar
-
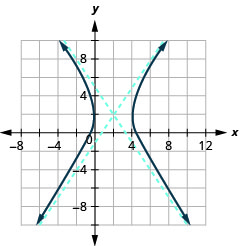
Figura 11.4.18
Resumimos los pasos para una fácil referencia.
Graficar una hipérbola centrada en\((h,k)\)
- Escribe la ecuación en forma estándar.
- Determinar si el eje transversal es horizontal o vertical.
- Encuentra el centro y\(a,b\).
- Esboce el rectángulo centrado en el\((h,k)\) uso\(a,b\).
- Esboce las asíntotas: las líneas a través de las diagonales del rectángulo. Marcar los vértices.
- Dibuja las dos ramas de la hipérbola.
Ten cuidado al identificar el centro. La ecuación estándar tiene\(x−h\) y\(y−k\) con el centro como\((h,k)\).
Gráfica\(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{4}=1\).
Solución:
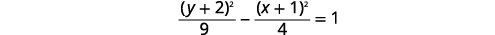 |
|
| Dado que el\(y^{2}\) término -es positivo, la hipérbola se abre hacia arriba y hacia abajo. | 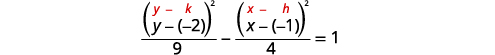 |
| Encuentra el centro,\((h,k)\). | Centro:\((-1,-2)\) |
| Encontrar\(a,b\). | \(a=3 b=2\) |
| Esboza el rectángulo que atraviesa las\(3\) unidades de puntos por encima y por debajo del centro y \(2\) las unidades a la izquierda/derecha del centro. Dibuje las asíntotas: las líneas a través de las diagonales del rectángulo. Marcar los vértices. Grafica las ramas. |
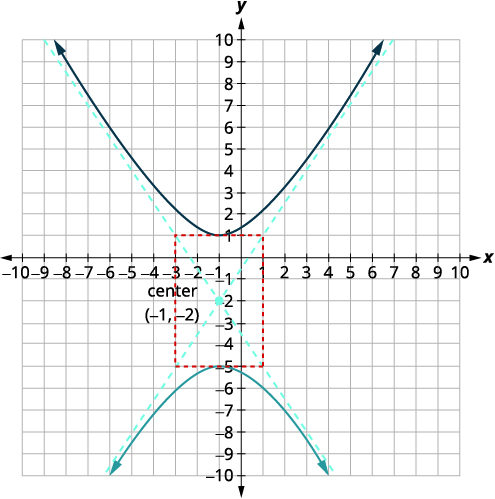 |
Gráfica\(\frac{(y+3)^{2}}{16}-\frac{(x+2)^{2}}{9}=1\).
- Contestar
-
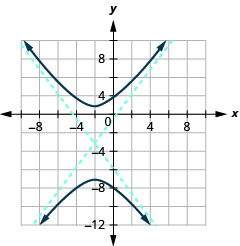
Figura 11.4.22
Gráfica\(\frac{(y+2)^{2}}{9}-\frac{(x+2)^{2}}{9}=1\).
- Contestar
-
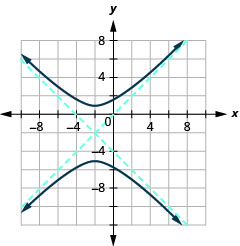
Figura 11.4.23
Nuevamente, a veces tenemos que poner la ecuación en forma estándar como nuestro primer paso.
Escribe la ecuación en forma estándar y grafica\(4 x^{2}-9 y^{2}-24 x-36 y-36=0\).
Solución:
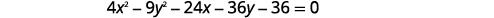 |
|
| Para llegar al formulario estándar, complete los cuadrados. | 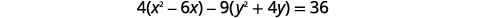 |
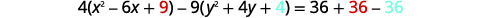 |
|
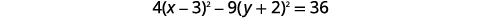 |
|
| Divide cada término por\(36\) para conseguir que la constante sea\(1\). | 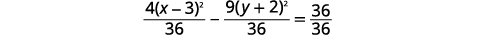 |
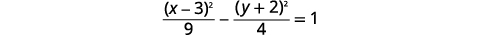 |
|
| Dado que el\(x^{2}\) término -es positivo, la hipérbola se abre a izquierda y derecha. | |
| Encuentra el centro,\((h,k)\). | Centro:\((3, -2)\) |
| Encontrar\(a,b\). |
\(a=3\) \(b=4\) |
| Dibuja el rectángulo que atraviesa las\(3\) unidades de puntos hacia la izquierda/derecha del centro y\(2\) las unidades por encima y por debajo del centro. Dibuje las asíntotas: las líneas a través de las diagonales del rectángulo. Marcar los vértices. Grafica las ramas. |
 |
- Escribe la ecuación en forma estándar y
- Gráfica\(9 x^{2}-16 y^{2}+18 x+64 y-199=0\).
- Contestar
-
- \(\frac{(x+1)^{2}}{16}-\frac{(y-2)^{2}}{9}=1\)
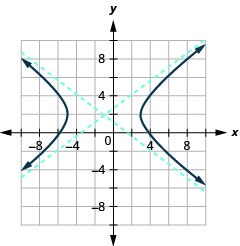
Figura 11.4.31
- Escribe la ecuación en forma estándar y
- Gráfica\(16 x^{2}-25 y^{2}+96 x-50 y-281=0\).
- Contestar
-
- \(\frac{(x+3)^{2}}{25}-\frac{(y+1)^{2}}{16}=1\)
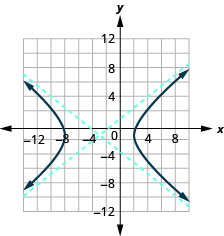
Figura 11.4.32
Identificar secciones Cónicas por sus Ecuaciones
Ahora que hemos completado nuestro estudio de las secciones cónicas, echaremos un vistazo a las diferentes ecuaciones y reconoceremos algunas formas de identificar una cónica por su ecuación. Cuando se nos da una ecuación para graficar, es útil identificar la cónica para que sepamos qué próximos pasos tomar.
Para identificar una cónica a partir de su ecuación, es más fácil si ponemos los términos variables en un lado de la ecuación y las constantes en el otro.
| Cónico | Características de\(x^{2}\) - y\(y^{2}\) -términos | Ejemplo |
|---|---|---|
| Parábola | \ (x^ {2}\) - y\(y^{2}\) -términos">O\(x^{2}\) O\(y^{2}\). Sólo una variable es cuadrada. | \(x=3 y^{2}-2 y+1\) |
| Círculo | \ (x^ {2}\) - y\(y^{2}\) -términos">\(x^{2}\) - y\(y^{2}\) - términos tienen los mismos coeficientes. | \(x^{2}+y^{2}=49\) |
| Elipse | \ (x^ {2}\) - y\(y^{2}\) -términos">\(x^{2}\) - y\(y^{2}\) - términos tienen el mismo signo, diferentes coeficientes. | \(4 x^{2}+25 y^{2}=100\) |
| Hipérbola | \ (x^ {2}\) - y\(y^{2}\) -términos">\(x^{2}\) - y\(y^{2}\) - términos tienen los diferentes signos, diferentes coeficientes. | \(25 y^{2}-4 x^{2}=100\) |
Identificar la gráfica de cada ecuación como círculo, parábola, elipse o hipérbola.
- \(9 x^{2}+4 y^{2}+56 y+160=0\)
- \(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)
- \(x^{2}+y^{2}-6 x-8 y=0\)
- \(y=-2 x^{2}-4 x-5\)
Solución:
a. Los\(y^{2}\) términos\(x^{2}\) - y -tienen el mismo signo y diferentes coeficientes.
\(9 x^{2}+4 y^{2}+56 y+160=0\)
Elipse
b. Los\(y^{2}\) términos\(x^{2}\) - y -tienen signos diferentes y coeficientes diferentes.
\(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)
Hipérbola
c. Los\(y^{2}\) términos\(x^{2}\) - y -tienen los mismos coeficientes.
\(x^{2}+y^{2}-6 x-8 y=0\)
Círculo
d. Sólo una variable\(x\),, es cuadrada.
\(y=-2 x^{2}-4 x-5\)
Parábola
Identificar la gráfica de cada ecuación como círculo, parábola, elipse o hipérbola.
- \(x^{2}+y^{2}-8 x-6 y=0\)
- \(4 x^{2}+25 y^{2}=100\)
- \(y=6 x^{2}+2 x-1\)
- \(16 y^{2}-9 x^{2}=144\)
- Contestar
-
- Círculo
- Elipse
- Parábola
- Hipérbola
Identificar la gráfica de cada ecuación como círculo, parábola, elipse o hipérbola.
- \(16 x^{2}+9 y^{2}=144\)
- \(y=2 x^{2}+4 x+6\)
- \(x^{2}+y^{2}+2 x+6 y+9=0\)
- \(4 x^{2}-16 y^{2}=64\)
- Contestar
-
- Elipse
- Parábola
- Círculo
- Hipérbola
Acceda a estos recursos en línea para obtener instrucciones adicionales y practique con hipérbolas.
- Graficar una hipérbola con el centro en el origen
- Graficar una hipérbola con el centro no en el origen
- Graficar una hipérbola en forma general
- Identificación de secciones cónicas en forma general
Conceptos clave
- Hipérbola: Una hipérbola son todos los puntos en un plano donde la diferencia de sus distancias desde dos puntos fijos es constante.
- Cada uno de los puntos fijos se llama foco de la hipérbola.
La línea a través de los focos, se llama eje transversal.
Los dos puntos donde el eje transversal cruza la hipérbola son cada uno un vértice de la hipérbola.
El punto medio del segmento que une los focos se llama centro de la hipérbola.
La línea perpendicular al eje transversal que pasa por el centro se denomina eje conjugado.
Cada pieza de la gráfica se llama rama de la hipérbola.
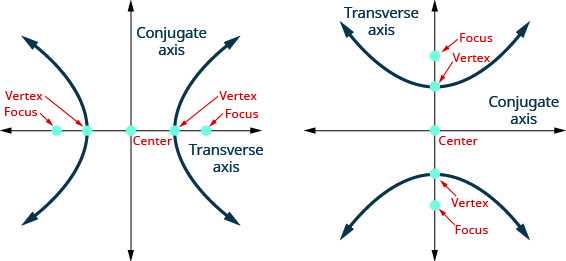
Figura 11.4.2
Formas Estándar de la Ecuación a Hipérbola con Centro\((0,0)\)
| \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) | \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\) | |
|---|---|---|
| Orientación | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">Eje transversal sobre el\(x\) eje. Se abre izquierda y derecha |
\ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">Eje transversal sobre el\(y\) eje. Se abre hacia arriba y hacia abajo |
| Vértices | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) | \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\) |
| \(x\)-intercepta | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) | \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">ninguno |
| \(y\)-intercepta | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">ninguno | \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\) |
| Rectángulo | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">Usar\(( \pm a, 0)(0, \pm b)\) | \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">Usar\((0, \pm a)( \pm b, 0)\) |
| Asíntotas | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\(y=\frac{b}{a} x, y=-\frac{b}{a} x\) | \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\(y=\frac{a}{b} x, y=-\frac{a}{b} x\) |
- Cómo graficar una hipérbola centrada en\((0,0)\).
- Escribe la ecuación en forma estándar.
- Determinar si el eje transversal es horizontal o vertical.
- Encuentra los vértices.
- Esboce el rectángulo centrado en el origen intersectando un eje en\(±a\) y el otro en\(±b\).
- Esboce las asíntotas: las líneas a través de las diagonales del rectángulo.
- Dibuja las dos ramas de la hipérbola.
Formas Estándar de la Ecuación a Hipérbola con Centro\((h,k)\)
| \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) | \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\) | |
|---|---|---|
| Orientación | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">El eje transversal es horizontal. Se abre izquierda y derecha | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">El eje transversal es vertical. Se abre hacia arriba y hacia abajo |
| Centro | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">\((h,k)\) | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">\((h,k)\) |
| Vértices | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">\(a\) unidades a la izquierda y derecha del centro | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">\(a\) unidades por encima y por debajo del centro |
| Rectángulo | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">Usar\(a\) unidades izquierda/derecha de\(b\) unidades centrales arriba/debajo del centro | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">Usar\(a\) unidades arriba/debajo de\(b\) las unidades centrales izquierda/derecha del centro |
- Cómo graficar una hipérbola centrada en\((h,k)\).
- Escribe la ecuación en forma estándar.
- Determinar si el eje transversal es horizontal o vertical.
- Encuentra el centro y\(a,b\).
- Esboce el rectángulo centrado en el\((h,k)\) uso\(a,b\).
- Esboce las asíntotas: las líneas a través de las diagonales del rectángulo. Marcar los vértices.
- Dibuja las dos ramas de la hipérbola.
| Cónico | Características de\(x^{2}\) - y\(y^{2}\) -términos | Ejemplo |
|---|---|---|
| Parábola | \ (x^ {2}\) - y\(y^{2}\) -términos">O\(x^{2}\) O\(y^{2}\). Sólo una variable es cuadrada. | \(x=3 y^{2}-2 y+1\) |
| Círculo | \ (x^ {2}\) - y\(y^{2}\) -términos">\(x^{2}\) - y\(y^{2}\) - términos tienen los mismos coeficientes. | \(x^{2}+y^{2}=49\) |
| Elipse | \ (x^ {2}\) - y\(y^{2}\) -términos">\(x^{2}\) - y\(y^{2}\) - términos tienen el mismo signo, diferentes coeficientes. | \(4 x^{2}+25 y^{2}=100\) |
| Hipérbola | \ (x^ {2}\) - y\(y^{2}\) -términos">\(x^{2}\) - y\(y^{2}\) - términos tienen los diferentes signos, diferentes coeficientes. | \(25 y^{2}-4 x^{2}=100\) |
Glosario
- hipérbola
- Una hipérbola se define como todos los puntos de un plano donde la diferencia de sus distancias desde dos puntos fijos es constante.


