Saltar al contenido principal
LibreTexts Español

Capítulo 11 Ejercicios de revisión

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112781

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Ejercicios de revisión de capítulos

    Fórmulas de distancia y punto medio; Círculos

    Ejercicio\(\PageIndex{1}\) Use the Distance Formula

    En los siguientes ejercicios, encuentra la distancia entre los puntos. Redondear a la décima más cercana si es necesario.

    1. \((-5,1)\)y\((-1,4)\)
    2. \((-2,5)\)y\((1,5)\)
    3. \((8,2)\)y\((-7,-3)\)
    4. \((1,-4)\)y\((5,-5)\)
    Responder

    2. \(d=3\)

    4. \(d=\sqrt{17}, d \approx 4.1\)

    Ejercicio\(\PageIndex{2}\) Use the Midpoint Formula

    En los siguientes ejercicios, encuentra el punto medio de los segmentos de línea cuyos extremos se dan.

    1. \((-2,-6)\)y\((-4,-2)\)
    2. \((3,7)\)y\((5,1)\)
    3. \((-8,-10)\)y\((9,5)\)
    4. \((-3,2)\)y\((6,-9)\)
    Responder

    2. \((4,4)\)

    4. \(\left(\frac{3}{2},-\frac{7}{2}\right)\)

    Ejercicio\(\PageIndex{3}\) Write the Equation of a Circle in Standard Form

    En los siguientes ejercicios, escriba la forma estándar de la ecuación del círculo con la información dada.

    1. el radio es\(15\) y el centro es\((0,0)\)
    2. el radio es\(\sqrt{7}\) y el centro es\((0,0)\)
    3. el radio es\(9\) y el centro es\((-3,5)\)
    4. el radio es\(7\) y el centro es\((-2,-5)\)
    5. centro es\((3,6)\) y un punto en el círculo es\((3,-2)\)
    6. centro es\((2,2)\) y un punto en el círculo es\((4,4)\)
    Responder

    2. \(x^{2}+y^{2}=7\)

    4. \((x+2)^{2}+(y+5)^{2}=49\)

    6. \((x-2)^{2}+(y-2)^{2}=8\)

    Ejercicio\(\PageIndex{4}\) Graph a Circle

    En los siguientes ejercicios,

    1. Encuentra el centro y el radio, luego
    2. Grafica cada círculo.
    1. \(2 x^{2}+2 y^{2}=450\)
    2. \(3 x^{2}+3 y^{2}=432\)
    3. \((x+3)^{2}+(y-5)^{2}=81\)
    4. \((x+2)^{2}+(y+5)^{2}=49\)
    5. \(x^{2}+y^{2}-6 x-12 y-19=0\)
    6. \(x^{2}+y^{2}-4 y-60=0\)
    Responder

    2.

    1. radio:\(12,\) centro:\((0,0)\)
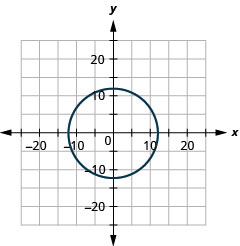
    La figura muestra un círculo graficado en el plano de coordenadas x y. El eje x del plano va de 20 a 20 negativos. El eje y del plano va de negativo 15 a 15. El centro del círculo es (0, 0) y el radio del círculo es 12.
    Figura 11.E.1

    4.

    1. radio:\(7,\) centro:\((-2,-5)\)
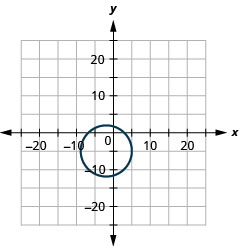
    La figura muestra un círculo graficado en el plano de coordenadas x y. El eje x del plano va de 20 a 20 negativos. El eje y del plano va de negativo 15 a 15. El centro del círculo es (negativo 2, negativo 5) y el radio del círculo es 7.
    Figura 11.E.2

    6.

    1. radio:\(8,\) centro:\((0,2)\)
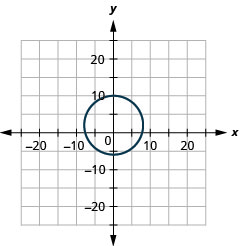
    La figura muestra un círculo graficado en el plano de coordenadas x y. El eje x del plano va de 20 a 20 negativos. El eje y del plano va de negativo 15 a 15. El centro del círculo es (0, 2) y el radio del círculo es 8.
    Figura 11.E.3

    Parábolas

    Ejercicio\(\PageIndex{5}\) Graph Vertical Parabolas

    En los siguientes ejercicios, grafica cada ecuación usando sus propiedades.

    1. \(y=x^{2}+4 x-3\)
    2. \(y=2 x^{2}+10 x+7\)
    3. \(y=-6 x^{2}+12 x-1\)
    4. \(y=-x^{2}+10 x\)
    Responder

    2.

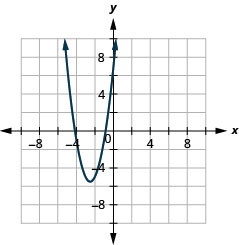
    La figura muestra una parábola de apertura ascendente graficada en el plano de coordenadas x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 7 a 7. El vértice es (cinco mitades negativas, once mitades negativas) y la parábola pasa por los puntos (negativo 4, negativo 1) y (negativo 1, negativo 1).
    Figura 11.E.4

    4.

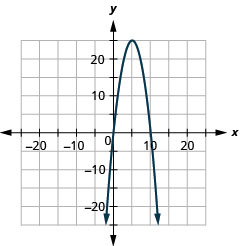
    La figura muestra una parábola de apertura hacia abajo graficada en el plano de coordenadas x y. El eje x del plano va desde el 36 negativo hasta el 36. El eje y del plano va de 26 a 26 negativos. El vértice es (5, 25) y la parábola pasa por los puntos (2, 16) y (8, 16).
    Figura 11.E.5
    Ejercicio\(\PageIndex{6}\) Graph Vertical Parabolas

    En los siguientes ejercicios,

    1. Escribe la ecuación en forma estándar, luego
    2. Utilice las propiedades de la forma estándar para graficar la ecuación.
    1. \(y=x^{2}+4 x+7\)
    2. \(y=2 x^{2}-4 x-2\)
    3. \(y=-3 x^{2}-18 x-29\)
    4. \(y=-x^{2}+12 x-35\)
    Responder

    2.

    1. \(y=2(x-1)^{2}-4\)
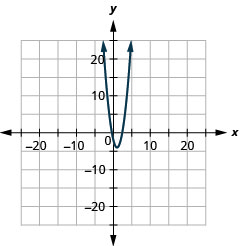
    La figura muestra una parábola de apertura ascendente graficada en el plano de coordenadas x y. El eje x del plano va del negativo 22 al 22. El eje y del plano va de 16 a 16 negativos. El vértice es (1, negativo 4) y la parábola pasa por los puntos (0, negativo 2) y (2, negativo 2).
    Figura 11.E.6

    4.

    1. \(y=-(x-6)^{2}+1\)
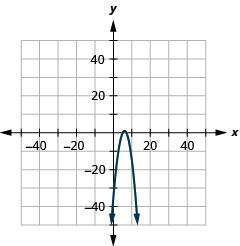
    La figura muestra una parábola de apertura hacia abajo graficada en el plano de coordenadas x y. El eje x del plano va desde el 60 negativo hasta el 60. El eje y del plano va desde el 46 negativo hasta el 46. El vértice es (6, 1) y la parábola pasa por los puntos (5, 0) y (7, 0).
    Figura 11.E.7
    Ejercicio\(\PageIndex{7}\) Graph Horizontal Parabolas

    En los siguientes ejercicios, grafica cada ecuación usando sus propiedades.

    1. \(x=2 y^{2}\)
    2. \(x=2 y^{2}+4 y+6\)
    3. \(x=-y^{2}+2 y-4\)
    4. \(x=-3 y^{2}\)
    Responder

    2.

    La figura muestra una parábola de apertura hacia la derecha graficada en el plano de coordenadas x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 8 a 8. El vértice es (4, negativo 1) y la parábola pasa por los puntos (6, 0) y (6, negativo 2).
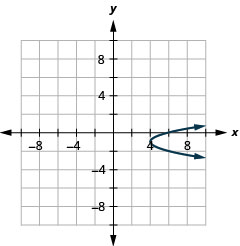
    Figura 11.E.8

    4.

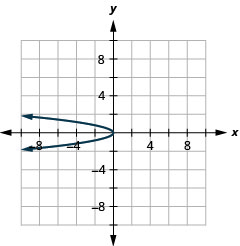
    La figura muestra una parábola de apertura hacia la izquierda graficada en el plano de coordenadas x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 8 a 8. El vértice es (0, 0) y la parábola pasa por los puntos (negativo 3, 1) y (negativo 3, negativo 1).
    Figura 11.E.9
    Ejercicio\(\PageIndex{8}\) Graph Horizontal Parabolas

    En los siguientes ejercicios,

    1. Escribe la ecuación en forma estándar, luego
    2. Utilice las propiedades de la forma estándar para graficar la ecuación.
    1. \(x=4 y^{2}+8 y\)
    2. \(x=y^{2}+4 y+5\)
    3. \(x=-y^{2}-6 y-7\)
    4. \(x=-2 y^{2}+4 y\)
    Responder

    2.

    1. \(x=(y+2)^{2}+1\)
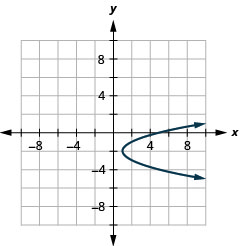
    La figura muestra una parábola de apertura hacia la derecha graficada en el plano de coordenadas x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 8 a 8. El vértice es (1, negativo 2) y la parábola pasa por los puntos (5, 0) y (5, negativo 4).
    Figura 11.E.10

    4.

    1. \(x=-2(y-1)^{2}+2\)
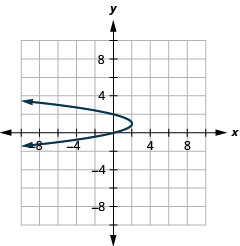
    La figura muestra una parábola de apertura hacia la izquierda graficada en el plano de coordenadas x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 8 a 8. El vértice es (2, negativo 3) y la parábola pasa por los puntos (0, 2) y (0, 0).
    Figura 11.E.11
    Ejercicio\(\PageIndex{9}\) Solve Applications with Parabolas

    En los siguientes ejercicios, crear la ecuación del arco parabólico formado en la cimentación del puente mostrado. Dar la respuesta en forma estándar.

    1.

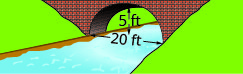
    La figura muestra un arco parabólico formado en la cimentación del puente. El arco mide 5 pies de alto y 20 pies de ancho.
    Figura 11.E.12

    2.

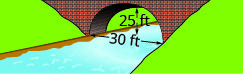
    La figura muestra un arco parabólico formado en la cimentación del puente. El arco mide 25 pies de alto y 30 pies de ancho.
    Figura 11.E.13
    Responder

    2. \(y=-\frac{1}{9} x^{2}+\frac{10}{3} x\)

    Elipses

    Ejercicio\(\PageIndex{10}\) Graph an Ellipse with Center at the Origin

    En los siguientes ejercicios, grafica cada elipse.

    1. \(\frac{x^{2}}{36}+\frac{y^{2}}{25}=1\)
    2. \(\frac{x^{2}}{4}+\frac{y^{2}}{81}=1\)
    3. \(49 x^{2}+64 y^{2}=3136\)
    4. \(9 x^{2}+y^{2}=9\)
    Responder

    2.

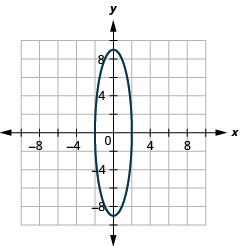
    La figura muestra una elipse graficada en el plano de coordenadas x y. El eje x del plano va de 14 negativo a 14. El eje y del plano va de negativo 10 a 10. La elipse tiene un centro en (0, 0), un eje mayor vertical, vértices en (0, más o menos 9) y comvértices en (más o menos 2, 0).
    Figura 11.E.14

    4.

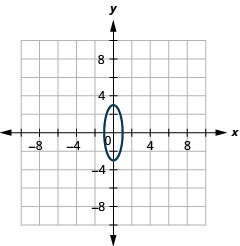
    La figura muestra una elipse graficada en el plano de coordenadas x y. El eje x del plano va desde el 9 negativo hasta el 9. El eje y del plano va de negativo 7 a 7. La elipse tiene un centro en (0, 0), un eje mayor vertical, vértices en (0, más o menos 3) y comvértices en (más o menos 1, 0).
    Figura 11.E.15
    Ejercicio\(\PageIndex{11}\) Find the Equation of an Ellipse with Center at the Origin

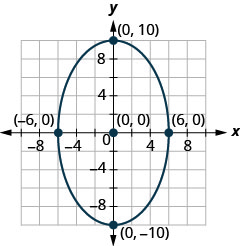
    En los siguientes ejercicios, encuentra la ecuación de la elipse que se muestra en la gráfica.

    1.

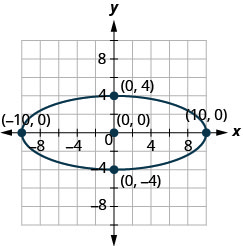
    La figura muestra una elipse graficada en el plano de coordenadas x y. La elipse tiene un centro en (0, 0), un eje mayor horizontal, vértices en (más o menos 10, 0) y comvértices en (0, más o menos 4).
    Figura 11.E.16

    2.

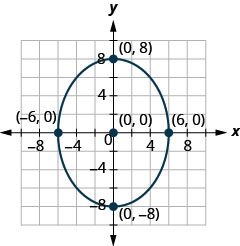
    La figura muestra una elipse graficada en el plano de coordenadas x y. La elipse tiene un centro en (0, 0), un eje mayor vertical, vértices en (0, más o menos 8) y comvértices en (más o menos 6, 0).
    Figura 11.E.17
    Responder

    2. \(\frac{x^{2}}{36}+\frac{y^{2}}{64}=1\)

    Ejercicio\(\PageIndex{12}\) Graph an Ellipse with Center Not at the Origin

    En los siguientes ejercicios, grafica cada elipse.

    1. \(\frac{(x-1)^{2}}{25}+\frac{(y-6)^{2}}{4}=1\)
    2. \(\frac{(x+4)^{2}}{16}+\frac{(y+1)^{2}}{9}=1\)
    3. \(\frac{(x-5)^{2}}{16}+\frac{(y+3)^{2}}{36}=1\)
    4. \(\frac{(x+3)^{2}}{9}+\frac{(y-2)^{2}}{25}=1\)
    Responder

    2.

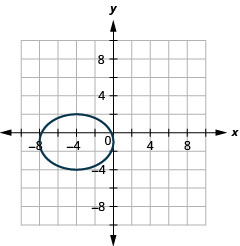
    La figura muestra una elipse graficada en el plano de coordenadas x y. El eje x del plano va de 14 negativo a 14. El eje y del plano va de negativo 10 a 10. La elipse tiene un centro en (negativo 4, negativo 1), un eje mayor horizontal, vértices en (negativo 8, negativo 1) y (0, negativo 1) y co-vértices en (negativo 4, 2) y (negativo 4, negativo 4).
    Figura 11.E.18

    4.

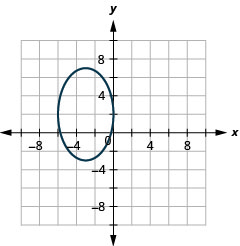
    La figura muestra una elipse graficada en el plano de coordenadas x y. El eje x del plano va de 14 negativo a 14. El eje y del plano va de negativo 10 a 10. La elipse tiene un centro en (negativo 3, 2), un eje mayor vertical, vértices en (negativo 3, 7) y (negativo 3, negativo 3) y co-vértices en (negativo 6, 2) y (0, 2).
    Figura 11.E.19
    Ejercicio\(\PageIndex{13}\) Graph an Ellipse with Center Not at the Origin

    En los siguientes ejercicios,

    1. Escribe la ecuación en forma estándar y
    2. Gráfica.
    1. \(x^{2}+y^{2}+12 x+40 y+120=0\)
    2. \(25 x^{2}+4 y^{2}-150 x-56 y+321=0\)
    3. \(25 x^{2}+4 y^{2}+150 x+125=0\)
    4. \(4 x^{2}+9 y^{2}-126 x+405=0\)
    Responder

    2.

    1. \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
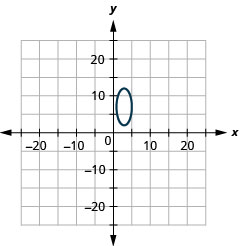
    La figura muestra una elipse graficada en el plano de coordenadas x y. El eje x del plano va de 18 a 18 negativos. El eje y del plano va de 14 a 14 negativos. La elipse tiene un centro en (3, 7), un eje mayor vertical, vértices en (3, 2) y (3, 12) y co-vértices en (negativos 1, 7) y (5, 7).
    Figura 11.E.20

    4.

    1. \(\frac{x^{2}}{9}+\frac{(y-7)^{2}}{4}=1\)
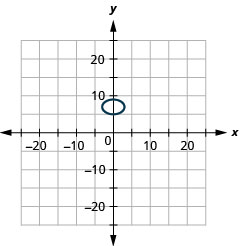
    La figura muestra una elipse graficada en el plano de coordenadas x y. El eje x del plano va de negativo 15 a 15. El eje y del plano va del negativo 11 al 11. La elipse tiene un centro en (0, 7), un eje mayor horizontal, vértices en (3, 7) y (negativo 3, 7) y co-vértices en (0, 5) y (0, 9).
    Figura 11.E.21
    Ejercicio\(\PageIndex{14}\) Solve Applications with Ellipses

    En los siguientes ejercicios, escribe la ecuación de la elipse descrita.

    1. Un cometa se mueve en órbita elíptica alrededor de un sol. Lo más cerca que el cometa llega al sol es aproximadamente\(10\) AU y el más alejado es aproximadamente\(90\) AU. El sol es uno de los focos de la órbita elíptica. Dejando que la elipse se centre en el origen y etiquetando los ejes en AU, la órbita se verá como la figura de abajo. Usa la gráfica para escribir una ecuación para la órbita elíptica del cometa.
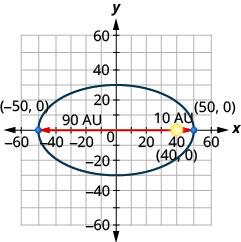
    La figura muestra un modelo de una órbita elíptica alrededor del sol en el plano de coordenadas x y. La elipse tiene un centro en (0, 0), un eje mayor horizontal, vértices marcados en (más o menos 50, 0), el sol marcado como focos y etiquetado (50, 0), la distancia más cercana al que está el cometa del sol marcado como 10 A U, y lo más alejado un cometa es del sol marcado como 90 A U.
    Figura 11.E.22
    Responder

    1. Resolver

    Hipérbolas

    Ejercicio\(\PageIndex{15}\) Graph a Hyperbola with Center at \((0,0)\)

    En los siguientes ejercicios, grafica.

    1. \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\)
    2. \(\frac{y^{2}}{49}-\frac{x^{2}}{16}=1\)
    3. \(9 y^{2}-16 x^{2}=144\)
    4. \(16 x^{2}-4 y^{2}=64\)
    Responder

    1.

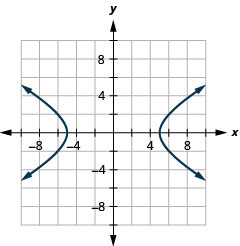
    La figura muestra una hipérbola graficada en el plano de coordenadas x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va desde el 9 negativo hasta el 9. La hipérbola tiene un centro en (0, 0) y ramas que pasan por los vértices (más o menos 5, 0), y que se abren a izquierda y derecha.
    Figura 11.E.23

    3.

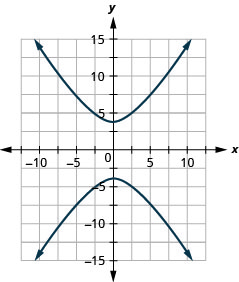
    La figura muestra una hipérbola graficada en el plano de coordenadas x y. El eje x del plano va del negativo 19 al 19. El eje y del plano va de negativo 15 a 15. La hipérbola tiene un centro en (0, 0) y ramas que pasan por los vértices (0, más o menos 4), y que se abren hacia arriba y hacia abajo.
    Figura 11.E.24
    Ejercicio\(\PageIndex{16}\) Graph a Hyperbola with Center at \((h,k)\)

    En los siguientes ejercicios, grafica.

    1. \(\frac{(x+1)^{2}}{4}-\frac{(y+1)^{2}}{9}=1\)
    2. \(\frac{(x-2)^{2}}{4}-\frac{(y-3)^{2}}{16}=1\)
    3. \(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{9}=1\)
    4. \(\frac{(y-1)^{2}}{25}-\frac{(x-2)^{2}}{9}=1\)
    Responder

    1.

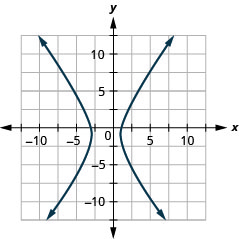
    La figura muestra una hipérbola graficada en el plano de coordenadas x y. El eje x del plano va de 14 negativo a 14. El eje y del plano va de negativo 10 a 10. La hipérbola tiene un centro en (negativo 1, negativo 1) y ramas que pasan por los vértices (negativo 3, negativo 1) y (1, negativo 1), y que se abren a izquierda y derecha.
    Figura 11.E.25

    3.

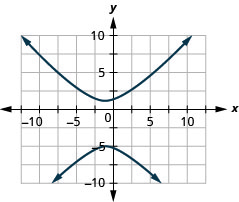
    La figura muestra una hipérbola graficada en el plano de coordenadas x y. El eje x del plano va de 14 negativo a 14. El eje y del plano va de negativo 10 a 10. La hipérbola tiene un centro en (negativo 1, negativo 2) y ramas que pasan por los vértices (negativo 1, 1) y (negativo 1, negativo 5), y que se abren hacia arriba y hacia abajo.
    Figura 11.E.26
    Ejercicio\(\PageIndex{17}\) Graph a Hyperbola with Center at \((h,k)\)

    En los siguientes ejercicios,

    1. Escribe la ecuación en forma estándar y
    2. Gráfica.
    1. \(4 x^{2}-16 y^{2}+8 x+96 y-204=0\)
    2. \(16 x^{2}-4 y^{2}-64 x-24 y-36=0\)
    3. \(4 y^{2}-16 x^{2}+32 x-8 y-76=0\)
    4. \(36 y^{2}-16 x^{2}-96 x+216 y-396=0\)
    Responder

    1.

    1. \(\frac{(x+1)^{2}}{16}-\frac{(y-3)^{2}}{4}=1\)
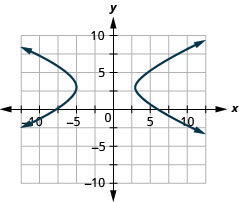
    La figura muestra una hipérbola graficada en el plano de coordenadas x y. El eje x del plano va de 14 negativo a 14. El eje y del plano va de negativo 10 a 10. La hipérbola tiene un centro en (negativo 1, 3) y ramas que pasan por los vértices (negativo 5, 3) y (3, 3), y que se abren a izquierda y derecha.
    Figura 11.E.27

    3.

    1. \(\frac{(y-1)^{2}}{16}-\frac{(x-1)^{2}}{4}=1\)
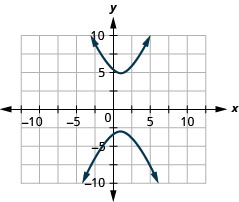
    La figura muestra una hipérbola graficada en el plano de coordenadas x y. El eje x del plano va de 14 negativo a 14. El eje y del plano va de negativo 10 a 10. La hipérbola tiene un centro en (1, 1) y ramas que pasan por los vértices (1, negativo 3) y (1, 5), y que se abren hacia arriba y hacia abajo.
    Figura 11.E.28
    Ejercicio\(\PageIndex{18}\) Identify the Graph of Each Equation as a Circle, Parabola, Ellipse, or Hyperbola

    En los siguientes ejercicios, identifica el tipo de gráfica.

      1. \(16 y^{2}-9 x^{2}-36 x-96 y-36=0\)
      2. \(x^{2}+y^{2}-4 x+10 y-7=0\)
      3. \(y=x^{2}-2 x+3\)
      4. \(25 x^{2}+9 y^{2}=225\)
      1. \(x^{2}+y^{2}+4 x-10 y+25=0\)
      2. \(y^{2}-x^{2}-4 y+2 x-6=0\)
      3. \(x=-y^{2}-2 y+3\)
      4. \(16 x^{2}+9 y^{2}=144\)
    Responder

    1.

    1. Hipérbola
    2. Círculo
    3. Parábola
    4. Elipse

    Resolver Sistemas de Ecuaciones No Lineales

    Ejercicio\(\PageIndex{19}\) Solve a System of Nonlinear Equations Using Graphing

    En los siguientes ejercicios, resuelve el sistema de ecuaciones mediante la gráfica.

    1. \(\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y=-5}\end{array}\right.\)
    Responder

    1.

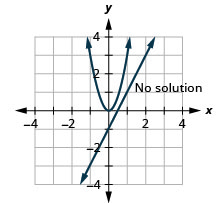
    La figura muestra una parábola y una línea graficada en el plano de coordenadas x y. El eje x del plano va de negativo 5 a 5. El eje y del plano va de negativo 4 a 4. La parábola tiene un vértice en (0, 0) y se abre hacia arriba. La línea tiene una pendiente de 2 con una intersección y en negativo 1. La parábola y la línea no se cruzan, por lo que el sistema no tiene solución.
    Figura 11.E.29

    3.

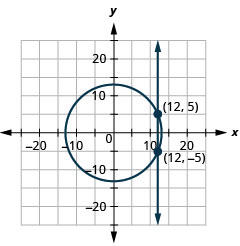
    La figura muestra un círculo y una línea graficados en el plano de coordenadas x y. El eje x del plano va de 20 a 20 negativos. El eje y del plano va de negativo 15 a 15. El círculo tiene un centro en (0, 0) y un radio de 13. La línea es vertical. El círculo y la línea se cruzan en los puntos (12, 5) y (12, negativo 5), que están etiquetados. La solución del sistema es (12, 5) y (12, negativo 5)
    Figura 11.E.30
    Ejercicio\(\PageIndex{20}\) Solve a System of Nonlinear Equations Using Substitution

    En los siguientes ejercicios, resolver el sistema de ecuaciones mediante la sustitución.

    1. \(\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=-2 x+2}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x-y=4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {y-x=5}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {2 x-y=1}\end{array}\right.\)
    Responder

    1. \((-1,4)\)

    3. Sin solución

    Ejercicio\(\PageIndex{21}\) Solve a System of Nonlinear Equations Using Elimination

    En los siguientes ejercicios, resuelve el sistema de ecuaciones mediante el uso de la eliminación.

    1. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y-1=0}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}-y^{2}=5} \\ {-2 x^{2}-3 y^{2}=-30}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {3 y^{2}-4 x=12}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=14} \\ {x^{2}-y^{2}=16}\end{array}\right.\)
    Responder

    1. \((-\sqrt{7}, 3),(\sqrt{7}, 3)\)

    3. \((-3,0),(0,-2),(0,2)\)

    Ejercicio\(\PageIndex{22}\) Use a System of Nonlinear Equations to Solve Applications

    En los siguientes ejercicios, resolver el problema utilizando un sistema de ecuaciones.

    1. La suma de los cuadrados de dos números es\(25\). La diferencia de los números es\(1\). Encuentra los números.
    2. La diferencia de los cuadrados de dos números es\(45\). La diferencia del cuadrado del primer número y dos veces el cuadrado del segundo número es\(9\). Encuentra los números.
    3. El perímetro de un rectángulo es de\(58\) metros y su área es de metros\(210\) cuadrados. Encuentra el largo y ancho del rectángulo.
    4. Colton compró un microondas más grande para su cocina. La diagonal del frente del microondas mide\(34\) pulgadas. El frente también tiene un área de pulgadas\(480\) cuadradas. ¿Cuál es el largo y ancho del microondas?
    Responder

    1. \(-3\)y\(-4\) o\(4\) y\(3\)

    3. Si el largo es\(14\) pulgadas, el ancho es\(15\) pulgadas. Si el largo es\(15\) pulgadas, el ancho es\(14\) pulgadas.

    Prueba de práctica

    Ejercicio\(\PageIndex{23}\)

    En los siguientes ejercicios, encuentra la distancia entre los puntos y el punto medio del segmento de línea con los extremos dados. Redondear a la décima más cercana según sea necesario.

    1. \((-4,-3)\)y\((-10,-11)\)
    2. \((6,8)\)y\((-5,-3)\)
    Responder

    1. distancia:\(10,\) punto medio:\((-7,-7)\)

    Ejercicio\(\PageIndex{24}\)

    En los siguientes ejercicios, escriba la forma estándar de la ecuación del círculo con la información dada.

    1. el radio es\(11\) y el centro es\((0,0)\)
    2. el radio es\(12\) y el centro es\((10,-2)\)
    3. centro es\((-2,3)\) y un punto en el círculo es\((2,-3)\)
    4. Encuentra la ecuación de la elipse que se muestra en la gráfica.
    La figura muestra una elipse graficada en el plano de coordenadas x y. La elipse tiene un centro en (0, 0), un eje mayor vertical, vértices en (0, más o menos 10) y comvértices en (más o menos 6, 0).
    Figura 11.E.31
    Responder

    1. \(x^{2}+y^{2}=121\)

    3. \((x+2)^{2}+(y-3)^{2}=52\)

    Ejercicio\(\PageIndex{25}\)

    En los siguientes ejercicios,

    1. Identificar el tipo de gráfico de cada ecuación como círculo, parábola, elipse o hipérbola, y
    2. Grafica la ecuación.
    1. \(4 x^{2}+49 y^{2}=196\)
    2. \(y=3(x-2)^{2}-2\)
    3. \(3 x^{2}+3 y^{2}=27\)
    4. \(\frac{y^{2}}{100}-\frac{x^{2}}{36}=1\)
    5. \(\frac{x^{2}}{16}+\frac{y^{2}}{81}=1\)
    6. \(x=2 y^{2}+10 y+7\)
    7. \(64 x^{2}-9 y^{2}=576\)
    Responder

    1.

    1. Elipse
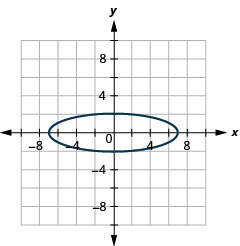
    La figura muestra una elipse graficada en el plano de coordenadas x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 8 a 8. La elipse tiene un centro en (0, 0), un eje mayor horizontal, vértices en (más o menos 7, 0) y co-vértices en (0, más o menos 2).
    Figura 11.E.32

    3.

    1. Círculo
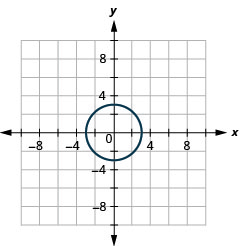
    La figura muestra un círculo graficado en el plano de coordenadas x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 8 a 8. El círculo de parábola tiene un centro en (0, 0) y un radio de 3.
    Figura 11.E.33

    5.

    1. Elipse
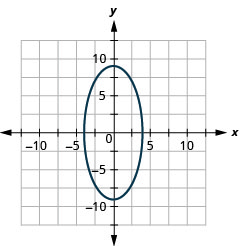
    La figura muestra una elipse graficada en el plano de coordenadas x y. El eje x del plano va de 14 negativo a 14. El eje y del plano va de negativo 10 a 10. La elipse tiene un centro en (0, 0), un eje mayor vertical, vértices en (0, más o menos 9) y co-vértices en (más o menos 4, 0).
    Figura 11.E.34

    7.

    1. Hipérbola
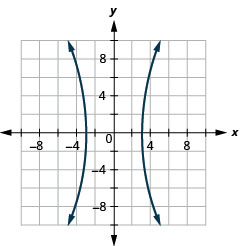
    La figura muestra una hipérbola graficada en el plano de coordenadas x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 8 a 8. La hipérbola tiene un centro en (0, 0) y ramas que pasan por los vértices (más o menos 3, 0) y que se abren a izquierda y derecha.
    Figura 11.E.35
    Ejercicio\(\PageIndex{26}\)

    En los siguientes ejercicios,

    1. Identificar el tipo de gráfica de cada ecuación como círculo, parábola, elipse o hipérbola,
    2. Escriba la ecuación en forma estándar, y
    3. Grafica la ecuación.
    1. \(25 x^{2}+64 y^{2}+200 x-256 y-944=0\)
    2. \(x^{2}+y^{2}+10 x+6 y+30=0\)
    3. \(x=-y^{2}+2 y-4\)
    4. \(9 x^{2}-25 y^{2}-36 x-50 y-214=0\)
    5. \(y=x^{2}+6 x+8\)
    6. Resolver el sistema no lineal de ecuaciones graficando:\(\left\{\begin{array}{l}{3 y^{2}-x=0} \\ {y=-2 x-1}\end{array}\right.\).
    7. Resolver el sistema no lineal de ecuaciones mediante sustitución:\(\left\{\begin{array}{l}{x^{2}+y^{2}=8} \\ {y=-x-4}\end{array}\right.\).
    8. Resolver el sistema no lineal de ecuaciones usando eliminación:\(\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.\)
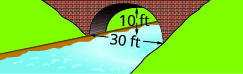
    9. Crear la ecuación del arco parabólico formado en la cimentación del puente mostrado. Dar la respuesta en\(y=a x^{2}+b x+c\) forma.
    La figura muestra un arco parabólico formado en la cimentación del puente. El arco mide 10 pies de alto y 30 pies de ancho.
    Figura 11.E.36

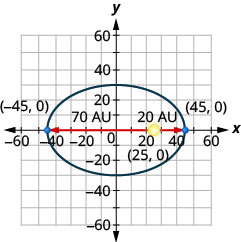
    10. Un cometa se mueve en órbita elíptica alrededor de un sol. Lo más cerca que el cometa llega al sol es aproximadamente\(20\) AU y el más alejado es aproximadamente\(70\) AU. El sol es uno de los focos de la órbita elíptica. Dejando que la elipse se centre en el origen y etiquetando los ejes en AU, la órbita se verá como la figura de abajo. Usa la gráfica para escribir una ecuación para la órbita elíptica del cometa.

    La figura muestra un modelo de una órbita elíptica alrededor del sol en el plano de coordenadas x y. La elipse tiene un centro en (0, 0), un eje mayor horizontal, vértices marcados en (más o menos 45, 0), el sol marcado como focos y etiquetado (25, 0), la distancia más cercana al que está el cometa del sol marcado como 20 A U, y lo más alejado un cometa está del sol marcado como 70 A U.
    Figura 11.E.37

    11. La suma de dos números es\(22\) y el producto es\(−240\). Encuentra los números.

    12. Para su cumpleaños, los abuelos de Olive le compraron un nuevo televisor de pantalla ancha. Antes de abrirlo quiere asegurarse de que se ajuste a su centro de entretenimiento. El televisor es\(55\)”. El tamaño de un televisor se mide en la diagonal de la pantalla y una pantalla ancha tiene una longitud que es mayor que el ancho. La pantalla también tiene un área de pulgadas\(1452\) cuadradas. Su centro de entretenimiento tiene un inserto para el televisor con un largo de\(50\) pulgadas y ancho de\(40\) pulgadas. ¿Cuál es el largo y ancho de la pantalla del televisor y encajará en el centro de entretenimiento de Olive?

    Responder

    2.

    1. Círculo
    2. \((x+5)^{2}+(y+3)^{2}=4\)
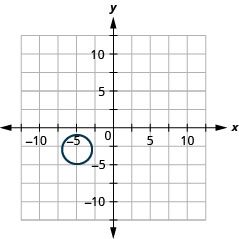
    La figura muestra un círculo graficado en el plano de coordenadas x y. El eje x del plano va de 14 negativo a 14. El eje y del plano va de negativo 10 a 10. El círculo tiene un centro en (negativo 5, negativo 3) y un radio 2.
    Figura 11.E.38

    4.

    1. Hipérbola
    2. \(\frac{(x-2)^{2}}{25}-\frac{(y+1)^{2}}{9}=1\)
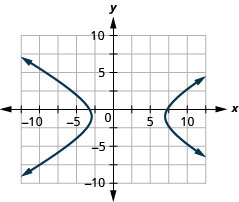
    La figura muestra una hipérbola graficada en el plano de coordenadas x y. El eje x del plano va de 14 negativo a 14. El eje y del plano va de negativo 10 a 10. La hipérbola tiene un centro en (2, negativo 1) y ramas que pasan por los vértices (negativo 3, negativo 1) y (7, negativo 1) que se abren a izquierda y derecha.
    Figura 11.E.39

    6. Sin solución

    8. \((0,-3),(0,3)\)

    10. \(\frac{x^{2}}{2025}+\frac{y^{2}}{1400}=1\)

    12. El largo es\(44\) pulgadas y el ancho es\(33\) pulgadas. El televisor encajará en el centro de entretenimiento de Olive.

    Glosario

    sistema de ecuaciones no lineales
    Un sistema de ecuaciones no lineales es un sistema donde al menos una de las ecuaciones no es lineal.

    This page titled Capítulo 11 Ejercicios de revisión is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform.