4.1: Sistema de Ecuaciones - Gráfica
- Page ID
- 117561
Dadas dos ecuaciones lineales y después de graficar las líneas,
Solución 1. Si las dos líneas se cruzan, entonces el punto de intersección es la solución al sistema, es decir, la solución es un par ordenado\((x, y)\).
Solución 2. Si las dos líneas no se cruzan y son paralelas, es decir, tienen la misma pendiente y diferentes\(y\) -intercepciones, entonces el sistema no tiene solución.
Solución 3. Si las dos líneas son la misma línea, entonces la solución son infinitamente muchas soluciones en esa línea.
Verificación de Soluciones
¿Es el par ordenado\((2, 1)\) una solución para el sistema?\[\left\{\begin{array}{l}3x-y=5 \\ x+y=3\end{array}\right. \quad ?\nonumber\]
Solución
Para verificar si\((2, 1)\) es la solución al sistema, conectamos n-chug\((2, 1)\) en cada ecuación y determinamos si obtenemos una declaración verdadera. Si obtenemos declaraciones verdaderas para ambas ecuaciones en el sistema, entonces\((2, 1)\) será la solución al sistema.
\[\begin{array}{rl}3x-y=5&\text{Plug-n-chug }x=2\text{ and }y=1 \\ 3(\color{blue}{2}\color{black}{})-(\color{blue}{1}\color{black}{})\stackrel{?}{=}5&\text{Simplify} \\ 6-1\stackrel{?}{=}5&\text{Subtract} \\ 5=5&\checkmark\:\text{True}\end{array}\nonumber\]
Hagamos lo mismo para la segunda ecuación:
\[\begin{array}{rl}x+y=3&\text{Plug-n-chug }x=2\text{ and }y=1 \\ (\color{blue}{2}\color{black}{})+(\color{blue}{1}\color{black}{})\stackrel{?}{=}3&\text{Add} \\ 3=3&\checkmark\:\text{True}\end{array}\nonumber\]
Dado que el par ordenado\((2, 1)\) hace que ambas declaraciones sean verdaderas, entonces\((2, 1)\) es una solución para el sistema. De ahí que si tuviéramos que graficar estas líneas, se cruzarían en el punto\((2, 1)\).
¿Es el par ordenado\((−3, −4)\) una solución para el sistema?\[\left\{\begin{array}{l}5x+4y=-31 \\ 3x+6y=-36\end{array}\right.\quad ?\nonumber\]
Solución
Para verificar si\((−3, −4)\) es la solución al sistema, conectamos n-chug\((−3, −4)\) en cada ecuación y determinamos si obtenemos una declaración verdadera. Si obtenemos declaraciones verdaderas para ambas ecuaciones en el sistema, entonces\((−3, −4)\) será la solución al sistema.
\[\begin{array}{rl}5x+4y=-31&\text{Plug-n-chug }x=-3\text{ and }y=-4 \\ 5(\color{blue}{-3}\color{black}{})+4(\color{blue}{-4}\color{black}{})\stackrel{?}{=}-31&\text{Simplify} \\ -15-16\stackrel{?}{=}=31&\text{Subtract} \\ -31=-31&\checkmark\:\text{True}\end{array}\nonumber\]
Hagamos lo mismo para la segunda ecuación:
\[\begin{array}{rl}3x+6y=-36&\text{Plug-n-chug }x=-3\text{ and }y=-4 \\ 3(\color{blue}{-3}\color{black}{})+6(\color{blue}{-4}\color{black}{})\stackrel{?}{=}-36&\text{Simplify} \\ -9-24\stackrel{?}{=}-36&\text{Subtract} \\ -33\neq -36&X \:\text{False}\end{array}\nonumber\]
Dado que el par ordenado\((−3, −4)\) hace que solo una de las afirmaciones sea cierta, entonces no\((−3, −4)\) es una solución para el sistema. Recordemos, el par ordenado debe hacer que la afirmación sea verdadera para ambas ecuaciones a fin de ser una solución al sistema.
Resolver un sistema graficando
Resuelve el sistema graficando:\[\left\{ \begin{array}{l}y=-\dfrac{1}{2}x+3 \\ y=\dfrac{3}{4}x-2\end{array}\right.\nonumber\]
Solución
Primero tenemos que decidir el método en el que vamos a graficar. Aprendimos en el capítulo anterior a hacer una tabla, usar intercepciones o usar la forma pendiente-intercepción. Observe que ambas ecuaciones se dan en forma de pendiente-intersección. Sigamos adelante y usemos la forma pendiente-intercepción para graficar las líneas.
\[\begin{array}{ll}y=-\dfrac{1}{2}x+3&(1) \\ y=\dfrac{3}{4}x-2&(2)\end{array}\nonumber\]
Gráficaremos la línea (1) con una línea continua y la línea gráfica (2) con una línea discontinua.
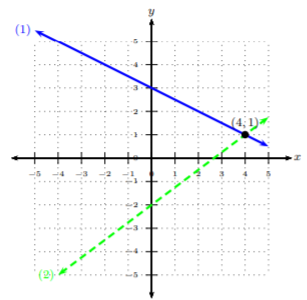
Podemos ver después de graficar las dos líneas que se cruzan en el punto\((4, 1)\). De ahí que la solución al sistema sea\((4, 1)\).
Resuelve el sistema graficando:\[\left\{\begin{array}{l}6x-3y=-9 \\ 2x+2y=-6\end{array}\right.\nonumber\]
Solución
Primero tenemos que decidir el método en el que vamos a graficar. Aprendimos en el capítulo anterior a hacer una tabla, usar intercepciones o usar la forma pendiente-intercepción. Dado que ambas ecuaciones no se dan en forma pendiente-intercepción como en Ejemplo 4.1.3 , podemos reescribirlas en forma pendiente-intercepción, luego graficar. Entonces, reescribamos cada ecuación en forma de pendiente-intercepción:\[\begin{array}{ll}6x-3y=-9 &2x+2y=-6 \\ -3y=-6x-9&2y=-2x-6 \\ y=\dfrac{-6x}{-3}-\dfrac{9}{-3}&y=\dfrac{-2}{2}x-\dfrac{6}{2} \\ y=2x+3&y=-x-3\end{array}\nonumber\]
Sigamos adelante y usemos la forma pendiente-intercepción para graficar las líneas.
\[\begin{array}{ll}y=2x+3&(1) \\ y=-x-3&(2)\end{array}\nonumber\]
Gráficaremos la línea (1) con una línea continua y la línea gráfica (2) con una línea discontinua.
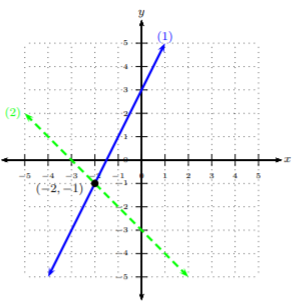
Podemos ver después de graficar las dos líneas que se cruzan en el punto\((−2, −1)\). De ahí que la solución al sistema sea\((−2, −1)\).
Resuelve el sistema graficando:\[\left\{\begin{array}{l}y=\dfrac{3}{2}x-4 \\ y=\dfrac{3}{2}x+1\end{array}\right.\nonumber\]
Solución
Primero tenemos que decidir el método en el que vamos a graficar. Aprendimos en el capítulo anterior a hacer una tabla, usar intercepciones o usar la forma pendiente-intercepción. Observe que ambas ecuaciones se dan en forma de pendiente-intersección. Sigamos adelante y usemos la forma pendiente-intercepción para graficar las líneas.
\[\begin{array}{ll}y=\dfrac{3}{2}x-4&(1) \\ y=\dfrac{3}{2}x+1&(2)\end{array}\nonumber\]
Gráficaremos la línea (1) con una línea continua y la línea gráfica (2) con una línea discontinua.
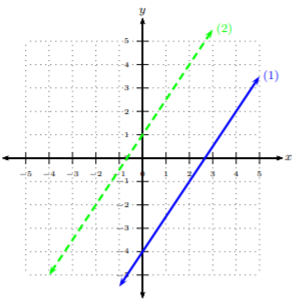
Podemos ver después de graficar las dos líneas que estas dos líneas son paralelas. De ahí que no haya solución al sistema (ya que nunca se cruzarán). Tenga en cuenta, pudimos ver por el sistema que estas líneas compartían la misma pendiente, pero tenían diferentes\(y\) -intercepciones. Sin graficar, podríamos haber visto que estas líneas eran paralelas, de ahí que no tuvieran solución.
Resuelve el sistema graficando:\[\left\{\begin{array}{l}2x-6y=12 \\ 3x-9y=18\end{array}\right.\nonumber\]
Solución
Primero tenemos que decidir el método en el que vamos a graficar. Aprendimos en el capítulo anterior a hacer una tabla, usar intercepciones o usar la forma pendiente-intercepción. Dado que ninguna de las ecuaciones está escrita en forma de pendiente-intersección, intentemos graficar haciendo una tabla para cada ecuación. Comience con la ecuación (1):
\[\begin{array}{lr} x=-3\quad & 2\color{blue}{(-3)}\color{black}{}-6y=12 \\ & -6-6y=12 \\ &-6y=18 \\ & y=-3\end{array}\nonumber\]
\[\begin{array}{lr} x=0\quad & 2\color{blue}{(0)}\color{black}{}-6y=12 \\ &-6y=12 \\ &y=-2\end{array}\nonumber\]
\[\begin{array}{lr} x=3\quad & 2\color{blue}{(3)}\color{black}{}-6y=12 \\ &6-6y=12 \\ &-6y=6 \\ &y=-1 \end{array}\nonumber\]
| \(x\) | \(y\) |
|---|---|
| \ (x\) ">\(-3\) | \ (y\) ">\(-3\) |
| \ (x\) ">\(0\) | \ (y\) ">\(-2\) |
| \ (x\) ">\(3\) | \ (y\) ">\(-1\) |
A continuación, ecuación (2):
\[\begin{array}{lr} x=-3\quad &3\color{blue}{(-3)}\color{black}{}-9y=18 \\ &-9-9y=18 \\ &-9y=27 \\ &y=-3\end{array}\nonumber\]
\[\begin{array}{lr} x=0\quad &3\color{blue}{(0)}\color{black}{}-9y=18 \\ &-9y=18 \\ &y=-2\end{array}\nonumber\]
\[\begin{array}{lr}x=3\quad &3\color{blue}{(3)}\color{black}{}-9y=18 \\ &9-9y=18 \\ &-9y=9 \\ &y=-1\end{array}\nonumber\]
| \(x\) | \(y\) |
|---|---|
| \ (x\) ">\(-3\) | \ (y\) ">\(-3\) |
| \ (x\) ">\(0\) | \ (y\) ">\(-2\) |
| \ (x\) ">\(3\) | \ (y\) ">\(-1\) |
Ahora, vamos a graficar los pares ordenados. Gráficaremos la línea (1) con una línea continua y la línea gráfica (2) con una línea discontinua.
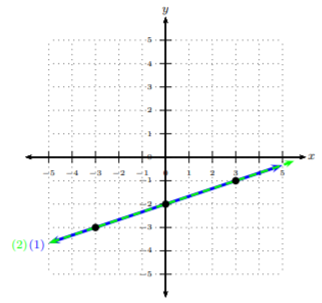
Podemos ver después de graficar las dos líneas que estas dos líneas son iguales. De ahí que haya infinitamente muchas soluciones en la línea\(2x − 6y = 12\) (o la otra ecuación) al sistema (ya que se cruzan en cada punto de la línea). Tenga en cuenta, pudimos ver por el sistema que estas líneas compartían la misma pendiente e\(y\) -intercepta (después de ponerlas en forma de pendiente-intercepción). Sin graficar, podríamos haber visto que estas líneas eran la misma línea, de ahí que tuvieran infinitamente muchas soluciones.
Los babilonios fueron los primeros en trabajar con sistemas de ecuaciones con dos variables. Sin embargo, su trabajo con sistemas fue rápidamente pasado por los griegos, alrededor del 300 d.C., quienes resolverían sistemas de ecuaciones con tres o cuatro variables y eventualmente desarrollaron métodos para resolver sistemas con cualquier número de incógnitas.
Sistemas de Ecuaciones: Graficar la tarea
Determinar si el par (s) ordenado (s) dado (s) es una solución para el sistema.
\(\begin{array}{l}2x+8y=0 \\ -8x+3y=38;\: (-4,1)\end{array}\)
\(\begin{array}{l}-5x+6y=11 \\ 4x+2y=-4;\: (-1,1)\end{array}\)
\(\begin{array}{l}6x+5y=49 \\ -x-6y=-34;\: (4,5)\end{array}\)
\(\begin{array}{l} -2x+2y=-8 \\ -6x-3y=-6;\: (2,-2)\end{array}\)
Resuelve cada sistema graficando.
\(\begin{array}{l}y=-x+1 \\ y=-5x-3\end{array}\)
\(\begin{array}{l}y=-3 \\ y=-x-4\end{array}\)
\(\begin{array}{l}y=-\dfrac{3}{4}x+1 \\ y=-\dfrac{3}{4}x+2\end{array}\)
\(\begin{array}{l}y=\dfrac{1}{3}x+2 \\ y=-\dfrac{5}{3}x-4\end{array}\)
\(\begin{array}{l}y=\dfrac{5}{3}x+4 \\ y=-\dfrac{2}{3}x-3\end{array}\)
\(\begin{array}{l}x+3y=-9 \\ 5x+3y=3\end{array}\)
\(\begin{array}{l}x-y=4 \\ 2x+y=-1\end{array}\)
\(\begin{array}{l}2x+3y=-6 \\ 2x+y=2\end{array}\)
\(\begin{array}{l}2x+y=2 \\ x-y=4\end{array}\)
\(\begin{array}{l}2x+y=-2 \\ x+3y=9\end{array}\)
\(\begin{array}{l}0=-6x-9y+36 \\ 12=6x-3y\end{array}\)
\(\begin{array}{l}2x-y=-1 \\ 0=-2x-y-3\end{array}\)
\(\begin{array}{l}3+y=-x \\ -4-6x=-y\end{array}\)
\(\begin{array}{l}-y+7x=4 \\ -y-3+7x=0\end{array}\)
\(\begin{array}{l}-12+x=4y \\ 12-5x=4y\end{array}\)
\(\begin{array}{l}y=-\dfrac{5}{4}x-2 \\ y=-\dfrac{1}{4}x+2\end{array}\)
\(\begin{array}{l}y=-x-2 \\ y=\dfrac{2}{3}x+3\end{array}\)
\(\begin{array}{l}y=2x+2 \\ y=-x-4\end{array}\)
\(\begin{array}{l}y=2x-4 \\ y=\dfrac{1}{2}x+2\end{array}\)
\(\begin{array}{l}y=\dfrac{1}{2}x+4 \\ y=\dfrac{1}{2}x+1\end{array}\)
\(\begin{array}{l}x+4y=-12 \\ 2x+y=4\end{array}\)
\(\begin{array}{l}6x+y=-3 \\ x+y=2\end{array}\)
\(\begin{array}{l}3x+2y=2 \\ 3x+2y=-6\end{array}\)
\(\begin{array}{l}x+2y=6 \\ 5x-4y=16\end{array}\)
\(\begin{array}{l}x-y=3 \\ 5x+2y=8\end{array}\)
\(\begin{array}{l}-2y+x=4 \\ 2=-x+\dfrac{1}{2}y\end{array}\)
\(\begin{array}{l}-2y=-4-x \\ -2y=-5x+4\end{array}\)
\(\begin{array}{l}16=-x-4y \\ -2x=-4-4y\end{array}\)
\(\begin{array}{l}-4+y=x \\ x+2=-y\end{array}\)
\(\begin{array}{l}-5x+1=-y \\ -y+x=-3\end{array}\)


