4.5: Sistemas de tres ecuaciones lineales en tres variables
- Page ID
- 117571
Resolver sistemas de ecuaciones lineales en tres variables es muy similar a los métodos en los que resolvemos sistemas lineales en dos variables. Con sistemas lineales en dos variables, reducimos el sistema a una ecuación lineal en una variable (por sustitución o adición). Con sistemas lineales en tres variables, aplicamos el mismo método excepto que reducimos el sistema de tres ecuaciones lineales en tres variables a dos ecuaciones lineales en dos variables primero, luego a una ecuación lineal en una variable.
Se da un sistema de tres ecuaciones lineales en tres variables en la forma\[\left\{\begin{array}{ll}ax+by+cz&=d \\ ex+fy+gz&=h \\ ix+jy+kz&=\ell \end{array}\right.\nonumber\] donde\(a,\: b,\: c,\: d,\: e,\: f,\: g,\: h,\: i,\: j,\: k\) y\(\ell\) son coeficientes y\(x,\: y,\) y\(z\) son variables. Este sistema se representa en forma estándar.
Verificación de Soluciones
Como hicimos es la sección anterior para verificar soluciones con dos ecuaciones lineales en dos variables, podemos verificar si un triple ordenado es una solución al sistema de ecuaciones lineales en tres variables.
Determinar si\((5, −3, −4)\) es una solución para el sistema:\[\left\{\begin{array}{l}x+y+z=-2 \\ x+2y-3z=12 \\ 2x-2y+z=-9\end{array}\right.\nonumber\]
Solución
Para verificar si\((5, −3, −4)\) es la solución al sistema, conectamos n-chug\((5, −3, −4)\) en cada ecuación y determinamos si obtenemos una declaración verdadera. Si obtenemos declaraciones verdaderas para todas las ecuaciones en el sistema, entonces\((5, −3, −4)\) será la solución al sistema.
\[\begin{array}{rl}x+y+z=-2 &\text{Plug-n-chug }x=5,\: y=-3\text{ and }z=-4 \\ \color{blue}{5}\color{black}{}+(\color{blue}{-3}\color{black}{})+(\color{blue}{-4}\color{black}{})\stackrel{?}{=}-2&\text{Simplify} \\ 5-3-4\stackrel{?}{=}-2&\text{Subtract} \\ -2=-2&\checkmark\text{ True}\end{array}\nonumber\]
Hagamos lo mismo para la segunda ecuación:
\[\begin{array}{rl}x+2y-3z=12&\text{Plug-n-chug }x=5,\: y=-3\text{ and }z=-4 \\ \color{blue}{5}\color{black}{}+2(\color{blue}{-3}\color{black}{})-3(\color{blue}{-4}\color{black}{})\stackrel{?}{=}12&\text{Simplify} \\ 11=12&X\text{ False}\end{array}\nonumber\]
Dado que el triple ordenado\((5, −3, −4)\) hace falsa la segunda ecuación, entonces no\((5, −3, −4)\) es la solución al sistema.
Vamos a probar un triple ordenado diferente. Determinar si\((−1, 2, −3)\) es una solución para el sistema:\[\left\{\begin{array}{l}x+y+z=-2 \\ x+2y-3z=12 \\ 2x-2y+z=-9\end{array}\right.\nonumber\]
Solución
Para verificar si\((−1, 2, −3)\) es la solución al sistema, conectamos n-chug\((−1, 2, −3)\) en cada ecuación y determinamos si obtenemos una declaración verdadera. Si obtenemos declaraciones verdaderas para todas las ecuaciones en el sistema, entonces\((−1, 2, −3)\) será la solución al sistema.
\[\begin{array}{rl}x+y+z=-2 &\text{Plug-n-chug }x=-1,\: y=2\text{ and }z=-3 \\ \color{blue}{-1}\color{black}{}+\color{blue}{2}\color{black}{}+(\color{blue}{-3}\color{black}{})\stackrel{?}{=}-2&\text{Simplify} \\ -2=-2&\checkmark\text{ True}\end{array}\nonumber\]
Hagamos lo mismo para la segunda ecuación:
\[\begin{array}{rl}x+2y-3z=12&\text{Plug-n-chug }x=-1,\: y=2\text{ and }z=-3 \\ \color{blue}{-1}\color{black}{}+2(\color{blue}{2}\color{black}{})-3(\color{blue}{-3}\color{black}{})\stackrel{?}{=}12&\text{Simplify} \\ 12=12&\checkmark\text{ True}\end{array}\nonumber\]
Hagamos lo mismo para la tercera ecuación:
\[\begin{array}{rl}2x-2y+z=-9&\text{Plug-n-chug }x=-1,\: y=2\text{ and }z=-3 \\ 2(\color{blue}{-1}\color{black}{})-2(\color{blue}{2}\color{black}{})+(\color{blue}{-3}\color{black}{})\stackrel{?}{=}-9&\text{Simplify} \\ -9=-9&\checkmark\text{ True}\end{array}\nonumber\]
Dado que el triple ordenado\((−1, 2, −3)\) hace verdaderas todas las ecuaciones en el sistema, entonces\((−1, 2, −3)\) es una solución al sistema.
Resolver sistemas de tres ecuaciones lineales en tres variables
En Ejemplo 4.5.2 , determinamos que la calla ordenada\((-1, 2, -3)\) es una solución para el sistema
\[\left\{\begin{array}{l}x+y+z=-2 \\ x+2y-3z=12 \\ 2x-2y+z=-9\end{array}\right.\nonumber\]
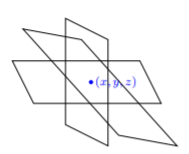
¿Qué significa esto? Con sistemas de dos ecuaciones lineales en dos variables, sabemos que si el sistema es consistente con una solución independiente, entonces la solución es un par ordenado y dos líneas se cruzan. Sin embargo, con tres ecuaciones lineales en tres variables, ¿cómo es un sistema consistente con una solución independiente? Sabemos que la respuesta es un triple ordenado de forma\((x, y, z)\), pero ¿cómo se ve la gráfica? Bueno, vamos a echar un vistazo.
Si obtenemos un sistema consistente con una solución independiente, entonces la solución es un triple ordenado. Este triple ordenado único representa la intersección de tres planos.
No obstante, la experiencia de las secciones anteriores nos dice que no siempre es así, ¿verdad? Con dos ecuaciones lineales en dos variables, tenemos dos casos especiales: sin solución e infinitamente muchas soluciones en línea\(y = mx + b\).
Recordar. Ninguna solución significó que las dos líneas fueran paralelas y nunca se cruzaban. Infinitamente muchas soluciones en línea\(y = mx + b\) significaron que las dos líneas eran, de hecho, la misma línea\(y = mx + b\).
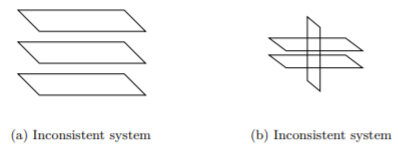
Echemos un vistazo a dos casos con sistemas que son inconsistentes, pero ahora con tres ecuaciones lineales en tres variables y con planos.
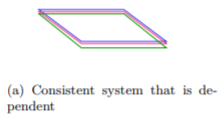
Por último, echemos un vistazo a un caso con un sistema consistente que es dependiente, pero ahora con tres ecuaciones lineales en tres variables y con planos.
Resuelve el sistema:\[\left\{\begin{array}{l}3x+2y-z=-1 \\ -2x-2y+3z=5 \\ 5x+2y-z=3\end{array}\right.\nonumber\]
Solución
Sigamos adelante y numeremos cada ecuación para que podamos identificar cada ecuación.
\[\begin{align}3x+2y-z=-1& \tag{1} \\ -2x-2y+3z=5 &\tag{2} \\ 5x+2y-z=3 &\tag{3} \end{align}\]
Primero, elegimos una variable para eliminar. Luego toma dos ecuaciones, digamos (1) y (2), y elimina la variable elegida. Vamos a elegir\(y\) ya que podemos ver que los coeficientes de\(y\) son los mismos y podemos eliminarlo fácilmente.
\[\begin{align} 3x+2y-z=-1& \tag{1} \\ -2x-2y+3z=5& \tag{2}\end{align}\]
Añadiendo (1) y (2), obtenemos
\[\begin{align} x+2z=4& \tag{4}\end{align}\]
Ahora, tomemos las ecuaciones (2) y (3) y eliminemos de\(y\) nuevo:
\[\begin{align} -2x-2y+3z=5 &\tag{2} \\ 5x+2y-z=3 &\tag{3} \end{align}\]
Añadiendo (2) y (3), obtenemos
\[\begin{align} 3x+2z=8& \tag{5}\end{align}\]
A continuación, tome las ecuaciones (4) y (5). Observe, tenemos un sistema de dos ecuaciones lineales en dos variables:
\[\begin{align} x+2z=4& \tag{4} \\ 3x+2z=8&\tag{5}\end{align}\]
Utilizamos el mismo proceso que hicimos en la sección anterior para obtener la solución para\(x\) y\(z\). Después sustituya esos valores en una de las ecuaciones originales para obtener\(y\). Así, obteniendo la triple solución ordenada.
Optemos por eliminar\(z\) y resolver para\(x\). Primero, multipliquemos la ecuación (4) por\(−1\).
\[\begin{align} \color{blue}{-1}\color{black}{}(x+2z)&=\color{blue}{-1}\color{black}{}(4) \tag{4} \\ 3x+2z&=8 \tag{5}\end{align}\]
Ahora, podemos resolver para\(x\):
\[\begin{align} -x-2z&=-4 \tag{4} \\ 3x+2z&=8\tag{5}\end{align}\]
Sumando estos juntos, obtenemos
\[\begin{aligned}2x&=4 \\ x&=2\end{aligned}\]
Si\(x = 2\), entonces esto implica que\(z = 1\), es decir,
\[\begin{align} x+2z&=4 \tag{4} \\ \color{blue}{2}\color{black}{}+2z&=4\nonumber \\ 2z&=2\nonumber \\ z&=1\nonumber \end{align}\]
Por último, tomamos\(x = 2\)\(z = 1\) y las sustituimos en una de las ecuaciones originales, como (1), y resolvemos por\(y\):
\[\begin{align} 3x+2y-z&=-1 \tag{1} \\ 3\color{blue}{(2)}\color{black}{}+2y-\color{blue}{(1)}\color{black}{}&=-1\nonumber \\ 6+2y-1&=-1\nonumber \\ 5+2y&=-1\nonumber \\ 2y&=-6\nonumber \\ y&=-3\nonumber \end{align}\]
Así, el punto de intersección de los tres planos es el triple ordenado\((2, −3, 1)\).
Alrededor del 250 a. C., se publicaron en China Los nueve capítulos sobre el arte matemático. Este libro tenía 246 problemas, y el Capítulo 8 trataba de resolver sistemas de ecuaciones. ¡Un problema tenía cuatro ecuaciones con cinco variables!
Casos Especiales
Mirando hacia atrás en la Figura 1.2, vemos que hay dos casos especiales: Sistemas inconsistentes y sistemas consistentes con soluciones dependientes. Veamos ejemplos de estos casos especiales.
Resuelve el sistema:\[\left\{\begin{array}{l}5x-4y+3z=-4 \\ -10x+8y-6z=8 \\ 15x-12y+9z=-12\end{array}\right.\nonumber\]
Solución
Sigamos adelante y numeremos cada ecuación para que podamos identificar cada ecuación.
\[\begin{align}5x-4y+3z&=-4 \tag{1} \\ -10x+8y-6z&=8 \tag{2} \\ 15x-12y+9z&=-12 \tag{3}\end{align}\]
Primero, elegimos una variable para eliminar. Luego toma dos ecuaciones, digamos (1) y (2), y elimina la variable elegida. Vamos a elegir\(z\) ya que podemos ver que los coeficientes de\(z\) son casi los mismos y podemos eliminarlo fácilmente. Primero multiplicamos la ecuación (1) por\(2\) y luego sumamos.
\[\begin{align}\color{blue}{2}\color{black}{}(5x-4y+3z)&=\color{blue}{2}\color{black}{}(-4)\tag{1} \\ -10x+8y-6z&=8\tag{2}\end{align}\]
Ahora, podemos agregar para eliminar\(z\):
\[\begin{align}10x-8y+6z&=-8 \tag{1} \\ -10x+8y-6z&=8\tag{2} \end{align}\]
Añadiendo (1) y (2), obtenemos
\[0=0\quad\checkmark\text{ True}\nonumber\]
Dado que todas las variables eliminan y nos queda una afirmación verdadera, sabemos que este es un sistema consistente con soluciones dependientes. Sin embargo, ¿cuál es la solución? Vemos en la Figura 4.5.3 a que esto significa que los tres planos son el mismo plano. De ahí que debamos escribir la solución como\(\{(x, y, z)|5x − 4y + 3z = −4\}\).
Resuelve el sistema:\[\left\{\begin{array}{l}3x-4y+z=2 \\ -9x+12y-3z=-5 \\ 4x-2y-z=3\end{array}\right.\nonumber\]
Solución
Sigamos adelante y numeremos cada ecuación para que podamos identificar cada ecuación.
\[\begin{align} 3x-4y+z=2&\tag{1} \\ -9x+12y-3z=-5&\tag{2} \\ 4x-2y-z=3&\tag{3}\end{align}\]
Primero, elegimos una variable para eliminar. Luego toma dos ecuaciones, digamos (1) y (2), y elimina la variable elegida. Vamos a elegir\(x\) ya que podemos ver que los coeficientes de\(x\) son casi los mismos y podemos eliminarlo fácilmente. Primero multiplicamos la ecuación (1) por\(3\) y luego sumamos.
\[\begin{align}\color{blue}{3}\color{black}{}(3x-4y+z)&=\color{blue}{3}\color{black}{}(2) \tag{1} \\ -9x+12y-3z&=-5\tag{2}\end{align}\]
Ahora, podemos agregar para eliminar\(z\):
\[\begin{align}9x-12y+3z&=6\tag{1} \\ -9x+12y-3z&=-5\tag{2}\end{align}\]
Añadiendo (1) y (2), obtenemos
\[0=1\quad X\text{ False}\nonumber\]
Ya que todas las variables eliminan y nos quedamos con una declaración falsa, sabemos que este es un sistema inconsistente y no hay solución.
Los sistemas de ecuaciones en tres (o más) variables no son más difíciles que los sistemas de ecuaciones en dos variables siempre y cuando tengamos cuidado de mantenernos organizados. Es posible resolver cada sistema de varias maneras diferentes. Podemos usar diferentes pares de ecuaciones o eliminar variables en un orden diferente. En un futuro capítulo, ¡tenemos la oportunidad de resolver sistemas de ecuaciones no lineales!
Sistemas de Tres Ecuaciones Lineales en Tres Variables Tarea
Resuelve cada sistema. Determinar si cada sistema es consistente, independiente o dependiente, o inconsistente. Escribe la solución como un triple ordenado, si es posible.
\(\begin{array}{l} a − 2b + c = 5\\ 2a + b − c = −1 \\ 3a + 3b − 2c = −4\end{array}\)
\(\begin{array}{l} 3x + y − z = 11 \\ x + 3y = z + 13 \\ x + y − 3z = 11 \end{array}\)
\(\begin{array}{l} x + 6y + 3z = 4 \\ 2x + y + 2z = 3 \\ 3x − 2y + z = 0 \end{array}\)
\(\begin{array}{l} x + y + z = 6 \\ 2x − y − z = −3 \\ x − 2y + 3z = 6 \end{array}\)
\(\begin{array}{l} x + y − z = 0 \\ x − y − z = 0 \\ x + y + 2z = 0 \end{array}\)
\(\begin{array}{l} −2x + y − 3z = 1 \\ x − 4y + z = 6 \\ 4x + 16y + 4z = 24 \end{array}\)
\(\begin{array}{l} 2x + y − 3z = 0 \\ x − 4y + z = 0 \\ 4x + 16y + 4z = 0 \end{array}\)
\(\begin{array}{l} 3x + 2y + 2z = 3 \\ x + 2y − z = 5 \\ 2x − 4y + z = 0 \end{array}\)
\(\begin{array}{l} x − 2y + 3z = 4 \\ 2x − y + z = −1 \\ 4x + y + z = 1 \end{array}\)
\(\begin{array}{l} x − y + 2z = 0 \\ x − 2y + 3z = −1 \\ 2x − 2y + z = −3 \end{array}\)
\(\begin{array}{l} 4x − 3y + 2z = 40 \\ 5x + 9y − 7z = 47 \\ 9x + 8y − 3z = 97 \end{array}\)
\(\begin{array}{l} 2x + 3y = z − 1 \\ 3x = 8z − 1 \\ 5y + 7z = −1 \end{array}\)
\(\begin{array}{l} x + y + z = 2 \\ 6x − 4y + 5z = 31 \\ 5x + 2y + 2z = 13 \end{array}\)
\(\begin{array}{l} x − y + 2z = −3 \\ x + 2y + 3z = 4 \\ 2x + y + z = −3 \end{array}\)
\(\begin{array}{l} x + y − z = 0 \\ x + 2y − 4z = 0 \\ 2x + y + z = 0 \end{array}\)
\(\begin{array}{l} x + 2y − z = 4 \\ 4x − 3y + z = 8 \\ 5x − y = 12 \end{array}\)
\(\begin{array}{l} 4x + 12y + 16z = 4 \\ 3x + 4y + 5z = 3 \\ x + 8y + 11z = 1 \end{array}\)
\(\begin{array}{l} 4x + 12y + 16z = 0 \\ 3x + 4y + 5z = 0 \\ x + 8y + 11z = 0 \end{array}\)
\(\begin{array}{l} p + q + r = 1 \\ p + 2q + 3r = 4 \\ 4p + 5q + 6r = 7 \end{array}\)
\(\begin{array}{l} x + 2y − 3z = 9 \\ 2x − y + 2z = −8 \\ 3x − y − 4z = 3 \end{array}\)
\(\begin{array}{l} 4x − 7y + 3z = 1 \\ 3x + y − 2z = 4 \\ 4x − 7y + 3z = 6 \end{array}\)
\(\begin{array}{l} 3x + y − z = 10 \\ 8x − y − 6z = −3 \\ 5x − 2y − 5z = 1 \end{array}\)
\(\begin{array}{l} 3x + 3y − 2z = 13 \\ 6x + 2y − 5z = 13 \\ 5x − 2y − 5z = −1 \end{array}\)
\(\begin{array}{l} 3x − 4y + 2z = 1 \\ 2x + 3y − 3z = −1 \\ x + 10y − 8z = 7 \end{array}\)
\(\begin{array}{l} m + 6n + 3p = 8 \\ 3m + 4n = −3 \\ 5m + 7n = 1 \end{array}\)
\(\begin{array}{l} 2x − 3y + 5z = 1 \\ 3x + 2y − z = 4 \\ 4x + 7y − 7z = 7 \end{array}\)
\(\begin{array}{l} 2x + y = z \\ 4x + z = 4y \\ y = x + 1 \end{array}\)
\(\begin{array}{l} 3x + 2y = z + 2 \\ y = 1 − 2x \\ 3z = −2y \end{array}\)
\(\begin{array}{l} −2w + 2x + 2y − 2z = −10 \\ w + x + y + z = −5 \\ 3w + 2x + 2y + 4z = −11 \\ w + 3x − 2y + 2z = −6 \end{array}\)
\(\begin{array}{l} w + x + y + z = 2 \\ w + 2x + 2y + 4z = 1 \\ −w + x − y − z = −6 \\ −w + 3x + y − z = −2 \end{array}\)
\(\begin{array}{l} −w + 2x − 3y + z = −8 \\ −w + x + y − z = −4 \\ w + x + y + z = 22 \\ −w + x − y − z = −14 \end{array}\)
\(\begin{array}{l} w + x − y + z = 0 \\ −w + 2x + 2y + z = 5 \\ −w + 3x + y − z = −4 \\ −2w + x + y − 3z = −7 \end{array}\)


