4.6: Sistemas de dos desigualdades lineales en dos variables
- Page ID
- 117580
En una sección anterior, discutimos las desigualdades lineales en dos variables, donde tenemos la línea límite, discontinua o sólida, y el sombreado ya sea por encima o por debajo\(y\) de la intersección, dependiendo del símbolo de desigualdad. Por ejemplo, recordemos\(y > x + 4\) y su gráfica.
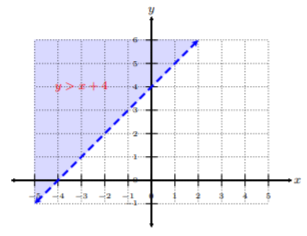
Bueno, usemos esta misma idea para encontrar la solución a un sistema de dos desigualdades lineales en dos variables. El proceso es similar, salvo por el hecho de que la solución, en este caso, es la región con sombreado solapado. Podemos presentar la solución como una región sombreada.
Un sistema de dos desigualdades lineales en dos variables es un sistema de la forma\[\left\{\begin{array}{ll}ax+by &<c \\ dx+ey &f\end{array}\right.\nonumber\] donde\(a,\: b,\: c,\: d,\: e,\) y\(f\) son coeficientes,\(x\) y\(y\) son variables, y la forma es la misma para cualquier combinación de\(>,\: ≤,\: ≥\). Este sistema se representa en forma estándar.
Verificación de Soluciones
Determine si los pares ordenados son una solución para el sistema:\[\left\{\begin{array}{l}x+4y\geq 10 \\ 3x-2y <12 \end{array}\right.\nonumber\]
- \((-2,4)\)
- \((3,1)\)
Solución
Sustituimos los pares ordenados en las desigualdades y determinamos si los resultados son ciertos para ambas desigualdades.
- Sustituyamos\((-2,4)\) en las desigualdades y determinemos si el par ordenado es una solución a ambas desigualdades.
\[\begin{array}{rl} x+4y\stackrel{?}{\geq} 10&\text{Substitute }x=-2\text{ and }y=4 \\ -2+4\color{blue}{(4)}\color{black}{}\stackrel{?}{\geq}10&\text{Simplify} \\ 14\geq 10&\checkmark\text{ True}\end{array}\nonumber\]
\[\begin{array}{rl}3x-2y\stackrel{?}{<}12 &\text{Substitute }x=-2\text{ and }y=4 \\ 3\color{blue}{(-2)}\color{black}{}-2\color{blue}{(4)}\color{black}{}\stackrel{?}{<}&\text{Simplify} \\ -14<12&\checkmark\text{ True}\end{array}\nonumber\]
De ahí,\((-2,4)\) es una solución al sistema. - Sustituyamos\((3, 1)\) en la desigualdad y determinemos si el par ordenado es una solución a ambas desigualdades.
\[\begin{array}{rl}x+4y\stackrel{?}{\geq}10&\text{Substitute }x=3\text{ and }y=1 \\ 3+4\color{blue}{(1)}\color{black}{}\stackrel{?}{\geq}10&\text{Simplify} \\ 7\cancel{\geq}10& X\text{ False}\end{array}\nonumber\]De ahí\((3, 1)\) que no sea una solución al sistema ya que no\((3, 1)\) es una solución a la primera desigualdad\(x + 4y ≥ 10\).
Resolver un sistema de dos desigualdades lineales en dos variables mediante gráficos
En esta sección, resolvemos un sistema de dos desigualdades lineales en dos variables mediante la representación gráfica. Como podemos ver en los pasos dados, el proceso es similar a cuando graficamos desigualdades lineales en dos variables.
Tenemos que preguntarnos: “¿Qué es una solución a un sistema de dos desigualdades lineales en dos variables?” Recordemos, en secciones anteriores de este capítulo, dijimos que la solución a un sistema consistente que es independiente era un punto de intersección. El punto de intersección todavía juega un papel con estos sistemas, pero no estamos buscando un punto. Necesitamos todos los puntos en un área común sombreada que hagan verdaderas ambas desigualdades en el sistema. El punto de intersección es la esquina de esta región sombreada común.
Dado un sistema de dos desigualdades lineales en dos variables,\[\left\{\begin{array}{ll} ax+by &<c \\ dx+ey &<f\end{array}\right. ,\nonumber\] utilizamos los siguientes pasos para graficar el sistema, donde se aplica el mismo proceso para cualquier combinación de\(>,\: ≤,\: ≥\).
Paso 1. Reescribir las desigualdades en forma de pendiente-intersección, es decir,\(y = mx + b\).
Paso 2. Grafique las líneas límite de acuerdo a los dos casos:
Caso 1. Si la desigualdad es\(<\) o\(>\), entonces la línea límite es discontinua.
Caso 2. Si la desigualdad es\(≥\) o\(≤\), entonces la línea límite es sólida.
Paso 3. Sombrear las regiones apropiadas para cada desigualdad lineal.
Paso 4. La solución es la región donde se superpone el sombreado.
Paso 5. Verifique la solución tomando un punto de prueba donde el sombreado se superponga que no esté en las líneas de límite. Pregunta: ¿Este par ordenado hace que ambas desigualdades sean ciertas?
Resuelve el sistema graficando:\[\left\{\begin{array}{l}3x-2y\leq 6 \\ y>-\frac{1}{4}x+5\end{array}\right.\nonumber\]
Solución
Sigamos los pasos dados anteriormente para graficar el sistema de desigualdades lineales en dos variables.
Paso 1. Reescribir las desigualdades en forma de pendiente-intersección, es decir,\(y = mx + b\). \[\begin{aligned} 3x-2y&\leq 6 \\ -2y&\leq -3x+6 \\ y&\leq \frac{3}{2}x-3\end{aligned}\]La segunda desigualdad ya está en forma de pendiente-intercepción, es decir,\(y > −\frac{1}{4}x + 5\).
Paso 2. Grafique las líneas límite de acuerdo a los dos casos. Ya que tenemos\(≥\) y\(>\), entonces tenemos ambos casos donde tenemos una línea sólida con\(≥\) y una línea discontinua con\(>\).
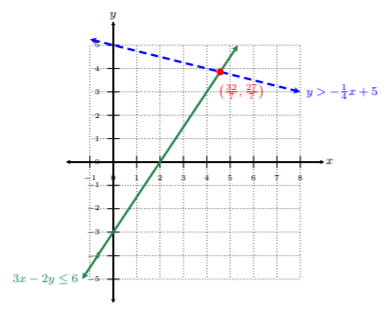
Paso 3. Sombrear las regiones apropiadas para cada desigualdad lineal.
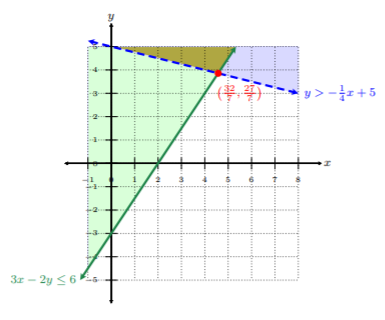
Paso 4. La solución es la región donde se superpone el sombreado.
La región donde se superpone el sombreado es la región oscurecida en la figura anterior (o verde oliva). Observe el punto de intersección en\(\left(\frac{32}{7},\frac{27}{7}\right)\). El punto de intersección sigue siendo crítico para encontrar la solución a este tipo de sistemas.
Paso 5. Verifique la solución tomando un punto de prueba donde el sombreado se superponga que no esté en las líneas de límite. ¡Escojamos el punto de prueba\(\color{blue}{(4, 5)}\) ya que es una gran elección! \[\begin{aligned}3x-2y&\stackrel{?}{\leq}6 \\ 3\color{blue}{(4)}\color{black}{}-2\color{blue}{(5)}\color{black}{}&\stackrel{?}{\leq}6 \\ 2&\leq 6\quad\checkmark\text{True}\end{aligned}\]
\[\begin{aligned} y&\stackrel{?}{>}-\frac{1}{4}x+5 \\ \color{blue}{5}\color{black}{}&\stackrel{?}{>}-\frac{1}{4}\color{blue}{(4)}\color{black}{}+5 \\ 5&>4\quad\checkmark\text{ True}\end{aligned}\]De ahí\((4,5)\) que ambas desigualdades sean verdaderas.
Así, la región oscurecida (o verde oliva) es la solución.
Sistemas de Dos Desigualdades Lineales en Dos Variables Tarea
Determinar si los pares ordenados dados son soluciones al sistema dado.
\(\begin{array}{l} y<\frac{1}{4}x+2 \\ y\geq -4x+1 \\ (6,2),\: (-4,2),\: (9,1) \end{array}\)
\(\begin{array}{l} y\leq x+1 \\ y>-\frac{1}{4}x-2 \\ (-5,1),\: (10,1),\: (4,-2) \end{array}\)
\(\begin{array}{l} y<2x-1 \\ y\geq -x-2 \\ (2,-1),\: (-1,-1),\: (-5,-2) \end{array}\)
Resuelve cada sistema graficando.
\(\begin{array}{l} y>\frac{1}{4}x-1 \\ y<-\frac{1}{2}x+1 \end{array}\)
\(\begin{array}{l} y<2x+1 \\ y>-\frac{1}{2}x+2 \end{array}\)
\(\begin{array}{l} y<4x-2 \\ y>-2x-1 \end{array}\)
\(\begin{array}{l} y>\frac{1}{2}x-2 \\ y<-\frac{1}{4}x+2 \end{array}\)
\(\begin{array}{l} x\leq 6 \\ y<4 \end{array}\)
\(\begin{array}{l} x>-2 \\ y>4 \end{array}\)
\(\begin{array}{l} x\leq 3 \\ y>-2x+5 \end{array}\)
\(\begin{array}{l} x\leq 2 \\ y>-4x+5 \end{array}\)
\(\begin{array}{l} y<2x+2 \\ y>-4x-1 \end{array}\)
\(\begin{array}{l} y>2x-2 \\ y<-x+2 \end{array}\)
\(\begin{array}{l} 2x+y\geq 6 \\ 2x+5y\leq 10 \end{array}\)
\(\begin{array}{l} -2x-y\geq 6 \\ -2x-3y\leq 6 \end{array}\)
\(\begin{array}{l} -2x+y\geq -6 \\ -2x+5y\leq -10 \end{array}\)
\(\begin{array}{l} 2x-y\leq -4 \\ -x+5y\geq -5 \end{array}\)


