5.4: Biblioteca de funciones

Conocer gráficas de funciones comunes ayudan al alumno a visualizar la función y conectar la relación entre la ecuación y su gráfica.

Biblioteca de Funciones

La biblioteca de funciones es un conjunto de funciones que distingue la relación entre las funciones y sus gráficas que incluye el dominio para cada función.

La biblioteca de funciones crece a medida que nos familiarizamos con diferentes tipos de funciones. A medida que tomamos matemáticas de nivel más alto, la biblioteca crece hasta ser muy grande, pero para esta sección, comenzamos con una biblioteca que contiene seis funciones básicas importantes: línea, parábola, cúbica, valor absoluto, racional, raíz cuadrada.

Nota

Las gráficas de las funciones en la biblioteca de funciones son las gráficas generales de las funciones, no las gráficas particulares de funciones. Por lo tanto, podemos usar trazado de puntos, tecnología o transformaciones para graficar funciones particulares, pero tendemos a memorizar la forma general ya que es útil en matemáticas de nivel superior recordar la biblioteca de funciones rápidamente.

Ejemplo 5.4.1

Graficar\(f(x) = x\)\(g(x) = 2\),,\(h(x) = −3x + 1\) y determinar su dominio.

Solución

Observe que las tres funciones son funciones lineales. Podemos trazarlos fácilmente en la misma cuadrícula. Podemos ver que todas las gráficas son líneas y como no hay restricciones a ninguna de las líneas, el dominio es todo números reales o\((−∞, ∞)\). Ya que\(f\) es una línea a través del origen (\(y\)-intercept es cero), y cada\(x\) coordenada es la misma que su\(y\) coordenada correspondiente, e.g.,\((0, 0),\: (1, 1),\) etc., entonces llamamos a\(f\) la función de identidad.

Figura 5.4.1

Ya que\(g\) es una línea horizontal, las\(y\) coordenadas nunca cambian, y no hay un cambio en la pendiente, es decir, la pendiente es cero, entonces llamamos a\(g\) la función constante.

La función\(h\) es una ecuación de una línea con una pendiente distinta de cero y una\(y\) intercepción distinta de cero, y llamamos\(h\) una función lineal.

Ejemplo 5.4.2

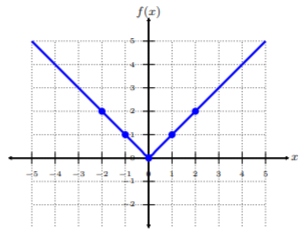
Grafica\(f(x) = |x|\) y determina el dominio.

Solución

Escojamos cinco\(x\) coordenadas y busquemos\(y\) los valores correspondientes. Cada\(x\) -valor es positivo o negativo, y cero. Esta es una práctica común, pero no requerida.

Tabla 5.4.1

\(x\)	\(f(x)=|x|\)	\((x,f(x))\)
\ (x\) ">\(-2\)	\ (f (x) =|x|\) ">\(f(\color{blue}{-2}\color{black}{})=2\)	\ ((x, f (x))\) ">\((-2,2)\)
\ (x\) ">\(-1\)	\ (f (x) =|x|\) ">\(f(\color{blue}{-1}\color{black}{})=1\)	\ ((x, f (x))\) ">\((-1,1)\)
\ (x\) ">\(0\)	\ (f (x) =|x|\) ">\(f(\color{blue}{0}\color{black}{})=0\)	\ ((x, f (x))\) ">\((0,0)\)
\ (x\) ">\(1\)	\ (f (x) =|x|\) ">\(f(\color{blue}{1}\color{black}{})=1\)	\ ((x, f (x))\) ">\((1,1)\)
\ (x\) ">\(2\)	\ (f (x) =|x|\) ">\(f(\color{blue}{2}\color{black}{})=2\)	\ ((x, f (x))\) ">\((2,2)\)

Trazar los cinco pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Esta gráfica parece dos líneas de pendientes opuestas que se encuentran en el origen. De ahí que su gráfica sea dos líneas que se encuentran en el origen, pero se detienen donde se reúne para hacer una forma de v llamada función de valor absoluto Ya que vemos que no hay restricciones a la gráfica, el dominio es todo números reales o\((−∞, ∞)\).

Figura 5.4.2

Ejemplo 5.4.3

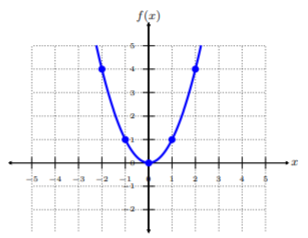
Grafica\(f(x) = x^2\) y determina el dominio.

Solución

Escojamos cinco\(x\) coordenadas y busquemos\(y\) los valores correspondientes. Cada\(x\) valor es positivo, negativo y cero. Esta es una práctica común, pero no requerida.

Tabla 5.4.2

\(x\)	\(f(x)=x^2\)	\((x,f(x)\)
\ (x\) ">\(-2\)	\ (f (x) =x^2\) ">\(f(\color{blue}{-2}\color{black}{})=4\)	\ ((x, f (x)\) ">\((-2,4)\)
\ (x\) ">\(-1\)	\ (f (x) =x^2\) ">\(f(\color{blue}{-1}\color{black}{})=1\)	\ ((x, f (x)\) ">\((-1,1)\)
\ (x\) ">\(0\)	\ (f (x) =x^2\) ">\(f(\color{blue}{0}\color{black}{})=0\)	\ ((x, f (x)\) ">\((0,0)\)
\ (x\) ">\(1\)	\ (f (x) =x^2\) ">\(f(\color{blue}{1}\color{black}{})=1\)	\ ((x, f (x)\) ">\((1,1)\)
\ (x\) ">\(2\)	\ (f (x) =x^2\) ">\(f(\color{blue}{2}\color{black}{})=4\)	\ ((x, f (x)\) ">\((2,4)\)

Trazar los cinco pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Esta gráfica se llama parábola y como esta función es bastante común para la\(x^2\) forma -form, la llamamos función cuadrática (cuadrada). Como vemos no hay restricciones a la gráfica, el dominio es todo números reales o\((−∞, ∞)\).

Figura 5.4.3

Ejemplo 5.4.4

Grafica\(f(x) = x^3\) y determina el dominio.

Solución

Escojamos tres\(x\) coordenadas y busquemos\(y\) los valores correspondientes. Cada\(x\) valor es positivo, negativo y cero. Esta es una práctica común, pero no requerida.

Tabla 5.4.3

\(x\)	\(f(x)=x^3\)	\((x,f(x))\)
\ (x\) ">\(-1\)	\ (f (x) =x^3\) ">\(f(\color{blue}{-1}\color{black}{})=-1\)	\ ((x, f (x))\) ">\((-1,-1)\)
\ (x\) ">\(0\)	\ (f (x) =x^3\) ">\(f(\color{blue}{0}\color{black}{})=0\)	\ ((x, f (x))\) ">\((0,0)\)
\ (x\) ">\(1\)	\ (f (x) =x^3\) ">\(f(\color{blue}{1}\color{black}{})=1\)	\ ((x, f (x))\) ">\((1,1)\)

Trazar los pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Dado que esta función es bastante común para el\(x^3\) -form, la llamamos función cube (cubic). Como vemos no hay restricciones a la gráfica, el dominio es todo números reales o\((−∞, ∞)\).

Figura 5.4.4

Ejemplo 5.4.5

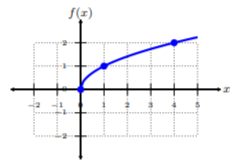
Grafica\(f(x) =\sqrt{x}\) y determina el dominio.

Solución

Escojamos tres\(x\) coordenadas y busquemos\(y\) los valores correspondientes.

Tabla 5.4.4

\(x\)	\(f(x)=\sqrt{x}\)	\((x,f(x))\)
\ (x\) ">\(0\)	\ (f (x) =\ sqrt {x}\) ">\(f(\color{blue}{0}\color{black}{})=0\)	\ ((x, f (x))\) ">\((0,0)\)
\ (x\) ">\(1\)	\ (f (x) =\ sqrt {x}\) ">\(f(\color{blue}{1}\color{black}{})=1\)	\ ((x, f (x))\) ">\((1,1)\)
\ (x\) ">\(4\)	\ (f (x) =\ sqrt {x}\) ">\(f(\color{blue}{4}\color{black}{})=2\)	\ ((x, f (x))\) ">\((4,2)\)

Trazar los pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Dado que esta función es bastante común para el\(\sqrt{x}\) -form, la llamamos función de raíz cuadrada. Como vemos hay una restricción a la gráfica, donde los\(x\) valores comienzan en el origen y ninguna parte de la gráfica está en el lado izquierdo del origen, el dominio de esta función es\(\{x|x ≥ 0\}\) o\([0, ∞)\).

Figura 5.4.5

Ejemplo 5.4.6

Grafica\(f(x) =\sqrt[3]{x}\) y determina el dominio.

Solución

Escojamos tres\(x\) coordenadas y busquemos\(y\) los valores correspondientes.

Tabla 5.4.5

\(x\)	\(f(x)=\sqrt[3]{x}\)	\((x,f(x))\)
\ (x\) ">\(-1\)	\ (f (x) =\ sqrt [3] {x}\) ">\(f(\color{blue}{-1}\color{black}{})=-1\)	\ ((x, f (x))\) ">\((-1,-1)\)
\ (x\) ">\(0\)	\ (f (x) =\ sqrt [3] {x}\) ">\(f(\color{blue}{0}\color{black}{})=0\)	\ ((x, f (x))\) ">\((0,0)\)
\ (x\) ">\(1\)	\ (f (x) =\ sqrt [3] {x}\) ">\(f(\color{blue}{1}\color{black}{})=1\)	\ ((x, f (x))\) ">\((1,1)\)

Trazar los pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Esta función se parece a la función de cubo, pero volteada y ¡\(90^{\circ}\)a la derecha! Llamamos a esta función función de raíz cúbica. por la raíz en el radical. Como vemos no hay restricciones a la gráfica, el dominio es todo números reales o\((−∞, ∞)\).

Figura 5.4.6

Ejemplo 5.4.7

Grafica\(f(x) =\dfrac{1}{x}\) y determina el dominio.

Solución

Escojamos\(x\) -coordenadas, y busquemos\(y\) -valores correspondientes.

Tabla 5.4.6

\(x\)	\(f(x)=\dfrac{1}{x}\)	\((x,f(x))\)
\ (x\) ">\(-3\)	\ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{-3}\color{black}{})=-\dfrac{1}{3}\)	\ ((x, f (x))\) ">\((-3,-\dfrac{1}{3})\)
\ (x\) ">\(-2\)	\ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{-2}\color{black}{})=-\dfrac{1}{2}\)	\ ((x, f (x))\) ">\((-2,-\dfrac{1}{2})\)
\ (x\) ">\(-1\)	\ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{-1}\color{black}{})=-1\)	\ ((x, f (x))\) ">\((-1,-1)\)
\ (x\) ">\(0\)	\ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{0}\color{black}{})=\text{undefined}\)	\ ((x, f (x))\) ">sin punto
\ (x\) ">\(1\)	\ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{1}\color{black}{})=1\)	\ ((x, f (x))\) ">\((1,1)\)
\ (x\) ">\(2\)	\ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{2}\color{black}{})=\dfrac{1}{2}\)	\ ((x, f (x))\) ">\((2,\dfrac{1}{2})\)
\ (x\) ">\(3\)	\ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{3}\color{black}{})=\dfrac{1}{3}\)	\ ((x, f (x))\) ">\((3,\dfrac{1}{3})\)

Trazar los pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Esta gráfica se ve más diferente a las otras funciones y es porque es una fracción con una variable en el denominador. Recordemos, las fracciones no pueden tener cero en sus denominadores porque es entonces cuando las fracciones están indefinidas. Aprenderemos más sobre estas funciones que se denominan funciones racionales. Por ahora, llamamos a la gráfica de esta función función recíproca. Ya que vemos que esta función no puede tener cero en el denominador, y, a partir de la tabla, vemos cuándo\(x = 0\), la función está indefinida, entonces el dominio es todo números reales excepto para\(x = 0: \{x|x \neq 0\}\) o\((−∞, 0) ∪ (0, ∞)\).

Figura 5.4.7

Biblioteca de Funciones Tareas

A continuación se presentan las gráficas de funciones.

Figura 5.4.8

Ejercicio 5.4.1

Coincidir cada gráfica con el nombre de su función.

Nombres de las funciones

1. Función Recíproca
2. Función de valor absoluto
3. Función Raíz Cube
4. Función Cube
5. Función Constante
6. Función Identidad
7. Función Raíz Cuadrada
8. Función Cuadrada
9. Función lineal

Ejercicio 5.4.2

Coincidir cada gráfica con la fórmula de la función.

Fórmulas de funciones

1. \(f(x) = x\)
2. \(f(x) = −4\)
3. \(f(x) = |x|\)
4. \(f(x) = x^2\)
5. \(f(x) =\dfrac{1}{x}\)
6. \(f(x) = x^3\)
7. \(f(x) = mx + b\)
8. \(f(x) =\sqrt[3]{x}\)
9. \(f(x) =\sqrt{x}\)

Ejercicio 5.4.3

¿Cuáles son los dominios para cada una de las funciones?