11.4: Funciones cuadráticas de la gráfica
- Page ID
- 117432
Recordemos la parábola del capítulo Funciones.
Gráfica\(f(x)=x^2\).
Solución
Escojamos cinco\(x\) coordenadas y busquemos\(y\) los valores correspondientes. Cada\(x\) valor es positivo, negativo y cero. Esta es una práctica común, pero no requerida.
| \(x\) | \(f(x)=x^2\) | \((x,f(x))\) |
|---|---|---|
| \ (x\) ">\(-2\) | \ (f (x) =x^2\) ">\(f(\color{blue}{-2}\color{black}{)}=4\) | \ ((x, f (x))\) ">\((-2,4)\) |
| \ (x\) ">\(-1\) | \ (f (x) =x^2\) ">\(f(\color{blue}{-1}\color{black}{)}=1\) | \ ((x, f (x))\) ">\((-1,1)\) |
| \ (x\) ">\(0\) | \ (f (x) =x^2\) ">\(f(\color{blue}{0}\color{black}{)}=0\) | \ ((x, f (x))\) ">\((0,0)\) |
| \ (x\) ">\(1\) | \ (f (x) =x^2\) ">\(f(\color{blue}{1}\color{black}{)}=1\) | \ ((x, f (x))\) ">\((1,1)\) |
| \ (x\) ">\(2\) | \ (f (x) =x^2\) ">\(f(\color{blue}{2}\color{black}{)}=4\) | \ ((x, f (x))\) ">\((2,4)\) |
Trazar los cinco pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Esta gráfica se llama parábola y como esta función es bastante común para la\(x^2\) forma -form, la llamamos función cuadrática (cuadrada).
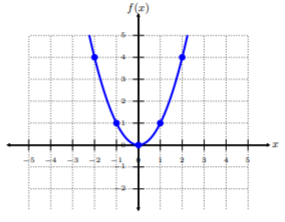
Dado que las funciones cuadráticas tienen un término principal que contiene\(x^2\), entonces el gráfico de una función cuadrática se llama parábola al igual que en el capítulo Funciones.
Una función cuadrática es una función polinómica de la forma
\[f(x)=ax^2+bx+c\nonumber\]
donde\(a\neq 0\).
En Ejemplo 11.4.1 , trazamos puntos y conectamos los puntos. Esta es una forma de graficar las funciones cuadráticas, pero no la más eficiente. Por lo tanto, podemos graficar fácilmente las funciones cuadráticas encontrando elementos clave de la función: vértice,\(x\) -intercepts y\(y\) -intercept.
Vértice de una función cuadrática
El vértice de una función cuadrática\(f(x)=ax^2+bx+x\) viene dado por
\[\left(-\dfrac{b}{2a},f\left(-\dfrac{b}{2a}\right)\right)\nonumber\]
Encuentra el vértice de\(f(x) = x^2 − 3x − 4\).
Solución
La\(x\) coordenada -del vértice viene\(−\dfrac{b}{2a}\) dada por la definición. En este caso,\(a = 1\),\(b = −3\), y\(c = −4\). Por lo tanto,
\[x=-\dfrac{b}{2a}=-\dfrac{-3}{2(1)}=\dfrac{3}{2}\nonumber\]
La\(y\) coordenada -del vértice es
\[f\left(\dfrac{3}{2}\right)=\left(\dfrac{3}{2}\right)^2-3\left(\dfrac{3}{2}\right)-4=-\dfrac{25}{4}\nonumber\]
Así, el vértice de\(f(x)\) está en\(\left(\dfrac{3}{2},-\dfrac{25}{4}\right)\). Echemos un vistazo a la gráfica y verifiquemos que esta es la ubicación del vértice. Vemos que el vértice está, de hecho, ubicado en\(\left(\dfrac{3}{2},-\dfrac{25}{4}\right)\). Adicionalmente, vemos que la parábola cruza el\(x\) eje -en\(x = −1\) y\(x = 4\), y el\(y\) -eje en\((0, −4)\).
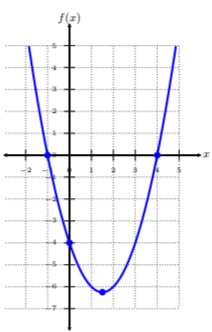
Graficar las funciones cuadráticas por sus propiedades
Para graficar una función cuadrática\(f(x) = ax^2 + bx + x\), por sus propiedades, obtenemos propiedades clave.
Inmueble 1. La dirección de la parábola.
- Si\(a > 0\), entonces la gráfica es una parábola ascendente.
- Si\(a < 0\), entonces la gráfica es una parábola descendente.
Propiedad 2. El vértice:\(\left(-\dfrac{b}{2a},f\left(-\dfrac{b}{2a}\right)\right)\)
Propiedad 3. La\(y\) -intercepción:\((0, f(0))\)
Propiedad 4. El\(x\) -intercepta:\((x, 0)\), es decir\(f(x) = 0\), donde, también conocido como los ceros de\(f(x)\).
Propiedad 5. El eje de simetría:\(x = −\dfrac{b}{2a}\)
El eje de simetría es una línea vertical que cruza el vértice de la parábola. De ahí, la línea\(x=-\dfrac{b}{2a}\). El eje de simetría esencialmente “corta” la parábola por la mitad y la parábola es simétrica alrededor de este eje.
Usando las propiedades, grafica\(f(x)=x^2+4x+3\).
Solución
Inmueble 1. La dirección de la parábola. Desde\(a = 1\) y\(a > 0\), entonces\(f(x)\) es una parábola hacia arriba.
Propiedad 2. Encuentra el vértice. Utilizamos la fórmula para encontrar el vértice, dónde\(a = 1\) y\(b = 4\). \[\begin{array}{rl}x=-\dfrac{b}{2a}&\text{Plug-n-chug} \\ x=-\dfrac{\color{blue}{4}}{\color{blue}{(2)(1)}}&\color{black}{\text{Simplify}} \\ x=-2&\text{The }x\text{-coordinate of the vertex}\end{array}\nonumber\]A continuación, encontramos la\(y\) coordenada -del vértice mediante la obtención\(f(-2)\). \[\begin{array}{rl}f(x)=x^2+4x+3&\text{Plug-n-chug} \\ f(\color{blue}{-2}\color{black}{)}=(\color{blue}{-2}\color{black}{)}^2+4(\color{blue}{-2}\color{black}{)}+3&\text{Evaluate} \\ f(-2)=-1&\text{The }y\text{-coordinate of the vertex}\end{array}\nonumber\]De ahí que el vértice sea\((-2,-1)\).
Propiedad 3. Encuentra la\(y\) -intercepción. Podemos encontrar la\(y\) -intercepción obteniendo\(f(0)\). \[\begin{array}{rl}f(x)=x^2+4x+3&\text{Plug-n-chug }x=0 \\ f(\color{blue}{0}\color{black}{)}=\color{blue}{0}\color{black}{^2}+4(\color{blue}{0}\color{black}{)}+3 &\text{Evaluate} \\ f(0)=3&\text{The }y\text{-intercept}\end{array}\nonumber\]De ahí que la\(y\) -intercepción sea\((0,3)\).
Propiedad 4. Encuentra las\(x\) -intercepciones. Podemos encontrar la\(x\) -intercepción obteniendo dónde\(f(x) = 0\). \[\begin{array}{rl} f(x)=x^2+4x+3&\text{Plug-n-chug }f(x)=0 \\ 0=x^2+4x+3&\text{Factor} \\ 0=(x+3)(x+1)&\text{Apply the zero product rule} \\ x+3=0\quad\text{and}\quad x+1=0&\text{Solve each equation} \\ x=-3\quad\text{and}\quad x=-1&\text{The }x\text{-intercepts}\end{array}\nonumber\]De ahí que las\(x\) -intercepciones sean\((-3,0)\) y\((-1,0)\).
Propiedad 5. Encuentra el eje de simetría. Vemos desde el vértice en la Propiedad 2. \(x = −2\). Así, el eje de simetría es la línea vertical\(x = −2\).
Vamos a graficar todas las propiedades y etiquetar cada propiedad.
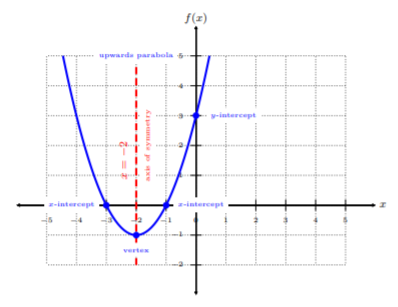
Entonces, verificamos que\(f(x)\) es una parábola hacia arriba con\(x\) -intercepciones\((−3, 0)\) y\((−1, 0)\),\(y\) -interceptar\((0, 3)\), vértice\((−2, −1)\), y eje de simetría\(x = −2\).
Usando las propiedades, grafica\(g(x) = −3x^2 + 12x − 9\).
Solución
Inmueble 1. La dirección de la parábola. Desde\(a = −3\) y\(a < 0\), entonces\(g(x)\) es una parábola hacia abajo.
Propiedad 2. Encuentra el vértice. Utilizamos la fórmula para encontrar el vértice, dónde\(a = −3\) y\(b = 12\). \[\begin{array}{rl}x=-\dfrac{b}{2a}&\text{Plug-n-chug} \\ x=-\dfrac{\color{blue}{12}}{\color{blue}{2(-3)}}&\text{Simplify} \\ x=2&\text{The }x\text{-coordinate of the vertex}\end{array}\nonumber\]A continuación, encontramos la\(y\) coordenada -del vértice mediante la obtención\(g(2)\). \[\begin{array}{rl}g(x)=-3x^2+12x-9&\text{Plug-n-chug} \\ g(\color{blue}{2}\color{black}{)}=-3(\color{blue}{2}\color{black}{)}^2+12(\color{blue}{2}\color{black}{)}-9&\text{Evaluate} \\ g(2)=3&\text{The }y\text{-coordinate of the vertex}\end{array}\nonumber\]De ahí que el vértice sea\((2,3)\).
Propiedad 3. Encuentra la\(y\) -intercepción. Podemos encontrar la\(y\) -intercepción obteniendo\(f(0)\). \[\begin{array}{rl}g(x)=-3x^2+12x-9&\text{ Plug-n-chug }x=0 \\ g(\color{blue}{0}\color{black}{)}=-3\color{blue}{0}\color{black}{^2}+12(\color{blue}{0}\color{black}{)}-9&\text{Evaluate} \\ g(0)=-9&\text{The }y\text{-intercept}\end{array}\nonumber\]De ahí que la\(y\) -intercepción sea\((0,-9)\).
Propiedad 4. Encuentra las\(x\) -intercepciones. Podemos encontrar la\(x\) -intercepción obteniendo dónde\(g(x) = 0\). \[\begin{array}{rl} g(x)=-3x^2+12x-9&\text{Plug-n-chug }g(x)=0 \\ 0=-3x^2+12x-9&\text{Factor a GCF of }-3 \\ =-3(x^2-4x+3)&\text{Divide each side by }-3\text{, then factor} \\ 0=(x-3)(x-1)&\text{Apply the zero product rule} \\ x-3=0\quad\text{and}\quad x-1=0&\text{Solve each equation} \\ x=3\quad\text{and}\quad x=1&\text{The }x\text{-intercepts}\end{array}\nonumber\]De ahí que las\(x\) -intercepciones sean\((3,0)\) y\((1,0)\).
Propiedad 5. Encuentra el eje de simetría. Vemos desde el vértice en la Propiedad 2. \(x = 2\). Así, el eje de simetría es la línea vertical\(x = 2\).
Vamos a graficar todas las propiedades y etiquetar cada propiedad.
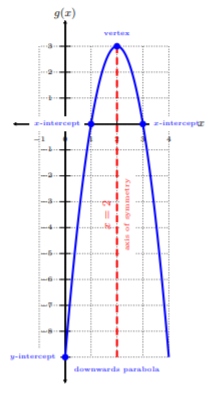
Entonces, verificamos que\(g(x)\) es una parábola hacia abajo con\(x\) -intercepciones\((3, 0)\) y\((1, 0)\),\(y\) -intercepción\((0, −9)\), vértice\((2, 3)\), y eje de simetría\(x = 2\).
Gráfica funciones cuadráticas por transformaciones
Una función cuadrática en forma de vértice se da como
\[f(x)=a(x-h)^2+k,\nonumber\]
donde el dominio consta de todos los números reales y\((h, k)\) es el vértice.
Recordar. En el capítulo con funciones racionales, representamos funciones racionales con desplazamiento horizontal y vertical. Llevemos esto un paso más allá, y graficemos las funciones cuadráticas no solo con desplazamientos horizontales y verticales, sino también con un estiramiento o compresión.
Dada\(f(x)\) es la función cuadrática en forma de vértice
\[f(x)=a(x-h)^2+k,\nonumber\]
los desplazamientos horizontales y verticales y los estiramientos o compresiones verticales de\(f(x)\) se describen a continuación:
| \(f(x-h)\) | \(f(x)\pm k\) | \(af(x)\) | |
|---|---|---|---|
| Transformación | \ (f (x-h)\) ">Desplazamiento horizontal | \ (f (x)\ pm k\) ">Desplazamiento vertical | \ (af (x)\) ">Estiramiento o compresión vertical |
| Unidades | \ (f (x-h)\) ">\(h>0\): Desplazar\(h\) unidades a la derecha \(h<0\): Desplazar\(h\) unidades a la izquierda |
\ (f (x)\ pm k\) ">\(k>0\): Desplazar\(k\) unidades hacia arriba \(k<0\): Desplazar\(k\) unidades hacia abajo |
\ (af (x)\) ">\(|a|>1\): Multiplicar todas las salidas por\(a\); estiramiento vertical \(0<|a|<1\): Multiplicar todas las salidas por\(a\); compresión vertical |
Recordemos de la subsección anterior, si\(a > 0\), la parábola está hacia arriba y si\(a < 0\), la parábola es hacia abajo.
Usando la función de biblioteca\(f(x)=x^2\), graph\(g(x)=x^2+2\).
Solución
Comenzamos notando que estamos sumando\(2\) a\(f(x)\), es decir,\(g(x) = f(x) + 2\):
\[\begin{aligned}g(x)&=x^2+2 \\ g(x)&=f(x)+2\end{aligned}\]
Esto significa que, desde la mesa,\(g(x)\) tiene un desplazamiento vertical por\(2\) unidades hacia arriba. Empecemos con\(f(x) = x^2\), y luego cambiemos\(f(x)\)\(2\) las unidades hacia arriba para obtener\(g(x)\):
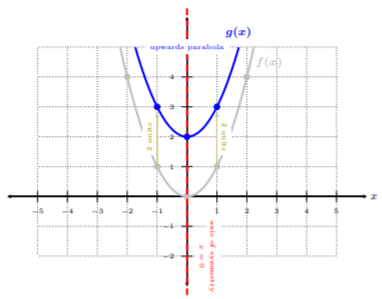
Podemos ver que el gráfico sólido azul es\(g(x)\), donde\(g(x)\) está una parábola ascendente, el eje de simetría es\(x = 0\). Observe, todos los puntos en\(f(x)\) desplazados hacia arriba por\(2\) unidades. Podemos usar los puntos bien definidos de la función de biblioteca\(f(x) = x^2\) para transformarnos en\(g(x)\).
Usando la función de biblioteca\(f(x) = x^2\), graph\(h(x) = (x − 3)^2 + 2\).
Solución
Comenzamos notando que estamos sumando\(2\)\(f(x)\) y restando\(3\) de la entrada\(x\), es decir,\(h(x) = f(x − 3) + 2\):
\[\begin{aligned}h(x)&=(x-3)^2+2 \\ h(x)&=f(x-3)+2\end{aligned}\]
Esto significa que, desde la mesa,\(h(x)\) tiene un desplazamiento horizontal hacia la derecha por\(3\) unidades, y desplazamiento vertical por\(2\) unidades hacia arriba. Empecemos con\(f(x) = x^2\), y luego desplazemos\(f(x)\)\(3\) las unidades hacia la derecha, y\(2\) las unidades hacia arriba para obtener\(h(x)\):
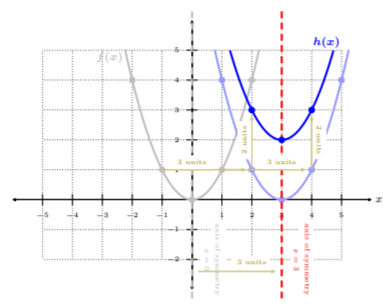
Podemos ver que el gráfico sólido azul es\(h(x)\), donde\(h(x)\) está una parábola ascendente, el eje de simetría es\(x = 3\). Observe, todos los puntos en\(f(x)\) desplazados a la derecha por\(3\) unidades y hacia arriba por\(2\) unidades. Podemos usar los puntos bien definidos de la función de biblioteca\(f(x) = x^2\) para transformarnos en\(h(x)\).
Usando la función de biblioteca\(f(x) = x^2\), graph\(k(x) = −2(x + 1)^2 − 3\).
Solución
Comenzamos notando que estamos restando\(f(x)\), estirando\(3\) verticalmente por un factor de\(−2\), y sumando\(1\) a la entrada\(x\), es decir,\(k(x) = −2\cdot f(x + 1) − 3\):
\[\begin{aligned} k(x)&=-2(x+1)^2-3 \\ k(x)&=-2\cdot f(x+1)-3\end{aligned}\]
Esto significa que, desde la mesa,\(k(x)\) tiene un desplazamiento horizontal hacia la izquierda por\(1\) unidad, un estiramiento vertical por un factor de\(−2\), y un desplazamiento vertical por\(3\) unidades hacia abajo. Empecemos con\(f(x) = x^2\), y luego apliquemos estas transformaciones para obtener\(k(x)\). Dado que hay tres transformaciones, lo mejor es que dividamos esto en tres pasos.
Paso 1. Grafique la función de biblioteca\(f(x)=x^2\),, y aplique el desplazamiento horizontal:\(f(x+1)\).
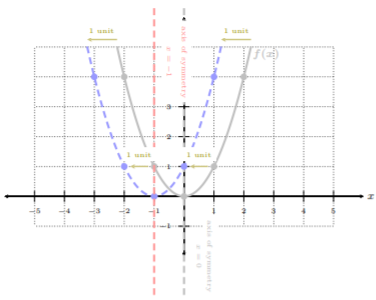
Paso 2. Gráfica\(f(x + 1)\) del Paso 1. , y aplicar el estiramiento vertical, es decir, multiplicar las\(y\) coordenadas -de los pares ordenados bien definidos por\(−2\):\(−2\cdot f(x + 1)\)
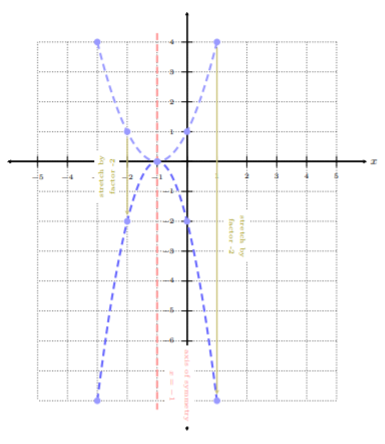
Paso 3. Gráfica\(−2\cdot f(x + 1)\) del Paso 2. , y aplicar el desplazamiento vertical:\(−2\cdot f(x + 1) − 3\)
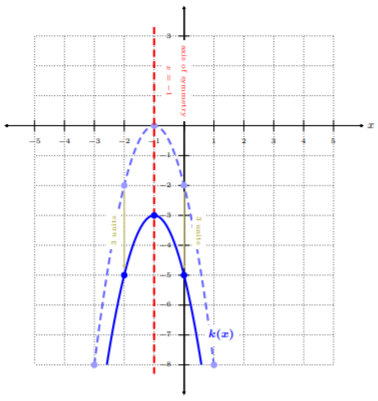
Podemos ver que el gráfico sólido azul es\(k(x)\), donde\(k(x)\) está una parábola descendente, el eje de simetría es\(x = −1\). Observe, todos los puntos\(f(x)\) desplazados a la izquierda por\(1\) unidad, estirados por un factor de\(−2\), y desplazados hacia abajo por\(3\) unidades.
Observe con tres transformaciones, puede llegar a ser tedioso y complicado. La mejor ruta para aplicar múltiples transformaciones es seguir el orden de las operaciones, por ejemplo, primer paréntesis, multiplicación/división y luego sución/resta. Con transformaciones, esto se traduce en
Paso 1. Aplicar el desplazamiento horizontal
Paso 2. Estirar o comprimir verticalmente la función
Paso 3. Por último, aplicar el desplazamiento vertical
Una manera de recordar el orden en que aplicamos las transformaciones es\(hak\): primero la\(h\), luego\(a\), por último,\(k\).
Gráfica Cuadrática Funciones Tareas
Grafica la función cuadrática usando las propiedades. Asegúrate de etiquetar tu gráfica con todas las propiedades.
\(f(x)=x^2-2x-8\)
\(f(x)=2x^2-12x+10\)
\(f(x)=-2x^2+12x-18\)
\(f(x)=-3x^2+24x-45\)
\(f(x)=-x^2+4x+5\)
\(f(x)=-x^2+6x-5\)
\(f(x)=-2x^2+16x-24\)
\(f(x)=3x^2+12x+9\)
\(f(x)=5x^2-40x+75\)
\(f(x)=-5x^2-60x-175\)
\(f(x)=x^2-2x-3\)
\(f(x)=2x^2-12x+16\)
\(f(x)=-2x^2+12x-10\)
\(f(x)=-3x^2+12x-9\)
\(f(x)=-x^2+4x-3\)
\(f(x)=-2x^2+16x-30\)
\(f(x)=2x^2+4x-6\)
\(f(x)=5x^2+30x+45\)
\(f(x)=5x^2+20x+15\)
\(f(x)=-5x^2+20x-15\)
Comenzando con la función de biblioteca\(y=x^2\), declarar la función,\(f(x)\), dada su (s) transformación (es).
estirado verticalmente por un factor de\(3\) y desplazado hacia la derecha\(1\)
estirado verticalmente por un factor de\(-2\), y desplazado a la izquierda\(3\)
comprimido verticalmente por un factor de\(\dfrac{1}{3}\)
estirado verticalmente por un factor de\(2\) y desplazado hacia la derecha\(4\)
estirado verticalmente por un factor de\(4\), desplazado a la izquierda\(4\)
comprimido verticalmente por un factor de\(−\dfrac{1}{2}\) y desplazado hacia arriba por\(3\) unidades
estirado verticalmente por un factor de\(3\) y desplazado hacia abajo\(4\)
estirada verticalmente por un factor de\(2\), desplazada hacia la derecha\(3\) y desplazada hacia arriba\(1\)
Comenzando con la función de biblioteca\(y=x^2\), grafica la función usando transformaciones.
\(g(x)=-\dfrac{1}{2}(x+7)^2\)
\(g(x)=2(x-1)^2-2\)
\(y=\dfrac{1}{5}(x-2)^2\)
\(f(x)=\dfrac{1}{2}(x+2)^2+9\)
\(f(x)=2(x+4)^2-5\)
\(f(x)=-2(x-4)^2+7\)
\(g(x)=2(x-3)^2-2\)
\(g(x)=-\dfrac{1}{2}(x+5)^2\)
\(f(x)=\dfrac{1}{2}(x+4)^2+8\)
\(f(x)=-2(x-8)^2+7\)


