11.5: Desigualdades cuadráticas
- Page ID
- 117437
Podemos pensar en un capítulo anterior donde obtuvimos soluciones para desigualdades lineales donde las soluciones son intervalos de números. Con las desigualdades cuadráticas, es similar a las desigualdades lineales, pero, ahora, en lugar de líneas, tenemos parábolas. Por lo tanto, tenemos dos métodos para resolver desigualdades cuadráticas: graficar o algebraicamente.
Resolver desigualdades cuadráticas mediante gráficos
Podemos usar los ceros (o raíces) de una gráfica de una ecuación cuadrática para resolver desigualdades cuadráticas. Recordemos, los ceros (o raíces) de una gráfica son las\(x\) -intercepciones, es decir,\(y = 0\).
Resuelve\(x^2 − 3x − 4\geq 0\) usando el método de graficación.
Solución
Primero comenzamos por graficar\(x^2 − 3x − 4\) como lo haríamos en la sección anterior. Recordemos, la\(x\) coordenada -del vértice es\(−\dfrac{b}{2a}\). Por lo tanto,
\[-\dfrac{b}{2a}=-\dfrac{-3}{2(1)}=\dfrac{3}{2}=1.5\nonumber\]
La\(y\) coordenada -del vértice se\(x^2 − 3x − 4\) evalúa para\(x = 1.5\):
\[(1.5)^2-3(1.5)-4=-6.25\nonumber\]
El vértice está en\((1.5, −6.25)\). La\(y\) -intercepción es cuando\(x = 0\):
\[0^2-3(0)-4=-4\nonumber\]
y las\(x\) -intercepciones son cuándo\(x^2 − 3x − 4 = 0\). Resolviendo por las raíces que obtenemos
\[\begin{aligned}x^2-3x-4&=0 \\ (x-4)(x+1)&=0 \\ x-4=0\quad&\text{or}\quad x+1=0 \\ x=4\quad&\text{or}\quad x=-1\end{aligned}\]
Así, las intercepciones son\((0, −4),\: (4, 0),\) y\((−1, 0)\) con un vértice en\((1.5, −6.25)\). Ahora dibujamos la gráfica:
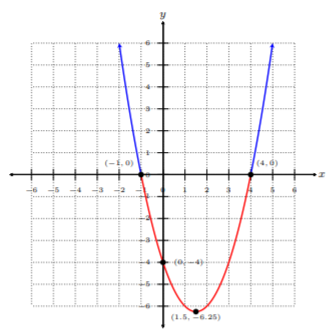
Dado\(x^2 − 3x − 4\geq 0\) dice estamos buscando específicamente los valores de\(x^2 − 3x − 4\) en los que son mayores o iguales a cero. En otras palabras, estamos buscando todos los\(y\) -valores que están por encima del\(x\) eje -porque ahí es donde todos los\(y\) -valores son positivos. Mirando la gráfica anterior, estos son todos los valores en las partes azules de la gráfica. Así, utilizando el método de graficación, la solución es\((−∞, −1] ∪ [4, ∞)\). Tenga en cuenta que utilizamos corchetes ya que es\(\geq\).
Observe, ignoramos la parte roja de la parábola ya que aquí es donde\(x^2 − 3x − 4\) está negativo, es decir, todos los\(y\) valores -son negativos, porque solo estábamos buscando cuándo\(x^2 − 3x − 4\geq 0\), las partes de la gráfica por encima del\(x\) eje -eje.
Resolver desigualdades cuadráticas algebraicamente
El siguiente método para resolver las desigualdades cuadráticas es algebraicamente. De ahí que haya un poco más de trabajo involucrado ya que el método es algebraico. Debemos seguir un orden de pasos para obtener la solución correcta. La buena noticia es que estos dos métodos son similares donde siempre usamos las\(x\) -intercepciones para determinar los intervalos.
Paso 1. Reescribe la desigualdad para que\(ax^2 + bx + c\) quede en un lado y el cero esté en el otro.
Paso 2. Determinar dónde la desigualdad es cero utilizando cualquier método apropiado.
Paso 3. Utilice los\(x\) valores -obtenidos en el paso anterior para etiquetar en una recta numérica.
Paso 4. Tomar valores de prueba para observar dónde es verdadera la desigualdad.
- Si la desigualdad es\(< 0\) o\(\leq 0\), entonces la desigualdad es verdadera donde los valores de prueba son negativos.
- Si la desigualdad es\(> 0\) o\(\geq 0\), entonces la desigualdad es verdadera donde los valores de prueba son positivos.
Paso 5. Escribe la solución en notación de intervalos.
Resolver algebraicamente:\(-x^2+8>2x\)
Solución
Paso 1. Reescribimos\(−x^2 + 8 > 2x\) para que el cero esté en un lado:\[-x^2-2x+8>0\nonumber\]
Paso 2. Establecemos el lado izquierdo igual a cero para obtener las raíces (o ceros):\[\begin{aligned} -x^2-2x+8&=0 \\ x^2+2x-8&=0 \\ (x+4)(x-2)&=0 \\ x+4=0\quad&\text{or}\quad x-2=0 \\ x=-4\quad&\text{or}\quad x=2\end{aligned}\]
Paso 3. Etiqueta\(-4\) y\(2\) en una línea numérica en blanco:

Paso 4. Tomamos valores de prueba en cada lado de\(−4\) y\(2\). Vamos a elegir números bastante fáciles como\(−5,\: 0\), y\(3\). Enchufamos estos números\(−x^2 − 2x + 8\) y determinamos si el valor es positivo o negativo:
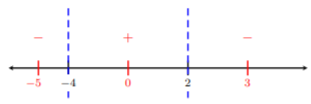
\[\begin{aligned} -(-5)^2-2(-5)+8&=-7<0\quad\Longrightarrow\quad\text{letting }x=-5 \\ -(0)^2-2(0)+8&=8>0\quad\Longrightarrow\quad\text{letting }x=0 \\ -(3)^2-2(3)+8&=-7<0\quad\Longrightarrow\quad\text{letting }x=3\end{aligned}\]
Paso 5. Desde\(−x^2 − 2x + 8 > 0\) (del Paso 1. ), entonces estamos buscando donde los valores de la prueba sean positivos. Mirando la recta numérica anterior, vemos que estos son los valores intermedios\(−4\) y\(2\). Así, la solución es\((−4, 2)\). Tenga en cuenta que usamos paréntesis ya que el símbolo de desigualdad es\(>\).
Tareas de desigualdades cuadráticas
Resolver la desigualdad. Escribe la solución en notación de intervalos.
\(x^2-9x+18>0\)
\(x^2-2x-24\leq 0\)
\(x^2-2x-3<0\)
\(x^2+10x+24\geq 0\)
\(x^2-4x+4>0\)
\(x^2+2x\geq 8\)
\(x^2-4x\leq -3\)
\(3x^2+7x-20\leq 0\)
\(4x^2+11x-20\geq 0\)
\(3x^2+2x-1<0\)
\(-4x^2+7x\geq 0\)
\(x^2+6x\geq 0\)
\(x^2-12x+36<0\)
\(x^2-2x+1\geq 0\)


