Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

1.3: Factorización Prime

Última actualización

30 oct 2022
Guardar como PDF
- 1.2: Factores, productos y exponentes
- 1.4: El múltiplo menos común

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Visión general

Números primos y compuestos
El principio fundamental de la aritmética
La factorización principal de un número entero

Números primos y compuestos

Observe que los únicos factores de 7 son 1 y 7 en sí, y que los únicos factores de 23 son el 1 y el 23 mismo.

Definición: Prime Number

Un número entero mayor que 1 cuyo único número entero son factores en sí mismo y 1 se llama número primo.

Los primeros siete números primos son

2, 3, 5, 7, 11, 13 y 17

El número 1 no se considera un número primo, y el número 2 es el primer y único número primo par.
Muchos números tienen factores distintos a ellos mismos y 1. Por ejemplo, los factores de 28 son 1, 2, 4, 7, 14 y 28 (ya que cada uno de estos números enteros y solo estos números enteros se dividen en 28 sin un resto).

Definición: Número compuesto

Un número entero que se compone de factores distintos a sí mismo y 1 se llama número compuesto. Los números compuestos no son números primos.

Algunos números compuestos son 4, 6, 8, 10, 12 y 15.

El principio fundamental de la aritmética

Los números primos son muy importantes en el estudio de las matemáticas. Pronto los usaremos en nuestro estudio de fracciones. Ahora, sin embargo, seremos introducidos a un importante principio matemático.

Definición: El principio fundamental de la aritmética

Excepto por el orden de los factores, cada número entero, distinto del 1, se puede factorizar de una y sólo una manera como producto de números primos.

Definición: Factorización Prime

Cuando se descompone un número para que todos sus factores sean números primos, la factorización se llama la factorización primo del número.

Conjunto de Muestras A

Ejemplo $\PageIndex{1}$

Encuentra la factorización prima de 10.

$10=2 · 5$

Tanto el 2 como el 5 son números primos. Así, 2 · 5 es la factorización primo de 10.

Ejemplo $\PageIndex{2}$

Encuentra la factorización prime de 60.

60 = 2 · 30 30 no es primo. 30 = 2 · 15

= 2 · 2 · 15 15 no es primo. 15 = 3 · 5

= 2 · 2 · 3 · 5 Usaremos exponentes. 2 · 2 = $2^2$

= $2^2$ · 3 · 5

Los números 2, 3 y 5 son todos primos. Así, 2 ² · 3 · 5 es la factorización prima de 60.

Ejemplo $\PageIndex{3}$

Encuentra la factorización prima de 11.

11 es un número primo. La factorización de primos se aplica solo a los números compuestos.

La factorización principal de un número entero

El siguiente método proporciona una manera de encontrar la factorización prima de un número entero. Los ejemplos que siguen utilizarán el método y lo dejarán más claro.

Divide el número repetidamente por el número primo más pequeño que se dividirá en el número sin un resto.
Cuando el número primo utilizado en el paso 1 ya no se divida en el número dado sin un resto, repita el proceso con el siguiente número primo más grande.
Continuar con este proceso hasta que el cociente sea 1.
La descomposición como primo del número dado es el producto de todos estos divisores primos. 

Conjunto de Muestras B

Ejemplo $\PageIndex{4}$

Encuentra la factorización prime de 60.

Dado que 60 es un número par, es divisible por 2. Vamos a dividir repetidamente por 2 hasta que ya no podamos (cuando empecemos a conseguir un resto). Dividiremos de la siguiente manera.

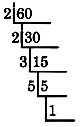
$La factorización prima de sesenta. Consulte el longdesc para una descripción completa.$

30 es divisible por 2 otra vez.

15 no es divisible por 2, pero es divisible por 3, el siguiente primo más grande.

5 no es divisible por 3, pero es divisible por 5, el siguiente primo más grande.

El cociente es 1 así que detenemos el proceso de división

La factorización prima de 60 es producto de todos estos divisores.

60 = 2 · 2 · 3 · 5 Utilizaremos exponentes cuando sea posible

60 = $2^2$ · 3 · 5

Ejemplo $\PageIndex{5}$

Encuentra la factorización prima de 441.

Dado que 441 es un número impar, no es divisible por 2. Intentaremos 3, el próximo prime más grande.

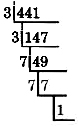
$La factorización prima de cuatrocientos cuarenta y uno. Consulte el longdesc para una descripción completa.$

147 es divisible por 3.

49 no es divisible por 3 ni por 5, sino por 7.

7 es divisible por 7.

El cociente es 1 así que detenemos el proceso de división.

La descomposición primo de 441 es el producto de todos los divisores.

441 = 3 · 3 · 7 · 7 Utilizaremos exponentes cuando sea posible.

441 = $3^2$ · $7^2$

Ejercicios

Para los siguientes problemas, determine qué números enteros son primos y cuáles son compuestos.

Ejercicio $\PageIndex{1}$

Contestar: prime

Ejercicio $\PageIndex{2}$

Contestar: compuesto

Ejercicio $\PageIndex{3}$

Contestar: compuesto

Ejercicio $\PageIndex{4}$

Contestar: prime

Ejercicio $\PageIndex{5}$

Contestar: prime

Ejercicio $\PageIndex{6}$

Contestar: prime

Ejercicio $\PageIndex{7}$

Contestar: prime

Ejercicio $\PageIndex{8}$

Contestar: compuesto

Ejercicio $\PageIndex{9}$

Contestar: prime

Ejercicio $\PageIndex{10}$

Contestar: compuesto

Ejercicio $\PageIndex{11}$

Contestar: compuesto

Ejercicio $\PageIndex{12}$

Contestar: compuesto

Ejercicio $\PageIndex{13}$

1044

Contestar: compuesto

Ejercicio $\PageIndex{14}$

339

Contestar: compuesto

Ejercicio $\PageIndex{15}$

209

Contestar: compuesto

Para los siguientes problemas, encuentra la factorización prima de cada número entero. Usar exponentes en factores repetidos.

Ejercicio $\PageIndex{16}$

Ejercicio $\PageIndex{17}$

Contestar: 2 · 19

Ejercicio $\PageIndex{18}$

Ejercicio $\PageIndex{19}$

Contestar: 2 · 31

Ejercicio $\PageIndex{20}$

Ejercicio $\PageIndex{21}$

176

Contestar: $2^4$ · $11$

Ejercicio $\PageIndex{22}$

480

Ejercicio $\PageIndex{23}$

819

Contestar: $3^2$ · $7$ · $13$

Ejercicio $\PageIndex{24}$

2025

Ejercicio $\PageIndex{25}$

148,225

Contestar: $5^2$ · $7^2$ · $11^2$

Visión general

Números primos y compuestos

Definición: Prime Number

Definición: Número compuesto

El principio fundamental de la aritmética

Definición: El principio fundamental de la aritmética

Definición: Factorización Prime

Conjunto de Muestras A

Ejemplo1.3.1\PageIndex{1}

Ejemplo1.3.2\PageIndex{2}

Ejemplo1.3.3\PageIndex{3}

La factorización principal de un número entero

Conjunto de Muestras B

Ejemplo1.3.4\PageIndex{4}

Ejemplo1.3.5\PageIndex{5}