1.7: Fracciones decimales

Última actualización
Guardar como PDF

Page ID: 112214

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Descripción general

Fracciones decimales
Sumando y restando fracciones decimales
Multiplicar fracciones decimales
Dividir fracciones decimales
Conversión de fracciones decimales en fracciones
Conversión de fracciones a fracciones decimales

Fracciones decimales

Las fracciones son una forma en que podemos representar partes de números enteros. Las fracciones decimales son otra forma de representar partes de números enteros.

Fracciones decimales

Una fracción decimal es una fracción en la que el denominador es una potencia de 10.

Una fracción decimal utiliza un punto decimal para separar partes enteras y partes fraccionarias. Las partes enteras se escriben a la izquierda del punto decimal y las partes fraccionarias se escriben a la derecha del punto decimal. Así como cada dígito en un número entero tiene un valor particular, también lo hacen los dígitos en posiciones decimales.

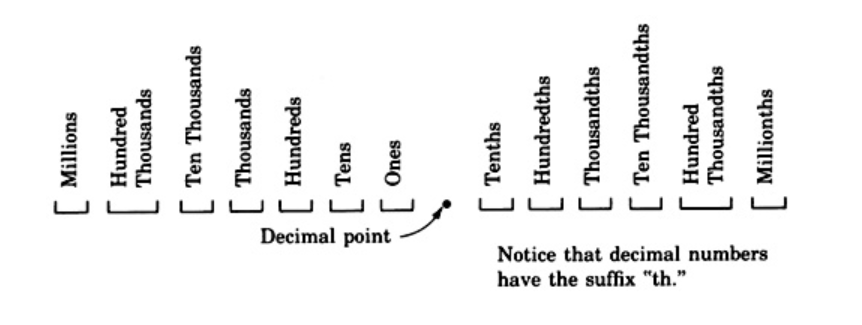
$clipboard_ea88b986766aeb75f89f9bd0ff13a57fa.png$

Conjunto de Muestras A

Los siguientes números son fracciones decimales

Ejemplo$\PageIndex{1}$

57.9

El 9 está en la décimas posición. 57.9 =$10\dfrac{9}{10}$.

Ejemplo$\PageIndex{2}$

6.8014

El 8 está en la posición décimas.

El 0 está en la posición de centésimas.

El 1 está en la posición milésimas.

El 4 está en la posición de las diez milésimas.

6.8014 =$6\dfrac{8014}{10000}$.

Sumando y restando fracciones decimales

Sumar/restar fracciones decimales:

Para sumar o restar fracciones decimales,

Alinee los números verticalmente para que los puntos decimales se alineen uno debajo del otro y las posiciones decimales correspondientes estén en la misma columna. Agrega ceros si es necesario.
Sumar o restar los números como si fueran números enteros.
Coloque un punto decimal en la suma o diferencia resultante directamente debajo de los otros puntos decimales.

Conjunto de Muestras B

Encuentra cada suma o diferencia

Ejemplo$\PageIndex{3}$

$clipboard_eb8f3187bed3dae27998d45d92fb02733.png$

Ejemplo$\PageIndex{4}$

$clipboard_e347c7001e47b6cc97bc4ef4184aad64f.png$

Ejemplo$\PageIndex{5}$

$clipboard_e78931fdcd0ab185080223fb89a946e6e.png$

Multiplicar fracciones decimales

Multiplicar fracciones decimales

Para multiplicar decimales,

Multiplique los números como si fueran números enteros.
Encuentra la suma del número de decimales en los factores.
El número de decimales en el producto es la suma que se encuentra en el paso 2.

Conjunto de Muestras C

Encuentra los siguientes productos

Ejemplo$\PageIndex{6}$

$clipboard_e9a2205a67b0ff9b184b9e94b27f5300c.png$

Ejemplo$\PageIndex{7}$

$clipboard_e7fe21e750898d21ed9851636a9a8e0c1.png$

Dividir fracciones decimales

Dividir fracciones decimales

Para dividir un decimal por un decimal distinto de cero,

Convierte el divisor a un número entero moviendo el punto decimal a la posición inmediatamente a la derecha del último dígito del divisor.
Mueve el punto decimal del dividendo a la derecha el mismo número de dígitos que se movió en el divisor.
Establezca el punto decimal en el cociente colocando un punto decimal directamente encima del punto decimal en el dividendo.
Dividir como de costumbre.

Conjunto de Muestras D

Encuentra los siguientes cocientes

Ejemplo$\PageIndex{8}$

$clipboard_ec5f32196849d2f0f6febf901572c5361.png$

Ejemplo$\PageIndex{9}$

$clipboard_e99cc7a86f383544f60a07a618f0dc751.png$

Ejemplo$\PageIndex{10}$

$clipboard_eddecf73ac4c0ceee99b1eed28da9da56.png$

Conversión de fracciones decimales en fracciones

Podemos convertir una fracción decimal en una fracción leyéndola y luego escribiendo la frase que acabamos de leer. Al leer la fracción decimal, observamos el valor posicional más alejado a la derecha. Quizá tengamos que reducir la fracción.

Juego de Muestras E

Convertir cada fracción decimal en una fracción

Ejemplo$\PageIndex{11}$

$clipboard_ee771b2283db4f531418ef8c383937923.png$

Ejemplo$\PageIndex{12}$

$clipboard_ea884cbe3facd91eae60ea788abe93444.png$

Conversión de fracciones a fracciones decimales

Conjunto de Muestras F

Convierte las siguientes fracciones a decimales. Si la división no termina, redondear a 2 decimales.

Ejemplo$\PageIndex{13}$

$clipboard_ef7a4e04a8fa9406d8f6ff9e0bb74ca7d.png$

Ejemplo$\PageIndex{14}$

$clipboard_e9f18a5e71406773c7600d66bfb1bca1e.png$

Ejemplo$\PageIndex{15}$

$clipboard_e22125b2b49cab4acb3a0cbebed1e39e1.png$

Ejemplo$\PageIndex{16}$

$clipboard_ea42278a4fe104364bee6a2d0c91d0e00.png$

Ejemplo$\PageIndex{17}$

$clipboard_ecb66dcc55e4885d631a5c0d6cdf38144.png$

Ejercicios

Para los siguientes problemas, realice cada operación indicada.

Ejercicio$\PageIndex{1}$

1.84 + 7.11

Contestar: 8.95

Ejercicio$\PageIndex{2}$

15.015 - 6.527

Ejercicio$\PageIndex{3}$

4.904 - 2.67

Contestar: 2.234

Ejercicio$\PageIndex{4}$

156.33 − 24.095

Ejercicio$\PageIndex{5}$

.0012 + 1.53 + 5.1

Contestar: 6.6312

Ejercicio$\PageIndex{6}$

44.98 + 22.8 − 12.76

Ejercicio$\PageIndex{7}$

5.0004 − 3.00004 + 1.6837

Contestar: 3.68406

Ejercicio$\PageIndex{8}$

1.11 + 12.1212 − 13.131313

Ejercicio$\PageIndex{9}$

4.26 ⋅ 3.2

Contestar: 13.632

Ejercicio$\PageIndex{10}$

2.97 ⋅ 3.15

Ejercicio$\PageIndex{11}$

23.05 ⋅ 1.1

Contestar: 25.355

Ejercicio$\PageIndex{12}$

5.009 ⋅ 2.106

Ejercicio$\PageIndex{13}$

0.1 ⋅ 3.24

Contestar: 0.324

Ejercicio$\PageIndex{14}$

100 ⋅ 12.008

Ejercicio$\PageIndex{15}$

1000 ⋅ 12.008

Contestar: 12,008

Ejercicio$\PageIndex{16}$

10,000 ⋅ 12.008

Ejercicio$\PageIndex{17}$

75.642 ÷ 18.01

Contestar: 4.2

Ejercicio$\PageIndex{18}$

51.811 ÷ 1.97

Ejercicio$\PageIndex{19}$

0.0000448 ÷ 0.014

Contestar: 0.0032

Ejercicio$\PageIndex{20}$

0.129516 ÷ 1004

Para los siguientes problemas, convierta cada fracción decimal a una fracción.

Ejercicio$\PageIndex{21}$

0.06

Contestar: $\dfrac{3}{50}$

Ejercicio$\PageIndex{22}$

0.115

Ejercicio$\PageIndex{23}$

3.7

Contestar: $3\dfrac{7}{10}$

Ejercicio$\PageIndex{24}$

48.1162

Ejercicio$\PageIndex{25}$

712.00004

Contestar: $712\dfrac{1}{25000}$

Para los siguientes problemas, convierta cada fracción a una fracción decimal. Si la forma decimal no termina, redondear a 3 decimales.

Ejercicio$\PageIndex{26}$

$\dfrac{5}{8}$

Ejercicio$\PageIndex{27}$

$\dfrac{9}{20}$

Contestar: 0.45

Ejercicio$\PageIndex{28$

15 ÷ 22

Ejercicio$\PageIndex{29}$

$\dfrac{7}{11}$

Contestar: 0.636

Ejercicio$\PageIndex{30}$

$\dfrac{2}{9}$

Search

Text Color

Text Size

Margin Size

Font Type

Fracciones decimales

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)

Ejemplo\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\)

Ejemplo\(\PageIndex{7}\)

Ejemplo\(\PageIndex{8}\)

Ejemplo\(\PageIndex{9}\)

Ejemplo\(\PageIndex{10}\)

Conversión de fracciones decimales en fracciones

Ejemplo\(\PageIndex{11}\)

Ejemplo\(\PageIndex{12}\)

Conjunto de Muestras F

Ejemplo\(\PageIndex{13}\)

Ejemplo\(\PageIndex{14}\)

Ejemplo\(\PageIndex{15}\)

Ejemplo\(\PageIndex{16}\)

Ejemplo\(\PageIndex{17}\)