7.4: Graficar ecuaciones lineales en dos variables
( \newcommand{\kernel}{\mathrm{null}\,}\)
Soluciones y Líneas
Sabemos que las soluciones a ecuaciones lineales en dos variables se pueden expresar como pares ordenados. De ahí que las soluciones se puedan representar por punto en el plano. También sabemos que la frase “graficar la ecuación” significa ubicar la solución a la ecuación dada en el plano. Considera la ecuacióny−2x=−3. Gráficaremos seis soluciones (pares ordenados) a esta ecuación en el sistema de coordenadas a continuación. Encontraremos las soluciones eligiendox -valores (de−1 a+4), sustituyéndolos en la ecuacióny−2x=−3, y luego resolviendo para obtener losy valores f correspondientes. Podemos realizar un seguimiento de los pares ordenados usando una tabla.
y−2x=−3
| Six= | Entoncesy= | Pares Pedidos |
| −1 | −5 | (−1, −5) |
| 0 | −3 | (0, −3) |
| 1 | −1 | (1, −1) |
| 2 | 1 | (2, 1) |
| 3 | 3 | (3, 3) |
| 4 | 5 | (4, 5) |
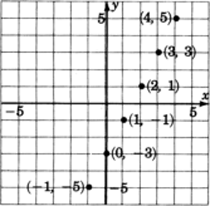
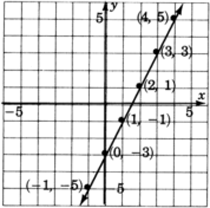
Hemos trazado sólo seis soluciones a la ecuacióny−2x=−3. Hay, como sabemos, infinitamente muchas soluciones. Al observar los seis puntos que hemos trazado, podemos especular sobre la ubicación de todos los demás puntos. Los seis puntos que trazamos parecen estar en línea recta. Esto nos llevaría a creer que todos los demás puntos (soluciones) también se encuentran en esa misma línea. En efecto, esto es cierto. De hecho, esta es precisamente la razón por la que las ecuaciones de primer grado se denominan ecuaciones lineales.
Línea
↕
Lineal
Forma general de una ecuación lineal
Existe una forma estándar en la que se escriben ecuaciones lineales en dos variables. Supongamos quea,b, yc son números reales y esoa yb no pueden ser ambos cero a la vez. Luego, la ecuación lineal en dos variables
ax+by=c
se dice que está en forma general.
Debemos estipular esoa yb no podemos ambos igualar cero a la vez, pues si lo fueran habríamos
0x+0y=c
0=c
Esta afirmación es cierta sólo sic=0. Sic fuera a ser cualquier otro número, obtendríamos una declaración falsa.
Ahora, tenemos lo siguiente:
La gráfica de todos los pares ordenados que resuelven una ecuación lineal en dos variables produce una línea recta.
Esto implica,
La gráfica de una ecuación lineal en dos variables es una línea recta.
De estas declaraciones podemos concluir,
Si un par ordenado es una solución a una ecuaciones lineales en dos variables, entonces se encuentra en la gráfica de la ecuación.
Además,
Cualquier punto (pares ordenados) que se encuentre en la gráfica de una ecuación lineal en dos variables es una solución a esa ecuación.
El método de interceptación de gráficos
Cuando queremos graficar una ecuación lineal, ciertamente no es práctico graficar infinitamente muchos puntos. Dado que una línea recta está determinada por solo dos puntos, solo necesitamos encontrar dos soluciones a la ecuación (aunque un tercer punto es útil como comprobación).
Intercepta
Cuando se da una ecuación lineal en dos variables en general desde,ax+by=c, a menudo los dos puntos más convenientes (soluciones) a fino se llaman Interceptos: estos son los puntos en los que la línea intercepta los ejes de coordenadas. Por supuesto, una línea horizontal o vertical intercepta solo un eje, por lo que este método no aplica. Las líneas horizontales y verticales se reconocen fácilmente ya que contienen solo una variable. (Ver Conjunto de Muestras C.)
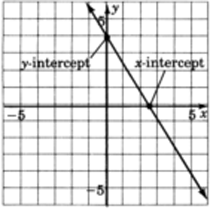
y-Interceptar
El punto en el que la línea cruza ely eje -se llama la y-intercepción. Elx -valor en este punto es cero (ya que el punto no está ni a la izquierda ni a la derecha del origen).
x-Interceptar
El punto en el que la línea cruza elx eje -se llama\(x\) -intercept y ely -value en ese punto es cero. Lay -intercepción se puede encontrar sustituyendo el valor0 parax en la ecuación y resolviendo paray. Lax -intercepción se puede encontrar sustituyendo el valor0 paray en la ecuación y resolviendo parax.
Método de intercepción
Como estamos graficando una ecuación al encontrar las intercepciones, llamamos a este método el método de intercepción
Conjunto de Muestras A
Grafica las siguientes ecuaciones usando el método de intercepción.
y−2x=−3
Para encontrar lay -intercepción, vamosx=0 yy=b.
\ (\ begin {alineado}
b - 2 (0) &=-3\\
b-0&=-3\\
b&=-3
\ end {alineado}\)
Así, tenemos el punto(0,3). Entonces six=0,y=b=−3.
Para encontrar lax -intercepción, vamosy=0 yx=a.
\ (\ begin {alineado}
0-2a&=-3\\
-2a&=-3&\ text {Dividir por} -2\\
a&=\ dfrac {-3} {-2}\\
a&=\ dfrac {3} {2}
\ end {alineado}\)
Así, tenemos el punto(32,0). Entonces, six=a=32,y=0.
Construye un sistema de coordenadas, traza estos dos puntos y dibuja una línea a través de ellos. Hay que tener en cuenta que cada punto de esta línea es una solución a la ecuacióny−2x=−3.
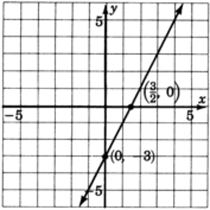
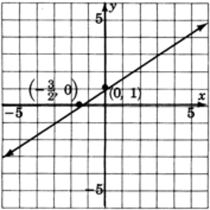
−2x+3y=3
Para encontrar lay -intercepción, vamosx=0 yy=b.
\ (\ begin {alineado}
-2 (0) + 3b&=3\\
0 + 3b&=3\\
3b&=3\\ b&=3\\
b&=1
\ end {alineado}\)
Así, tenemos el punto(0,1). Entonces, six=0,y=b=1.
Para encontrar lax -intercepción, vamosy=0 yx=a.
\ (\ begin {alineado}
-2a + 3 (0) &=3\\
-2a+0&=3\\
-2a&=3\\
a&=\ dfrac {3} {-2}\\
a&=-\ dfrac {3} {2}
\ end {alineado}\)
Así, tenemos el punto(−32,0). Entonces, six=a=−32,y=0.
Construye un sistema de coordenadas, traza estos dos puntos y dibuja una línea a través de ellos. Tenga en cuenta que todas las soluciones a la ecuación−2x+3y=3 están precisamente en esta línea.
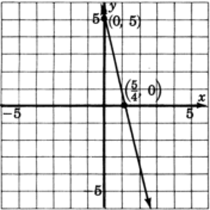
4x+y=5
Para encontrar lay -intercepción, vamosx=0 yy=b.
\ (\ begin {alineado}
4 (0) + b&=5\\
0+b&=5\\
b&=5
\ end {alineado}\)
Así, tenemos el punto(0,5). Entonces, six=0,y=b=5.
Para encontrar lax -intercepción, vamosy=0 yx=a.
\ (\ comenzar {alineado}
4a+0&=5\\
4a&=5\\
a&=\ dfrac {5} {4}
\ final {alineado}\)
Construye un sistema de coordenadas, traza estos dos puntos y dibuja una línea a través de ellos.
Conjunto de práctica A
Gráfica3x+y=3 usando el método de intercepción.
- Contestar
-
Cuandox=0,y=3; cuandoy=0,x=1
Graficar usando dos o más puntos cualesquiera
Las gráficas que hemos construido hasta ahora se han hecho encontrando dos puntos particulares, los interceptos. En realidad, dos puntos cualesquiera servirán. Elegimos usar las intercepciones porque suelen ser las más fáciles de trabajar con ellas. En el siguiente ejemplo, vamos a graficar dos ecuaciones usando puntos distintos a las intercepciones. Usaremos tres puntos, el punto extra que sirve como cheque.
Conjunto de Muestras B
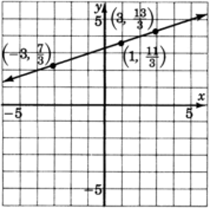
x−3y=−10
Podemos encontrar tres puntos eligiendo tresx -valores y calculando para encontrar losy -valores correspondientes. Pondremos nuestros resultados en una tabla para facilitar la lectura.
Ya que vamos a elegirx -valores y luego computar para encontrar losy -valores correspondientes, será para nuestra ventaja resolver la ecuación dada paray.
\ (\ begin {alineado}
x-3y&=-10&\ text {Restar} x\ texto {de ambos lados.} \\
-3y&=-x-10&\ text {Divide ambos lados por} -3\
y&=\ dfrac {1} {3} x +\ dfrac {10} {3}
\ end {alineado}\)
| x | y | (x,y) |
| 1 | Six=1, entoncesy=13(1)+103=13+103=113 | (1,113) |
| −3 | Six=−3, entoncesy=13(−3)+103=−1+103=73 | (−3,73) |
| 3 | Six=3, entoncesy=13(3)+103=1+103=133 | (3,133) |
Así, tenemos los tres pares ordenados (puntos),(1,113),(−3,73),(3,133). Si lo deseamos, podemos cambiar las fracciones impropias a números mixtos. (1,323),(−3,213),(3,413).
4x+4y=0
Resolvemos paray.
\ (4y = -4x\\
y = -x\)
| x | y | (x,y) |
| 0 | 0 | (0,0) |
| 2 | −2 | (2,−2) |
| −3 | 3 | (−3,3) |
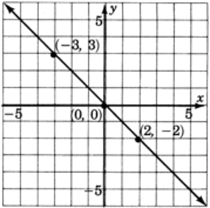
Observe que lasy intercepcionesx y son el mismo punto. Por lo tanto, el método de intercepción no proporciona suficiente información para construir esta gráfica.
Cuando se da una ecuación en la forma generalax+by=c, generalmente el enfoque más eficiente para construir la gráfica es usar el método de intercepción, cuando funciona.
Set de práctica B
Grafica las siguientes ecuaciones.
x−5y=5

- Contestar
-
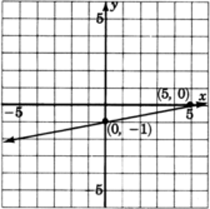
x+2y=6

- Contestar
-
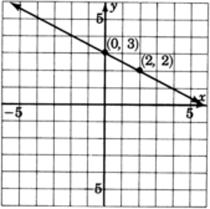
2x+y=1

- Contestar
-
Una gráfica de una línea que pasa por dos puntos con coordenadas cero, uno y uno, uno negativo.
Líneas inclinadas, horizontales y verticales
En todas las gráficas que hemos observado hasta el momento, las líneas han sido inclinadas. Este siempre será el caso cuando ambas variables aparezcan en la ecuación. Si solo aparece una variable en la ecuación, entonces la línea será vertical u horizontal. Para ver por qué, consideremos un caso específico:
Usando la forma general de una líneaax+by=c,, podemos producir una ecuación con exactamente una variable eligiendoa=0,b=5, yc=15. La ecuaciónax+by=c entonces se convierte en
0x+5y=15
Ya que0⋅(Any Number)=0, el término0x es0 para cualquier número que se elija parax.
Por lo tanto,
0x+5y=15
se convierte0+5y=15.
Pero,0 es la identidad aditiva y0+5y=5y.
5y=15.
Entonces, resolviendo paray obtenemos:
y=3
Esta es una ecuación en la que aparece exactamente una variable.
Esto significa que independientemente del número que elijamosx, ely valor -correspondiente es3. Dado que ely -valor es siempre el mismo a medida que nos movemos de izquierda a derecha a través de losx -valores, la altura de la línea por encimax del eje -siempre es la misma (en este caso, 3 unidades). Este tipo de línea debe ser horizontal.
Un argumento similar al anterior mostrará que si la única variable que aparece esx, podemos esperar obtener una línea vertical.
Conjunto de Muestras C
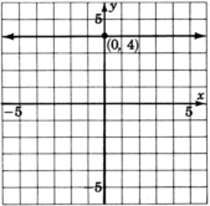
Gráficay=4.
La única variable que aparece esy. Independientemente delx -valor que elijamos, ely -valor es siempre4. Todos los puntos con uny -valor de4 satisfacer la ecuación. Así obtenemos una4 unidad de línea horizontal por encima delx eje -eje.
| x | y | (x, y) |
| −3 | 4 | (−3, 4) |
| −2 | 4 | (−2, 4) |
| −1 | 4 | (−1, 4) |
| 0 | 4 | (0, 4) |
| 1 | 4 | (1, 4) |
| 2 | 4 | (2, 4) |
| 3 | 4 | (3, 4) |
| 4 | 4 | (4, 4) |
Gráficax=−2.
La única variable que aparece esx. Independientemente dely -valor que elijamos, elx -valor siempre lo será−2. Así, obtenemos una línea vertical dos unidades a la izquierda dely eje -eje.
| x | y | (x,y) |
| −2 | −4 | (−2, −4) |
| −2 | −3 | (−2, −3) |
| −2 | −2 | (−2, −2) |
| −2 | −1 | (−2, −1) |
| −2 | 0 | (−2, 0) |
| −2 | 1 | (−2, 1) |
| −2 | 2 | (−2, 0) |
| −2 | 3 | (−2, 3) |
| −2 | 4 | (−2, 4) |
Set de práctica C
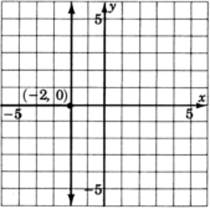
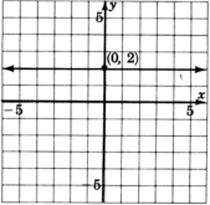
Gráficay=2.

- Contestar
-
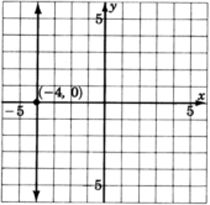
Gráficax=−4.

- Contestar
-
Resumiendo nuestros resultados podemos hacer las siguientes observaciones:
- Cuando una ecuación lineal en dos variables se escribe en la formaax+by=c, decimos que está escrita en forma general.
- Para graficar una ecuación en forma general a veces es conveniente utilizar el método de intercepción.
- Una ecuación lineal en la que aparecen ambas variables se graficará como una línea inclinada.
- Una ecuación lineal en la que solo aparece una variable se graficará como una línea vertical u horizontal.
x=agráficas como una línea vertical quea pasa por elx eje.
y=bgráficas como una línea horizontal queb pasa por ely eje.
Ejercicios
Para los siguientes problemas, grafica las ecuaciones.
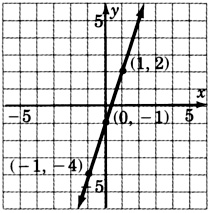
−3x+y=−1

- Contestar
-
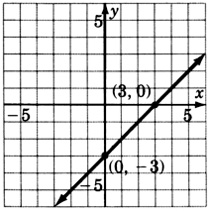
3x−2y=6

−2x+y=4
- Contestar
-
x−3y=5

2x−3y=6

- Contestar
-
2x+5y=10

3(x−y)=9

- Contestar
-
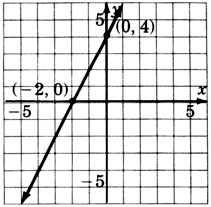
−2x+3y=−12

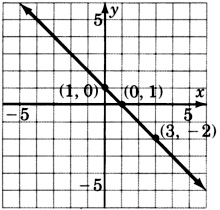
y+x=1

- Contestar
-
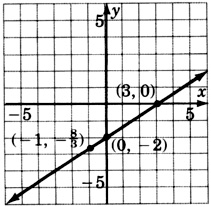
4y−x−12=0

2x−y+4=0

- Contestar
-
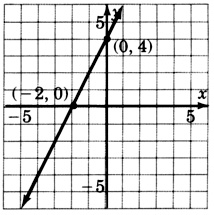
−2x+5y=0

y−5x+4=0

- Contestar
-
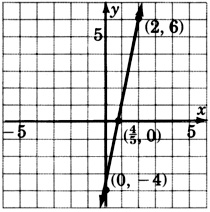
0x+y=3

0x+2y=2

- Contestar
-
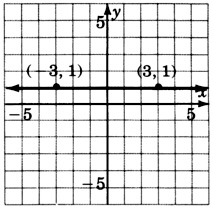
0x+14y=1

4x+0y=16

- Contestar
-
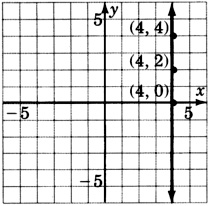
12x+0y=−1

23x+0y=1

- Contestar
-
x=32
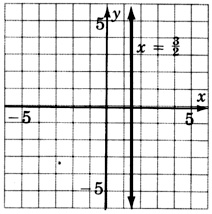
y=3

y=−2

- Contestar
-
y=−2
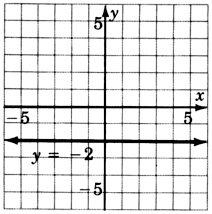
−4y=20

x=−4

- Contestar
-
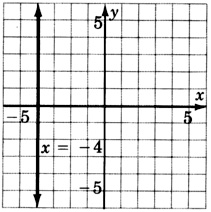
−3x=−9

−x+4=0

- Contestar
-
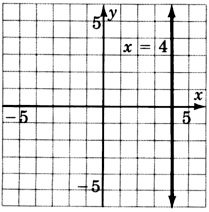
Construir la gráfica de todos los puntos que tienen coordenadas(a, a), es decir, para cada punto, losy valoresx y son los mismos.

2.53x+4.77y=8.45

- Contestar
-
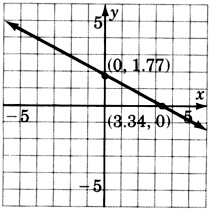
1.96x+2.05y=6.55

4.1x−6.6y=15.5

- Contestar
-
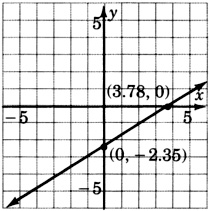
626.01x−506.73y=2443.50

Ejercicios para la revisión
Nombra la propiedad de números reales que haga4+x=x+4 una declaración verdadera.
- Contestar
-
propiedad conmutativa de adición
Suministrar la palabra faltante. El valor absoluto de un númeroa, denotado|a|, es el dea a0 en la recta numérica.
Encuentra el producto(3x+2)(x−7).
- Contestar
-
3x2−19x−14
Resolver la ecuación3[3(x−2)+4x]−24=0
Suministrar la palabra faltante. Los ejes de coordenadas dividen el plano en cuatro regiones iguales llamadas.
- Contestar
-
cuadrantes


