Inicio
Matemáticas
Álgebra
Álgebra inicial
3: Graficar líneas
3.8: Desigualdades lineales (dos variables)

3.8: Desigualdades lineales (dos variables)

Última actualización
Guardar como PDF

Page ID: 110106

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Identificar y verificar soluciones a desigualdades lineales con dos variables.
Gráfica conjuntos de soluciones de desigualdades lineales con dos variables.

Soluciones a Desigualdades Lineales

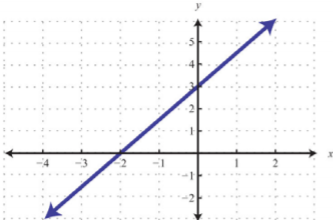
Sabemos que una ecuación lineal con dos variables tiene infinitamente muchas soluciones de pares ordenados que forman una línea cuando se grafican. Una desigualdad lineal con dos variables, por otro lado, tiene un conjunto de soluciones que consiste en una región que define la mitad del plano.

Mesa$\PageIndex{1}$
Ecuación Lineal	Desigualdad Lineal
$y=\frac{3}{2}x+3$	$y\leq \frac{3}{2}x+3$
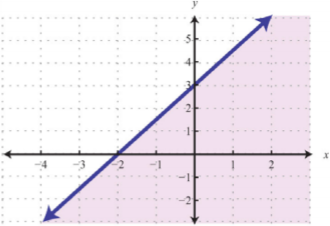
$Captura de pantalla (681) .png$ *Figura$\PageIndex{1}$*	$Captura de pantalla (682) .png$ *Figura$\PageIndex{2}$*

Para la desigualdad, la línea define un límite de la región que está sombreada. Esto indica que cualquier par ordenado que se encuentre en la región sombreada, incluida la línea límite, satisfará la desigualdad. Para ver que este es el caso, elija algunos puntos de prueba y sustituirlos por la desigualdad.

Mesa$\PageIndex{2}$
$\color{Cerulean}{Test\:point}$	$y\leq\frac{3}{2}x+3$
$(0,0)$	$\begin{aligned} 0&\leq \frac{3}{2}(0)+3 \\ 0&\leq 3 \quad\color{Cerulean}{\checkmark} \end{aligned}$
$(2,1)$	$\begin{aligned} 1&\leq \frac{3}{2}(2)+3 \\ 1&\leq 3+3 \\ 1&\leq 6\quad\color{Cerulean}{\checkmark}\end{aligned}$
$(-2,-1)$	$\begin{aligned} -1&\leq\frac{3}{2}(-2)+3 \\ -1&\leq -3+3 \\ -1&\leq 0\quad\color{Cerulean}{\checkmark} \end{aligned}$

También, podemos ver que los pares ordenados fuera de la región sombreada no resuelven la desigualdad lineal.

$\begin{array} {c|c} {\underline{\color{Cerulean}{Test\:point}}}&{\underline{y\leq\frac{3}{2}x+3}}\\{(-2,3)} &{3\leq\frac{3}{2}(-2)+3}\\{}&{3\leq -3+3}\\{}&{3\leq 0\quad\color{red}{x}} \end{array}$

La gráfica de la solución establecida en una desigualdad lineal es siempre una región. Sin embargo, es posible que el límite no siempre esté incluido en ese conjunto. En el ejemplo anterior, la línea formaba parte del conjunto de soluciones por la parte “o igual a” de la desigualdad inclusiva$≤$. Si tenemos una desigualdad estricta$<$, entonces usaríamos una línea discontinua para indicar que esos puntos no están incluidos en el conjunto de soluciones.

Mesa$\PageIndex{3}$
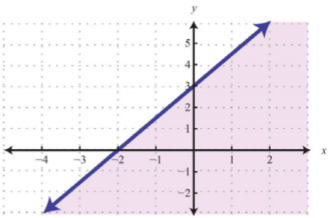
Límite no inclusivo	Límite Inclusivo
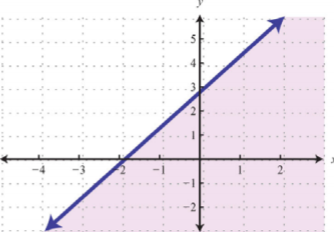
$y<\frac{3}{2}x+3$	$y\leq \frac{3}{2}x+3$
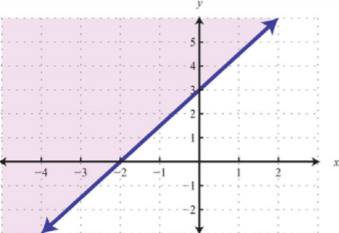
$Captura de pantalla (683) .png$ *Figura$\PageIndex{3}$*	$Captura de pantalla (684) .png$ *Figura$\PageIndex{4}$*

Considera el punto$(0, 3)$ en el límite; este par ordenado satisface la ecuación lineal. Es la parte “o igual a” de la desigualdad inclusiva la que la hace parte del conjunto de soluciones.

$\begin{array}{c|c}{\underline{y<\frac{3}{2}x+3}}&{\underline{y\leq \frac{3}{2}x+3}}\\{3<\frac{3}{2}(0)+3}&{3\leq\frac{3}{2}(0)+3}\\{3<0+3}&{3\leq 0+3}\\{3<3\quad\color{red}{x}}&{3\leq 3\quad\color{Cerulean}{\checkmark}} \end{array}$

Hasta el momento, hemos visto ejemplos de desigualdades que eran “menores que”. Ahora considere las siguientes gráficas con el mismo límite:

Mesa$\PageIndex{4}$
Mayor que (arriba)	Menos que (Abajo)
$y\geq \frac{3}{2}x+3$	$y\leq \frac{3}{2}x+3$
$Captura de pantalla (685) .png$ *Figura$\PageIndex{5}$*	$Captura de pantalla (686) .png$ *Figura$\PageIndex{6}$*

Dadas las gráficas anteriores, ¿qué podríamos esperar si usamos el origen$(0, 0)$ como punto de prueba?

$\begin{array}{c|c}{\underline{y\geq\frac{3}{2}x+3}}&{\underline{y\leq\frac{3}{2}x+3}}\\{0\geq\frac{3}{2}(0)+3}&{0\leq\frac{3}{2}(0)+3}\\{0\geq 0+3}&{0\leq0+3}\\{0\geq 3\quad\color{red}{x}}&{0\leq 3\quad\color{Cerulean}{\checkmark}} \end{array}$

Ejercicio$\PageIndex{1}$

¿Cuál de los pares ordenados$(−2, −1), (0, 0), (−2, 8), (2, 1),$ y$(4, 2)$ resuelve la desigualdad$y>−\frac{1}{2}x+2$?

Contestar: $(−2, 8)$y$(4, 2)$

Graficando Soluciones a Desigualdades Lineales

Las soluciones a las desigualdades lineales son un semiplano sombreado, delimitado por una línea continua o una línea discontinua. Este límite se incluye en la solución o no, dependiendo de la desigualdad dada. Si se nos da una desigualdad estricta, utilizamos una línea discontinua para indicar que el límite no está incluido. Si se nos da una desigualdad inclusiva, utilizamos una línea sólida para indicar que está incluida. Los pasos para graficar el conjunto de soluciones para una desigualdad con dos variables se describen en el siguiente ejemplo.

Ejemplo$\PageIndex{1}$

Grafique el conjunto de soluciones:

$y>−3x+1$.

Solución:

Paso 1: Grafica la línea límite. En este caso, grafica una línea discontinua$y=−3x+1$ debido a la estricta desigualdad. Por inspección, vemos que la pendiente es$m=−3=−\frac{3}{1}=\frac{rise}{run}$ y la$y$ -intercepción es$(0, 1)$.

$Captura de pantalla (687) .png$

Figura$\PageIndex{7}$

Paso 2: Pruebe un punto que no esté en el límite. Un punto de prueba común es el origen$(0, 0)$. El punto de prueba nos ayuda a determinar qué mitad del avión sombrear.

$\begin{array}{c|c} {\underline{\color{Cerulean}{Test\:point}}}&{\underline{y>-3x+1}}\\{(0,0)}&{0>-3(0)+1}\\{}&{0>1\quad\color{red}{x}} \end{array}$

Paso 3: Sombra la región que contiene las soluciones. Dado que el punto de prueba no$(0, 0)$ fue una solución, no se encuentra en la región que contiene todas las soluciones de pares ordenadas. Por lo tanto, sombree la mitad del plano que no contiene este punto de prueba. En este caso, sombrea por encima de la línea límite.

Respuesta:

$Captura de pantalla (688) .png$

Figura$\PageIndex{8}$

Considera el problema del sombreado por encima o por debajo de la línea límite cuando la desigualdad está en forma de pendiente-intercepción. Si$y>mx+b$, entonces sombra por encima de la línea. Si$y<mx+b$, entonces sombra por debajo de la línea. Use esto con precaución; a veces el límite se da en forma estándar, en cuyo caso estas reglas no aplican.

Ejemplo$\PageIndex{2}$

Grafique el conjunto de soluciones:

$2x−5y≥−10$.

Solución:

Aquí el límite está definido por la línea$2x−5y=−10$. Dado que la desigualdad es inclusiva, graficamos el límite usando una línea continua. En este caso, grafica la línea límite usando intercepciones.

$Captura de pantalla (689) .png$

Figura$\PageIndex{9}$

A continuación, pruebe un punto; esto ayuda a decidir a qué región sombrear.

$\begin{array} {c|c} {\underline{\color{Cerulean}{Test\:point}}}&{\underline{2x-5y\geq -10}}\\{(0,0)}&{2(0)-5(0)\geq -10} \\ {}&{0\geq -10\quad\color{Cerulean}{\checkmark}} \end{array}$

Dado que el punto de prueba está en el conjunto de soluciones, sombree la mitad del plano que lo contiene.

Respuesta:

$Captura de pantalla (690) .png$

Figura$\PageIndex{10}$

En este ejemplo, observe que el conjunto de soluciones consiste en todos los pares ordenados por debajo de la línea límite. Esto puede ser contrario a la intuición por lo original$≥$ en la desigualdad. Esto ilustra que es una buena práctica probar realmente un punto. Resuelve para$y$ y ves que el sombreado es correcto.

En forma de pendiente-intercepción, puede ver que la región debajo de la línea de límite debe estar sombreada. Un enfoque alternativo es expresar primero el límite en forma de pendiente-intercepción, graficarlo y luego sombrear la región apropiada.

Ejemplo$\PageIndex{3}$

Grafique el conjunto de soluciones:

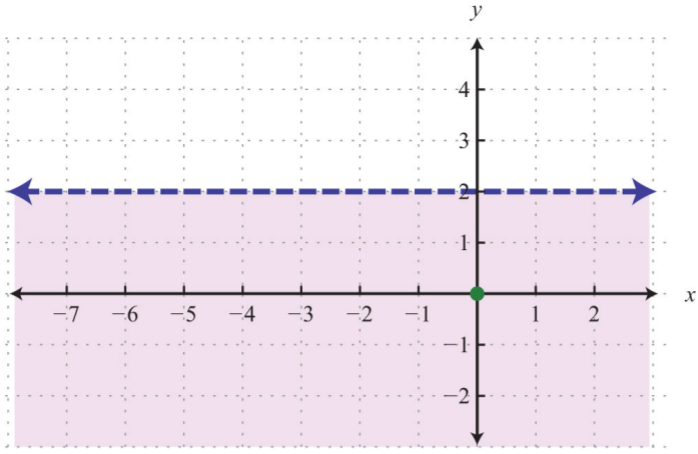
$y<2$.

Solución:

Primero, grafica la línea límite$y=2$ con una línea discontinua debido a la estricta desigualdad.

$Captura de pantalla (691) .png$

Figura$\PageIndex{11}$

Ahora, prueba un punto.

$\begin{array}{c|c}{\underline{\color{Cerulean}{Test\:point}}}&{\underline{y<2}}\\{(0,0)}&{0<2\quad\color{Cerulean}{\checkmark}} \end{array}$

En este caso, sombree la región que contiene el punto de prueba.

Respuesta:

$Captura de pantalla (692) .png$

Figura$\PageIndex{12}$

Ejercicio$\PageIndex{2}$

Grafique el conjunto de soluciones:

$5x−y≤10$.

Contestar

$Captura de pantalla (693) .png$

Figura$\PageIndex{13}$

Claves para llevar

Las desigualdades lineales con dos variables tienen infinitamente muchas soluciones de pares ordenados, que se pueden graficar sombreando en la mitad apropiada de un plano de coordenadas rectangulares.
Para graficar el conjunto de soluciones de una desigualdad lineal con dos variables, primero graficar el límite con una línea discontinua o continua dependiendo de la desigualdad. Si se le da una desigualdad estricta, use una línea discontinua para el límite. Si se le da una desigualdad inclusiva, use una línea sólida. A continuación, elija un punto de prueba que no esté en el límite. Si el punto de prueba resuelve la desigualdad, entonces sombrea la región que lo contiene; de lo contrario, sombree el lado opuesto.
Al graficar los conjuntos de soluciones de desigualdades lineales, es una buena práctica probar valores dentro y fuera del conjunto de soluciones como una comprobación.

Ejercicio$\PageIndex{3}$ Solutions to Linear Inequalities (Two Variables)

¿El par ordenado es una solución a la desigualdad dada?

$y<5x+1$;$(0,0)$
$y>−\frac{1}{2}x−4$;$(0, −2)$
$y≤\frac{2}{3}x+1$;$(6, 5)$
$y≥−\frac{1}{3}x−5$;$(−3, −8)$
$y<\frac{1}{5}x-\frac{1}{3}$;$(-\frac{1}{2},-1)$
$4x-3y\leq 2$;$(-2,-1)$
$-x+4y>7$;$(0, 0)$
$7x−3y<21$;$(5,-3)$
$y>−5$;$(−3, −1)$
$x≤0$;$(0, 7)$

Contestar

1. Sí

3. Sí

5. Sí

7. No

9. Sí

Ejercicio$\PageIndex{4}$ Graphing Solutions to Linear Inequalities

Grafique el conjunto de soluciones.

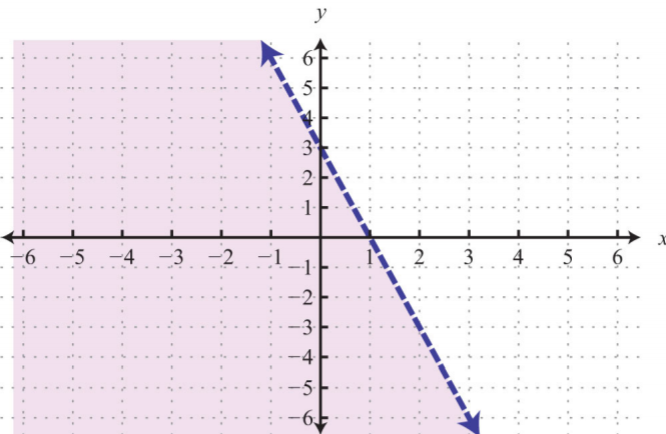
$y<−3x+3$
$y<−\frac{2}{3}x+4$
$y≥−\frac{1}{2}x$
$y≥\frac{4}{5}x−8$
$y≤8x−7$
$y>−5x+3$
$y>−x+4$
$y>x−2$
$y≥−1$
$y<−3$
$x<2$
$x≥2$
$y≤\frac{3}{4}x−\frac{1}{2}$
$y>−\frac{3}{2}x+\frac{5}{2}$
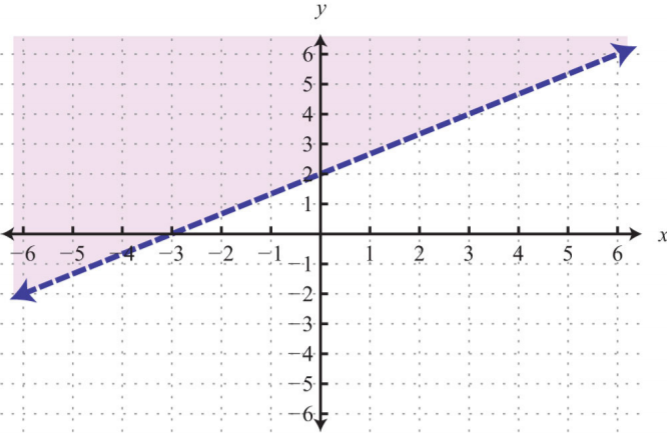
$−2x+3y>6$
$7x−2y>14$
$5x−y<10$
$x-y<0$
$3x−2y≥0$
$x−5y≤0$
$−x+2y≤−4$
$−x+2y≤3$
$2x−3y≥−1$
$5x−4y<−3$
$\frac{1}{2}x-\frac{1}{3}y<1$
$\frac{1}{2}x-\frac{1}{10}y\geq\frac{1}{2}$
$x≥−2y$
$x<2y+3$
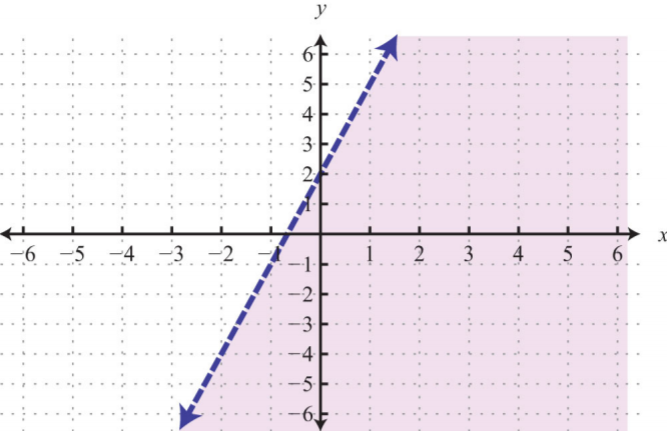
$3x−y+2>0$
$3−y−2x<0$
$−4x≤12−3y$
$5x≤−4y−12$
Escribe una desigualdad que describa todos los puntos en el medio plano superior por encima del$x$ eje.
Escribe una desigualdad que describa todos los puntos en el medio plano inferior debajo del$x$ eje.
Escribe una desigualdad que describa todos los puntos en el medio plano izquierdo del$y$ eje.
Escribe una desigualdad que describa todos los puntos en el medio plano derecho del$y$ eje.
Escribe una desigualdad que describa todos los pares ordenados cuyas$y$ coordenadas son al menos$2$.
Escribe una desigualdad que describa todos los pares ordenados cuya$x$ coordenada es como mucho$5$.

Contestar

$Captura de pantalla (694) .png$

Figura$\PageIndex{14}$

$Captura de pantalla (695) .png$

Figura$\PageIndex{15}$

$Captura de pantalla (696) .png$

Figura$\PageIndex{16}$

$Captura de pantalla (697) .png$

Figura$\PageIndex{17}$

$Captura de pantalla (698) .png$

Figura$\PageIndex{18}$

11.

$Captura de pantalla (699) .png$

Figura$\PageIndex{19}$

13.

$Captura de pantalla (700) .png$

Figura$\PageIndex{20}$

15.

$Captura de pantalla (701) .png$

Figura$\PageIndex{21}$

17.

$Captura de pantalla (702) .png$

Figura$\PageIndex{22}$

19.

$Captura de pantalla (703) .png$

Figura$\PageIndex{23}$

21.

$Captura de pantalla (704) .png$

Figura$\PageIndex{24}$

23.

$Captura de pantalla (705) .png$

Figura$\PageIndex{25}$

25.

$Captura de pantalla (706) .png$

Figura$\PageIndex{26}$

27.

$Captura de pantalla (707) .png$

Figura$\PageIndex{27}$

29.

$Captura de pantalla (708) .png$

Figura$\PageIndex{28}$

31.

$Captura de pantalla (709) .png$

Figura$\PageIndex{29}$

33. $y>0$

35. $x<0$

37. $y≥2$

Ecuación Lineal	Desigualdad Lineal
\(y=\frac{3}{2}x+3\)	\(y\leq \frac{3}{2}x+3\)
$Captura de pantalla (681) .png$ *Figura\(\PageIndex{1}\)*	$Captura de pantalla (682) .png$ *Figura\(\PageIndex{2}\)*

\(\color{Cerulean}{Test\:point}\)	\(y\leq\frac{3}{2}x+3\)
\((0,0)\)	\(\begin{aligned} 0&\leq \frac{3}{2}(0)+3 \\ 0&\leq 3 \quad\color{Cerulean}{\checkmark} \end{aligned}\)
\((2,1)\)	\(\begin{aligned} 1&\leq \frac{3}{2}(2)+3 \\ 1&\leq 3+3 \\ 1&\leq 6\quad\color{Cerulean}{\checkmark}\end{aligned}\)
\((-2,-1)\)	\(\begin{aligned} -1&\leq\frac{3}{2}(-2)+3 \\ -1&\leq -3+3 \\ -1&\leq 0\quad\color{Cerulean}{\checkmark} \end{aligned}\)

Límite no inclusivo	Límite Inclusivo
\(y<\frac{3}{2}x+3\)	\(y\leq \frac{3}{2}x+3\)
$Captura de pantalla (683) .png$ *Figura\(\PageIndex{3}\)*	$Captura de pantalla (684) .png$ *Figura\(\PageIndex{4}\)*

Mayor que (arriba)	Menos que (Abajo)
\(y\geq \frac{3}{2}x+3\)	\(y\leq \frac{3}{2}x+3\)
$Captura de pantalla (685) .png$ *Figura\(\PageIndex{5}\)*	$Captura de pantalla (686) .png$ *Figura\(\PageIndex{6}\)*

Search

Text Color

Text Size

Margin Size

Font Type