4.1: Resolver sistemas lineales mediante gráficos
- Page ID
- 110149
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Verificar soluciones a sistemas de ecuaciones lineales.
- Resolver sistemas lineales utilizando el método de graficación.
- Identificar sistemas dependientes e inconsistentes.
Definición de un Sistema Lineal
Las aplicaciones del mundo real a menudo se modelan usando más de una variable y más de una ecuación. Un sistema de ecuaciones consiste en un conjunto de dos o más ecuaciones con las mismas variables. En esta sección, estudiaremos sistemas lineales consistentes en dos ecuaciones lineales cada una con dos variables. Por ejemplo,
Una solución a un sistema lineal, o solución simultánea, a un sistema lineal es un par ordenado\((x, y)\) que resuelve ambas ecuaciones. En este caso,\((3, 2)\) es la única solución. Para verificar que un par ordenado es una solución, sustituya los\(y\) valores\(x\) -y -correspondientes en cada ecuación y luego simplifique para ver si obtiene una declaración verdadera para ambas ecuaciones.
\(\color{Cerulean}{Check:}\:\color{black}{(3,2)}\)
\(\begin{array} {c|c}{Equation\:1:\:\:2x-37=0}&{Equation\:2\:\:-4x+2y=-8}\\{2(\color{OliveGreen}{3}\color{black}{)-3(}\color{OliveGreen}{2}\color{black}{)=0}}&{-4(\color{OliveGreen}{3}\color{black}{)+2(}\color{OliveGreen}{2}\color{black}{)=-8}}\\{6-6=0}&{-12+4=-8}\\{0=0\quad\color{Cerulean}{\checkmark}}&{-8=-8\quad\color{Cerulean}{\checkmark}} \end{array}\)
Ejemplo\(\PageIndex{1}\)
Determinar si\((1, 0)\) es una solución para el sistema
\(\left\{\begin{aligned} x−y&=1 \\ −2x+3y&=5 \end{aligned}\right.\).
Solución:
Sustituir los valores apropiados en ambas ecuaciones.
\(\color{Cerulean}{Check:}\:\color{black}{(1,0)}\)
\(\begin{array}{c|c} {Equation\:1:\:\:x-y=1}&{Equation\:2:\:\:-2x+3y=5}\\{(\color{OliveGreen}{1}\color{black}{)-(}\color{OliveGreen}{0}\color{black}{)=1}}&{-2(\color{OliveGreen}{1}\color{black}{)+3(}\color{OliveGreen}{0}\color{black}{)=5}}\\{1-0=1}&{-2+0=5}\\{1=1\quad\color{Cerulean}{\checkmark}}&{-2=5\quad\color{red}{x}} \end{array}\)
Respuesta:
Dado que\((1, 0)\) no satisface ambas ecuaciones, no es una solución.
Ejercicio\(\PageIndex{1}\)
Es\((−2, 4)\) una solución al sistema
\(\begin{aligned} x−y&=−6\\−2x+3y&=16\end{aligned}\)?
- Contestar
-
Sí
Resolver graficando
Geométricamente, un sistema lineal consta de dos líneas, donde una solución es un punto de intersección. Para ilustrar esto, graficaremos el siguiente sistema lineal con una solución de\((3, 2)\):
Primero, reescribir las ecuaciones en forma de pendiente-intersección para que podamos graficarlas fácilmente.
\(\begin{array}{c|c}{2x-3y=0}&{-4x+2y=-8}\\{2x-3y\color{Cerulean}{-2x}\color{black}{=0}\color{Cerulean}{-2x}}&{-4x+2y\color{Cerulean}{+4x}\color{black}{=-8}\color{Cerulean}{+4x}}\\{-3y=-2x}&{2y=4x-8}\\{\frac{-3y}{\color{Cerulean}{-3}}\color{black}{=\frac{-2x}{\color{Cerulean}{-3}}}}&{\frac{2y}{\color{Cerulean}{2}}\color{black}{=\frac{4x-8}{\color{Cerulean}{2}}}}\\{y=\frac{2}{3}x}&{y=2x-4} \end{array}\)
A continuación, sustituir estas formas de las ecuaciones originales en el sistema para obtener lo que se llama un sistema equivalente. Los sistemas equivalentes comparten el mismo conjunto de soluciones.
\(\color{Cerulean}{Original\:system}\qquad\color{Cerulean}{Equivalent\:system}\)
Si graficamos ambas líneas en un mismo conjunto de ejes, entonces podemos ver que el punto de intersección es efectivamente\((3, 2)\), la solución al sistema.
Para resumir, los sistemas lineales descritos en esta sección consisten en dos ecuaciones lineales cada una con dos variables. Una solución es un par ordenado que corresponde a un punto donde se cruzan las dos líneas en el plano de coordenadas rectangulares. Por lo tanto, podemos resolver sistemas lineales graficando ambas líneas en un mismo conjunto de ejes y determinando el punto donde se cruzan. Al graficar las líneas, tenga cuidado de elegir una buena escala y use una recta para dibujar la línea a través de los puntos; la precisión es muy importante aquí. Los pasos para resolver sistemas lineales utilizando el método de graficación se describen en el siguiente ejemplo.
Ejemplo\(\PageIndex{2}\)
Resuelve graficando:
\(\left\{\begin{aligned} x−y&=−4 \\2x+y&=1\end{aligned}\right.\).
Solución:
Paso 1: Reescribir las ecuaciones lineales en forma de pendiente-intersección.
\(\begin{array}{c|c}{x-y=-4}&{2x+y=1}\\{x-y\color{Cerulean}{-x}\color{black}{=-4}\color{Cerulean}{-x}}&{2x+y\color{Cerulean}{-2x}\color{black}{=1}\color{Cerulean}{-2x}}\\{-y=-x-4}&{y=-2x+1}\\{\frac{-y}{\color{Cerulean}{-1}}\color{black}{=\frac{-x-4}{\color{Cerulean}{-1}}}}&{}\\{y=x+4}&{} \end{array}\)
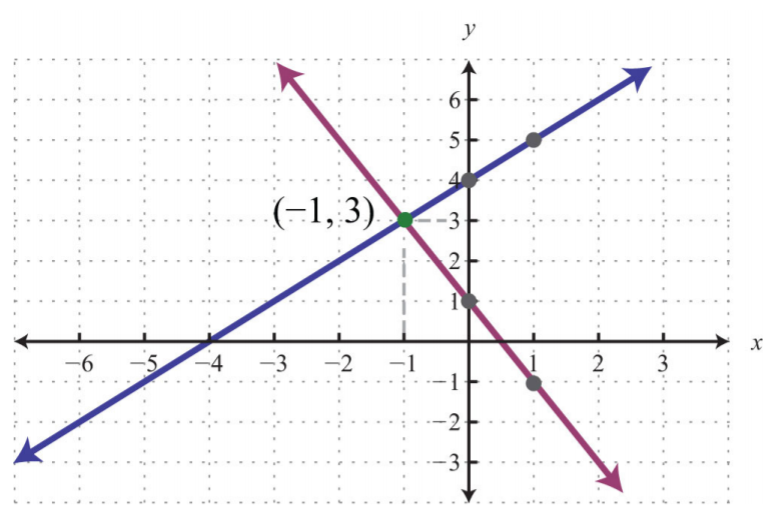
Paso 2: Escribe el sistema equivalente y grafica las líneas en el mismo conjunto de ejes.
\(\begin{array}{c|c} {\color{Cerulean}{Line\:1:}\:\color{black}{y=x+4}}&{\color{Cerulean}{Line\:2}\:\color{black}{y=-2x+1}}\\{y-intercept:\:(0,4)}&{y-intercept:\:(0,1)}\\{slope:\:m=1=\frac{1}{1}=\frac{rise}{run}}&{slope:\:m=-2=\frac{-2}{1}=\frac{rise}{run}} \end{array}\)
.png)
Paso 3: Usa la gráfica para estimar el punto donde se cruzan las líneas y comprueba si resuelve el sistema original. En la gráfica anterior, el punto de intersección parece ser\((−1, 3)\).
\(\color{Cerulean}{Check:}\:\color{black}{(-1,3)}\)
\(\begin{array}{c|c} {Line\:1:\:\: x-y=-4}&{Line\:2:\:\: 2x+y=1}\\{(\color{OliveGreen}{-1}\color{black}{)-(}\color{OliveGreen}{3}\color{black}{)=-4}}&{2(\color{OliveGreen}{-1}\color{black}{)+(}\color{OliveGreen}{3}\color{black}{)=1}}\\{-1-3=-4}&{-2+3=1}\\{-4=-4\quad\color{Cerulean}{\checkmark}}&{1=1\quad\color{Cerulean}{\checkmark}} \end{array}\)
Respuesta:
\((-1,3)\)
Ejemplo\(\PageIndex{3}\)
Resuelve graficando:
\(\left\{\begin{aligned} 2x+y&=2\\−2x+3y&=−18 \end{aligned}\right.\).
Solución:
Primero resolvemos cada ecuación\(y\) para obtener un sistema equivalente donde las líneas están en forma de pendiente-intersección.
Grafica las líneas y determina el punto de intersección.
\(\color{Cerulean}{Check:}\:\:\color{black}{(3,-4)}\)
\(\begin{array} {c|c} {2x+y=2}&{-2x+3y=-18}\\{2(\color{OliveGreen}{3}\color{black}{)+(}\color{OliveGreen}{-4}\color{black}{)=2}}&{-2(\color{OliveGreen}{3}\color{black}{)+3(}\color{OliveGreen}{-4}\color{black}{)=-18}}\\{6-4=2}&{-6-12=-18}\\{2=2\quad\color{Cerulean}{\checkmark}}&{-18=-18\quad\color{Cerulean}{\checkmark}} \end{array}\)
Respuesta:
\((3,-4)\)
Ejemplo\(\PageIndex{4}\)
Resuelve graficando:
\(\left\{\begin{aligned} 3x+y&=6\\y&=−3 \end{aligned}\right.\)
Solución:
\(\color{Cerulean}{Check:}\:\color{black}{(3,-3)}\)
\(\begin{array}{c|c}{3x+y=6}&{y=-3}\\{3(\color{OliveGreen}{3}\color{black}{)+(}\color{OliveGreen}{-3}\color{black}{)=6}}&{(\color{OliveGreen}{-3}\color{black}{)=-3}}\\{9-3=6}&{-3=-3\quad\color{Cerulean}{\checkmark}}\\{6=6\quad\color{Cerulean}{\checkmark}}&{} \end{array}\)
Respuesta:
\((3,-3)\)
El método de graficación para resolver sistemas lineales no es ideal cuando la solución consiste en coordenadas que no son números enteros. Habrá métodos algebraicos más precisos en las secciones por venir, pero por ahora, el objetivo es entender la geometría involucrada a la hora de resolver sistemas. Es importante recordar que las soluciones a un sistema corresponden al punto, o puntos, donde se cruzan las gráficas de las ecuaciones.
Ejercicio\(\PageIndex{2}\)
Resuelve graficando:
\(\left\{\begin{aligned}−x+y&=6\\ 5x+2y&=−2 \end{aligned}\right.\).
- Contestar
-
\((-2,4)\)
Sistemas dependientes e inconsistentes
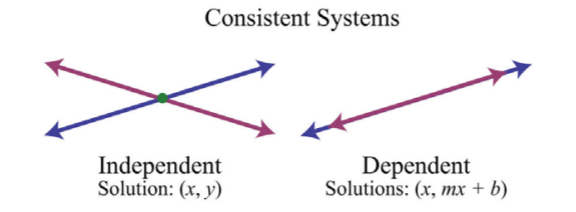
Los sistemas con al menos una solución se denominan sistemas consistentes. Hasta este punto, todos los ejemplos han sido de sistemas consistentes con exactamente una solución de par ordenado. Resulta que no siempre es así. En ocasiones los sistemas constan de dos ecuaciones lineales que son equivalentes. Si este es el caso, las dos líneas son iguales y cuando se grafican coincidirán. De ahí que el conjunto de soluciones consiste en todos los puntos de la línea. Este es un sistema dependiente. Dado un sistema lineal consistente con dos variables, hay dos resultados posibles:
.png)
Las soluciones a sistemas independientes son pares ordenados\((x, y)\). Necesitamos alguna forma de expresar los conjuntos de soluciones a sistemas dependientes, ya que estos sistemas tienen infinitamente muchas soluciones, o puntos de intersección. Recordemos que cualquier línea se puede escribir en forma de pendiente-intercepción,\(y=mx+b\). Aquí,\(y\) depende de\(x\). Por lo que podemos expresar todas las soluciones de par ordenadas\((x, y)\) en la forma\((x, mx+b)\), donde\(x\) está cualquier número real.
Ejemplo\(\PageIndex{5}\)
Resuelve graficando:
\(\left\{\begin{aligned}−2x+3y&=−9 \\ 4x−6y&=18\end{aligned}\right.\).
Solución:
Determinar la forma pendiente-intersección para cada ecuación lineal en el sistema.
\(\begin{array}{c|c} {-2x+3y=-9}&{4x-6y=18}\\{-2x+3y\color{Cerulean}{+2x}\color{black}{=-9}\color{Cerulean}{+2x}}&{4x-6y\color{Cerulean}{-4x}\color{black}{=18}\color{Cerulean}{-4x}}\\{3y=2x-9}&{-6y=-4x+18}\\{\frac{3y}{\color{Cerulean}{3}}\color{black}{=\frac{2x-9}{\color{Cerulean}{3}}}}&{\frac{-6y}{\color{Cerulean}{-6}}\color{black}{=\frac{-4x+18}{\color{Cerulean}{-6}}}}\\{y=\frac{2}{3}x-3}&{y=\frac{-4}{-6}x+\frac{18}{-6}}\\{}&{y=\frac{2}{3}x-3} \end{array}\)
En forma de pendiente-intercepción, podemos ver fácilmente que el sistema consta de dos líneas con la misma pendiente y la misma\(y\) intersección.
Son, de hecho, la misma línea. Y el sistema es dependiente.
Respuesta:
\((x,\frac{2}{3}x-3)\)
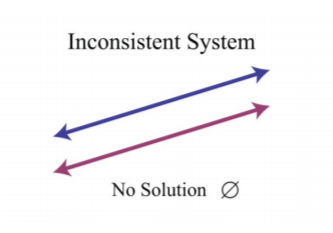
En este ejemplo, es importante notar que las dos líneas tienen la misma pendiente y la misma\(y\) intersección. Esto nos dice que las dos ecuaciones son equivalentes y que las soluciones simultáneas son todos los puntos en la línea\(y=\frac{2}{3}x−3\). Este es un sistema dependiente, y las infinitamente muchas soluciones se expresan usando la forma\((x, mx+b)\). Otros recursos pueden expresar este conjunto usando la notación de conjunto\(\{(x, y) | y=\frac{2}{3}x−3\}\), que dice “el conjunto de todos los pares ordenados de\((x, y)\) tal manera que\(y\) equivale a dos tercios\(x\) menos”\(3\). A veces las líneas no se cruzan y no hay punto de intersección. Tales sistemas no tienen solución,\(Ø\), y se denominan sistemas inconsistentes.
.png)
Ejemplo\(\PageIndex{6}\)
Resuelve graficando:
\(\left\{\begin{aligned}−2x+5y&=−15\\−4x+10y&=10\end{aligned}\right.\).
Solución:
Determinar la forma pendiente-intersección para cada ecuación lineal.
\(\begin{array}{c|c} {-2x+5y=-15}&{-4x+10y=10}\\{-2x+5y\color{Cerulean}{+2x}\color{black}{=-15}\color{Cerulean}{+2x}}&{-4x+10y\color{Cerulean}{+4x}\color{black}{=10}\color{Cerulean}{+4x}}\\{5y=2x-15}&{10y=4x+10}\\{\frac{5y}{\color{Cerulean}{5}}\color{black}{=\frac{2x-15}{\color{Cerulean}{5}}}}&{\frac{10y}{\color{Cerulean}{10}}\color{black}{=\frac{4x+10}{\color{Cerulean}{10}}}}\\{y=\frac{2}{5}x-3}&{y=\frac{2}{5}x+1} \end{array}\)
En forma de pendiente-intercepción, podemos ver fácilmente que el sistema consta de dos líneas con la misma pendiente y diferentes\(y\) -intercepciones.
Por lo tanto, son paralelos y nunca se cruzarán.
Respuesta:
No hay solución simultánea,\(Ø\).
Ejercicio\(\PageIndex{3}\)
Resuelve graficando:
\(\left\{\begin{aligned} x+y=&−1\\−2x−2y&=2 \end{aligned}\right.\).
- Contestar
-
\((x,-x-1)\)
Claves para llevar
- En esta sección, limitamos nuestro estudio a sistemas de dos ecuaciones lineales con dos variables. Las soluciones a tales sistemas, si existen, consisten en pares ordenados que satisfacen ambas ecuaciones. Geométricamente, las soluciones son los puntos donde se cruzan las gráficas.
- El método de graficación para resolver sistemas lineales nos obliga a graficar ambas líneas en el mismo conjunto de ejes como medio para determinar dónde se cruzan.
- El método de graficación no es el método más preciso para determinar soluciones, particularmente cuando las soluciones tienen coordenadas que no son números enteros. Es una buena práctica comprobar siempre sus soluciones.
- Algunos sistemas lineales no tienen solución simultánea. Estos sistemas consisten en ecuaciones que representan líneas paralelas con diferentes\(y\) -intercepciones y no se cruzan en el plano. Se les llama sistemas inconsistentes y el conjunto de soluciones es el conjunto vacío,\(Ø\).
- Algunos sistemas lineales tienen infinitamente muchas soluciones simultáneas. Estos sistemas consisten en ecuaciones que son equivalentes y representan la misma línea. Se les llama sistemas dependientes y sus soluciones se expresan usando la notación\((x, mx+b)\), donde\(x\) está cualquier número real.
Ejercicio\(\PageIndex{4}\) Solutions to Linear Systems
Determinar si el par ordenado dado es una solución al sistema dado.
- \((3, −2); \left\{\begin{aligned} x+y&=-1\\-2x-2y&=2 \end{aligned}\right.\)
- \((−5, 0); \left\{\begin{aligned} x+y&=−1\\−2x−2y&=2 \end{aligned}\right.\)
- \((−2, −6); \left\{\begin{aligned}−x+y&=−4\\3x−y&=−12 \end{aligned}\right.\)
- \((2, −7); \left\{\begin{aligned} 3x+2y&=−8\\−5x−3y&=11 \end{aligned}\right.\)
- \((0, −3); \left\{\begin{aligned}5x−5y&=15\\−13x+2y&=−6 \end{aligned}\right.\)
- \((−12, 14); \left\{\begin{aligned} x+y&=−14\\−2x−4y&=0 \end{aligned}\right.\)
- \((\frac{3}{4}, \frac{1}{4}); \left\{\begin{aligned} −x−y&=−1\\−4x−8y&=5 \end{aligned}\right.\)
- \((−3, 4); \left\{\begin{aligned} \frac{1}{3}x+\frac{1}{2}y&=1 \\ \frac{2}{3}x−\frac{3}{2}y&=−8 \end{aligned}\right.\)
- \((−5, −3); \left\{\begin{aligned} y&=−35x−10 \\ y&=5 \end{aligned}\right.\)
- \((4, 2); \left\{\begin{aligned} x&=4−7\\x+4y&=8 \end{aligned}\right.\)
- Contestar
-
1. No
3. No
5. Sí
7. No
9. Sí
Ejercicio\(\PageIndex{5}\) Solutions to Linear Systems
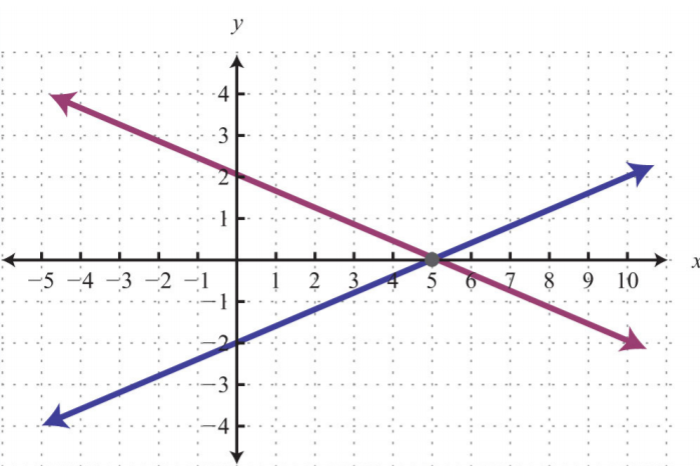
Dada la gráfica, determinar la solución simultánea.
1.
.png)
2.
.png)
3.
.png)
4.
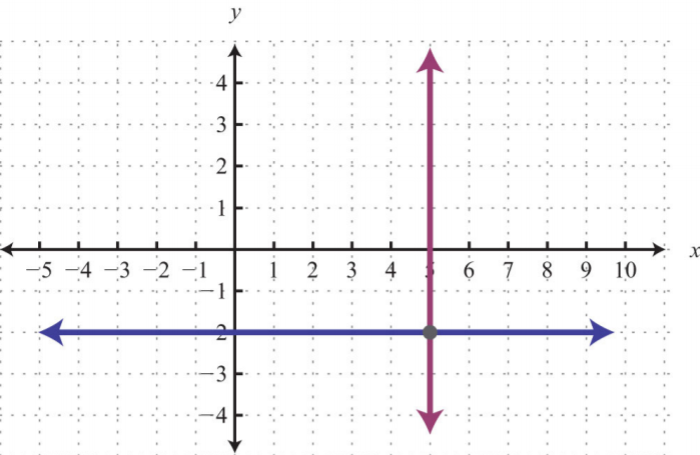.png)
5.
.png)
6.
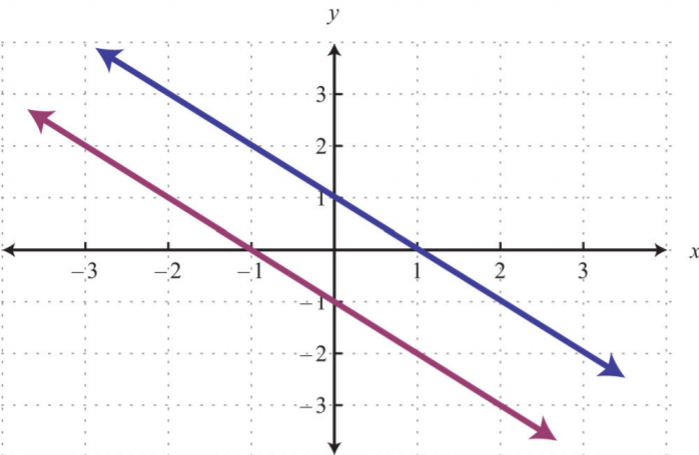.png)
7.
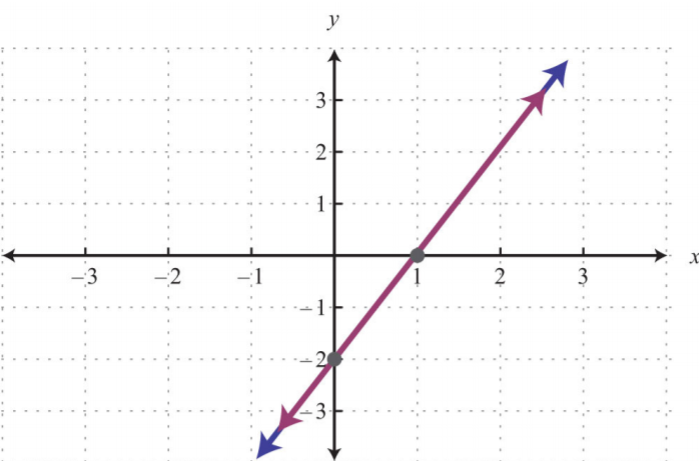.png)
8.
.png)
9.
.png)
10.
.png)
Figura\(\PageIndex{18}\)
- Contestar
-
1. \((5, 0)\)
3. \((2, 1)\)
5. \((0, 0)\)
7. \((x, 2x−2)\)
9. \(∅\)
Ejercicio\(\PageIndex{6}\) Solving Linear Systems
Resuelve graficando.
- \(\left\{\begin{aligned} y &=\frac{3}{2}x + 6\\y&=−x + 1 \end{aligned}\right.\)
- \(\left\{\begin{aligned} y& =\frac{3}{4}x + 2\\y&=−\frac{1}{4}x − 2 \end{aligned}\right.\)
- \(\left\{\begin{aligned} y& =x − 4\\y&=−x + 2 \end{aligned}\right.\)
- \(\left\{\begin{aligned} y&=− 5 x + 4\\y& = 4 x − 5 \end{aligned}\right.\)
- \(\left\{\begin{aligned} y& =\frac{2}{5} x + 1\\ y& =\frac{3}{5} x \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=−\frac{2}{5} x + 6\\y& =\frac{2}{5} x +10 \end{aligned}\right.\)
- \(\left\{\begin{aligned} y&=− 2\\y& =x + 1 \end{aligned}\right.\)
- \(\left\{\begin{aligned} y& = 3\\ x&=− 3 \end{aligned}\right.\)
- \(\left\{\begin{aligned} y& = 0\\y& =\frac{2}{5} x − 4 \end{aligned}\right.\)
- \(\left\{\begin{aligned} x& = 2 \\y& = 3 x \end{aligned}\right.\)
- \(\left\{\begin{aligned} y& =\frac{3}{5} x − 6\\y& =\frac{3}{5} x − 3 \end{aligned}\right.\)
- \(\left\{\begin{aligned} y&=−\frac{1}{2}x + 1\\ y&=−\frac{1}{2}x + 1 \end{aligned}\right.\)
- \(\left\{\begin{aligned}2 x + 3 y &=18 \\ − 6 x + 3 y&=− 6 \end{aligned}\right.\)
- \(\left\{\begin{aligned} − 3 x + 4y &=20\\2 x + 8y &= 8\end{aligned}\right.\)
- \(\left\{\begin{aligned} − 2 x +y &=1 \\2 x − 3 y& = 9\end{aligned}\right.\)
- \(\left\{\begin{aligned} x + 2y&=−8\\5 x + 4y&=− 4\end{aligned}\right.\)
- \(\left\{\begin{aligned}4 x + 6y &=36\\2 x − 3 y &= 6\end{aligned}\right.\)
- \(\left\{\begin{aligned} 2 x − 3 y &=18\\6 x − 3 y&=− 6\end{aligned}\right.\)
- \(\left\{\begin{aligned} 3 x + 5y &=30\\ − 6 x −10y&=−10\end{aligned}\right.\)
- \(\left\{\begin{aligned}−x + 3 y &=3\\5 x −15 y&=−15\end{aligned}\right.\)
- \(\left\{\begin{aligned}x −y &= 0\\ −x +y &= 0\end{aligned}\right.\)
- \(\left\{\begin{aligned}y &=x\\y −x& = 1\end{aligned}\right.\)
- \(\left\{\begin{aligned}3 x + 2y &= 0\\ x &= 2\end{aligned}\right.\)
- \(\left\{\begin{aligned}2 x +\frac{1}{3}y &=\frac{2}{3}\\ − 3 x +12y&=− 2\end{aligned}\right.\)
- \(\left\{\begin{aligned}\frac{1}{10}x +\frac{1}{5}y &= 2\\ −\frac{1}{5} x +\frac{1}{5}y&=− 1\end{aligned}\right.\)
- \(\left\{\begin{aligned}\frac{1}{3} x −\frac{1}{2}y &= 1 \\ \frac{1}{3} x +\frac{1}{5}y& = 1 \end{aligned}\right.\)
- \(\left\{\begin{aligned} \frac{1}{9}x +\frac{1}{6}y &= 0 \\ \frac{1}{9}x +\frac{1}{4}y &=\frac{1}{2}\end{aligned}\right.\)
- \(\left\{\begin{aligned} \frac{5}{16}x −\frac{1}{2}y &= 5\\ −\frac{5}{16}x +\frac{1}{2}y &=\frac{5}{2} \end{aligned}\right.\)
- \(\left\{\begin{aligned} \frac{1}{6}x−\frac{1}{2}y&=\frac{9}{2} \\ −\frac{1}{18}x+\frac{1}{6}y&=−\frac{3}{2} \end{aligned}\right.\)
- \(\left\{\begin{aligned} \frac{1}{2}x−\frac{1}{4}y&=−\frac{1}{2} \\ \frac{1}{3}x−\frac{1}{2}y&=3\end{aligned}\right.\)
- \(\left\{\begin{aligned} y&=4\\x&=−5 \end{aligned}\right.\)
- \(\left\{\begin{aligned} y&=−3\\x&=2\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=0\\x&=0\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=−2\\y&=3\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=5\\y&=−5\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=2\\y−2&=0\end{aligned}\right.\)
- \(\left\{\begin{aligned}x&=−5\\x&=1\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=x\\x&=0\end{aligned}\right.\)
- \(\left\{\begin{aligned}4x+6y&=3\\−x+y&=−2\end{aligned}\right.\)
- \(\left\{\begin{aligned}−2x+20y&=20\\3x+10y&=−10\end{aligned}\right.\)
- Contestar
-
1. \((−2, 3)\)
3. \((3, −1)\)
5. \((5, 3)\)
7. \((−3, −2)\)
9. \((10, 0)\)
11. \(∅\)
13. \((3, 4)\)
15. \((−3, −5)\)
17. \((6, 2)\)
19. \(∅\)
21. \((x, x)\)
23. \((2, −3)\)
25. \((10, 5)\)
27. \((−9, 6)\)
29. \((x, 13x−9)\)
31. \((−5, 4)\)
33. \((0, 0)\)
35. \(∅\)
37. \(∅\)
39. \((\frac{3}{2}, −\frac{1}{2})\)
Ejercicio\(\PageIndex{7}\) Solving Linear Systems
Establecer un sistema lineal de dos ecuaciones y dos variables y resolverlo usando el método de graficación.
- La suma de dos números es
- El número mayor es\(10\) menos de cinco veces el menor.
- La diferencia entre dos números es\(12\) y su suma es\(4\).
- ¿Dónde en la gráfica de la\(3x−2y=6\)\(x\) coordenada -iguala la\(y\) coordenada -coordenada?
- ¿Dónde en la gráfica de la\(−5x+2y=30\)\(x\) coordenada -iguala la\(y\) coordenada -coordenada?
- Contestar
-
1. Los dos números son\(5\) y\(15\).
3. \((6, 6)\)
Ejercicio\(\PageIndex{8}\) Solving Linear Systems
Una empresa regional de agua embotellada produce y vende agua embotellada. La siguiente gráfica representa las curvas de oferta y demanda de agua embotellada en la región. El eje horizontal representa el tonelaje semanal del producto producido,\(Q\). El eje vertical representa el precio por botella en dólares,\(P\).
.png)
Figura\(\PageIndex{19}\)
Utilice la gráfica para responder a las siguientes preguntas.
- Determinar el precio al que la cantidad demandada es igual a la cantidad suministrada.
- Si la producción de agua embotellada se desliza a\(20\) toneladas, entonces ¿qué precio predice la curva de demanda para una botella de agua?
- Si la producción de agua embotellada aumenta a\(40\) toneladas, entonces ¿qué precio predice la curva de demanda para una botella de agua?
- Si el precio del agua embotellada se fija en $\(2.50\) dólares por botella, ¿qué cantidad predice la curva de demanda?
- Contestar
-
1. $\(1.25\)
3. $\(1.00\)
Ejercicio\(\PageIndex{9}\) Discussion Board Topics
- Discutir las debilidades del método de graficación para resolver sistemas.
- Explicar por qué la solución establecida en un sistema lineal dependiente se denota por\((x, mx+ b)\).
- Contestar
-
1. Las respuestas pueden variar


