4.2: Resolver sistemas lineales por sustitución
( \newcommand{\kernel}{\mathrm{null}\,}\)
Objetivos de aprendizaje
- Resolver sistemas lineales utilizando el método de sustitución.
El método de sustitución
En esta sección, definiremos una técnica completamente algebraica para resolver sistemas. La idea es resolver una ecuación para una de las variables y sustituir el resultado por la otra ecuación. Después de realizar este paso de sustitución, nos quedaremos con una sola ecuación con una variable, la cual puede resolverse usando álgebra. Esto se denomina método de sustitución, y los pasos se describen en el siguiente ejemplo.
Ejemplo4.2.1
Resolver por sustitución:
Solución:
Paso 1: Resuelve para cualquiera de las variables en cualquiera de las ecuaciones. Si eliges la primera ecuación, puedes aislartey en un solo paso.
2x+y=72x+y−2x=7−2xy=−2x+7
Paso 2: Sustituir la expresión−2x+7 por lay variable en la otra ecuación.
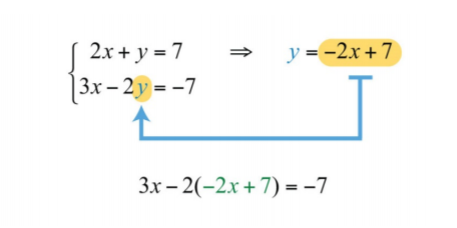.png)
Esto te deja con una ecuación equivalente con una variable, que se puede resolver utilizando las técnicas aprendidas hasta este punto.
Paso 3: Resolver para la variable restante. Para resolverx, primero distribuya−2:
Paso 4: Volver sustituto para encontrar el valor de la otra coordenada. Sustituirx=1 en cualquiera de las ecuaciones originales o sus equivalentes. Normalmente, usamos la ecuación equivalente que encontramos al aislar una variable en el paso 1.
y=−2x+7=−2(1)+7=−2+7=5
La solución al sistema es(1,5). Asegúrese de presentar la solución como un par ordenado.
Paso 5: Comprobar. Verifique que estas coordenadas resuelvan ambas ecuaciones del sistema original:
Check:(1,5)
Equation1:Equation2:2x+y=73x−2y=−72(1)+(5)=73(1)−2(5)=−72+5=73−10=−77=7✓−7=−7✓
La gráfica de este sistema lineal sigue:
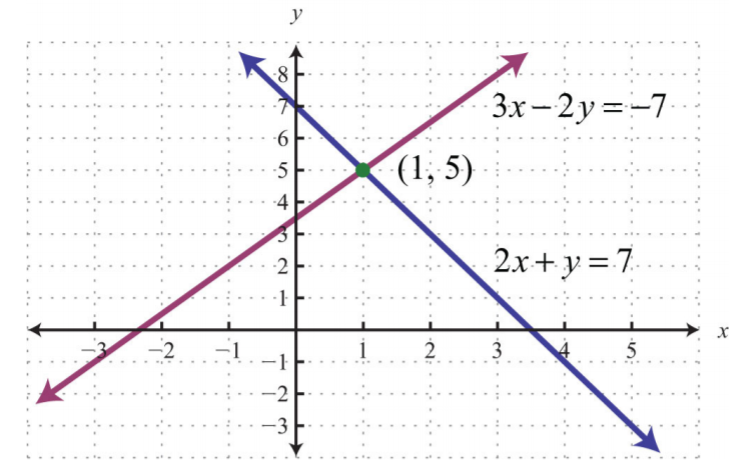.png)
El método de sustitución para resolver sistemas es un método completamente algebraico. Por lo tanto, no se requiere graficar las líneas.
Respuesta:
(1,5)
Ejemplo4.2.2
Resolver por sustitución:
{2x−y=12x−y=3.
Solución:
En este ejemplo, podemos ver quex tiene un coeficiente de1 en la segunda ecuación. Esto indica que se puede aislar en un solo paso de la siguiente manera:
x−y=3x−y+y=3+yx=3+y
{2x−y=12x−y=3⇒x=3+y
Sustituto3+yx en la primera ecuación. Use paréntesis y tenga cuidado de distribuir.
2x−y=122(3+y)−y=126+2y−y=126+y=126+y−6=12−6y=6
x=3+yÚselo para encontrarx.
x=3+y=3++6=9
Respuesta:
(9,6). El cheque se deja al lector.
Ejemplo4.2.3
Resolver por sustitución:
{3x−5y=17x=−1.
Solución:
En este ejemplo, la variable yax está aislada. De ahí que podamos sustituirx=−1 en la primera ecuación.
Respuesta:
(−1,−4). Es un buen ejercicio graficar este sistema en particular para comparar el método de sustitución con el método de graficación para resolver sistemas.
Ejercicio4.2.1
Resolver por sustitución:
{3x+y=48x+2y=10.
- Contestar
-
(1,1)
Resolver sistemas algebraicamente con frecuencia requiere trabajar con fracciones.
Ejemplo4.2.4
Resolver por sustitución:
{2x+8y=524x−4y=−15.
Solución:
Comienza por resolver parax en la primera ecuación.
2x+8y=52x+8y−8y=5−8y2x2=−8y+52x=−8y2+52x=−4y+52
{2x+8y=5⇒x=−4y+5224x−4y=−15
A continuación, sustituya en la segunda ecuación y resuelva paray.
Volver a sustituir en la ecuación utilizada en el paso de sustitución:
x=−4y+52=−4(34)+52=−3+52=−62+52=−12
Respuesta:
(−12,34)
Como sabemos, no todos los sistemas lineales tienen solo una solución de par ordenado. Recordemos que algunos sistemas tienen infinitamente muchas soluciones de pares ordenados y algunos no tienen ninguna solución. A continuación, exploramos lo que sucede cuando se utiliza el método de sustitución para resolver un sistema dependiente.
Ejemplo4.2.5
Resolver por sustitución:
{−5x+y=−110x−2y=2.
Solución:
Dado que la primera ecuación tiene un término con coeficiente1, elegimos resolver para eso primero.
A continuación, sustituya esta expresión pory en la segunda ecuación.
10x−2y=210x−2(5x−1)=210x−10x+2=22=2True
Este proceso condujo a una afirmación verdadera; de ahí que la ecuación sea una identidad y cualquier número real es una solución. Esto indica que el sistema es dependiente. Las soluciones simultáneas toman la forma(x,mx+b), o en este caso,(x,5x−1), dondex está cualquier número real.
Respuesta:
(x,5x−1)
Para tener una mejor comprensión del ejemplo anterior, reescribe ambas ecuaciones en forma de pendiente-intercepción y graficarlas en el mismo conjunto de ejes.
Podemos ver que ambas ecuaciones representan la misma línea, y así el sistema es dependiente. Ahora explora lo que sucede al resolver un sistema inconsistente usando el método de sustitución.
Ejemplo4.2.6
Resolver por sustitución:
{−7x+3y=314x−6y=−16.
Solución:
Resuelve paray en la primera ecuación.
−7x+3y=3−7x+3y+7x=3+7x3y=7x+33y3=7x+33y=73x+1
{−7x+3y=3⇒y=73x+114x−6y=−16
Sustituir en la segunda ecuación y resolver.
Resolver conduce a una declaración falsa. Esto indica que la ecuación es una contradicción. No hay solución parax y por lo tanto no hay solución para el sistema.
Respuesta:
Sin solución,Ø
Una declaración falsa indica que el sistema es inconsistente, o en términos geométricos, que las líneas son paralelas y no se cruzan. Para ilustrar esto, determine la forma pendiente-intercepción de cada línea y gráfiquelas en el mismo conjunto de ejes.
En forma de pendiente-intercepción, es fácil ver que las dos líneas tienen la misma pendiente pero diferentesy -intercepciones.
Ejercicio4.2.2
Resolver por sustitución:
{2x−5y=34x−10y=6.
- Contestar
-
(x,25x−35)
Claves para llevar
- El método de sustitución es un método completamente algebraico para resolver un sistema de ecuaciones.
- El método de sustitución requiere que resolvamos una de las variables y luego sustituimos el resultado por la otra ecuación. Después de realizar la etapa de sustitución, la ecuación resultante tiene una variable y se puede resolver utilizando las técnicas aprendidas hasta este punto.
- Cuando se determine el valor de una de las variables, retroceda y sustituya por una de las ecuaciones originales, o sus ecuaciones equivalentes, para determinar el valor correspondiente de la otra variable.
- Las soluciones a sistemas de dos ecuaciones lineales con dos variables, si existen, son pares ordenados(x,y).
- Si el proceso de resolver un sistema de ecuaciones conduce a una declaración falsa, entonces el sistema es inconsistente y no hay solución,Ø.
- Si el proceso de resolver un sistema de ecuaciones conduce a una afirmación verdadera, entonces el sistema es dependiente y hay infinitamente muchas soluciones que se pueden expresar usando la forma(x,mx+b).
Ejercicio4.2.3 Substitution Method
Resolver por sustitución.
- {y=4x−1−3x+y=1
- {y=3x−84x−y=2
- {x=2y−3x+3y=−8
- {x=−4y+12x+3y=12
- {y=3x−5x+2y=2
- {y=x2x+3y=10
- {y=4x+1−4x+y=2
- {y=−3x+53x+y=5
- {y=2x+32x−y=−3
- {y=5x−1x−2y=5
- {y=−7x+13x−y=4
- {x=6y+25x−2y=0
- {y=−2−2x−y=−6
- {x=−3x−4y=−3
- {y=−15x+37x−5y=9
- {y=23x−16x−9y=0
- {y=12x+13x−6y=4
- {y=−38x+122x+4y=1
- {x+y=62x+3y=16
- {x−y=3−2x+3y=−2
- {2x+y=23x−2y=17
- {x−3y=−113x+5y=−5
- {x+2y=−33x−4y=−2
- {5x−y=129x−y=10
- {x+2y=−6−4x−8y=24
- {x+3y=−6−2x−6y=−12
- {−3x+y=−46x−2y=−2
- {x−5y=−102x−10y=−20
- {3x−y=94x+3y=−1
- {2x−y=54x+2y=−2
- {−x+4y=02x−5y=−6
- {3y−x=55x+2y=−8
- {2x−5y=14x+10y=2
- {3x−7y=−36x+14y=0
- {10x−y=3−5x+12y=1
- {−13x+16y=2312x−13y=−32
- {13x+23y=114x−13y=−112
- {17x−y=1214x+12y=2
- {−35x+25y=1213x−112y=−13
- {12x=23yx−23y=2
- {−12x+12y=5814x+12y=14
- {x−y=0−x+2y=3
- {y=3x2x−3y=0
- {2x+3y=18−6x+3y=−6
- {−3x+4y=202x+8y=8
- {5x−3y=−13x+2y=7
- {−3x+7y=22x+7y=1
- {y=3y=−3
- {x=5x=−2
- {y=4y=4
- Contestar
-
1. (2,7)
3. (−5,−1)
5. (2,6)
7. ∅
9. (x,2x+3)
11. (12,−52)
13. (4,−2)
15. (3,125)
17. (−3,−76)
19. (2,4)
21. (3,−4)
23. (−85,−710)
25. (x,−12x−3)
27. ∅
29. (2,−3)
31. (−8,−2)
33. (12,0)
35. ∅
37. (1,1)
39. (−1110,−25)
41. (−12,34)
43. (0,0)
45. (−4,2)
47. (−15,15)
49. ∅
Ejercicio4.2.4 Substitution Method
Configurar un sistema lineal y resolverlo usando el método de sustitución.
- La suma de dos números es19. El número mayor es1 menos de tres veces el menor.
- La suma de dos números es15. Cuanto más grande es3 más del doble de menor.
- La diferencia de dos números es7 y su suma es1.
- La diferencia de dos números es3 y su suma es−7.
- ¿Dónde en la gráfica de la−5x+3y=30x coordenada -iguala lay coordenada -coordenada?
- ¿Dónde en la gráfica de la12x−13y=1x coordenada -iguala lay coordenada -coordenada?
- Contestar
-
1. Los dos números son5 y14.
3. Los dos números son4 y−3.
5. (−15,−15)
Ejercicio4.2.5 Discussion Board Topics
- Describir qué impulsa la elección de la variable a resolver al iniciar el proceso de resolución por sustitución.
- Discutir los méritos e inconvenientes del método de sustitución.
- Contestar
-
1. Las respuestas pueden variar


