4.4: Aplicaciones de Sistemas Lineales

Última actualización
Guardar como PDF

Page ID: 110151

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Configure y resuelva aplicaciones que involucren relaciones entre números.
Configurar y resolver aplicaciones que involucren intereses y dinero.
Configurar y resolver problemas de mezcla.
Configure y resuelva problemas de movimiento uniforme (problemas de distancia).

Problemas que involucran relaciones entre números reales

Ahora contamos con las técnicas necesarias para resolver sistemas lineales. Por esta razón, ya no nos limitamos a usar una variable al configurar ecuaciones que modelan aplicaciones. Si traducimos una aplicación a una configuración matemática usando dos variables, entonces necesitamos formar un sistema lineal con dos ecuaciones.

Ejemplo$\PageIndex{1}$

La suma de dos números es$40$ y su diferencia es$8$. Encuentra los números.

Solución:

Identificar variables:

Vamos a$x$ representar uno de los números desconocidos.

Vamos a$y$ representar el otro número desconocido.

Configurar ecuaciones:

Al usar dos variables, necesitamos establecer dos ecuaciones. La primera frase clave, “la suma de los dos números es”$40$, se traduce de la siguiente manera:

$x+y=40$

Y la segunda frase clave, “la diferencia es”$8$, nos lleva a la segunda ecuación:

$x-y=8$

Por lo tanto, nuestra configuración algebraica consiste en el siguiente sistema:

$\left\{\begin{aligned} x+y&=40 \\ x-y&=8 \end{aligned}\right.$

Resolver :

Podemos resolver el sistema resultante utilizando cualquier método de nuestra elección. Aquí elegimos resolver por eliminación. Al sumar las ecuaciones se elimina la variable$y$.

$\begin{aligned} x\color{red}{+y}&=40 \\ \underline{+\quad x\color{red}{-y}}&\underline{=8} \\ 2x&=48 \\ x&=24 \end{aligned}$

Una vez que tenemos$x$, volver sustituto para encontrar$y$.

$\begin{aligned} x+y&=40 \\ \color{OliveGreen}{24}\color{black}{+y}&=40 \\ 24+y\color{Cerulean}{-24}&=40\color{Cerulean}{-24} \\ y&=16 \end{aligned}$

Comprobar:

La suma de los dos números debe ser$42$ y su diferencia$8$.

$\begin{aligned} 24+16&=40 \\ 24-16&=8 \end{aligned}$

Respuesta:

Los dos números son$24$ y$16$.

Ejemplo$\PageIndex{2}$

La suma de$9$ veces un número mayor y dos veces menor es$6$. La diferencia de$3$ veces cuanto mayor y menor es$7$. Encuentra los números.

Solución:

Comience asignando variables al número mayor y menor.

Let$x$ representar el número mayor.

Let$y$ representar el número más pequeño.

La primera frase describe una suma y la segunda frase describe una diferencia.

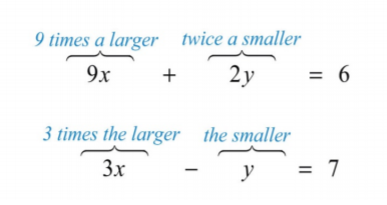Captura de pantalla (416) .png — Figura$\PageIndex{1}$

Esto lleva al siguiente sistema:

$\left\{\begin{aligned} 9x+2y&=6\\3x-y&=7 \end{aligned}\right.$

Resuelve usando el método de eliminación. Multiplica la segunda ecuación por$2$ y suma.

$\left\{\begin{aligned} 9x+2y&=6 \\ 3x-y&=7 \end{aligned}\right. \stackrel{\times 2}{\Rightarrow} \left\{\begin{aligned} 9x+2y&=6\\ 6x-2y&=14 \end{aligned}\right.$

$\begin{aligned} 9x\color{red}{+2y}&=6\\ \underline{+\quad 6x\color{red}{-2y}}&\underline{=14} \\ 15x&=20 \\ x&=\frac{20}{15} \\ x&=\frac{4}{3} \end{aligned}$

Volver sustituto para encontrar$y$.

Respuesta:

El número mayor es$\frac{4}{3}$ y el número menor es$−3$.

Ejercicio$\PageIndex{1}$

La suma de dos números es$3$. Cuando se resta el doble del número menor de$6$ veces mayor es el resultado$22$. Encuentra los números.

Contestar: Los dos números son$−\frac{1}{2}$ y$\frac{7}{2}$.

Problemas de interés y dinero

En esta sección, los problemas de interés y dinero deberían parecer familiares. La diferencia es que vamos a estar haciendo uso de dos variables a la hora de configurar las ecuaciones algebraicas.

Ejemplo$\PageIndex{3}$

Un rollo de$32$ billetes contiene solo $$5$ facturas y $$10$ facturas. Si el valor del rollo es $$220$, entonces ¿cuántos de cada billete hay en el rollo?

Solución:

Comience por identificar las variables.

Dejar$x$ representar el número de$5$ billetes de $.

Dejar$y$ representar el número de$10$ billetes de $.

Al usar dos variables, necesitamos establecer dos ecuaciones. La primera ecuación se crea a partir del hecho de que hay$32$ facturas.

$x+y=32$

La segunda ecuación suma el valor de cada billete: el valor total es $$220$.

$5\cdot x+$$$10\cdot y=$ $$220$

Presentar ambas ecuaciones como un sistema; esta es nuestra configuración algebraica.

$\left\{\begin{aligned} x+y&=32 \\ 5x+10y&=220 \end{aligned}\right.$

Aquí elegimos resolver por eliminación, aunque la sustitución funcionaría igual de bien. Eliminar$x$ multiplicando la primera ecuación por$−5$.

Ahora suma las ecuaciones juntas:

Una vez que tenemos$y$, el número de$10$ billetes de $, volver a sustituir para encontrar$x$.

$\begin{aligned} x+y&=32 \\ x+\color{OliveGreen}{12}&=32 \\ x+12\color{Cerulean}{-12}&=32\color{Cerulean}{-12} \\ x&=20 \end{aligned}$

Respuesta:

Hay$5$ billetes de veinte $ y doce$10$ billetes de $. El cheque se deja al lector.

Ejemplo$\PageIndex{4}$

Se$6,300$ invirtió un total de $ en dos cuentas. Parte se invirtió en un CD a una tasa de interés anual$4\frac{1}{2}$% y parte se invirtió en un fondo del mercado monetario a una tasa de interés$3\frac{3}{4}$% anual. Si el interés simple total por un año fue $$267.75$, entonces ¿cuánto se invirtió en cada cuenta?

Solución:

Dejar$x$ representar la cantidad invertida en$4\frac{1}{2}$%$=4.5$%$=0.045$

Dejar$y$ representar la cantidad invertida en$3\frac{3}{4}$%$=3.75$%$=0.0375$

El monto total en ambas cuentas se puede expresar como

$x+y=6,300$

Para establecer una segunda ecuación, utilice el hecho de que el interés total fue $$267.75$. Recordemos que el interés por un año es la tasa de interés multiplicada por el principal$(I=prt=pr⋅1=pr)$. Utilízalo para sumar los intereses en ambas cuentas. Asegúrese de usar los equivalentes decimales para las tasas de interés dadas como porcentajes.

$\begin{array}{ccccc}{\color{Cerulean}{interest\:from\:the\:CD}}&{\color{Cerulean}{+}}&{\color{Cerulean}{interest\:from\:the\:fund}}&{\color{Cerulean}{=}}&{\color{Cerulean}{total\:interest}}\\{0.045x}&{+}&{0.375y}&{=}&{267.75} \end{array}$

Estas dos ecuaciones juntas forman el siguiente sistema lineal:

$\left\{\begin{aligned} x+y&=6,300 \\ 0.045x+0.0375y&=267.75 \end{aligned}\right.$

Eliminar$y$ multiplicando la primera ecuación por$−0.0375$.

$\left\{\begin{aligned} x+y&=6,300 \\ 0.045x+0.0375y&=267.75 \end{aligned}\right. \stackrel{\times (-0.0375)}{\Rightarrow} \left\{\begin{aligned} -0.0375x-0.0375y&=-236.25 \\ 0.045x+0.0375y&=267.75 \end{aligned}\right.$

A continuación, sumar las ecuaciones juntas para eliminar la variable$y$.

$\begin{aligned} -0.0375x\color{red}{-0.0375y}&=-236.25 \\ \underline{+\quad 0.045x\color{red}{+0.0375y}}&\underline{=267.75} \\ 0.0075x&=31.5 \\ \frac{0.0075x}{\color{Cerulean}{0.0075}}&=\frac{31.5}{\color{Cerulean}{0.0075}} \\ x&=4,200 \end{aligned}$

Sustituto de espalda.

$\begin{aligned} x+y&=6,300 \\ \color{OliveGreen}{4,200}\color{black}{+y}&=6,300 \\ 4,200+y\color{Cerulean}{-4,200}&=6,300\color{Cerulean}{-4,200} \\ y&=2,100 \end{aligned}$

Respuesta:

$$4,200$ se invirtió en$4\frac{1}{2}$% y $$2,100$ se invirtió en$3\frac{3}{4}$%

En este punto, deberíamos poder resolver este tipo de problemas de dos maneras: con una variable y ahora con dos variables. Establecer problemas verbales con dos variables a menudo simplifica todo el proceso, particularmente cuando las relaciones entre las variables no son tan claras.

Ejercicio$\PageIndex{2}$

El primer día de una reunión de dos días, se compraron$10$ cafés y$10$ donas por un total de $$20.00$. Ya que nadie bebió el café y se comieron todas las donas, al día siguiente solo se compraron$2$ cafés y$14$ donas por un total de $$13.00$. ¿Cuánto costó cada café y cada rosquilla?

Contestar: Café: $$1.25$; donas: $$0.75$

Problemas de mezcla

Los problemas de mezcla suelen incluir un porcentaje y alguna cantidad total. Es importante hacer una distinción entre estos dos tipos de cantidades. Por ejemplo, si un problema indica que un recipiente de$20$ -onza se llena con una solución salina (sal)$2$%, entonces esto significa que el recipiente se llena con una mezcla de sal y agua de la siguiente manera:

Mesa$\PageIndex{1}$
	Porcentaje	Monto
Sal	$2$%$=0.02$	$0.02(20$onzas)$=0.4$ onzas
Agua	$98$%$=0.98$	$0.98(20$onzas)$=19.6$ onzas

Es decir, multiplicamos el porcentaje por el total para obtener la cantidad de cada parte de la mezcla.

Ejemplo$\PageIndex{5}$

Se combinará una solución salina en$2$% y se mezclará con una solución salina$5$% para producir$72$ onzas de una solución salina$2.5$%. ¿Cuánto de cada uno se necesita?

Solución:

Dejar$x$ representar la cantidad de$2$% de solución salina necesaria.

Dejar$y$ representar la cantidad de$5$% de solución salina necesaria.

La cantidad total de solución salina necesaria es de$72$ onzas. Esto lleva a una ecuación,

$x+y=72$

La segunda ecuación suma la cantidad de sal en los porcentajes correctos. La cantidad de sal se obtiene multiplicando el porcentaje por la cantidad, donde las variables$x$ y$y$ representan las cantidades de las soluciones.

$\begin{array}{ccccc}{\color{Cerulean}{salt\:in2\%\:solution}}&{\color{Cerulean}{+}}&{\color{Cerulean}{salt\:in\:5\%\:solution}}&{\color{Cerulean}{=}}&{\color{Cerulean}{salt\:in\:the\:end\:solution}}\\{0.02x}&{+}&{0.05y}&{=}&{0.025(72)}\end{array}$

Resolver.

$\left\{\begin{aligned} x+y&=72 \\ 0.02x+0.05y&=0.025(72) \end{aligned}\right. \stackrel{\times (-0.02)}{\Rightarrow} \left\{\begin{aligned} -0.02x-0.02y&=-1.44 \\ 0.02x+0.05y&=1.8 \end{aligned}\right.$

$\begin{aligned} \color{red}{-0.02x}\color{black}{-0.02y}&=-1.44 \\ \underline{+\quad\color{red}{0.02x}\color{black}{+0.05y}}&\underline{=1.8} \\ 0.03y&=0.36 \\ \frac{0.03y}{\color{Cerulean}{0.03}}&=\frac{0.36}{\color{Cerulean}{0.03}} \\ y&=12 \end{aligned}$

Sustituto de espalda.

$\begin{aligned} x+y&=72 \\ x+\color{OliveGreen}{12}&=72 \\ x+12\color{Cerulean}{-12}&=72\color{Cerulean}{-12} \\ x&=60 \end{aligned}$

Respuesta:

Necesitamos$60$ onzas del$2$% de solución salina y$12$ onzas de la solución salina$5$%.

Ejemplo$\PageIndex{6}$

Una solución de$50$% de alcohol se va a mezclar con una solución de$10$% de alcohol para crear una mezcla de$8$ -onza de una solución de$32$% de alcohol. ¿Cuánto de cada uno se necesita?

Solución:

Dejar$x$ representar la cantidad de$50$% de solución de alcohol necesaria.

Dejar$y$ representar la cantidad de$10$% de solución de alcohol necesaria.

La cantidad total de la mezcla debe ser de$8$ onzas.

$x+y=8$

La segunda ecuación suma la cantidad de alcohol de cada solución en los porcentajes correctos. La cantidad de alcohol en el resultado final es$32$% de$8$ onzas, o$0.032(8)$.

$\begin{array}{ccccc}{\color{Cerulean}{alcohol\:in\:50\%\:solution}}&{\color{Cerulean}{+}}&{\color{Cerulean}{alcohol\:in\:10\%\:solution}}&{\color{Cerulean}{=}}&{\color{Cerulean}{alcohol\:in\:the\:end\:solution}}\\{0.50x}&{+}&{0.10y}&{=}&{0.32(8)}\end{array}$

Ahora podemos formar un sistema de dos ecuaciones lineales y dos variables de la siguiente manera:

$\left\{\begin{aligned} x+y&=8 \\ 0.50x+0.10y&=0.32(8) \end{aligned}\right.$

En este ejemplo, multiplica la segunda ecuación por$100$ para eliminar los decimales. Además, multiplique la primera ecuación por$−10$ para alinear la variable$y$ a eliminar.

$\begin{array}{c|c} {Equation\:1:}&{Equation\:2:}\\{\color{Cerulean}{-10}\color{black}{(x+y)=}\color{Cerulean}{-10}\color{black}{(8)}}&{\color{Cerulean}{100}\:\color{black}{0.50x+0.10y=}\color{Cerulean}{100}\color{black}{(0.32)(8)}}\\{-10x-10y=-80}&{50x+10y=256} \end{array}$

Obtenemos el siguiente sistema equivalente:

Agregue las ecuaciones y luego resuelva para$x$:

Sustituto de espalda.

$\begin{aligned} x+y&=8 \\ \color{OliveGreen}{4.4}\color{black}{+y}&=8 \\ 4.4+y\color{Cerulean}{-4.4}&=8\color{Cerulean}{-4.4} \\ x&=3.6 \end{aligned}$

Respuesta:

Para obtener$8$ onzas de una mezcla de$32$% de alcohol necesitamos mezclar$4.4$ onzas de la solución$50$% de alcohol y$3.6$ onzas de la solución$10$%.

Ejercicio$\PageIndex{3}$

Un concentrado de$70$% anticongelante se va a mezclar con agua para producir una mezcla de$5$ -galón que contiene$28$% de anticongelante. ¿Cuánta agua y concentrado anticongelante se necesita?

Contestar: Necesitamos mezclar$3$ galones de agua con$2$ galones de concentrado anticongelante.

Problemas de movimiento uniforme (problemas de distancia)

Recordemos que la distancia recorrida es igual a la tasa promedio multiplicada por el tiempo recorrido a ese ritmo,$D=r⋅t$.

Estos problemas de movimiento uniforme suelen tener muchos datos, por lo que ayuda a organizar primero esos datos en un gráfico y luego configurar un sistema lineal. En esta sección, se le anima a utilizar dos variables.

Ejemplo$\PageIndex{7}$

Un ejecutivo viajó un total de$8$ horas y$1,930$ millas en automóvil y en avión. Conduciendo al aeropuerto en automóvil, promedió$60$ millas por hora. En el aire, el avión promedió$350$ millas por hora. ¿Cuánto tiempo le tomó conducir hasta el aeropuerto?

Solución:

Se nos pide encontrar el tiempo que le lleva conducir hasta el aeropuerto; esto indica que el tiempo es la cantidad desconocida.

Vamos a$x$ representar el tiempo que tardó en conducir hasta el aeropuerto.

Dejar$y$ representar el tiempo que se pasa en el aire.

Captura de pantalla (417) .png — Figura$\PageIndex{2}$

Usa la fórmula$D=r⋅t$ para rellenar las distancias desconocidas.

$\color{Cerulean}{Distance\:traveled\:in\:the\:car:}\quad\color{black}{D=r\cdot t=60\cdot x}$

$\color{Cerulean}{Distance\:traveled\:in\:the\:air:}\quad\color{black}{D=r\cdot t=350\cdot y}$

Captura de pantalla (418) .png — Figura$\PageIndex{3}$

La columna de distancia y la columna de tiempo del gráfico nos ayudan a configurar el siguiente sistema lineal.

Captura de pantalla (419) .png — Figura$\PageIndex{4}$

$\left\{\begin{aligned} x+y&=8 &\color{Cerulean}{\leftarrow\:total\:time\:traveled} \\ 6-x+350y&=1,930 &\color{Cerulean}{\leftarrow\:total\:distance\:traveled} \end{aligned}\right.$

Resolver.

Ahora vuelve sustituto para encontrar el tiempo que tardó en conducir hasta el aeropuerto$x$:

$\begin{aligned} x+y&=8 \\ x+\color{OliveGreen}{5}&=8 \\ x&=3 \end{aligned}$

Respuesta:

Le tomó$3$ horas conducir hasta el aeropuerto.

No siempre se da el caso de que el tiempo sea la cantidad desconocida. Lee el problema detenidamente e identifica lo que te piden que encuentres; esto define tus variables.

Ejemplo$\PageIndex{8}$

Volando con el viento, un avión viajó$1,365$ millas en$3$ horas. El avión giró entonces contra el viento y recorrió otras$870$ millas en$2$ horas. Encuentra la velocidad del avión y la velocidad del viento.

Solución:

No existe una relación obvia entre la velocidad del avión y la velocidad del viento. Por esta razón, utilice dos variables de la siguiente manera:

Dejar$x$ representar la velocidad del avión.

Dejar$w$ representar la velocidad del viento.

Utilice la siguiente tabla para organizar los datos:

Captura (420) .png — Figura$\PageIndex{5}$

Con el viento, la velocidad total del avión es$x+w$. Volando contra el viento, la velocidad total es$x−w$.

Captura de pantalla (421) .png — Figura$\PageIndex{6}$

Utilice las filas del gráfico junto con la fórmula$D=r⋅t$ para construir un sistema lineal que modele este problema. Tenga cuidado de agrupar entre paréntesis las cantidades que representan la tasa.

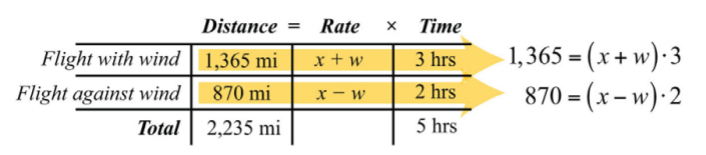Captura de pantalla (422) .png — Figura$\PageIndex{7}$

$\left\{\begin{aligned} 1,365&=(x+w)\cdot 3 &\color{Cerulean}{\leftarrow\:distance\:traveled\:with\:the\:wind} \\ 870&=(x-w)\cdot 2 &\color{Cerulean}{\leftarrow\:distance\:traveled\:against\:the\:wind} \end{aligned}\right.$

Si dividimos ambos lados de la primera ecuación por$3$ y ambos lados de la segunda ecuación por$2$, entonces obtenemos el siguiente sistema equivalente:

$\left\{\begin{aligned} 1,365&=(x+w)\cdot 3 \\ 870&=(x-w)\cdot 2 \end{aligned}\right. \begin{aligned} &\stackrel{\div 3}{\Rightarrow} \\ &\stackrel{\div 2}{\Rightarrow} \end{aligned} \left\{\begin{aligned} 455&=x+w \\ 435&=x-w \end{aligned}\right.$

$\begin{aligned} x\color{red}{+w}&=455 \\ \underline{+\quad x\color{red}{-w}}&\underline{=435} \\ 2x&=890 \\ \frac{2x}{\color{Cerulean}{2}}&=\frac{890}{\color{Cerulean}{2}} \\ x&=455 \end{aligned}$

Sustituto de espalda.

$\begin{aligned} x+w&=455 \\ \color{OliveGreen}{455}\color{black}{+w}&=455 \\ w&=10 \end{aligned}$

Respuesta:

La velocidad del avión es de$445$ millas por hora y la velocidad del viento es de$10$ millas por hora.

Ejercicio$\PageIndex{4}$

Un barco viajó$24$ millas río abajo en$2$ horas. El viaje de regreso, que estaba en contra de la corriente, tardó el doble de tiempo. ¿Cuáles son las velocidades de la embarcación y de la corriente?

Contestar: La velocidad de la embarcación es de$9$ millas por hora y la velocidad de la corriente es de$3$ millas por hora.

Claves para llevar

Utilice dos variables como medio para simplificar la configuración algebraica de aplicaciones donde la relación entre incógnitas no está clara.
Lee atentamente el problema varias veces. Si se utilizan dos variables, entonces recuerde que necesita configurar dos ecuaciones lineales para resolver el problema.
Asegúrese de responder la pregunta en forma de oración e incluya las unidades correctas para la respuesta.

Ejercicio$\PageIndex{5}$ Applications Involving Numbers

Configura un sistema lineal y resuelve.

La suma de dos enteros es$54$ y su diferencia es$10$. Encuentra los enteros.
La suma de dos enteros es$50$ y su diferencia es$24$. Encuentra los enteros.
La suma de dos enteros positivos es$32$. Cuando el entero más pequeño se resta del doble del mayor, el resultado es$40$. Encuentra los dos enteros.
La suma de dos enteros positivos es$48$. Cuando se resta el doble del entero más pequeño del mayor, el resultado es$12$. Encuentra los dos enteros.
La suma de dos enteros es$74$. Cuanto más grande es$26$ más del doble de menor. Encuentra los dos enteros.
La suma de dos enteros es$45$. Cuanto más grande es$3$ menos de tres veces más pequeño. Encuentra los dos enteros.
La suma de dos números es cero. Cuando las$4$ veces el número menor se agrega a$8$ veces el mayor, el resultado es$1$. Encuentra los dos números.
La suma de un número mayor y$4$ veces un número menor es$5$. Cuando los$8$ tiempos más pequeños se restan del doble de los mayores, el resultado es$−2$. Encuentra los números.
La suma de$12$ veces mayor número y$11$ veces menor es$−36$. La diferencia de$12$ veces cuanto mayor y$7$ veces menor es$36$. Encuentra los números.
La suma de$4$ veces mayor número y$3$ veces menor es$7$. La diferencia de$8$ veces cuanto mayor y$6$ veces menor es$10$. Encuentra los números.

Contestar

1. Los números enteros son$22$ y$32$.

3. Los números enteros son$8$ y$24$.

5. Los números enteros son$16$ y$58$.

7. Los dos números son$−\frac{1}{4}$ y$\frac{1}{4}$.

9. El número menor es$−4$ y el mayor es$\frac{2}{3}$.

Ejercicio$\PageIndex{6}$ Interest and Money Problems

Configura un sistema lineal y resuelve.

Un $$7,000$ principal se invierte en dos cuentas, una ganando$3$% de interés y otra ganando$7$% de interés. Si el interés total del año es $$262$, entonces ¿cuánto se invierte en cada cuenta?
Mary tiene su ahorro total de $$12,500$ en dos cuentas de CD diferentes. Un CD gana$4.4$% interés y otro gana$3.2$% interés. Si su interés total para el año es $$463$, entonces ¿cuánto tiene en cada cuenta de CD?
El$1,800$ ahorro de $ de Sally está en dos cuentas. Una cuenta gana$6$% de interés anual y la otra gana$3$%. Su interés total para el año es de $$93$. ¿Cuánto tiene en cada cuenta?
Joe tiene dos cuentas de ahorro por un total de $$4,500$. Una cuenta gana$3\frac{3}{4}$% de interés anual y la otra gana$2\frac{5}{8}$%. Si su interés total para el año es $$141.75$, entonces ¿cuánto hay en cada cuenta?
Millicent tiene $$10,000$ invertidos en dos cuentas. Para el año, gana $$535$ más en intereses de su cuenta de$7$% de fondos mutuos que de su$4$% CD. ¿Cuánto tiene en cada cuenta?
Una pequeña empresa tiene $$85,000$ invertidos en dos cuentas. Si la cuenta que gana$3$% de interés anual gana $$825$ más en intereses que la cuenta que gana$4.5$% de interés anual, entonces ¿cuánto se invierte en cada cuenta?
Jerry obtuvo un total de $$284$ en intereses simples de dos cuentas separadas. En una cuenta que gana$6$% de interés, Jerry invirtió $$1,000$ más del doble de la cantidad que invirtió en una cuenta ganando$4$%. ¿Cuánto invirtió en cada cuenta?
James obtuvo un total de $$68.25$ en intereses simples de dos cuentas separadas. En una cuenta que ganaba$2.6$% de interés, James invirtió la mitad de lo que hizo en la otra cuenta que ganaba$5.2$%. ¿Cuánto invirtió en cada cuenta?
Una caja registradora contiene $$10$ facturas y $$20$ facturas con un valor total de $$340$. Si hay$23$ facturas totales, entonces ¿cuántos de cada uno contiene el registro?
John pudo comprar una pizza por $$10.80$ con cuartos y diez minutos. Si usa$60$ monedas para comprar la pizza, entonces ¿cuántos de cada uno tenía?
Dennis cortó el césped de su vecino por un frasco de diez y cinco dólares. Al concluir el trabajo, contó las monedas y encontró que había$4$ menos del doble de monedas de diez centavos que de cinco centavos. El valor total de todas las monedas es de $$6.60$. ¿Cuántas de cada moneda tenía?
Dos familias compraron boletos para el gran partido de futbol. Una familia ordenó boletos$2$ para adultos y boletos para$3$ niños por un total de $$26.00$. Otra familia ordenó boletos$3$ para adultos y boletos$4$ infantiles por un total de $$37.00$. ¿Cuánto costó cada boleto de adulto?
Dos amigos encontraron playeras y pantalones cortos a la venta en un mercadillo. Uno compró$5$ camisas y$3$ pantalones cortos por un total de $$51.00$. El otro compró$3$ camisas y$7$ pantalones cortos por un total de $$80.00$. ¿Cuánto costaba cada camisa y cada par de pantalones cortos?
El lunes Joe compró$10$ tazas de café y$5$ donas para su oficina a un costo de $$16.50$. Resulta que las donas eran más populares que el café. Por ello, el martes compró$5$ tazas de café y$10$ donas por un total de $$14.25$. ¿Cuánto costaba cada taza de café?

Contestar

1. $$5,700$ al$3$% y $$1,300$ al$7$%

3. $$1,300$ al$6$% y $$500$ al$3$%

5. $$8,500$ al$7$% y $$1,500$ al$4$%

7. $$1,400$ al$4$% y $$3,800$ al$6$%

9. $12$decenas y$11$ veinte

11. $52$monedas de diez centavos y$28$ cinco centavos

13. Camisas: $$4.50$; pantalones cortos: $$9.50$

Ejercicio$\PageIndex{7}$ Mixture Problems

Configura un sistema lineal y resuelve.

Una solución de$15$% de ácido se va a mezclar con una solución de$25$% de ácido para producir$12$ galones de una solución de$20$% de ácido. ¿Cuánto de cada uno se necesita?
Una solución de alcohol contiene$12$% de alcohol y otra contiene$26$% de alcohol. ¿Cuánto de cada uno se debe mezclar para obtener$5$ galones de una solución de$14.8$% de alcohol?
Una enfermera desea obtener$40$ onzas de un$1.2$% de solución salina. ¿Cuánto de un$1$% de solución salina debe mezclar con un$2$% de solución salina para lograr el resultado deseado?
Un cliente ordenó$20$ libras de fertilizante que contiene$15$% de nitrógeno. Para llenar el pedido del cliente, ¿cuánto de las existencias$30$% de fertilizante nitrogenado se debe mezclar con el$10$% de fertilizante nitrogenado?
Un cliente ordenó$2$ libras de un producto mixto de maní que contenía$15$% de anacardos. El inventario consta de sólo dos mezclas que contienen$10$% y$30$% de anacardos. ¿Cuánto de cada tipo se debe mezclar para llenar el pedido?
¿Cuántas libras de maní puro se deben combinar con una mezcla de$20$% de maní para producir$10$ libras de una mezcla de$32$% de maní?
¿Cuánto líquido limpiador con$20$% de contenido de alcohol, debe mezclarse con agua para obtener una mezcla de$24$ -onza con$10$% de contenido de alcohol?
Un químico desea crear una solución de$32$ -onza con$12$% de contenido de ácido. Utiliza dos tipos de soluciones madre, una con$30$% de contenido de ácido y otra con$10$% de contenido de ácido. ¿Cuánto de cada uno necesita?
Una solución limpiadora concentrada que contiene$50$% de amoníaco se mezcla con otra solución que contiene$10$% de amoníaco. ¿Cuánto de cada uno se mezcla para obtener$8$ onzas de una fórmula limpiadora de$32$% de amoníaco?
Un concentrado de$50$% de jugo de frutas se puede comprar al por mayor. El mejor sabor se logra cuando se mezcla agua con el concentrado de tal manera que se obtenga una mezcla de$12$% de jugo de fruta. ¿Cuánta agua y concentrado se necesita para hacer una bebida de jugo de frutas de$50$ -onza?
Un concentrado$75$% anticongelante se va a mezclar con agua para obtener$6$ galones de una solución$25$% anticongelante. ¿Cuánta agua se necesita?
El azúcar puro se debe mezclar con una ensalada de frutas que contenga$10$% de azúcar para producir$48$ onzas de una ensalada que contenga$16$% de azúcar. ¿Cuánto azúcar puro se requiere?

Contestar

1. $6$galones de cada

3. $32$onzas del$1$% de solución salina y$8$ onzas del$2$% de solución salina

5. $1.5$libras de la mezcla de$10$% de anacardo y$0.5$ libras de la mezcla de$30$% de anacardo

7. $12$onzas de líquido de limpieza

9. $4.4$onzas de la solución de$50$% de amoníaco y$3.6$ onzas de la solución de$10$% de amoníaco

11. $4$galones

Ejercicio$\PageIndex{8}$ Uniform Motion Problems

Configura un sistema lineal y resuelve.

Un avión promedió$460$ millas por hora en un viaje con el viento detrás de él y$345$ millas por hora en el viaje de regreso contra el viento. Si el viaje total de ida y vuelta tomó$7$ horas, entonces ¿cuánto tiempo pasó el avión en cada tramo del viaje?
Las dos etapas de un viaje$330$ de una milla tardaron$5$ horas. La velocidad promedio para el primer tramo del viaje fue de$70$ millas por hora y la velocidad promedio para el segundo tramo del viaje fue de$60$ millas por hora. ¿Cuánto tiempo duró cada tramo del viaje?
Un ejecutivo viajó$1,200$ millas, parte en helicóptero y parte en jet privado. El jet promedió$320$ millas por hora mientras que el helicóptero promedió$80$ millas por hora. Si el viaje total tomó$4\frac{1}{2}$ horas, entonces ¿cuánto tiempo pasó en el jet privado?
Joe tomó dos autobuses en el viaje de$463$ -milla de San José a San Diego. El primer autobús promedió$50$ millas por hora y el segundo autobús pudo promediar$64$ millas por hora. Si el viaje total tardó$8$ horas, entonces ¿cuánto tiempo se pasó en cada autobús?
Billy navegó río abajo hasta la tienda general a una tasa promedio de$9$ millas por hora. Su tarifa promedio de piragüismo de regreso río arriba fue de$4$ millas por hora. Si el viaje total tardó$6\frac{1}{2}$ horas, entonces ¿cuánto tardó Billy en volver al viaje de regreso?
Dos hermanos condujeron los$2,793$ kilómetros de Los Ángeles a Nueva York. Uno de los hermanos, manejando de día, pudo promediar$70$ millas por hora, y el otro, manejando de noche, pudo promediar$53$ millas por hora. Si el viaje total tomó$45$ horas, entonces, ¿cuántas horas manejó cada hermano?
Un barco viajó$24$ millas río abajo en$2$ horas. El viaje de regreso duró el doble. ¿Cuál era la velocidad de la embarcación y la corriente?
Un helicóptero que vuele con el viento puede recorrer$525$ millas en$5$ horas. En el viaje de regreso, contra el viento, tomará$7$ horas. ¿Cuáles son las velocidades del helicóptero y del viento?
Un barco puede recorrer$42$ millas con la corriente aguas abajo en$3$ horas. Al regresar río arriba contra la corriente, el barco solo puede recorrer$33$ millas en$3$ horas. Encuentra la velocidad de la corriente.
Un avión ligero que vuela con el viento puede recorrer$180$ millas en$1\frac{1}{2}$ horas. El avión puede volar la misma distancia contra el viento en$2$ horas. Encuentra la velocidad del viento.

Contestar

1. El avión voló$3$ horas con el viento y$4$ horas contra el viento.

3. $3.5$horas

5. $4.5$horas

7. Embarcación:$9$ millas por hora; corriente:$3$ millas por hora

9. $1.5$millas por hora

Ejercicio$\PageIndex{9}$ Discussion Board

Redactar un problema de número o dinero que pueda resolverse con un sistema de ecuaciones propio y compartirlo en el tablero de discusión.
Componer un problema de mezcla que pueda resolverse con un sistema de ecuaciones propio y compartirlo en el tablero de discusión.
Componer un problema de movimiento uniforme que pueda resolverse con un sistema de ecuaciones propio y compartirlo en el tablero de discusión

Contestar

1. Las respuestas pueden variar

3. Las respuestas pueden variar

Search

Text Color

Text Size

Margin Size

Font Type

	Porcentaje	Monto
Sal	\(2\)%\(=0.02\)	\(0.02(20\)onzas)\(=0.4\) onzas
Agua	\(98\)%\(=0.98\)	\(0.98(20\)onzas)\(=19.6\) onzas