Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

5.5: Dividir polinomios

Última actualización

30 oct 2022
Guardar como PDF
- 5.4: Multiplicar polinomios
- 5.6: Exponentes negativos

Anonymous
LibreTexts

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Dividir por un monomio.
Dividir por un polinomio usando el algoritmo de división.
Dividir las funciones polinomiales.

Dividir por un polinomio

Recordemos la regla del cociente para los exponentes: si $x$ es distinto de cero $m$ y y $n$ son enteros positivos, entonces

$\frac{x^{m}}{x^{n}}=x^{m-n}$

Es decir, al dividir dos expresiones con la misma base, restar los exponentes. Esta regla se aplica al dividir un monomio por un monomio. En esta sección, asumiremos que todas las variables en el denominador son distintas de cero.

Ejemplo $\PageIndex{1}$

Dividir:

$\frac{28y^{3}}{7y}$ .

Solución:

Dividir los coeficientes y restar los exponentes de la variable $y$ .

$\begin{aligned} \frac{28y^{3}}{7y}&=\frac{28}{7}y^{3-1} \\ &=4y^{2} \end{aligned}$

Respuesta:

$4y^{2}$

Ejemplo $\PageIndex{2}$

Dividir:

$\frac{24x^{7}y^{5}}{8x^{3}y^{2}}$ .

Solución:

Divida los coeficientes y aplique la regla del cociente restando los exponentes de las bases similares.

$\begin{aligned} \frac{24x^{7}y^{5}}{8x^{3}y^{2}}&=\frac{24}{8}x^{7-3}y^{5-2} \\ &=3x^{4}y^{3} \end{aligned}$

Respuesta:

$3x^{4}y^{3}$

Al dividir un polinomio por un monomio, podemos tratar el monomio como un denominador común y romper la fracción usando la siguiente propiedad:

$\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}$

La aplicación de esta propiedad resulta en términos que pueden ser tratados como cocientes de monomios.

Ejemplo $\PageIndex{3}$

Dividir:

$\frac{−5x^{4}+25x^{3}−15x^{2}}{5x^{2}}$ .

Solución:

Romper la fracción dividiendo cada término en el numerador por el monomio en el denominador y luego simplificar cada término.

Respuesta:

$-x^{2}+5x-3\cdot 1$

Comprueba tu división multiplicando la respuesta, el cociente, por el monomio en el denominador, el divisor, para ver si obtienes el numerador original, el dividendo.

$\color{Cerulean}{\frac{dividend}{divisor}=quotient}$

$or$

$\color{Cerulean}{dividend=divisor\cdot quotient}$

$\begin{aligned} 5x^{2}\cdot (-x^{2}+5x-3) &=\color{Cerulean}{5x^{2}}\color{black}{\cdot (-x^{2})+}\color{Cerulean}{5x^{2}}\color{black}{\cdot 5x-}\color{Cerulean}{5x^{2}}\color{black}{\cdot 3} \\ &=-5x^{4}+25x^{3}-15x^{2}\quad\color{Cerulean}{\checkmark} \end{aligned}$

Ejemplo $\PageIndex{4}$

Dividir:

$\frac{9a^{4}b−7a^{3}b^{2}+3a^{2}b}{−3a^{2}b}$ .

Solución:

Respuesta:

$-3a^{2}+\frac{7}{3}ab-1$ . El cheque es opcional y se deja en manos del lector.

Ejercicio $\PageIndex{1}$

$(16x^{5}−8x^{4}+5x^{3}+2x^{2})÷(2x^{2})$ .

Contestar: $8x^{3}−4x^{2}+\frac{5}{2}x+1$

Dividir por un polinomio

La misma técnica esbozada para dividir por un monomio no funciona para polinomios con dos o más términos en el denominador. En esta sección, esbozaremos un proceso llamado división polinómica larga, que se basa en el algoritmo de división para números reales. En aras de la claridad, asumiremos que todas las expresiones en el denominador son distintas de cero.

Ejemplo $\PageIndex{5}$

Dividir:

$\frac{x^{3}+3x^{2}−8x−4}{x−2}$ .

Solución:

Aquí $x−2$ está el divisor y $x^{3}+3x^{2}−8x−4$ está el dividendo.

Paso 1: Para determinar el primer término del cociente, dividir el término principal del dividendo por el término principal del divisor.

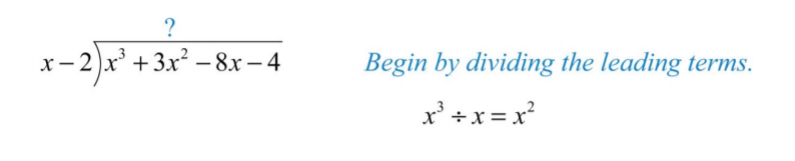Captura de pantalla (371) .png — Figura $\PageIndex{1}$

Paso 2: Multiplicar el primer término del cociente por el divisor, recordando distribuir, y alinear como términos con el dividendo.

Captura de pantalla (372) .png — Figura $\PageIndex{2}$

Paso 3: Restar la cantidad resultante del dividendo. Tenga cuidado de restar ambos términos.

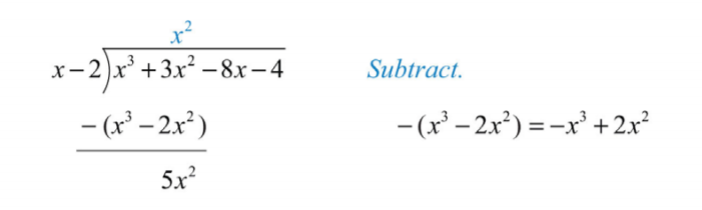Captura de pantalla (373) .png — Figura $\PageIndex{3}$

Paso 4: Derriba los términos restantes y repita el proceso del paso 1.

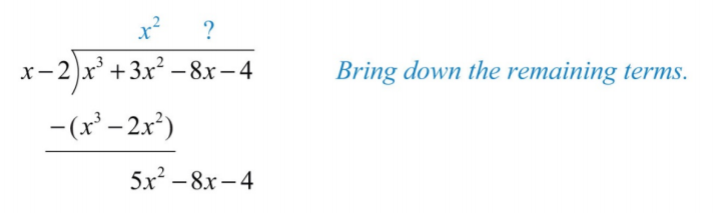Captura de pantalla (374) .png — Figura $\PageIndex{4}$

Observe que se elimina el plazo principal y que el resultado tiene un grado que es uno menos que el dividendo. El proceso completo se ilustra a continuación:

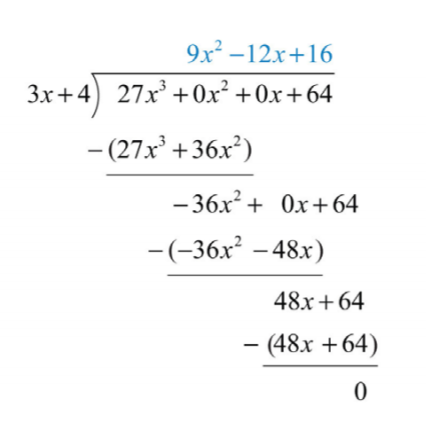Captura de pantalla (375) .png — Figura $\PageIndex{5}$

La división polinómica larga termina cuando el grado del resto es menor que el grado del divisor. Aquí está el resto $0$ . Por lo tanto, el binomio divide el polinomio de manera uniforme y la respuesta es el cociente que se muestra por encima de la línea de división.

$\frac{x^{3}+3x^{2}-8x-4}{x-2}=x^{2}+5x+2$

Para verificar la respuesta, multiplica el divisor por el cociente para ver si obtienes el dividendo:

$x^{3}+3x^{2}-8x-4=(x-2)(x^{2}+5x+2)$

Respuesta:

$x^{2}+5x+2$

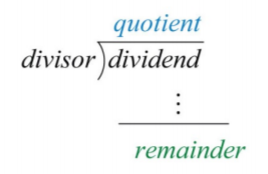
A continuación, demostramos el caso donde hay un resto distinto de cero.

Captura de pantalla (376) .png — Figura $\PageIndex{6}$

Al igual que con los números reales, la respuesta final suma la fracción donde el resto es el numerador y el divisor es el denominador al cociente. En general, al dividir tenemos

$\frac{dividend}{divisor}=\color{Cerulean}{quotient}\color{black}{+\frac{\color{OliveGreen}{remainder}}{divisor}}$

Si multiplicamos ambos lados por el divisor obtenemos

$dividend=\color{Cerulean}{quotient}\color{black}{\times\:divisor+}\color{OliveGreen}{remainder}$

Ejemplo $\PageIndex{6}$

Dividir:

$\frac{6x^{2}-5x+3}{2x-1}$

Solución:

Dado que el denominador es un binomio, comience por establecer la división polinómica larga.

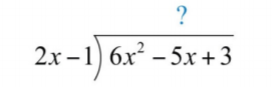Captura de pantalla (377) .png — Figura $\PageIndex{7}$

Para comenzar, determinar qué tiempos monomiales $2x−1$ resultan en un término líder $6x^{2}$ . Este es el cociente de los términos principales dados: $(6x^{2})÷(2x)=3x$ . $3x$ Multiplique por el divisor $2x−1$ y alinee el resultado con términos similares del dividendo.

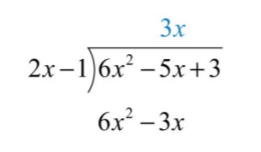Captura de pantalla (378) .png — Figura $\PageIndex{8}$

Restar el resultado del dividendo y derribar el plazo constante $+3$ .

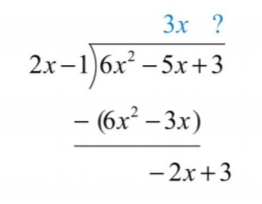Captura de pantalla (379) .png — Figura $\PageIndex{9}$

Restar elimina el término principal y $−5x−(−3x)=−5x+3x=−2x$ . El cociente de $−2x$ y $2x$ es $−1$ . Multiplica $2x−1$ por $−1$ y alinea el resultado.

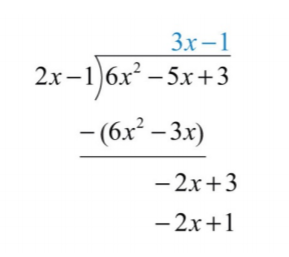Captura de pantalla (380) .png — Figura $\PageIndex{10}$

Restar de nuevo y notar que nos queda un resto.

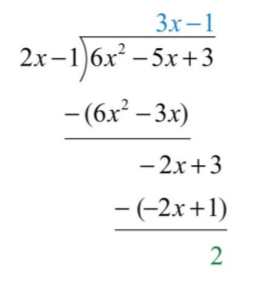Captura de pantalla (381) .png — Figura $\PageIndex{11}$

El término constante $2$ tiene grado $0$ , y así termina la división. Podemos escribir

$\frac{6x^{2}-5x+3}{2x-1}=\color{Cerulean}{3x-1}\color{black}{+\frac{\color{OliveGreen}{2}}{2x-1}}$

Respuesta:

$3x-1+\frac{2}{2x-1}$ . Para comprobar que este resultado es correcto, multiplicamos de la siguiente manera:

$\begin{aligned} \color{Cerulean}{quotient}\color{black}{\times\:divisor +}\color{OliveGreen}{remainder}&=\color{Cerulean}{(3x-1)}\color{black}{(2x-1)+}\color{OliveGreen}{2} \\ &=6x^{2}-3x-2x+1+2 \\ &=6x^{2}-5x+3 =dividend\quad\color{Cerulean}{\checkmark} \end{aligned}$

Ocasionalmente, algunos de los poderes de las variables parecen faltar dentro de un polinomio. Esto puede llevar a errores al alinear términos similares. Por lo tanto, al aprender por primera vez a dividir polinomios usando división larga, rellene los términos faltantes con coeficientes cero, llamados marcadores de posición.

Ejemplo $\PageIndex{7}$

Dividir:

$\frac{27x^{3}+64}{3x+4}$ .

Solución:

Observe que el binomio en el numerador no tiene términos con grado $2$ o $1$ . La división se simplifica si reescribimos la expresión con marcadores de posición:

$27x^{3}+64=27x^{3}\color{OliveGreen}{+0x^{2}+0x}\color{black}{+64}$

Configurar división larga polinomial:

Captura de pantalla (382) .png — Figura $\PageIndex{12}$

Comenzamos $27x^{3}÷3x=9x^{2}$ y trabajamos el resto del algoritmo de división.

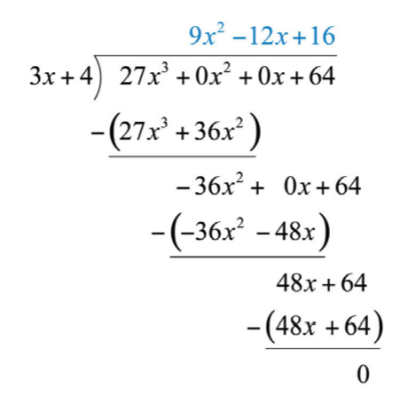Captura de pantalla (383) .png — Figura $\PageIndex{13}$

Respuesta:

$9x^{2}-12x+16$

Ejemplo $\PageIndex{8}$

Dividir:

$\frac{3x^{4}−2x^{3}+6x^{2}+23x−7}{x^{2}−2x+5}$ .

Solución:

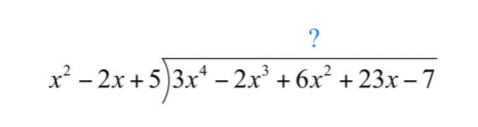Captura de pantalla (384) .png — Figura $\PageIndex{14}$

Iniciar el proceso dividiendo los términos principales para determinar el término principal del cociente $3x^{4}÷x^{2}=3x^{2}$ . Tenga cuidado de distribuir y alinear los términos similares. Continuar el proceso hasta que el resto tenga un grado menor que $2$ .

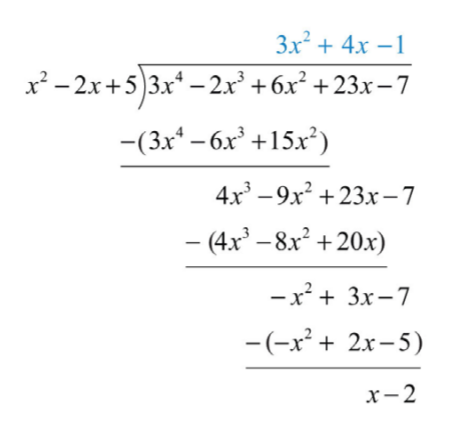Captura de pantalla (385) .png — Figura $\PageIndex{15}$

El resto es $x−2$ . Escribe la respuesta con el resto:

$\frac{3x^{4}-2x^{3}+6x^{2}+23x-7}{x^{2}-2x+5}=3x^{2}+4x-1+\frac{x-2}{x^{2}-2x+5}$

Respuesta:

$3x^{2}+4x-1+\frac{x-2}{x^{2}-2x+5}$

La división polinomial larga toma tiempo y práctica para dominar. Trabaje muchos problemas y recuerde que puede verificar sus respuestas multiplicando el cociente por el divisor (y agregando el resto si está presente) para obtener el dividendo.

Ejercicio $\PageIndex{2}$

Dividir:

$\frac{20x^{4}−32x^{3}+7x^{2}+8x−10}{5x−3}$ .

Contestar: $4x^{3}−4x^{2}−x+1−\frac{7}{5}x−3$

División de funciones polinomiales

Podemos usar la notación de función para indicar la división de la siguiente manera:

Mesa $\PageIndex{1}$
División de funciones:	$(f/g)(x)=\frac{f(x)}{g(x)}$

El cociente de dos funciones polinómicas no necesariamente tiene un dominio de todos los números reales. Los valores para $x$ que hacen la función en el denominador $0$ están restringidos del dominio. Esto se discutirá con más detalle en un momento posterior. Por ahora, supongamos que todas las funciones en el denominador son distintas de cero.

Ejemplo $\PageIndex{9}$

Calcular:

$(f/g)(x)$ dado $f(x)=6x^{5}−36x^{4}+12x^{3}−6x^{2}$ y $g(x)=−6x^{2}$ .

Solución:

La notación indica que debemos dividir:

$\begin{aligned} (f/g)(x)&=\frac{f(x)}{g(x)} \\ &=\frac{6x^{5}-36x^{4}+12x^{3}-6x^{2}}{-6x^{2}} \\ &=\frac{6x^{5}}{-6x^{2}}-\frac{36x^{4}}{-6x^{2}}+\frac{12x^{3}}{-6x^{2}}-\frac{6x^{2}}{-6x^{2}} \\ &=-1x^{5-2}+6x^{4-2}-2x^{3-2}+1x^{2-2} \\ &=-x^{3}+6x^{2}-2x+1 \end{aligned}$

Respuesta:

$(f/g)(x)=-x^{3}+6x^{2}-2x+1$

Ejemplo $\PageIndex{10}$

Calcular:

$(f/g)(−1)$ , dado $f(x)=−3x^{3}+7x^{2}−11x−1$ y $g(x)=3x−1$ .

Solución:

Primero, determinar $(f/g)(x)$ .

$(f/g)(x)=\frac{f(x)}{g(x)}=\frac{-3x^{3}+7x^{2}-11x-1}{3x-1}$

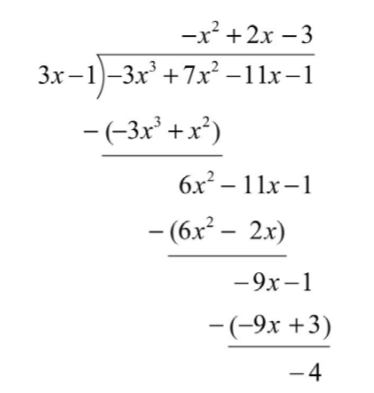Captura de pantalla (386) .png — Figura $\PageIndex{16}$

Por lo tanto,

$(f/g)(x)=-x^{2}+2x-3-\frac{4}{3x-1}$

Sustituto $−1$ de la variable $x$ .

Respuesta:

$(f/g)(-1)=-5$

Claves para llevar

Al dividir por un monomio, dividir todos los términos en el numerador por el monomio y luego simplificar cada término. Para simplificar cada término, dividir los coeficientes y aplicar la regla del cociente para los exponentes.
Al dividir un polinomio por otro polinomio, aplique el algoritmo de división.
Para verificar la respuesta después de dividir, multiplica el divisor por el cociente y suma el resto (si es necesario) para obtener el dividendo.
Es una buena práctica incluir marcadores de posición cuando se realiza la división polinómica larga.

Ejercicio $\PageIndex{3}$ Dividing by a Monomial

Dividir.

$\frac{81y^{5}}{9y^{2}}$
$\frac{36y^{9}}{9y^{3}}$
$\frac{52x^{2}y}{4xy}$
$\frac{24xy^{5}}{2xy^{4}}$
$\frac{25x^{2}y^{5}z^{3}}{5xyz}$
$\frac{−77x^{4}y^{9}z^{2}}{2x^{3}y^{3}z}$
$\frac{125a^{3}b^{2}c}{−10abc}$
$\frac{36a^{2}b^{3}c^{5}}{−6a^{2}b^{2}c^{3}}$
$\frac{9x^{2}+27x−3}{3}$
$\frac{10x^{3}−5x^{2}+40x−15}{5}$
$\frac{20x^{3}−10x^{2}+30x}{2x}$
$\frac{10x^{4}+8x^{2}−6x}{24x}$
$\frac{−6x^{5}−9x^{3}+3x}{−3x}$
$\frac{36a^{12}−6a^{9}+12a^{5}}{−12a^{5}}$
$\frac{−12x^{5}+18x^{3}−6x^{2}}{−6x^{2}}$
$\frac{−49a^{8}+7a^{5}−21a^{3}}{7a^{3}}$
$\frac{9x^{7}−6x^{4}+12x^{3}−x^{2}}{3x^{2}}$
$\frac{8x^{9}+16x^{7}−24x^{4}+8x^{3}}{−8x^{3}}$
$\frac{16a^{7}−32a^{6}+20a^{5}−a^{4}}{4a^{4}}$
$\frac{5a^{6}+2a^{5}+6a^{3}−12a^{2}}{3a^{2}}$
$\frac{−4x^{2}y^{3}+16x^{7}y^{8}−8x^{2}y^{5}}{−4x^{2}y^{3}}$
$\frac{100a^{10}b^{30}c^{5}−50a^{20}b^{5}c^{40}+20a^{5}b^{20}c^{10}}{10a^{5}b^{5}c^{5}}$
Encuentra el cociente de $−36x^{9}y^{7}$ y $2x^{8}y^{5}$ .
Encuentra el cociente de $144x^{3}y^{10}z^{2}$ y $−12x^{3}y^{5}z$ .
Encuentra el cociente de $3a^{4}−18a^{3}+27a^{2}$ y $3a^{2}$ .
Encuentra el cociente de $64a^{2}bc^{3}−16a^{5}bc^{7}$ y $4a^{2}bc^{3}$ .

Contestar

1. $9y^{3}$

3. $13x$

5. $5xy^{4}z^{2}$

7. $−\frac{25}{2}a^{2}b$

9. $3x^{2}+9x−1$

11. $10x^{2}−5x+15$

13. $2x^{4}+3x^{2}−1$

15. $2x^{3}−3x+1$

17. $3x^{5}−2x^{2}+4x−\frac{1}{3}$

19. $4a^{3}−8a^{2}+5a−\frac{1}{4}$

21. $−4x^{5}y^{5}+2y^{2}+1$

23. $−18xy^{2}$

25. $a^{2}−6a+9$

Ejercicio $\PageIndex{4}$ Dividing by a Polynomial

Dividir.

$(2x^{2}−5x−3)÷(x−3)$
$(3x^{2}+5x−2)÷(x+2)$
$(6x^{2}+11x+3)÷(3x+1)$
$(8x^{2}−14x+3)÷(2x−3)$
$\frac{x^{3}−x^{2}−2x−12}{x−3}$
$\frac{2x^{3}+11x^{2}+4x−5}{x+5}$
$\frac{2x^{3}−x^{2}−4x+3}{2x+3}$
$\frac{−15x^{3}−14x^{2}+23x−6}{5x−2}$
$\frac{14x^{4}−9x^{3}+22x^{2}+4x−1}{7x−1}$
$\frac{8x^{5}+16x^{4}−8x^{3}−5x^{2}−21x+10}{2x+5}$
$\frac{x^{2}+8x+17}{x+5}$
$\frac{2x^{2}−5x+5}{x−2}$
$\frac{6x^{2}−13x+9}{−2x+1}$
$\frac{−12x^{2}+x+1}{3x+2}$
$\frac{x^{3}+9x^{2}+19x+1}{x+4}$
$\frac{2x^{3}−13x^{2}+17x−11}{x−5}$
$\frac{9x^{3}−12x^{2}+16x−15}{3x−2}$
$\frac{3x^{4}−8x^{3}+5x^{2}−5x+9}{x−2}$
$(6x^{5}−13x^{4}+4x^{3}−3x^{2}+13x−2)÷(3x+1)$
$(8x^{5}−22x^{4}+19x^{3}−20x^{2}+23x−3)÷(2x−3)$
$\frac{5x^{5}+12x^{4}+12x^{3}−7x^{2}−19x+3}{x^{2}+2x+3}$
$\frac{6x^{5}−17x^{4}+5x^{3}+16x^{2}−7x−3}{2x^{2}−3x−1}$
$\frac{x^{5}+7x^{4}−x^{3}−7x^{2}−49 x+9}{x^{2}+7x−1}$
$\frac{5x^{6}−6x^{4}−4x^{2}+x+2}{5x^{2}−1}$
$\frac{x^{3}−27}{x−3}$
$\frac{8x^{3}+125}{2x+5}$
$(15x^{5}−9x^{4}−20x^{3}+12x^{2}+15x−9)÷(5x−3)$
$(2x^{6}−5x^{5}−4x^{4}+10x^{3}+6x^{2}−17x+5)÷(2x−5)$
$\frac{x^{5}−2x^{3}+3x−1}{x−1}$
$\frac{x^{4}−3x^{2}+5x−1}{3x+2}$
$\frac{a^{2}−4}{a+2}$
$\frac{a^{5}+1}{a^{5}+1}$
$\frac{a^{6}−1}{a−1}$
$\frac{x^{5}−1}{x−1}$
$\frac{x^{5}+x^{4}+6x^{3}+12x^{2}−4}{x^{2}+x−1}$
$\frac{50x^{6}−30x^{5}−5x^{4}+15x^{3}−5x+1}{5x^{2}−3x+2}$
$\frac{5x^{5}−15x^{3}+25x^{2}−5}{5x}$
$\frac{−36x^{6}+12x^{4}−6x^{2}}{6x^{2}}$
$\frac{150x^{5}y^{2}z^{15}−10x^{3}y^{6}z^{5}+4x^{3}y^{2}z^{4}}{10x^{3}y^{2}z^{5}}$
$\frac{27m^{6}+9m^{4}−81m^{2}+1}{9m^{2}}$
Dividir $3x^{6}−2x^{5}+27x^{4}−18x^{3}−6x^{2}+7x−10$ por $3x−2$ .
Dividir $8x^{6}+4x^{5}−14x^{4}−5x^{3}+x^{2}−2x−3$ por $2x+1$ .

Contestar

1. $2x+1$

3. $2x+3$

5. $x^{2}+2x+4$

7. $x^{2}−2x+1$

9. $2x^{3}−x^{2}+3x+1$

11. $x+3+\frac{2}{x+5}$

13. $−3x+5+\frac{4}{−2x+1}$

15. $x^{2}+5x−1+\frac{5}{x+4}$

17. $3x^{2}−2x+4−\frac{7}{3x−2}$

19. $2x^{4}−5x^{3}+3x^{2}−2x+5−\frac{7}{3x+1}$

21. $5x^{3}+2x^{2}−7x+1$

23. $x^{3}−7+\frac{2}{x^{2}+7x−1}$

25. $x^{2}+3x+9$

27. $3x^{4}−4x^{2}+3$

29. $x^{4}+x^{3}−x^{2}−x+2+\frac{1}{x−1}$

31. $a−2$

33. $a^{5}+a^{4}+a^{3}+a^{2}+a+1$

35. $x^{3}+7x+5+ \frac{2x+1}{x^{2}+x−1}$

37. $x^{4}−3x^{2}+5x−\frac{1}{x}$

39. $15x^{2}z^{10}−y^{4}+\frac{2}{5z}$

41. $x^{5}+9x^{3}−2x+1−\frac{8}{3x−2}$

Ejercicio $\PageIndex{5}$ Dividing Polynomial Functions

Calcular $(f/g)(x)$ , dadas las funciones.

$f(x)=40x^{8}$ y $g(x)=10x^{5}$
$f(x)=54x^{5}$ y $g(x)=9x^{3}$
$f(x)=12x^{2}+24x−15$ y $g(x)=2x+5$
$f(x)=−8x^{2}+30x−7$ y $g(x)=2x−7$
$f(x)=18x^{2}−36x+5$ y $g(x)=3x−5$
$f(x)=−7x^{2}+29x−6$ y $g(x)=7x−1$
$f(x)=10x^{3}−9x^{2}+27x−10$ y $g(x)=5x−2$
$f(x)=15x^{3}+28x^{2}−11x+56$ y $g(x)=3x+8$
$f(x)=2x^{4}+5x^{3}−11x^{2}−19x+20$ y $g(x)=x^{2}+x−5$
$f(x)=4x^{4}−12x^{3}−20x^{2}+26x−3$ y $g(x)=2x^{2}+2x−3$

Contestar

1. $(f/g)(x)=4x^{3}$

3. $(f/g)(x)=6x−3$

5. $(f/g)(x)=6x−2−\frac{5}{3x−5}$

7. $(f/g)(x)=2x^{2}−x+5$

9. $(f/g)(x)=2x^{2}+3x−4$

Ejercicio $\PageIndex{6}$ Dividing Polynomial Functions

Dado $f(x)=6x^{3}+4x^{2}−11x+3$ y $g(x)=3x−1$ , encuentra lo siguiente.

$(f/g)(x)$
$(f/g)(−1)$
$(f/g)(0)$
$(f/g)(1)$

Contestar

1. $(f/g)(x)=2x^{2}+2x−3$

3. $(f/g)(0)=−3$

Ejercicio $\PageIndex{7}$ Dividing Polynomial Functions

Dado $f(x)=5x^{3}−13x^{2}+7x+3$ y $g(x)=x−2$ , encuentra lo siguiente.

$(f/g)(x)$
$(f/g)(−3)$
$(f/g)(0)$
$(f/g)(7)$

Contestar

1. $(f/g)(x)=5x^{2}−3x+1+\frac{5}{x−2}$

3. $(f/g)(0)=−\frac{3}{2}$

Ejercicio $\PageIndex{8}$ Discussion Board Topics

¿Cómo se utiliza la propiedad distributiva al dividir un polinomio por un monomio?
Compara la división larga de números reales con la división larga polinomial. Proporcione un ejemplo de cada uno.

Contestar: 1. Las respuestas pueden variar

Dividir por un polinomio

Dividir por un polinomio

División de funciones polinomiales

Claves para llevar

Support Center

How can we help?