5.1: Reglas de Exponentes
- Page ID
- 110059
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Simplifica las expresiones usando las reglas de los exponentes.
- Simplifica las expresiones que involucran paréntesis y exponentes.
- Simplificar expresiones que implican\(0\) como exponente.
Producto, cociente y regla de potencia para exponentes
Si un factor se repite varias veces, entonces el producto se puede escribir en forma exponencial\(x_{n}\). El exponente entero positivo\(n\) indica el número de veces que la base\(x\) se repite como factor
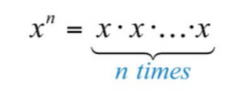.png)
Por ejemplo,
\(5^{4}=5\cdot 5\cdot 5\cdot 5\)
Aquí está la base\(5\) y el exponente está\(4\). Los exponentes a veces se indican con el símbolo de signo de contacto (^) que se encuentra en el teclado:\(5\) ^\(4 = 5*5*5*5\).
A continuación considere el producto de\(2^{3}\) y\(2^{5}\),
.png)
Ampliar la expresión usando la definición produce múltiples factores de la base, lo cual es bastante engorroso, particularmente cuando\(n\) es grande. Por ello, desarrollaremos algunas reglas útiles para ayudarnos a simplificar expresiones con exponentes. En este ejemplo, observe que podríamos obtener el mismo resultado sumando los exponentes.
\(2^{3}\cdot 2^{5}=2^{3+5}=2^{8}\)
En general, esto describe la regla del producto para exponentes. Si\(m\) y\(n\) son enteros positivos, entonces
\[x^{m}\cdot x^{n} = x^{m+n}\]
Es decir, al multiplicar dos expresiones con la misma base, sumar los exponentes.
Ejemplo\(\PageIndex{1}\)
Simplificar:\(10^{5}\cdot 10^{18}\).
Solución:
\(\begin{aligned} 10^{5}\cdot 10^{18}&=10^{5+18} \\ &=10^{23} \end{aligned}\)
Respuesta:
\(10^{23}\)
En el ejemplo anterior, observe que no multiplicamos la base 10 veces en sí misma. Al aplicar la regla del producto, agrega los exponentes y deja la base sin cambios.
Ejemplo\(\PageIndex{2}\)
Simplificar:\(x^{6}⋅x^{12}⋅x\).
Solución:
Recordemos que\(x\) se supone que la variable tiene un exponente de\(1: x=x^{1}\).
\(\begin{aligned} x^{6}\cdot x^{12}\cdot x &=x^{6}\cdot x^{12}\cdot x^{1} \\ &=x^{6+12+1} \\ &=x^{19} \end{aligned}\)
Respuesta:
\(x^{19}\)
La base podría ser cualquier expresión algebraica.
Ejemplo\(\PageIndex{3}\)
Simplificar:\((x+y)^{9} (x+y)^{13}\).
Solución:
Tratar la expresión\((x+y)\) como la base.
\(\begin{aligned} (x+y)^{9}(x+y)^{13}&=(x+y)^{9+13} \\ &=(x+y)^{22} \end{aligned}\)
Respuesta:
\((x+y)^{22}\)
La propiedad conmutativa de la multiplicación nos permite utilizar la regla de producto para exponentes para simplificar factores de una expresión algebraica.
Ejemplo\(\PageIndex{4}\)
Simplificar:\(2x^{8}y⋅3x^{4}y^{7}\).
Solución:
Multiplicar los coeficientes y sumar los exponentes de factores variables con la misma base.
\(\begin{aligned} 2x^{8}y\cdot 3x^{4}y^{7}&=2\cdot 3\cdot x^{8}\cdot x^{4}\cdot y^{1}\cdot y^{7} &\color{Cerulean}{Commutative\:property} \\ &=6\cdot x^{8+4}\cdot y^{1+7} &\color{Cerulean}{Power\:rule\:for\:exponents} \\ &=6x^{12}y^{8} \end{aligned}\)
Respuesta:
\(6x^{12}y^{8}\)
A continuación, desarrollaremos una regla para la división observando primero el cociente de\(2^{7}\) y\(2^{3}\).
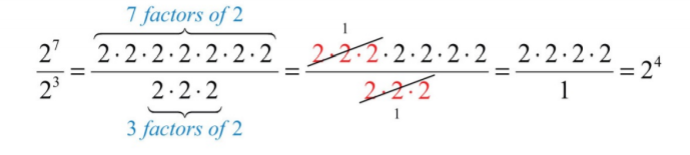.png)
Aquí podemos cancelar factores después de aplicar la definición de exponentes. Observe que el mismo resultado se puede obtener restando los exponentes.
\[\frac{2^{7}}{2^{3}}=2^{7-3}=2^{4} \nonumber\]
Esto describe la regla del cociente para los exponentes. Si\(m\) y\(n\) son enteros positivos y\(x≠0\), entonces
\[\frac{x^{m}}{x^{n}}=x^{m-n} \nonumber\]
En otras palabras, cuando divides dos expresiones con la misma base, restas los exponentes.
Ejemplo\(\PageIndex{5}\)
Simplificar:\(\frac{12y^{15}}{4y^{7}}\).
Solución:
Dividir los coeficientes y restar los exponentes de la variable\(y\).
\(\begin{aligned} \frac{12y^{15}}{4y^{7}}&=\frac{12}{4}\cdot y^{15-7}\\ &=3y^{8} \end{aligned}\)
Respuesta:
\(3y^{8}\)
Ejemplo\(\PageIndex{6}\)
Simplificar:\(\frac{20x^{10}(x+5)^{6}}{10x^{9}(x+5)^{2}}\)
Solución:
\(\begin{aligned} \frac{20x^{10}(x+5)^{6}}{10x^{9}(x+5)^{2}}&=\frac{20}{10}\cdot x^{10-9}\cdot (x+5)^{6-2} \\ &=2x^{1}(x+5)^{4} \end{aligned}\)
Respuesta:
\(2x(x+5)^{4}\)
Ahora elevar\(2^{3}\) a la cuarta potencia de la siguiente manera:
.png)
Después de escribir la base\(2^{3}\) como factor cuatro veces, ampliar para obtener\(12\) factores de\(2\). Podemos obtener el mismo resultado multiplicando los exponentes.
\((2^{3})^{^{4}} = 2^{3\cdot 4} = 2^{12}\)
En general, esto describe la regla de potencia para exponentes. Dados enteros positivos\(m\) y\(n\), entonces
\[(x^{m})^{^{n}}=x^{m\cdot n}\]
Es decir, al elevar una potencia a una potencia, multiplicar los exponentes.
Ejemplo\(\PageIndex{7}\)
Simplificar:\((y^{6})^{^{7}}=y^{6\cdot 7}\)
Solución:
\(\begin{aligned} (y^{6})^{^{7}}&=y^{6\cdot 7} \\ &=y^{42} \end{aligned}\)
Respuesta:
\(y^{42}\)
Para resumir, hemos desarrollado tres reglas muy útiles de exponentes que se utilizan ampliamente en álgebra. Si se dan enteros positivos\(m\) y\(n\), entonces
- Regla del producto:\[x^{m}\cdot x^{n}=x^{m+n}\]
- Regla del cociente:\[\frac{x^{m}}{x^{n}}=x^{m-n}, x\neq 0\]
- Regla de potencia:\[(x^{m})^{^{n}} = x^{m\cdot n}\]
Ejercicio\(\PageIndex{1}\)
Simplificar:\(y^{5}⋅(y^{4})^{^{6}}\).
- Contestar
-
\(y^{29}\)
Reglas de poder para productos y cocientes
Ahora consideramos elevar los productos agrupados a una potencia. Por ejemplo,
\(\begin{aligned} (xy)^{4} &= xy\cdot xy\cdot xy\cdot xy \\ &=x\cdot x\cdot x\cdot x\cdot y\cdot y\cdot y\cdot y\quad\color{Cerulean}{Commutative\:property} \\ &=x^{4}\cdot y^{4} \end{aligned}\)
Después de expandirnos, tenemos cuatro factores del producto\(xy\). Esto equivale a elevar cada uno de los factores originales a la cuarta potencia. En general, esto describe la regla de potencia para un producto. Si\(n\) es un entero positivo, entonces
\[(xy)^{n}=x^{n}y^{n}\]
Ejemplo\(\PageIndex{8}\)
Simplificar:\((2ab)^{7}=2^{7}a^{7}b^{7}\).
Solución:
Debemos aplicar el exponente\(7\) a todos los factores, incluido el coeficiente,\(2\).
\(\begin{aligned} (2ab)^{7}&=2^{7}a^{7}b^{7} \\ &=128a^{7}b^{7} \end{aligned}\)
Si un coeficiente se eleva a una potencia relativamente pequeña, entonces presentar el número real equivalente, como hicimos en este ejemplo:\(2^{7}=128\).
Respuesta:
\(128a^{7}b^{7}\)
En muchos casos, el proceso de simplificación de expresiones que involucran exponentes requiere el uso de varias reglas de exponentes.
Ejemplo\(\PageIndex{9}\)
Simplificar:\((3xy^{3})^{^{4}}\).
Solución:
\(\begin{aligned} (3xy^{3})^{^{4}}&=3^{4}\cdot x^{4}\cdot (y^{3})^{^{4}} &\color{Cerulean}{Power\:rule\:for\:products} \\ &=3^{4}x^{4}y^{3\cdot 4} &\color{Cerulean}{Power\:rule\:for\:exponents} \\ &=81x^{4}y^{12} \end{aligned}\)
Respuesta:
\(81x^{4}y^{12}\)
Ejemplo\(\PageIndex{10}\)
Simplificar:\((4x^{2}y^{5}z)^{^{3}}\).
Solución:
\(\begin{aligned} (4x^{2}y^{5}z)^{^{3}}&=4^{3}\cdot(x^{2})^{^{3}}\cdot (y^{5})^{^{3}}\cdot z^{3} \\ &=64x^{6}y^{15}z^{3} \end{aligned}\)
Respuesta:
\(64x^{6}y^{15}z^{3}\)
Ejemplo\(\PageIndex{11}\)
Simplificar:\([5(x+y)^{3}]^{^{3}}\)
Solución:
\(\begin{aligned} [5(x+y)^{3}]^{^{3}} &=5^{3}\cdot (x+y)^{9} \\ &=125(x+y)^{9} \end{aligned}\)
Respuesta:
\(125(x+y)^{9}\)
A continuación, consideremos un cociente elevado a una potencia.
\(\begin{aligned} \left( \frac{x}{y} \right) ^{4} &= \frac{x}{y}\cdot \frac{x}{y}\cdot \frac{x}{y}\cdot \frac{x}{y} \\ &=\frac{x\cdot x\cdot x\cdot x}{y\cdot y\cdot y\cdot y} \\ &=\frac{x^{4}}{y^{4}} \end{aligned}\)
Aquí obtenemos cuatro factores del cociente, lo que equivale al numerador y al denominador ambos elevados a la cuarta potencia. En general, esto describe la regla de poder para un cociente. Si\(n\) es un número entero positivo y\(y≠0\), entonces
\[\left( \frac{x}{y} \right) ^{n} = \frac{x^{n}}{y^{n}}\]
Es decir, dada una fracción elevada a una potencia, podemos aplicar ese exponente al numerador y al denominador. Esta regla requiere que el denominador sea distinto de cero. Haremos esta suposición para el resto de la sección.
Ejemplo\(\PageIndex{12}\)
Simplificar:\(\left(\frac{3a}{b} \right) ^{3}\)
Solución:
Primero, aplicar la regla de poder para un cociente y luego la regla de poder para un producto.
\(\begin{aligned} \left(\frac{3a}{b} \right) ^{3}&=\frac{(3a)^{3}}{b^{3}} &\color{Cerulean}{Power\:rule\:for\:a\:quotient} \\ &=\frac{3^{3}\cdot a^{3}}{b^{3}} &\color{Cerulean}{Power\:rule\:for\:a\:product} \\ &=\frac{27a^{3}}{b^{3}} \end{aligned}\)
Respuesta:
\(\frac{27a^{3}}{b^{3}}\)
En la práctica, a menudo combinamos estos dos pasos aplicando el exponente a todos los factores en el numerador y el denominador.
Ejemplo\(\PageIndex{13}\)
Simplificar:\(\left( \frac{ab^{2}}{2c^{3}} \right)^{5}\)
Solución:
Aplicar el exponente\(5\) a todos los factores en el numerador y el denominador.
\(\begin{aligned} \left( \frac{ab^{2}}{2c^{3}} \right)^{5}&=\frac{a^{5}(b^{2})^{^{5}}}{2^{5}(c^{3})^{^{5}}} \\ &=\frac{a^{5}b^{10}}{32c^{15}} \end{aligned}\)
Respuesta:
\(\frac{a^{5}b^{10}}{32c^{15}}\)
Ejemplo\(\PageIndex{14}\)
Simplificar:\(\left( \frac{5x^{5}(2x-1)^{4}}{3y^{7}} \right) ^{2}\)
Solución:
\(\begin{aligned} \left( \frac{5x^{5}(2x-1)^{4}}{3y^{7}} \right) ^{2} &=\frac{(5x^{5}(2x-1)^{4})^{2}}{(3y^{7})^{^{2}}} &\color{Cerulean}{Power\:rule\:for\:a\:quotient} \\ &=\frac{5^{2}\cdot (x^{5})^{^{2}}\cdot [(2x-1)^{4}]^{2}}{3^{2}\cdot (y^{7})^{^{2}}} &\color{Cerulean}{Power\:rule\:for\:products} \\ &=\frac{25x^{10}(2x-1)^{8}}{9y^{14}} &\color{Cerulean}{Power\:rule\:for\:exponents} \end{aligned}\)
Respuesta:
\(\frac{25x^{10}(2x-1)^{8}}{9y^{14}}\)
Es una buena práctica simplificar entre paréntesis antes de usar las reglas de poder; esto es consistente con el orden de las operaciones.
Ejemplo\(\PageIndex{15}\)
Simplificar:\(\left( \frac{-2x^{3}y^{4}z}{xy^{2}} \right)^{4}\)
Solución:
\(\begin{aligned} \left( \frac{-2x^{3}y^{4}z}{xy^{2}} \right)^{4}&=(-2\cdot x^{3-1}\cdot y^{4-2}\cdot z)^{4} &\color{Cerulean}{Simplify\:within\:the\:parentheses\:first.} \\ &=(-2\cdot x^{2}\cdot y^{2} \cdot z)^{4} &\color{Cerulean}{Apply\:the\:power\:rule\:for\:a\:product.} \\ &=(-2)^{4}\cdot (x^{2})^{^{4}}\cdot (y^{2})^{^{4}}\cdot z^{4}&\color{Cerulean}{Apply\:the\:power\:rule\:for\:exponents.} \\ &=16x^{8}y^{8}z^{4} \end{aligned}\)
Respuesta:
\(16x^{8}y^{8}z^{4}\)
Para resumir, hemos desarrollado dos nuevas reglas que son útiles cuando se utilizan símbolos de agrupación en conjunto con exponentes. Si se le da un entero positivo\(n\), donde\(y\) es un número distinto de cero, entonces
- Regla de potencia para un producto:\[(xy)^{n} = x^{n}y^{n}\]
- Regla de poder para un cociente:\[\left( \frac{x}{y} \right)^{n} = \frac{x^{n}}{y^{n}}\]
Ejercicio\(\PageIndex{2}\)
Simplificar:\(\left(\frac{4x^{2}(x-y)^{3}}{3yz^{5}} \right)^{3}\)
- Contestar
-
\(\frac{64x^{6}(x-y)^{9}}{27y^{3}z^{15}}\)
Cero como exponente
Usando la regla del cociente para exponentes, podemos definir lo que significa tener\(0\) como exponente. Considera el siguiente cálculo:
\ (\ color {cerúleo} {1}\ color {negro} {=\ frac {8} {8} =\ frac {2^ {3}} {2^ {3}} =2^ {3-3} =}\ color {cerúleo} {2^ {0}}
Ocho dividido por\(8\) es claramente igual a\(1\), y cuando se aplica la regla del cociente para exponentes, vemos que resulta un\(0\) exponente. Esto nos lleva a la definición de cero como exponente, donde\(x≠0\):
\[x^{0}=1\]
Es importante señalar que no\(0^{0}\) está definido. Si la base es negativa, entonces el resultado está quieto\(+1\). En otras palabras, cualquier base distinta de cero elevada a la\(0\) potencia se define como que sea\(1\). En los siguientes ejemplos, supongamos que todas las variables son distintas de cero.
Ejemplo\(\PageIndex{16}\)
Simplificar:
- \((-5)^{0}\)
- \(-5^{0}\)
Solución:
- Cualquier cantidad distinta de cero elevada a la\(0\) potencia es igual a\(1\).
\((-5)^{0}=1\)
B.En el ejemplo\(−5^{0}\), la base es\(5\), no\(−5\).
Respuesta:
- \(1\)
- \(-1\)
Ejemplo\(\PageIndex{17}\)
Simplificar:
\((5x^{3}y^{0}z^{2})^{^{2}}\).
Solución:
Es una buena práctica simplificar primero entre paréntesis.
\(\begin{aligned} (5x^{3}\color{Cerulean}{y^{0}}\color{black}{z^{2})^{^{2}}}&=(5x^{3}\cdot\color{Cerulean}{1}\color{black}{\cdot z^{2})^{2}} \\ &=(5x^{3}z^{2})^{2} \\ &=5^{2}x^{3\cdot 2}z^{2\cdot 2} \\ &=25x^{6}z^{4} \end{aligned}\)
Respuesta:
\(25x^{6}z^{4}\)
Ejemplo\(\PageIndex{18}\)
Simplificar:
\(\left( -\frac{8a^{10}b^{5}}{5c^{12}d^{14}} \right) ^{0}\).
Solución:
\(\left( -\frac{8a^{10}b^{5}}{5c^{12}d^{14}} \right) ^{0} =1\)
Respuesta:
\(1\)
Ejercicio\(\PageIndex{3}\)
Simplificar:
\(5x^{0}\)y\((5x)^{0}\)
- Contestar
-
\(5x^{0}=5\)y\((5x)^{0}=1\)
Claves para llevar
- Las reglas de los exponentes permiten simplificar expresiones que involucran exponentes.
- Al multiplicar dos cantidades con la misma base, agregue exponentes:\(x^{m}⋅x^{n}=x^{m+n}\).
- Al dividir dos cantidades con la misma base, restar exponentes:\(\frac{x^{m}}{x^{n}}=x^{m−n}\).
- Al elevar poderes a potencias, multiplicar exponentes:\((x^{m})^{^{n}}=x^{m⋅n}\).
- Cuando una cantidad agrupada que implica multiplicación y división se eleva a un poder, aplique ese poder a todos los factores en el numerador y el denominador:\((xy)^{n}=x^{n}y^{n}\) y\((\frac{x}{y})^{n}=\frac{x^{n}}{y^{n}}\).
- Cualquier cantidad distinta de cero elevada a la\(0\) potencia se define para que sea igual a\(1: x^{0}=1\).
Ejercicio\(\PageIndex{4}\) Product, Quotient, and Power Rule for Exponents
Escribe cada expresión usando forma exponencial.
- \((2x)(2x)(2x)(2x)(2x)\)
- \((−3y)(−3y)(−3y)\)
- \(−10⋅a⋅a⋅a⋅a⋅a⋅a⋅a\)
- \(12⋅x⋅x⋅y⋅y⋅y⋅y⋅y⋅y\)
- \(−6⋅(x−1)(x−1)(x−1)\)
- \((9ab)(9ab)(9ab)(a^{2}−b)(a^{2}−b)\)
- Contestar
-
1. \((2x)^{5}\)
3. \(-10a^{7}\)
5. \(-6(x-1)^{3}\)
Ejercicio\(\PageIndex{5}\) Product, Quotient, and Power Rule for Exponents
Simplificar.
- \(2^{7}⋅2^{5}\)
- \(3^{9}⋅3\)
- \(−2^{4}\)
- \((−2)^{4}\)
- \(−3^{3}\)
- \((−3)^{4}\)
- \(10^{13}⋅10^{5}⋅10^{4}\)
- \(10^{8}⋅10^{7}⋅10\)
- \(\frac{5^{12}}{5^{2}}\)
- \(\frac{10^{7}}{10^{10}}\)
- \(\frac{10^{12}}{10^{9}}\)
- \((7^{3})^{^{5}}\)
- \((4^{8})^{^{4}}\)
- \(10^{6}⋅(10^{5})^{^{4}}\)
- Contestar
-
1. \(2^{12}\)
3. \(−16\)
5. \(−27\)
7. \(10^{22}\)
9. \(5^{10}\)
11. \(10^{3}\)
13. \(4^{32}\)
Ejercicio\(\PageIndex{6}\) Product, Quotient, and Power Rule for Exponents
Simplificar.
- \((−x)^{6}\)
- \(a^{5}⋅(−a)^{2}\)
- \(x^{3}⋅x^{5}⋅x\)
- \(y^{5}⋅y^{4}⋅y^{2}\)
- \((a^{5})^{^{2}}⋅(a^{3})^{^{4}}⋅a\)
- \((x+1)^{4}(y^{5})^{^{4}}⋅y^{2}\)
- \((x+1)^{5}(x+1)^{8}\)
- \((2a−b)^{12}(2a−b)^{9}\)
- \(\frac{(3x-1)^{5}}{(3x-1)^{2}}\)
- \(\frac{(a-5)^{37}}{(a-5)^{13}}\)
- \(xy^{2}⋅x^{2}y\)
- \(3x^{2}y^{3}⋅7xy^{5}\)
- \(−8a^{2}b⋅2ab\)
- \(−3ab^{2}c^{3}⋅9a^{4}b^{5}c^{6}\)
- \(2a^{2}b^{4}c (−3abc)\)
- \(5a^{2}(b^{3})^{^{3}}c^{3}⋅(−2)2a^{3}(b^{2})^{^{4}}\)
- \(2x^{2}(x+y)^{5}⋅3x^{5}(x+y)^{4}\)
- \(−5xy^{6}(2x−1)^{6}⋅x^{5}y(2x−1)^{3}\)
- \(x^{2}y⋅xy^{3}⋅x^{5}y^{5}\)
- \(−2x^{10}y⋅3x^{2}y^{12}⋅5xy^{3}\)
- \(3^{2}x^{4}y^{2}z⋅3xy^{4}z^{4}\)
- \((−x^{2})^{^{3}}(x^{3})^{^{2}}(x^{4})^{^{3}}\)
- \(a^{10}⋅\frac{(a^{6})^{^{3}}}{a^{3}}\)
- \(\frac{10x^{9}(x^{3})^{^{5}}}{2x^{5}}\)
- \(\frac{a^{6}b^{3}}{a^{2}b^{2}}\)
- \(\frac{m^{10}n^{7}}{m^{3}n^{4}}\)
- \(\frac{20x^{5}y^{12}z^{3}}{10x^{2}y^{10}z}\)
- \(\frac{-24a^{16}b^{12}c^{3}}{6a^{6}b^{11}c}\)
- \(\frac{16x^{4}(x+2)^{3}}{4x(x+2)}\)
- \(\frac{50y^{2}(x+y)^{20}}{10y(x+y)^{17}}\)
- Contestar
-
1. \(x^{6}\)
3. \(x^{9}\)
5. \(a^{23}\)
7. \((x+1)^{13}\)
9. \((3x−1)^{3}\)
11. \(x^{3}y^{3}\)
13. \(−16a^{3}b^{2}\)
15. \(−6a^{3}b^{5}c^{2}\)
17. \(6x^{7}(x+y)^{9}\)
19. \(x^{8}y^{9}\)
21. \(27x^{5}y^{6}z^{5}\)
23. \(a^{25}\)
25. \(a^{4}b\)
27. \(2x^{3}y^{2}z^{2}\)
29. \(4x^{3}(x+2)^{2}\)
Ejercicio\(\PageIndex{7}\) Power Rules for Products and Quotients
Simplificar.
- \((2x)^{5}\)
- \((−3y)^{4}\)
- \((−xy)^{3}\)
- \((5xy)^{3}\)
- \((−4abc)^{2}\)
- \(\left(\frac{7}{2x} \right)^{2}\)
- \(-\left(\frac{5}{3y} \right)^{3}\)
- \((3abc)^{3}\)
- \(\left(\frac{-2xy}{3z} \right)^{4}\)
- \(\left(\frac{5y}{(2x-1)x}\right)^{3}\)
- \((3x^{2})^{^{3}}\)
- \((−2x^{3})^{^{2}}\)
- \((xy^{5})^{^{7}}\)
- \((x^{2}y^{10})^{^{2}}\)
- \(\left(\frac{3x^{2}}{y} \right)^{3}\)
- \((2x^{2}y^{3}z^{4})^{^{5}}\)
- \(\left(\frac{-7ab^{4}}{c^{2}} \right)^{2}\)
- \([x^{5}y^{4}(x+y)^{4}]^{5}\)
- \([2y(x+1)^{5}]^{3}\)
- \((ab^{3})^{^{3}}\)
- \(\left(\frac{5a^{2}}{3b} \right)^{4}\)
- \(\left(\frac{-2x^{3}}{3y^{2}} \right)^{2}\)
- \(\left(\frac{-x^{2}}{y^{3}} \right)^{3}\)
- \(\left(\frac{ab^{2}}{3c^{3}d^{2}} \right)^{4}\)
- \(\left(\frac{2x^{7}y}{(x-1)^{3}z^{5}} \right)^{6}\)
- \((2x^{4})^{^{3}}⋅(x^{5})^{^{2}}\)
- \((x^{3}y)^{^{2}}⋅(xy^{4})^{^{3}}\)
- \((−2a^{2}b^{3})^{^{2}}⋅(2a^{5}b)^{^{4}}\)
- \((−a^{2}b)^{3}(3ab^{4})^{4}\)
- \((2x^{3}(x+y)^{4})^{5}⋅(2x^{4}(x+y)^{2})^{3}\)
- \(\left(\frac{-3x^{5}y^{4}}{xy^{2}} \right)^{3}\)
- \(\left(\frac{-3x^{5}y^{4}}{xy^{2}} \right)^{2}\)
- \(\left(\frac{-25x^{10}y^{15}}{5x^{5}y^{10}} \right)^{3}\)
- \(\left(\frac{10x^{3}y^{5}}{5xy^{2}} \right)^{2}\)
- \(\left(\frac{-24ab^{3}}{6bc} \right)^{5}\)
- \(\left(\frac{-2x^{3}y^{16}}{x^{2}y} \right)^{2}\)
- \(\left(\frac{30ab^{3}}{3abc} \right)^{3}\)
- \(\left(\frac{3s^{3}t^{2}}{2s^{2}t} \right)^{3}\)
- \(\left(\frac{6xy^{5}(x+y)^{6}}{3y^{2}z(x+y)^{2}} \right)^{5}\)
- \(\left(\frac{-64a^{5}b^{12}c^{2}(2ab-1)^{14}}{32a^{2}b^{10}c^{2}(2ab-1)^{7}} \right)^{4}\)
- La probabilidad de lanzar una moneda justa y obtener\(n\) cabezas seguidas viene dada por la fórmula\(P=(12)^{n}\). Determinar la probabilidad, como porcentaje, de arrojar\(5\) cabezas seguidas.
- La probabilidad de rodar un solo dado justo\(n\) de seis lados y obtener las mismas caras hacia arriba en fila viene dada por la fórmula\(P=(16)^{n}\). Determinar la probabilidad, como porcentaje, de obtener el mismo boca arriba dos veces seguidas.
- Si cada lado de un cuadrado mide\(2x^{3}\) unidades, entonces determina el área en términos de la variable\(x\).
- Si cada borde de un cubo mide\(5x^{2}\) unidades, entonces determina el volumen en términos de la variable\(x\).
- Contestar
-
1. \(32x^{5}\)
3. \(−x^{3}y^{3}\)
5. \(16a^{2}b^{2}c^{2}\)
7. \(−\frac{125}{27y^{3}}\)
9. \(\frac{16x^{4}y^{4}}{81z^{4}}\)
11. \(27x^{6}\)
13. \(x^{7}y^{35}\)
15. \(\frac{27x^{6}}{y^{3}}\)
17. \(\frac{49a^{2}b^{8}}{c^{4}}\)
19. \(8y^{3}(x+1)^{15}\)
21. \(\frac{625a^{8}}{81b^{4}}\)
23. \(−\frac{x^{6}}{y^{9}}\)
25. \(\frac{64x^{42}y^{6}}{(x−1)^{18}z^{30}}\)
27. \(x^{9}y^{14}\)
29. \(−81a^{10}b^{19}\)
31. \(−27x^{12}y^{6}\)
33. \(−125x^{15}y^{15}\)
35. \(\frac{−1024a^{5}b^{10}}{c^{5}}\)
37. \(\frac{1000b^{6}}{c^{3}}\)
39. \(\frac{32x^{5}y^{15}(x+y)^{20}}{z^{5}}\)
41. \(3 \frac{1}{8}\)%
43. \(A=4x^{6}\)
Ejercicio\(\PageIndex{8}\) Zero Exponents
Simplificar. (Supongamos que las variables son distintas de cero.)
- \(7^{0}\)
- \((−7)^{0}\)
- \(−10^{0}\)
- \(−3^{0}⋅(−7)^{0}\)
- \(8675309^{0}\)
- \(5^{2}⋅3^{0}⋅2^{3}\)
- \(−3^{0}⋅(−2)^{2}⋅(−3)^{0}\)
- \(\frac{5x^{0}}{y^{2}}\)
- \((−3)^{2}x^{2}y^{0}z^{5}\)
- \(−3^{2}(x^{3})^{2}y^{2}(z^{3})^{0}\)
- \(2x^{3}y^{0}z⋅3x^{0}y^{3}z^{5}\)
- \(−3ab^{2}c^{0}⋅3a^{2}(b^{3}c^{2})^{0}\)
- \((−8xy^{2})^{0}\)
- \((2x^{2}y^{3})^{0}\)
- \(\frac{9x^{0}y^{4}}{3y^{3}}\)
- Contestar
-
1. \(1\)
3. \(−1\)
5. \(1\)
7. \(−4\)
9. \(9x^{2}z^{5}\)
11. \(6x^{3}y^{3}z^{6}\)
13. \(1\)
15. \(3y\)
Ejercicio\(\PageIndex{9}\) Discussion Board Topics
- René Descartes (1637) estableció el uso de la forma exponencial:\(a^{2}, a^{3}\), y así sucesivamente. Antes de esto, ¿cómo se denotaban los exponentes?
- Discutir los logros acreditados ante Al-Karismi.
- ¿Por qué es\(0^{0}\) undefined?
- Explique a un estudiante principiante por qué\(3^{4}⋅3^{2}≠9^{6}\).
- Contestar
-
1. Las respuestas pueden variar
3. Las respuestas pueden variar


