5.3: Sumando y restando polinomios
- Page ID
- 110066
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Agregar polinomios.
- Restar polinomios.
- Sumar y restar funciones polinómicas
Adición de polinomios
Recordemos que combinamos términos similares, o términos con la misma parte variable, como un medio para simplificar expresiones. Para ello, sumar los coeficientes de los términos para obtener un solo término con la misma parte variable. Por ejemplo,
\[5x^{2}+8x^{2}=13x^{2}\]
Observe que la parte variable\(x^{2}\),, no cambia. Esto, además de las propiedades conmutativas y asociativas de adición, nos permite agregar polinomios.
Ejemplo\(\PageIndex{1}\)
Agregar:
\(3x+(4x−5)\).
Solución:
La propiedad\(+(a+b)=a+b\), que se derivó usando la propiedad distributiva, nos permite eliminar los paréntesis para que podamos agregar términos similares.
Respuesta:
\(7x-5\)
Ejemplo\(\PageIndex{2}\)
Agregar:
\((3x^{2}+3x+5)+(2x^{2}−x−2)\).
Solución:
Elimine los paréntesis y luego combine términos similares.
Respuesta:
\(5x^{2}+2x+3\)
Ejemplo\(\PageIndex{3}\)
Agregar:
\((−5x^{2}y−2xy^{2}+7xy)+(4x^{2}y+7xy^{2}−3xy)\).
Solución:
Recuerda que las partes variables tienen que ser exactamente las mismas antes de poder sumar los coeficientes.
\(\begin{aligned} &(−5x^{2}y−2xy^{2}+7xy)+(4x^{2}y+7xy^{2}−3xy) \\ &=\color{Cerulean}{\underline{-5x^{2}y}}\color{black}{-}\color{OliveGreen}{\underline{\underline{2xy^{2}}}}\color{black}{+\underline{\underline{\underline{7xy}}}+}\color{Cerulean}{\underline{4x^{2}y}}\color{black}{+}\color{OliveGreen}{\underline{\underline{7xy^{2}}}}\color{black}{-\underline{\underline{\underline{3xy}}}} \\ &=-x^{2}y+5xy^{2}+4xy \end{aligned}\)
Respuesta:
\(-x^{2}y+5xy^{2}+4xy\)
Es práctica común presentar los términos de la expresión polinómica simplificada en orden descendente en función de su grado. En otras palabras, normalmente presentamos polinomios en forma estándar, con términos en orden de mayor a menor grado.
Ejemplo\(\PageIndex{4}\)
Agregar:
\((a−4a^{3}+a^{5}−8)+(−9a^{5}+a^{4}−7a+5+a^{3})\).
Solución:
Respuesta:
\(-8a^{5}+a^{4}-3a^{3}-6a-3\)
Ejercicio\(\PageIndex{1}\)
Agregar:
\((6−5x^{3}+x^{2}−x)+(x^{2}+x+6x^{3}−1)\).
- Contestar
-
\(x^{3}+2x^{2}+5\)
Restar polinomios
Al restar polinomios, vemos que los paréntesis se vuelven muy importantes. Recordemos que la propiedad distributiva nos permitió derivar lo siguiente:
\[-(a+b)=-a-b\]
En otras palabras, al restar una expresión algebraica, eliminamos los paréntesis restando cada término.
Ejemplo\(\PageIndex{5}\)
Restar:
\(10x−(3x+5)\).
Solución:
Reste cada término entre paréntesis y luego combine términos similares.
Respuesta:
\(7x-5\)
Restar una cantidad equivale a multiplicarla por\(−1\).
Ejemplo\(\PageIndex{6}\)
Restar:
\((3x^{2}+3x+5)−(2x^{2}−x−2)\).
Solución:
Distribuya el\(−1\), elimine los paréntesis y luego combine términos similares.
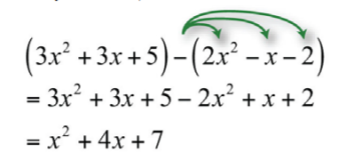.png)
Respuesta:
\(x^{2}+4x+7\)
Multiplicar los términos de un polinomio por\(−1\) los cambios de todos los signos.
Ejemplo\(\PageIndex{7}\)
Restar:
\((−5x^{3}−2x^{2}+7)−(4x^{3}+7x^{2}−3x+2)\).
Solución:
Distribuya el\(−1\), elimine los paréntesis y luego combine términos similares.
Respuesta:
\(-9x^{3}-9x^{2}+3x+5\)
Ejemplo\(\PageIndex{8}\)
Restar\(6x^{2}−3x−1\) de\(2x^{2}+5x−2\).
Solución
Dado que la resta no es conmutativa, debemos tener cuidado de establecer correctamente la diferencia. Primero, escribe la cantidad\((2x^{2}+5x−2)\); de esta, resta la cantidad\((6x^{2}−3x−1)\).
Respuesta:
\(-4x^{2}+8x-1\)
Ejemplo\(\PageIndex{9}\)
Simplificar:
\((2x^{2}−3x+5)−(x^{2}−3x+1)+(5x^{2}−4x−8)\).
Solución:
Aplica la propiedad distributiva, elimina los paréntesis y luego combina términos similares.
Respuesta:
\(6x^{2}-4x-4\)
Ejercicio\(\PageIndex{2}\)
Restar:
\((8x^{2}y−5xy^{2}+6)−(x^{2}y+2xy^{2}−1)\).
- Contestar
-
\(7x^{2}y-7xy^{2}+7\)
Sumando y restando funciones polinómicas
Utilizamos la notación de funciones para indicar la suma y resta de funciones de la siguiente manera:
| Adición de funciones: | \((f+g)(x)=f(x)+g(x)\) |
|---|---|
| Resta de funciones: | \((f-g)(x)=f(x)-g(x)\) |
Al usar la notación de funciones, tenga cuidado de agrupar toda la función y sumar o restar en consecuencia.
Ejemplo\(\PageIndex{10}\)
Calcular:
\((f+g)(x)\), dado\(f(x)=−x^{2}−3x+5\) y\(g(x)=3x^{2}+2x+1\).
Solución:
La notación\((f+g)(x)\) indica que debes agregar las funciones\(f(x)+g(x)\) y recopilar términos similares.
\(\begin{aligned} f(x)+g(x)&=(-x^{2}-3x+5)+(3x^{2}+2x+1) \\ &=-x^{2}-3x+5+3x^{2}+2x+1 \\ &=2x^{2}-x+6 \end{aligned}\)
Respuesta:
\((f+g)(x) = 2x^{2}-x+6\)
Ejemplo\(\PageIndex{11}\)
Calcular:
\((f−g)(x)\), dado\(f(x)=2x−3\) y\(g(x)=−2x^{2}+2x+5\).
Solución:
La notación\((f−g)(x)\) indica que debes restar las funciones\(f(x)−g(x)\):
Respuesta:
\((f-g)(x)=2x^{2}-8\)
Se nos puede pedir que evaluemos la suma o diferencia de dos funciones. Tenemos la opción de encontrar primero la suma o diferencia y usar la función resultante para evaluar la variable dada, o primero evaluar cada función y luego encontrar la suma o diferencia.
Ejemplo\(\PageIndex{12}\)
Calcular:
\((f−g)(5)\), dado\(f(x)=x^{2}+x−7\) y\(g(x)=4x+10\).
Solución:
Primero, encuentra\((f−g)(x)=f(x)−g(x)\).
Por lo tanto,
\((f-g)(x)=x^{2}-3x-17\)
A continuación, sustituya\(5\) la variable\(x\).
Respuesta:
\((f-g)(5)=-7\)
Solución alternativa:
Ya que\((f−g)(5)=f(5)−g(5)\), podemos encontrar\(f(5)\)\(g(5)\) y luego restar los resultados.
\(\begin{array}{c|c} {f(x)=x^{2}+x-7}&{g(x)=4x+10}\\{f(\color{OliveGreen}{5}\color{black}{)=(}\color{OliveGreen}{5}\color{black}{)^{2}+(}\color{OliveGreen}{5}\color{black}{)-7}}&{g(\color{OliveGreen}{5}\color{black}{)=4(}\color{OliveGreen}{5}\color{black}{)+10}}\\{=25+5-7}&{=20+10}\\{=23}&{=30} \end{array}\)
Por lo tanto, tenemos
Respuesta:
\((f-g)(5)=-7\)
Claves para llevar
- Al agregar polinomios, elimine los paréntesis asociados y luego combine términos similares.
- Al restar polinomios, distribuir\(−1\) y restar todos los términos antes de eliminar los paréntesis y combinar términos similares.
- La notación\((f+g)(x)\) indica que se agregan las funciones.
- La notación\((f−g)(x)\) indica que restas las funciones
Ejercicio\(\PageIndex{3}\) Addition of Polynomials
Agregar.
- \((2x+1)+(−x+7)\)
- \((−6x+5)+(3x−1)\)
- \((\frac{2}{3}x+\frac{1}{2})+(\frac{1}{3}x−2)\)
- \((\frac{1}{3}x−\frac{3}{4})+(\frac{5}{6}x+\frac{1}{8})\)
- \((2x+1)+(x−3)+(5x−2)\)
- \((2x−8)+(−3x^{2}+7x−5)\)
- \((x^{2}−3x+7)+(3x^{2}−8x−5)\)
- \((−5x^{2}−1+x)+(−x+7x^{2}−9)\)
- \((\frac{1}{2}x^{2}−\frac{1}{3}x+\frac{1}{6})+(−\frac{3}{2}x^{2}+\frac{2}{3}x−1)\)
- \((−\frac{3}{5}x2+\frac{1}{4}x−6)+(2x^{2}−\frac{3}{8}x+\frac{5}{2})\)
- \((x^{2}+5)+(3x^{2}−2x+1)+(x^{2}+x−3)\)
- \((a^{3}−a^{2}+a−8)+(a^{3}+a^{2}+6a−2)\)
- \((a^{3}−8)+(−3a^{3}+5a^{2}−2)\)
- \((4a^{5}+5a^{3}−a)+(3a^{4}−2a^{2}+7)\)
- \((2x^{2}+5x−12)+(7x−5)\)
- \((3x+5)+(x^{2}−x+1)+(x^{3}+2x^{2}−3x+6)\)
- \((6x^{5}−7x^{3}+x^{2}−15)+(x^{4}+2x^{3}−6x+12)\)
- \((1+7x−5x^{3}+4x^{4})+(−3x^{3}+5−x^{2}+x)\)
- \((x^{2}y^{2}−7xy+7)+(4x^{2}y^{2}−3xy−8)\)
- \((x^{2}+xy−y^{2})+(7x^{2}−5xy+2y^{2})\)
- \((2x^{2}+3xy−7y^{2})+(−5x^{2}−3xy+8y^{2})\)
- \((a^{2}b^{2}−100)+(2a^{2}b^{2}−3ab+20)\)
- \((ab^{2}−3a^{2}b+ab−3)+(−2a^{2}b+ab^{2}−7ab−1)\)
- \((10a^{2}b−7ab+8ab^{2})+(6a^{2}b−ab+5ab^{2})\)
- Encuentra la suma de\(2x+8\) y\(7x−1\).
- Encuentra la suma de\(13x−15\) y\(16x+110\).
- Encuentra la suma de\(x^{2}−10x+8\) y\(5x^{2}−2x−6\).
- Encuentra la suma de\(a^{2}−5a+10\) y\(−9a^{2}+7a−11\).
- Encuentra la suma de\(x^{2}y^{2}−xy+6\) y\(x^{2}y^{2}+xy−7\).
- Encuentra la suma de\(x^{2}−9xy+7y^{2}\) y\(−3x^{2}−3xy+7y^{2}\).
- Contestar
-
1. \(x+8\)
3. \(x−\frac{3}{2}\)
5. \(8x−4\)
7. \(4x^{2}−11x+2\)
9. \(−x^{2}+\frac{1}{3}x−\frac{5}{6}\)
11. \(5x^{2}−x+3\)
13. \(−2a^{3}+5a^{2}−10\)
15. \(2x^{2}+12x−17\)
17. \(6x^{5}+x^{4}−5x^{3}+x^{2}−6x−3\)
19. \(5x^{2}y^{2}−10xy−1\)
21. \(−3x^{2}+y^{2}\)
23. \(−5a^{2}b+2ab^{2}−6ab−4 \)
25. \(9x+7\)
27. \(6x^{2}−12x+2\)
29. \(2x^{2}y^{2}−1\)
Ejercicio\(\PageIndex{4}\) Subtraction of Polynomials
Restar.
- \((5x−3)−(2x−1)\)
- \((−4x+1)−(7x+10)\)
- \((\frac{1}{4}x−\frac{3}{4})−(\frac{3}{4}x+\frac{1}{8})\)
- \((−\frac{3}{5}x+\frac{3}{7})−(\frac{2}{5}x−\frac{3}{2})\)
- \((x^{2}+7x−5)−(4x^{2}−5x+1)\)
- \((−6x^{2}+3x−12)−(−6x^{2}+3x−12)\)
- \((−3x^{3}+4x−8)−(−x^{2}+4x+10)\)
- \((\frac{1}{2}x^{2}+\frac{1}{3}x−\frac{3}{4})−(\frac{3}{2}x^{2}−\frac{1}{6}x+\frac{1}{2})\)
- \((\frac{5}{9}x^{2}+\frac{1}{5}x−\frac{1}{3})−(\frac{1}{3}x^{2}+\frac{3}{10}x+\frac{5}{9})\)
- \((a^{3}−4a^{2}+3a−7)−(7a^{3}−2a^{2}−6a+9)\)
- \((3a^{3}+5a^{2}−2)−(a^{3}−a+8)\)
- \((5x^{5}+4x^{3}+x^{2}−6)−(4x^{4}−3x^{3}−x+3)\)
- \((3−5x−x^{3}+5x^{4})−(−5x^{3}+2−x^{2}−7x)\)
- \((x^{5}−6x^{3}+9x)−(4x^{4}+2x^{2}−5)\)
- \((2x^{2}y^{2}−4xy+9)−(3x^{2}y^{2}−3xy−5)\)
- \((x^{2}+xy−y^{2})−(x^{2}+xy−y^{2})\)
- \((2x^{2}+3xy−7y^{2})−(−5x^{2}−3xy+8y^{2})\)
- \((ab^{2}−3a^{2}b+ab−3)−(−2a^{2}b+ab^{2}−7ab−1)\)
- \((10a^{2}b−7ab+8ab^{2})−(6a^{2}b−ab+5ab^{2})\)
- \((10a^{2}b^{2}+5ab−6)−(5a^{2}b^{2}+5ab−6)\)
- Restar\(3x+1\) de\(5x−9\).
- Restar\(x^{2}−5x+10\) de\(x^{2}+5x−5\).
- Encuentra la diferencia de\(3x−7\) y\(8x+6\).
- Encuentra la diferencia de\(2x^{2}+3x−5\) y\(x^{2}−9\).
- El costo en dólares de producir tazas de café personalizadas con el logotipo de la compañía viene dado por la fórmula\(C=150+0.10x\), donde\(x\) está el número de tazas producidas. El ingreso por la venta de las tazas en la tienda de la compañía viene dado por\(R=10x−0.05x^{2}\), donde\(x\) está el número de unidades vendidas.
- Encuentra una fórmula para el beneficio. (beneficio = ingresos − costo)
- Encuentre el beneficio de producir y vender 100 tazas en la tienda de la compañía.
- El costo en dólares de producir sudaderas viene dado por la fórmula\(C=10q+1200\), donde\(C\) está el costo y\(q\) representa la cantidad producida. El ingreso generado por la venta de las sudaderas por $\(37\) cada una viene dado por\(R=37q\), donde\(q\) representa la cantidad vendida. Determinar el beneficio generado si se producen y venden\(125\) sudaderas.
- El radio exterior de una arandela es\(3\) multiplicado por el radio del orificio.
.png)
Figura\(\PageIndex{2}\)
a Derivar una fórmula para el área de la cara de la arandela.
b. ¿Cuál es el área de la arandela si el orificio tiene un diámetro de\(10\) milímetros? - Derive una fórmula para el área de superficie del siguiente sólido rectangular.
.png)
Figura\(\PageIndex{3}\)
- Contestar
-
1. \(3x−2\)
3. \(−\frac{1}{2}x−\frac{7}{8}\)
5. \(−3x^{2}+12x−6\)
7. \(−3x^{3}+x^{2}−18\)
9. \(\frac{2}{9}x^{2}−\frac{1}{10}x−\frac{8}{9}\)
11. \(2a^{3}+5a^{2}+a−10\)
13. \(5x^{4}+4x^{3}+x^{2}+2x+1\)
15. \(−x^{2}y^{2}−xy+14\)
17. \(7x^{2}+6xy−15y^{2}\)
19. \(4a^{2}b+3ab^{2}−6ab\)
21. \(2x−10\)
23. \(−5x−13 \)
25. a.\(P=−0.05x^{2}+9.9x−150\); b. $\(340\)
27. a.\(A=8πr^{2}\); b. milímetros\(628.32\) cuadrados
Ejercicio\(\PageIndex{5}\) Addition and Subtraction of Polynomial
Simplificar.
- \((2x+3)−(5x−8)+(x−7) \)
- \((3x−5)−(7x−11)−(5x+2) \)
- \((3x−2)−(4x−1)+(x+7) \)
- \((5x−3)−(2x+1)−(x−1) \)
- \((5x^{2}−3x+2)−(x^{2}+x−4)+(7x^{2}−2x−6) \)
- \((−2x^{3}+x^{2}−8)−(3x^{2}+x−6)−(2x−1)\)
- \((2x−7)−(x^{2}+3x−7)+(6x−1)\)
- \((6x^{2}−10x+13)+(4x^{2}−9)−(9−x^{2})\)
- \((a^{2}−b^{2})−(2a^{2}+3ab−4b^{2})+(5ab−1)\)
- \((a^{2}−3ab+b^{2})−(a^{2}+ b^{2})−(3ab−5)\)
- \((\frac{1}{2}x^{2}−\frac{3}{4}x+\frac{1}{4})−(\frac{3}{2}x−\frac{3}{4})+(\frac{5}{4}x−\frac{1}{2})\)
- \((\frac{9}{5}x^{2}−\frac{1}{3}x+2)−(\frac{3}{10}x^{2}−\frac{4}{5})−(x+\frac{5}{2})\)
- Contestar
-
1. \(−2x+4\)
3. \(6\)
5. \(11x^{2}−6x\)
7. \(−x^{2}+5x−1\)
9. \(−a^{2}+2ab+3b^{2}−1\)
11. \(12x^{2}−x+12\)
Ejercicio\(\PageIndex{6}\) Addition and Subtraction of Polynomial Functions
Encontrar\((f+g)(x)\) y\((f−g)(x)\), dadas las siguientes funciones.
- \(f(x)=4x−1\)y\(g(x)=−3x+1\)
- \(f(x)=−x+5\)y\(g(x)=2x−3\)
- \(f(x)=3x^{2}−5x+7\)y\(g(x)=−2x^{2}+5x−1\)
- \(f(x)=x^{3}+2x^{2}−6x+2\)y\(g(x)=2x^{3}+2x^{2}−5x−1\)
- \(f(x)=\frac{1}{2}x+\frac{1}{3}\)y\(g(x)=\frac{1}{5}x^{2}−\frac{3}{2}x+\frac{1}{6} \)
- \(f(x)=x^{2}−5x+\frac{1}{3}\)y\(g(x)=\frac{2}{3}x^{2}−x−\frac{1}{2}\)
- Contestar
-
1. \((f+g)(x)=x\)y\((f−g)(x)=7x−2\)
3. \((f+g)(x)=x^{2}+6\)y\((f−g)(x)=5x^{2}−10x+8\)
5. \((f+g)(x)=\frac{1}{5}x^{2}−x+\frac{1}{2}\)y\((f−g)(x)=−\frac{1}{5}x^{2}+2x+\frac{1}{6}\)
Ejercicio\(\PageIndex{7}\) Addition and Subtraction of Polynomial Functions
Dado\(f(x)=2x−3\) y\(g(x)=x^{2}+3x−1\), encuentra lo siguiente.
- \((f+g)(x) \)
- \((g+f)(x) \)
- \((f−g)(x) \)
- \((g−f)(x) \)
- \((g+g)(x) \)
- \((f+g)(3) \)
- \((f+g)(−2) \)
- \((f+g)(0) \)
- \((f−g)(0) \)
- \((f−g)(−2) \)
- \((g−f)(−2) \)
- \((g−f)(12)\)
- Contestar
-
1. \((f+g)(x)=x^{2}+5x−4\)
3. \((f−g)(x)=−x^{2}−x−2\)
5. \((g+g)(x)=2x^{2}+6x−2\)
7. \((f+g)(−2)=−10\)
9. \((f−g)(0)=−2\)
11. \((g−f)(−2)=4\)
Ejercicio\(\PageIndex{8}\) Addition and Subtraction of Polynomial Functions
Dado\(f(x)=5x^{2}−3x+2\) y\(g(x)=2x^{2}+6x−4\), encuentra lo siguiente.
- \((f+g)(x) \)
- \((g+f)(x) \)
- \((f−g)(x) \)
- \((g−f)(x) \)
- \((f+g)(−2) \)
- \((f−g)(−2) \)
- \((f+g)(0) \)
- \((f−g)(0)\)
- Contestar
-
1. \((f+g)(x)=7x^{2}+3x−2\)
3. \((f−g)(x)=3x^{2}−9x+6\)
5. \((f+g)(−2)=20\)
7. \((f+g)(0)=−2\)


