5.6: Exponentes negativos

Última actualización
Guardar como PDF

Page ID: 110047

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Simplifica las expresiones con exponentes enteros negativos.
Trabajo con notación científica.

Exponentes negativos

En esta sección, definimos lo que significa tener exponentes enteros negativos. Comenzamos con las siguientes fracciones equivalentes:

$\frac{1}{8}=\frac{4}{32}$

Observe que$4, 8$, y$32$ son todos los poderes de$2$. De ahí que podamos escribir$4=2^{2}, 8=2^{3}, and 32=2^{5}$.

$\frac{1}{2^{3}}=\frac{1}{8}=\frac{4}{32}=\frac{2^{2}}{2^{5}}$

Si el exponente del término en el denominador es mayor que el exponente del término en el numerador, entonces la aplicación de la regla del cociente para los exponentes da como resultado un exponente negativo. En este caso, tenemos lo siguiente:

$\color{Cerulean}{\frac{1}{2^{3}}}\color{black}{=\frac{1}{8}=\frac{4}{32}=\frac{2^{2}}{2^{5}}=2^{2-5}=}\color{Cerulean}{2^{-3}}$

Concluimos que$2^{−3}=\frac{1}{2}^{3}$. Esto es cierto en general y lleva a la definición de exponentes negativos. Dado cualquier número entero$n$ y$x≠0$, entonces

\[x^{-n}=\frac{1}{x^{n}}\]

Aquí$x≠0$ porque\ frac {1} {0}\) no está definido. Para mayor claridad, en esta sección, supongamos que todas las variables son distintas de cero.

Simplificar expresiones con exponentes negativos requiere que reescribamos la expresión con exponentes positivos.

Ejemplo$\PageIndex{1}$

Simplificar:

$10^{-2}$.

Solución:

$\begin{aligned} 10^{-2}&=\frac{1}{10^{2}} \\ &=\frac{1}{100} \end{aligned}$

Respuesta:

$\frac{1}{100}$

Ejemplo$\PageIndex{2}$

Simplificar:

$(-3)^{-1}$.

Solución:

$\begin{aligned} (-3)^{-1}&=\frac{1}{(-3)^{1}} \\ &=-\frac{1}{3} \end{aligned}$

Respuesta:

$-\frac{1}{3}$

Ejemplo$\PageIndex{3}$

Simplificar:

$\frac{1}{y^{-3}}$.

Solución:

$\begin{aligned} \frac{1}{y^{-3}} &=\frac{1}{\frac{1}{y^{3}}} \\ &=1\cdot \frac{y^{3}}{1} \\ &=y^{3} \end{aligned}$

Respuesta:

$y^{3}$

En este punto destacamos dos ejemplos muy importantes,

Captura de pantalla (387) .png — Figura$\PageIndex{1}$

Si la cantidad agrupada se eleva a un exponente negativo, entonces aplique la definición y escriba toda la cantidad agrupada en el denominador. Si no hay agrupación, entonces aplique la definición sólo a la base que precede al exponente.

Ejemplo$\PageIndex{4}$

Simplificar:

$(2ab)^{-3}$.

Solución:

Primero, aplique la definición de −3 como exponente y luego aplique el poder de una regla de producto.

$\begin{aligned} (2ab)^{-3} &=\frac{1}{(2ab)^{3}} \qquad\color{Cerulean}{Apply\:the\:negative\:exponent.} \\ &=\frac{1}{2^{3}a^{3}b^{3}} \qquad\color{Cerulean}{Apply\:the\:power\:rule\:for\:a\:product.} \\ &=\frac{1}{8a^{3}b^{3}} \end{aligned}$

Respuesta:

$\frac{1}{8a^{3}b^{3}}$

Ejemplo$\PageIndex{5}$

Simplificar:

$(-3xy^{3})^{-2}$.

Solución:

$\begin{aligned} (-3xy^{3})^{-2}&=\frac{1}{(-3xy^{3})^{2}} \\&=\frac{1}{(-3)^{2}x^{2}(y^{3})^{2}} \\ &=\frac{1}{9x^{2}y^{6}} \end{aligned}$

Respuesta:

$\frac{1}{9x^{2}y^{6}}$

Ejemplo$\PageIndex{6}$

Simplificar:

$\frac{x^{-3}}{y^{-4}}$.

Solución:

$\frac{x^{-3}}{y^{-4}}=\frac{\frac{1}{x^{3}}}{\frac{1}{y^{4}}}=\frac{1}{x^{3}}\cdot\frac{y^{4}}{1}=\frac{y^{4}}{x^{3}}$

Respuesta:

$\frac{y^{4}}{x^{3}}$

El ejemplo anterior sugiere una propiedad de cocientes con exponentes negativos. Si se le dan números enteros$m$ y$n$, dónde$x≠0$ y$y≠0$, entonces

\[\frac{x^{-n}}{y^{-m}}=\frac{y^{m}}{x^{n}}\]

En otras palabras, los exponentes negativos en el numerador se pueden escribir como exponentes positivos en el denominador, y los exponentes negativos en el denominador se pueden escribir como exponentes positivos en el numerador.

Ejemplo$\PageIndex{7}$

Simplificar:

$\frac{-2x^{-5}y^{3}}{z^{-2}}$.

Solución:

Cuídate con el coeficiente$−2$; reconoce que esta es la base y que el exponente es en realidad$+1:\: −2=(−2)^{1}$. De ahí que las reglas de los exponentes negativos no se apliquen a este coeficiente; déjalo en el numerador.

$\begin{aligned} \frac{-2x^{-5}y^{3}}{z^{-2}}&=\frac{-2\color{Cerulean}{x^{-5}}\color{black}{y^{3}}}{\color{OliveGreen}{z^{-2}}} \\ &=\frac{-2y^{3}\color{OliveGreen}{z^{2}}}{\color{Cerulean}{x^{5}}} \end{aligned}$

Respuesta:

$\frac{-2y^{3}z^{2}}{x^{5}}$

Ejemplo$\PageIndex{8}$

Simplificar:

$\frac{(-3x^{-4})^{-3}}{y^{-2}}$.

Solución:

$\begin{aligned} \frac{(-3x^{-4})^{-3}}{y^{-2}}&=\frac{(-3)^{-3}(x^{-4})^{-3}}{y^{-2}} &\color{Cerulean}{Apply\:the\:product\:to\:a\:power\:rule.} \\ &=\frac{(-3)^{-3}x^{12}}{y^{-2}} &\color{Cerulean}{Power\:rule} \\ &=\frac{x^{12}y^{2}}{(-3)^{3}} &\color{Cerulean}{Negative\:exponents} \\ &=\frac{x^{12}y^{2}}{-27} \\ &-\frac{x^{12}y^{2}}{27} \end{aligned}$

Respuesta:

$-\frac{x^{12}y^{2}}{27}$

Ejemplo$\PageIndex{9}$

Simplificar:

$\frac{(3x^{2})^{-4}}{(-2y^{-1}z^{3})^{-2}}$.

Solución:

$\begin{aligned} \frac{(3x^{2})^{-4}}{(-2y^{-1}z^{3})^{-2}}&=\frac{3^{-4}(x^{2})^{-4}}{(-2)^{-2}(y^{-1})^{-2}(z^{3})^{-2}} &\color{Cerulean}{Product\:to\:a\:power\:rule} \\ &=\frac{3^{-4}x^{-8}}{(-2)^{-2}y^{2}z^{-6}} &\color{Cerulean}{Power\:rule} \\ &=\frac{(-2)^{2}z^{6}}{3^{4}x^{8}y^{2}} &\color{Cerulean}{Negative\:exponents} \\&=\frac{4z^{6}}{81x^{8}y^{2}} \end{aligned}$

Respuesta:

$\frac{4z^{6}}{81x^{8}y^{2}}$

Ejemplo$\PageIndex{10}$

Simplificar:

$\frac{(5x^{2}y)^{3}}{x^{-5}y^{-3}}$.

Solución:

Primero, aplicar el poder de una regla de producto y luego la regla del cociente.

$\frac{(5x^{2})^{3}}{x^{-5}y^{-3}} = \frac{5^{3}x^{6}y^{3}}{x^{-5}y^{-3}}=5^{3}x^{6-(-5)}y^{3-(-3)}=5^{3}x^{6+5}y^{3+3}=125x^{11}y^{6}$

Respuesta:

$125x^{11}y^{6}$

Para resumir, tenemos las siguientes reglas para exponentes enteros negativos con bases distintas de cero:

Mesa$\PageIndex{1}$
Exponentes negativos:	$x^{-n}=\frac{1}{x^{n}}$
Cocientes con exponentes negativos:	$\frac{x^{-n}}{y^{-m}}=\frac{y^{m}}{x^{n}}$

Ejercicio$\PageIndex{1}$

Simplificar:

$\frac{(-5xy^{-3})^{-2}}{5x^{4}y^{-4}}$.

Contestar: $\frac{y^{10}}{125x^{6}}$

Notación Científica

Los números reales expresados en notación científica tienen la forma

$a\times 10^{n}$

donde$n$ es un número entero y$1≤a<10$. Esta forma es particularmente útil cuando los números son muy grandes o muy pequeños. Por ejemplo,

$\begin{array}{cc}{9,460,000,000,000,000m=9.46\times 10^{15}m}&{\color{Cerulean}{One\:light\:year}}\\{0.000000000025m=2.5\times 10^{-11}m}&{\color{Cerulean}{Radius\:of\:a\:hydrogen\:atom}} \end{array}$

Es engorroso escribir todos los ceros en ambos casos. La notación científica es una representación alternativa y compacta de estos números. El factor$10^{n}$ indica la potencia de$10$ multiplicar el coeficiente por convertir de nuevo a forma decimal:

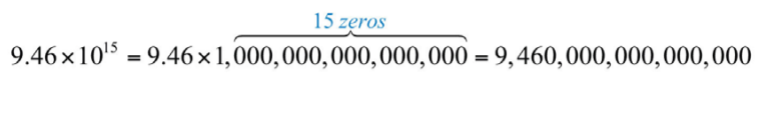Captura de pantalla (388) .png — Figura$\PageIndex{2}$

Esto equivale a mover el decimal en el coeficiente quince lugares a la derecha. Un exponente negativo indica que el número es muy pequeño:

Captura de pantalla (389) .png — Figura$\PageIndex{3}$

Esto equivale a mover el decimal en el coeficiente once lugares hacia la izquierda.

Convertir un número decimal a notación científica implica mover el decimal también. Considere todas las formas equivalentes de$0.00563$ con factores de los$10$ que siguen:

$\begin{aligned} 0.00563&=0.0563\times 10^{-1} \\ &=0.563\times 10^{-2} \\&\color{Cerulean}{=5.63\times 10^{-3}} \\&=56.3\times 10^{-4} \\&=563\times 10^{-5} \end{aligned}$

Si bien todos estos son iguales,$5.63×10^{−3}$ es la única forma que se considera que se expresa en notación científica. Esto se debe a que el coeficiente$5.63$ está entre$1$ y$10$ como lo exige la definición. Observe que podemos$5.63×10^{−3}$ volver a convertir a forma decimal, como cheque, moviendo el decimal a los tres lugares de la izquierda.

Ejemplo$\PageIndex{11}$

Escribir$1,075,000,000,000$ usando notación científica.

Solución:

Aquí contamos doce decimales a la izquierda del punto decimal para obtener el número$1.075$.

$1,075,000,000,000=1.075\times 10^{12}$

Respuesta:

$1.075\times 10^{12}$

Ejemplo$\PageIndex{12}$

Escribir$0.000003045$ usando notación científica.

Solución:

Aquí contamos seis decimales a la derecha para obtener$3.045$.

$0.000003045=3.045\times 10^{-6}$

Respuesta:

$3.045\times 10^{-6}$

A menudo necesitaremos realizar operaciones al usar números en notación científica. Todas las reglas de exponentes desarrolladas hasta ahora también se aplican a los números en notación científica.

Ejemplo$\PageIndex{13}$

Multiplicar:

$(4.36×10^{−5})(5.3×10^{12})$.

Solución:

Utilizar el hecho de que la multiplicación es conmutativa y aplicar la regla del producto para los exponentes.

$\begin{aligned} (4.36×10^{−5})(5.3×10^{12})&=(4.36\cdot 5.30)\times (10^{-5}\cdot 10^{12}) \\&=\color{Cerulean}{23.108}\color{black}{\times 10^{-5+12}} \\&=\color{Cerulean}{2.3108\times 10^{1}}\color{black}{\times 10^{7}} \\&=2.3108\times 10^{1+7} \\ &=2.3108\times 10^{8} \end{aligned}$

Respuesta:

$2.3108\times 10^{8}$

Ejemplo$\PageIndex{14}$

Dividir:

$(3.24\times 10^{8})\div (9.0\times 10^{-3})$.

Solución:

$\begin{aligned} \frac{(3.24\times 10^{8})}{(9.0\times 10^{-3})}&= \left( \frac{3.24}{9.0} \right) \times \left( \frac{10^{8}}{10^{-3}} \right) \\ &=0.36\times 10^{8-(-3)} \\&=\color{Cerulean}{0.36}\color{black}{\times 10^{8+3}} \\&=\color{Cerulean}{3.6\times 10^{-1}}\color{black}{\times 10^{11}} \\&=3.6\times 10^{-1+11} \\ &=3.6\times 10^{10} \end{aligned}$

Respuesta:

$3.6\times 10^{10}$

Ejemplo$\PageIndex{15}$

La velocidad de la luz es de aproximadamente$6.7×10^{8}$ millas por hora. Exprese esta velocidad en millas por segundo.

Solución:

Un análisis unitario indica que debemos dividir el número por$3,600$.

$\begin{aligned} 6.7\times 10^{8} \:mph &=\frac{6.7\times 10^{8}miles}{1\cancel{\color{red}{hour}}}\color{black}{\cdot}\left( \frac{1\cancel{\color{red}{hour}}}{60\cancel{\color{OliveGreen}{minutes}}} \right)\cdot \left( \frac{1\cancel{\color{OliveGreen}{minutes}}}{60 seconds} \right) \\&=\frac{6.7\times 10^{8}miles}{3600 seconds} \\&=\left(\frac{6.7}{3600} \right)\times 10^{8} \\ &\approx\color{Cerulean}{0.0019}\color{black}{\times 10^{8}} \qquad\color{Cerulean}{Rounded\:to\:two\:significant\:digits} \\ &=\color{Cerulean}{1.9\times 10^{-3}}\color{black}{\times 10^{8}} \\ &=1.9\times 10^{-3+8} \\ &=1.9\times 10^{5} \end{aligned}$

Respuesta:

La velocidad de la luz es de aproximadamente$1.9×10^{5}$ millas por segundo.

Ejemplo$\PageIndex{16}$

¿Por qué factor es el radio del sol mayor que el radio de la tierra?

$\begin{aligned} 6,300,000m &=6.3\times 10^{6}m\qquad\color{Cerulean}{Radius\:of\:Earth} \\ 700,000,000m &=7.0\times 10^{8}m\qquad\color{Cerulean}{Radius\:of\:the\:Sun} \end{aligned}$

Solución:

Queremos encontrar el número que cuando se multiplica por el radio de la tierra es igual al radio del sol.

$\begin{aligned}n\cdot \color{Cerulean}{radius\:of\:the\:Earth}&=\color{OliveGreen}{radius\:of\:the\:Sun} \\n&=\frac{\color{OliveGreen}{radius\:of\:the\:Sun}}{\color{Cerulean}{radius\:of\:the\:Earth}} \end{aligned}$

Por lo tanto,

$\begin{aligned} n&=\frac{7.0\times 10^{8}m}{6.3\times 10^{6}m} \\ &=\frac{7.0}{6.3}\times\frac{10^{8}}{10^{6}} \\ &\approx 1.1\times 10^{8-6} \\ &=1.1\times 10^{2} \\ &=110 \end{aligned}$

Ejercicio$\PageIndex{2}$

Dividir:

$(6.75\times 10^{-8})\div (9\times 10^{-17})$.

Contestar: $7.5\times 10^{8}$

Claves para llevar

Las expresiones con exponentes negativos en el numerador se pueden reescribir como expresiones con exponentes positivos en el denominador.
Las expresiones con exponentes negativos en el denominador se pueden reescribir como expresiones con exponentes positivos en el numerador.
Tenga cuidado de distinguir los coeficientes negativos de los exponentes negativos.
La notación científica es particularmente útil cuando se trabaja con números que son muy grandes o muy pequeños.

Ejercicio$\PageIndex{3}$ Negative Exponents

Simplificar. (Supongamos que las variables son distintas de cero.)

$5^{−1}$
$5^{−2}$
$(−7)^{−1}$
$−7^{−1}$
$\frac{1}{2}^{−3}$
$\frac{5}{3}^{−2}$
$(\frac{3}{5})^{−2}$
$(\frac{1}{2})^{−5}$
$(−\frac{2}{3})^{−4}$
$(−\frac{1}{3})^{−3}$
$x^{−4}$
$y^{−1}$
$3x^{−5}$
$(3x)^{−5}$
$\frac{1}{y^{−3}}$
$\frac{5}{2}x^{−1}$
$\frac{x^{−1}}{y^{−2}}$
$\frac{1}{(x−y)^{−4}}$
$\frac{x^{2}y^{−3}}{z^{−5}}$
$\frac{x}{y^{−3}}$
$(ab)^{−1}$
$\frac{1}{(ab)^{−1}}$
$−5x^{−3}y^{2}z^{−4}$
$\frac{3}{−2x^{3}y^{−5}z}$
$3x^{-4}y^{2}\cdot 2x^{-1}y^{3}$
$−10a^{2}b^{3}⋅2a^{−8}b^{−10}$
$(2a^{−3})^{−2}$
$(−3x^{2})^{−1}$
$(5a^{2}b^{−3}c)^{−2}$
$(7r^{3}s^{−5}t)^{−3}$
$(−2r^{2}s^{0}t^{−3})^{−1}$
$(2xy^{−3}z^{2})^{−3}$
$(−5a^{2}b^{−3}c^{0})^{4}$
$(−x^{−2}y^{3}z^{−4})^{−7}$
$(\frac{1}{2}x^{−3})^{−5}$
$(2xy^{2})^{−2}$
$(x^{2}y^{−1})^{−4}$
$(−3a^{2}bc^{5})^{−5}$
$(\frac{20x^{−3}y^{2}}{5yz^{−1}})^{−1}$
$(\frac{4r^{5}s^{−3}t^{4}}{2r^{3}st^{0}})^{−3}$
$(\frac{2xy^{3}z^{−1}}{y^{2}z^{3}})^{−3}$
$(−\frac{3a^{2}bc}{ab^{0}c^{4}})^{2}$
$(\frac{−xyz}{x^{4}y^{−2}z^{3}})^{−4}$
$(−\frac{125x^{−3}y^{4}z^{−5}}{5x^{2}y^{4}(x+y)^{3}})^{0}$
$(x^{n})^{−2}$
$(x^{n}y^{n})^{−2}$

Contestar

1. $\frac{1}{5}$

3. $−\frac{1}{7}$

5. $8$

7. $\frac{25}{9}$

9. $\frac{81}{16}$

11. $\frac{1}{x^{4}}$

13. $3x^{5}$

15. $y^{3}$

17. $\frac{y^{2}}{x}$

19. $\frac{x^{2}z^{5}}{y^{3}}$

21. $\frac{1}{ab}$

23. $\frac{−5y^{2}}{x^{3}z^{4}}$

25. $\frac{6y^{5}}{x^{5}}$

27. $\frac{a^{6}}{4}$

29. $\frac{b^{6}}{25a^{4}c^{2}}$

31. $−\frac{t^{3}}{2r^{2}}$

33. $\frac{625a^{8}}{b^{12}}$

35. $32x^{15}$

37. $\frac{y^{4}}{x^{8}}$

39. $\frac{x^{3}}{4yz}$

41. $\frac{z^{12}}{8x^{3}y^{3}}$

43. $\frac{x^{12}z^{8}}{y^{12}}$

45. $\frac{1}{x^{2n}}$

Ejercicio$\PageIndex{4}$ Negative Exponents

El valor en dólares de un nuevo reproductor MP3 se puede estimar utilizando la fórmula$V=100(t+1)^{−1}$, donde$t$ está el número de años después de la compra.

¿Cuánto valía el reproductor MP3 nuevo?
¿Cuánto valdrá el reproductor MP3 en el$1$ año?
¿Cuánto valdrá el reproductor MP3 en$4$ años?
¿Cuánto valdrá el reproductor MP3 en$9$ años?
¿Cuánto valdrá el reproductor MP3 en$99$ años?
De acuerdo con la fórmula, ¿alguna vez el MP3 será inútil? Explicar.

Contestar

1. $$100$

3. $$20$

5. $$1$

Ejercicio$\PageIndex{5}$ Scientific Notation

Convertir a un número decimal.

$9.3×10^{9}$
$1.004×10^{4}$
$6.08×10^{10}$
$3.042×10^{7}$
$4.01×10^{−7}$
$1.0×10^{−10}$
$9.9×10^{−3}$
$7.0011×10^{−5}$

Responder

1. $9,300,000,000$

3. $60,800,000,000$

5. $0.000000401$

7. $0.0099$

Ejercicio$\PageIndex{6}$ Scientific Notation

Reescribir usando notación científica.

$500,000,000$
$407,300,000,000,000$
$9,740,000$
$100,230$
$0.0000123$
$0.000012$
$0.000000010034$
$0.99071$

Responder

1. $5×10^{8}$

3. $9.74×10^{6}$

5. $1.23×10^{−5}$

7. $1.0034×10^{−8}$

Ejercicio$\PageIndex{7}$ Scientific Notation

Realizar las operaciones indicadas.

$(3×10^{5})(9×10^{4})$
$(8×10^{−22})(2×10^{−12})$
$(2.1×10^{−19})(3.0×10^{8})$
$(4.32×10^{7})(1.50×10^{−18})$
$9.12×10^{−9}3.2×10^{10}$
$1.15×10^{9}2.3×10^{−11}$
$1.004×10^{−8}2.008×10^{−14}$
$3.276×10^{25}5.2×10^{15}$
$59,000,000,000,000 × 0.000032$
$0.0000000000432 × 0.0000000000673$
$1,030,000,000,000,000,000 ÷ 2,000,000$
$6,045,000,000,000,000 ÷ 0.00000005$
La densidad poblacional de la tierra se refiere al número de personas por milla cuadrada de superficie terrestre. Si la superficie total de tierra en la tierra es de millas$5.751×10^{7}$ cuadradas y se estimó que la población en 2007 era de$6.67×10^{9}$ personas, entonces calcula la densidad poblacional de la tierra en ese momento.
En 2008 se estimó que la población de la ciudad de Nueva York era de$8.364$ millones de personas. La superficie total del terreno es de millas$305$ cuadradas. Calcular la densidad poblacional de la ciudad de Nueva York.
La masa de tierra es$5.97×10^{24}$ kilogramos y la masa de la luna es$7.35×10^{22}$ kilogramos. ¿Por qué factor es mayor la masa de la tierra que la masa de la luna?
La masa del sol es$1.99×10^{30}$ kilogramos y la masa de tierra es$5.97×10^{24}$ kilogramos. ¿Por qué factor es mayor la masa del sol que la masa de la tierra? Exprese su respuesta en notación científica.
El radio del sol es de$4.322×10^{5}$ millas y la distancia promedio de la tierra a la luna es de$2.392×10^{5}$ millas. ¿En qué factor es el radio del sol mayor que la distancia promedio de la tierra a la luna?
Un año luz,$9.461×10^{15}$ metros, es la distancia que la luz recorre al vacío en un año. Si se estima que la distancia a la estrella más cercana a nuestro sol, Próxima Centauri, es de$3.991×10^{16}$ metros, entonces calcula el número de años que tomaría luz recorrer esa distancia.
Se estima que hay alrededor de un$1$ millón de hormigas por persona en el planeta. Si la población mundial se estimó en$6.67$ mil millones de personas en 2007, entonces estime la población mundial de hormigas en ese momento.
El sol se mueve alrededor del centro de la galaxia en una órbita casi circular. La distancia desde el centro de nuestra galaxia hasta el sol es aproximadamente de años$26,000$ luz. ¿Cuál es la circunferencia de la órbita del sol alrededor de la galaxia en metros?
El agua pesa aproximadamente$18$ gramos por mol. Si un mol se trata de$6×10^{23}$ moléculas, entonces aproxima el peso de cada molécula de agua.
Un gigabyte es$1×10^{9}$ bytes y un megabyte es$1×10^{6}$ bytes. Si la canción promedio en formato MP3 consume alrededor de$4.5$ megabytes de almacenamiento, entonces ¿cuántas canciones caben en una tarjeta de memoria de$4$ -gigabyte?

Responder

1. $2.7×10^{10}$

3. $6.3×10^{−11}$

5. $2.85×10^{−19}$

7. $5×10^{5}$

9. $1.888×10^{9}$

11. $5.15×10^{11}$

13. Acerca de$116$ personas por milla cuadrada

15. $81.2$

17. $1.807$

19. $6.67×10^{15}$hormigas

21. $3×10^{−23}$gramos

Search

Text Color

Text Size

Margin Size

Font Type

Exponentes negativos:	\(x^{-n}=\frac{1}{x^{n}}\)
Cocientes con exponentes negativos:	\(\frac{x^{-n}}{y^{-m}}=\frac{y^{m}}{x^{n}}\)