6.7: Aplicaciones que involucran ecuaciones cuadráticas
( \newcommand{\kernel}{\mathrm{null}\,}\)
Objetivos de aprendizaje
- Configurar y resolver aplicaciones que involucren relaciones entre números reales.
- Configurar y resolver aplicaciones que involucren relaciones geométricas que involucran área y el teorema de Pitágoras.
- Configurar y resolver aplicaciones que involucren la altura de los proyectiles.
Problemas numéricos
Las configuraciones algebraicas de los problemas verbales que hemos encontrado anteriormente condujeron a ecuaciones lineales. Cuando traducimos las aplicaciones a configuraciones algebraicas en esta sección, las configuraciones conducen a ecuaciones cuadráticas. Al igual que antes, queremos evitar confiar en el método de “adivinar y verificar” para resolver aplicaciones. El uso del álgebra para resolver problemas simplifica el proceso y es más confiable.
Ejemplo6.7.1
Un entero es4 menos de dos veces otro entero, y su producto es96. Configurar una ecuación algebraica y resolverla para encontrar los dos enteros.
Solución:
Primero, identificar las variables. Evite dos variables usando la relación entre las dos incógnitas.
.png)
La frase clave, “su producto es”96, indica que debemos multiplicar y establecer el producto igual a96.
n⋅(2n−4)=96
Una vez que tenemos el problema traducido a una ecuación matemática, entonces resolvemos. En este caso, podemos resolver factorizando. El primer paso es escribir la ecuación en forma estándar:
n⋅(2n−4)=96Distributen.2n2−4n=96Subtract96frombothsides.2n2−4n−96=0
A continuación, factorizar completamente y establecer cada factor variable igual a cero.
2n2−4n−96=0FactorouttheGCF,2.2(n2−2n−48)=0Factortheresultingtrinomial.2(n+6)(n−8)=0Seteachvariablefactorequaltozero.
n+6=0orn−8=0n=−6n=8
El problema exige dos enteros cuyo producto es+96. El producto de dos números positivos es positivo y el producto de dos números negativos es positivo. De ahí que podamos tener dos conjuntos de soluciones. Utilízalo2n−4 para determinar los otros números enteros.
n=−6n=82n−4=2(−6)−42n−4=2(8)−4=−12−4=16−4=−16=12
Respuesta:
Dos conjuntos de enteros resuelven este problema: {8,12} y {−6,−16}. Observe eso(8)(12)=96 y(−6)(−16)=96; nuestras soluciones check out.
Con ecuaciones cuadráticas, a menudo obtenemos dos soluciones para lo desconocido identificado. Si bien puede darse el caso de que ambas sean soluciones a la ecuación, puede que no sean soluciones al problema. Si una solución no resuelve la aplicación original, entonces la ignoramos.
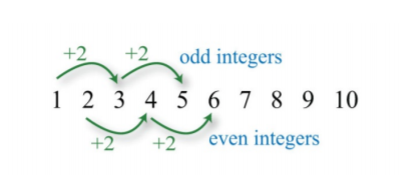
Recordemos que los enteros impares e impares consecutivos ambos están separados por dos unidades.
.png)
Ejemplo6.7.2
El producto de dos enteros impares positivos consecutivos es99. Encuentra los enteros.
Solución:
Letn representa el primer entero impar positivo.
Letn+2 representa el siguiente entero impar positivo.
La fase clave, “producto... es 99”, indica que debemos multiplicar y establecer el producto igual a99.
n⋅(n+2)=99
Reescribe la ecuación cuadrática en forma estándar y resuelve factorizando.
n2+2n=99n2+2n−99=0(n−9)(n+11)=0
n−9=0orn+11=0n=9n=−11
Porque el problema pide enteros positivos,n=9 es la única solución. Volver sustituto para determinar el siguiente entero impar.
n+2=9+2=11
Respuesta:
Los enteros impares positivos consecutivos son9 y11.
Ejemplo6.7.3
Dados dos enteros impares positivos consecutivos, el producto del mayor y el doble del menor es igual a70. Encuentra los enteros.
Solución:
Letn representa el número entero impar positivo más pequeño.
Letn+2 representa el siguiente entero impar positivo.
La frase clave “dos veces la más pequeña” se puede traducir a2n. La frase “producto... es 70” indica que debemos multiplicar esto por el entero impar más grande y establecer el producto igual a70.
(n+2)⋅2n=70
Resolver factorizando.
(n+2)⋅2n=70Distribute.2n2+4n=70Subtract70frombothsides.2n2+4n−70=0FactorouttheGCF,2.2(n2+2n−35)=0Factortheresultingtrinomial.2(n−5)(n+7)=0Seteachvariablefactorequaltozero.
n−5=0orn+7=0n=5n=−7
Porque el problema pide enteros positivos,n=5 es la única solución.
Volver a sustituir enn+2 para determinar el siguiente entero impar.
n+2=5+2=7
Respuesta:
Los enteros impares positivos son5 y7.
Ejercicio6.7.1
El producto de dos enteros pares positivos consecutivos es168. Encuentra los enteros.
- Contestar
-
Los enteros pares positivos son12 y14.
Problemas de Geometría
Cuando se trabaja con problemas de geometría, es útil dibujar una imagen. A continuación se presentan algunas fórmulas de área que se espera que conozca. (Recordemos esoπ≈3.14.)
| Área de un rectángulo: | A=l⋅w |
| Área de un cuadrado: | A=s2 |
| Área de un triángulo: | A=12bh |
| Área de un círculo: | A=πr2 |
Ejemplo6.7.4
El piso de una habitación rectangular tiene una longitud que es4 pies más del doble de su ancho. Si el área total del piso es de pies240 cuadrados, entonces encuentra las dimensiones del piso.
Solución:
.png)
Usa la fórmulaA=l⋅w y el hecho de que el área es de pies240 cuadrados para establecer una ecuación algebraica.
A=l⋅w240=(2w+4)⋅w
Resolver factorizando.
w−10=0orw+12=0w=10w=−12
En este punto tenemos dos posibilidades para el ancho del rectángulo. Sin embargo, dado que no se define un ancho negativo, elija la solución positiva,w=10. Volver sustituto para encontrar la longitud.
2w+4=2(10)+4=20+4=24
Respuesta:
El ancho es10 pies y el largo es24 pies.
Es importante incluir las unidades correctas en la presentación final de la respuesta. En el ejemplo anterior, no tendría mucho sentido decir que el ancho es10. Asegúrese de indicar que el ancho es10 pies.
Ejemplo6.7.5
La altura de un triángulo es3 pulgadas menos del doble de la longitud de su base. Si el área total del triángulo es de pulgadas7 cuadradas, entonces encuentra las longitudes de la base y la altura.
Solución:
.png)
Usa la fórmulaA=12bh y el hecho de que el área es pulgadas7 cuadradas para establecer una ecuación algebraica.
A=12b⋅h7=12b(2b−3)
Para evitar coeficientes fraccionarios, multiplique ambos lados por2 y luego reescriba la ecuación cuadrática en forma estándar.
Factor y luego establecer cada factor igual a cero.
2b−7=0orb+2=02b=7b=−2b=72
En este caso, desprecie la respuesta negativa; la longitud de la base es de72 pulgadas de largo. Se usa2b−3 para determinar la altura del triángulo.
Respuesta:
La base mide72=312 pulgadas y la altura es4 pulgadas.
Ejercicio6.7.1
La base de un triángulo es5 unidades menores al doble de la altura. Si el área es unidades75 cuadradas, entonces ¿cuál es la longitud de la base y la altura?
- Contestar
-
La altura es10 unidades y la base es15 unidades.
Recordemos que un triángulo rectángulo es un triángulo donde uno de los ángulos mide90°. El lado opuesto al ángulo recto es el lado más largo del triángulo y se llama hipotenusa. El teorema de Pitágoras nos da una relación entre las piernas y la hipotenusa de cualquier triángulo rectángulo, dondea yb son las longitudes de las piernas yc es la longitud de la hipotenusa:
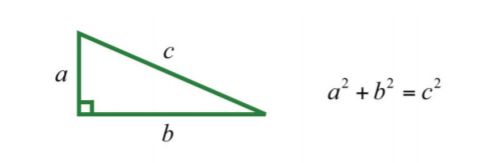.png)
Dadas ciertas relaciones, utilizamos este teorema a la hora de determinar las longitudes de los lados de los triángulos rectos.
Ejemplo6.7.6
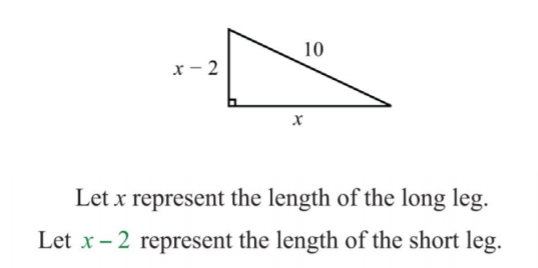
La hipotenusa de un triángulo rectángulo es10 pulgadas. Si la pierna corta es2 pulgadas menos que la pierna larga, entonces encuentra las longitudes de las piernas.
Solución:
.png)
Dado que la hipotenusa mide10 pulgadas, sustituya su valor en el teorema de Pitágoras y obtenga una ecuación cuadrática en términos dex.
a2+b2=c2(x−2)2+x2=102
Multiplicar y reescribir la ecuación en forma estándar.
(x−2)2+x2=102x2−4x+4+x2=1002x2−4x−96=0
Una vez que esté en forma estándar, factorizar y establecer cada factor variable igual a cero.
2x2−4x−96=02(x2−2x−48)=02(x+6)(x−8)=0
x+6=0orx−8=0x=−6x=8
Debido a que las longitudes no pueden ser negativas, despreciar la respuesta negativa. En este caso, la pierna larga mide8 pulgadas. Se usax−2 para determinar la longitud de la pierna corta.
x−2=8−2=6
Respuesta:
La pierna corta mide6 pulgadas y la pierna larga mide8 pulgadas.
Ejemplo6.7.7
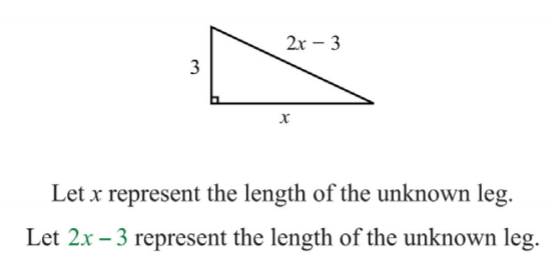
Una pata de un triángulo rectángulo mide3 centímetros. La hipotenusa del triángulo rectángulo mide3 centímetros menos del doble de la longitud de la pierna desconocida. Encuentra la medida de todos los lados del triángulo.
Solución:
.png)
Para establecer una ecuación algebraica, utilizamos el teorema de Pitágoras.
a2+b2=c232+x2=(2x−3)2
Resolver factorizando.
32+x2=(2x−3)29+x2=4x2−12x+90=3x2−12x0=3x(x−4)
3x=0orx−4=0x=0x=4
No tener en cuenta0. La longitud de la pierna desconocida es de4 centímetros. Utilizar2x−3 para determinar la longitud de la hipotenusa.
Respuesta:
Los lados del triángulo miden3 centímetros,4 centímetros y5 centímetros.
Ejercicio6.7.2
La hipotenusa de un triángulo rectángulo mide13 unidades. Si una pierna es2 unidades más del doble que la de la otra, entonces encuentra la longitud de cada pierna.
- Contestar
-
Las dos patas miden5 unidades y12 unidades.
Problemas de proyectiles
La altura de un objeto lanzado hacia arriba, ignorando los efectos de la resistencia al aire, se puede modelar con la siguiente fórmula:
height=−12gt2+v0t+s0
Usando la notación de funciones, que es más apropiada, tenemos
h(t)=−12gt2+v0t+s0
Con esta fórmula, la altura se puede calcular en cualquier momento dadot después de lanzar el objeto. Los coeficientes representan lo siguiente:
| −12g | La letrag representa la aceleración debida a la gravedad. |
| v0 | “v-nada” representa la velocidad inicial del objeto. |
| s0 | “s-nada” representa la altura inicial desde la que se lanza el objeto. |
Consideramos solo problemas donde la aceleración debida a la gravedad puede expresarse comog=32 pies/seg2. Por lo tanto, en esta sección el tiempo se medirá en segundos y la altura en pies. Sin embargo, ciertamente, la fórmula es válida usando unidades distintas a estas.
Ejemplo6.7.8
La altura de un proyectil lanzado hacia arriba a una velocidad de32 pies/segundo desde una altura de128 pies viene dada por la funciónh(t)=−16t2+32t+128. ¿Cuánto tiempo se tarda en golpear el suelo?
Solución:
Un método ineficiente para encontrar el tiempo para golpear el suelo es simplemente comenzar a adivinar a veces y evaluar. Para ello, construya un gráfico.
.png)
Usa la tabla para bosquejar la altura del proyectil a lo largo del tiempo.
.png)
Vemos que a los4 segundos, el proyectil choca contra el suelo. Tenga en cuenta que cuando esto ocurre, la altura es igual a0. Ahora necesitamos resolver este problema algebraicamente. Para encontrar la solución algebraicamente, use el hecho de que la altura es0 cuando el objeto choca con el suelo. Tenemos que encontrar el tiempo,t, cuándoh(t)=0.
h(t)=−16t2+32t+128↓0=−16t2+32t+128
Resolver la ecuación factorizando
0=−16t2+32t+1280=−16(t2−2t−8)0=−16(t−4)(t+2)
Ahora establece cada factor variable en cero.
t−4=0ort+2=0t=4t=−2
Como era de esperar, el proyectil golpea el suelo a lost=4 segundos. No tener en cuenta−2 como solución porque no se define el tiempo negativo.
Respuesta:
El proyectil golpea el suelo4 segundos después de ser lanzado.
Ejemplo6.7.9
La altura de cierto libro caído desde la parte superior de un edificio de144 pies viene dada porh(t)=−16t2+144. ¿Cuánto tiempo se tarda en golpear el suelo?
Solución:
Encuentra elt momento en que la alturah(t)=0.
0=−16t2+1440=−16(t2−9)0=−16(t+3)(t−3)
t+3=0ort−3=0t=−3t=3
Respuesta:
El libro tarda3 segundos en golpear el suelo cuando se cae desde lo alto de un edificio144 de pies.
Ejercicio6.7.3
La altura de un proyectil, disparado hacia arriba al aire desde el suelo, viene dada porh(t)=−16t2+80t. ¿Cuánto tiempo se tarda en volver a bajar al suelo?
- Contestar
-
Se tardarán 5 segundos en volver a bajar al suelo.
Claves para llevar
- Lo mejor es traducir un problema de palabras a una configuración matemática y luego resolverlo usando álgebra. Evite usar el método “adivinar y verificar” para resolver aplicaciones en esta sección.
- Al resolver aplicaciones, verifique que sus soluciones tengan sentido en el contexto de la pregunta. Por ejemplo, si deseas encontrar la longitud de la base de un triángulo, entonces ignorarías cualquier solución negativa.
- Es importante identificar cada variable y declarar en una oración lo que representa cada variable. A menudo es útil dibujar un cuadro.
Ejercicio6.7.4 Number Problems
Establecer una ecuación algebraica y luego resolver.
- Un entero es cinco veces otro. Si el producto de los dos enteros es80, entonces encuentra los enteros.
- Un entero es cuatro veces otro. Si el producto de los dos enteros es36, entonces encuentra los enteros.
- Un entero es uno más de cuatro veces otro. Si el producto de los dos enteros es39, entonces encuentra los enteros.
- Un entero es3 más que otro. Si el producto de los dos enteros es130, entonces encuentra los enteros.
- Un entero es2 menos de dos veces otro. Si el producto de los dos enteros es220, entonces encuentra los enteros.
- Un entero es3 más de dos veces otro. Si el producto de los dos enteros es90, entonces encuentra los enteros.
- Un entero es2 unidades más que otro. Si el producto de los dos enteros es igual a cinco veces mayor, entonces encuentra los dos enteros.
- Un entero positivo es1 menor que dos veces otro. Si el producto de los dos enteros es igual a quince veces el menor, entonces encuentra los dos enteros.
- Un entero positivo es3 más del doble de un entero positivo más pequeño. Si el producto de los dos enteros es igual a seis veces mayor, entonces encuentra los enteros.
- Un entero positivo es3 más que otro. Si el producto de los dos enteros es igual a doce veces el menor, entonces encuentra los enteros.
- Un entero es3 más que otro. Si el producto de los dos enteros es igual a2 más de cuatro veces su suma, entonces encuentra los enteros.
- Un entero es5 más que otro. Si el producto de los dos enteros es igual a2 más del doble de su suma, entonces encuentra los enteros.
- El producto de dos enteros pares positivos consecutivos es120. Encuentra los enteros.
- El producto de dos enteros impares positivos consecutivos es99. Encuentra los enteros.
- El producto de dos enteros positivos consecutivos es110. Encuentra los enteros.
- El producto de dos enteros positivos consecutivos es42. Encuentra los enteros.
- El producto de dos enteros impares positivos consecutivos es igual a1 menos de siete veces la suma de los enteros. Encuentra los enteros.
- El producto de dos enteros pares positivos consecutivos es igual a22 más de once veces la suma de los enteros. Encuentra los enteros.
- La suma de los cuadrados de dos enteros impares positivos consecutivos es74. Encuentra los enteros.
- La suma de los cuadrados de dos enteros pares positivos consecutivos es100. Encuentra los enteros.
- La suma de los cuadrados de dos enteros positivos consecutivos es265. Encuentra los enteros.
- La suma de los cuadrados de dos enteros positivos consecutivos es181. Encuentra los enteros.
- Para dos enteros impares positivos consecutivos, el producto del doble de menor y mayor es126. Encuentra los enteros.
- Para dos enteros pares positivos consecutivos, el producto de los más pequeños y dos veces más grandes es160. Encuentra los enteros.
- Contestar
-
1. {4,20} o {−4,−20}
3. 3,13
5. {11,20} o {−22,−10}
7. {5,7} o {−2,0}
9. 6,15
11. {7,10} o {−2,1}
13. 10,12
15. 10,11
17. 13,15
19. 5,7
21. 11,12
23. 7,9
Ejercicio6.7.5 Geometry Problems
Establecer una ecuación algebraica y luego resolver.
- El ancho de un rectángulo es7 pies menor que su longitud. Si el área del rectángulo es de pies170 cuadrados, entonces encuentra el largo y ancho.
- La longitud de un rectángulo es2 pies más que su ancho. Si el área del rectángulo es de pies48 cuadrados, entonces encuentra el largo y ancho.
- El ancho de un rectángulo es3 unidades menores que la longitud. Si el área es unidades70 cuadradas, entonces encuentra las dimensiones del rectángulo.
- El ancho de un rectángulo mide la mitad de la longitud. Si el área es de pies72 cuadrados, entonces encuentra las dimensiones del rectángulo.
- La longitud de un rectángulo es el doble que la de su ancho. Si el área del rectángulo es de pulgadas72 cuadradas, entonces encuentra el largo y ancho.
- La longitud de un rectángulo es tres veces mayor que su ancho. Si el área del rectángulo es de centímetros75 cuadrados, entonces encuentra el largo y ancho.
- La longitud de un rectángulo es2 pulgadas más que su ancho. El área del rectángulo es igual a12 pulgadas más de tres veces el perímetro. Encuentra el largo y ancho del rectángulo.
- La longitud de un rectángulo es3 metros más del doble del ancho. El área del rectángulo es igual a10 metros menos de tres veces el perímetro. Encuentra el largo y ancho del rectángulo.
- Se debe colocar un borde uniforme alrededor de una imagen de810 -pulgada por- pulgada. Si el área total incluyendo el borde debe ser de pulgadas224 cuadradas, entonces, ¿qué tan ancho debe ser el borde?
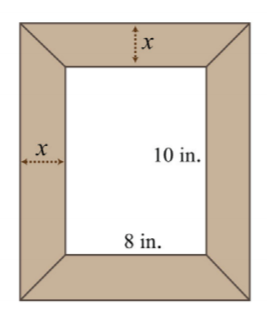.png)
10. Un borde de ladrillo de2 -pie se construye alrededor de una losa de cemento cuadrada. Si el área total, incluyendo el borde, es de pies121 cuadrados, entonces ¿cuáles son las dimensiones de la losa?
11. El área de un marco de fotos que incluye un borde2 de pulgadas de ancho es de pulgadas99 cuadradas. Si el ancho del área interior es2 pulgadas más que su longitud, entonces encuentre las dimensiones del área interior.
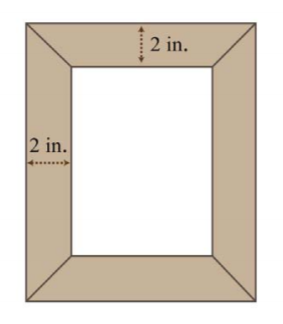.png)
12. Se puede hacer una caja cortando las esquinas y plegando los bordes de una hoja cuadrada de cartón. Se da una plantilla para una caja de cartón con una altura de2 pulgadas. ¿Cuál es la longitud de cada lado de la hoja de cartón si el volumen de la caja va a ser pulgadas50 cúbicas?
.png)
13. La altura de un triángulo es3 pulgadas más que la longitud de su base. Si el área del triángulo es de pulgadas44 cuadradas, entonces encuentra la longitud de su base y su altura.
14. La altura de un triángulo es4 unidades menor que la longitud de la base. Si el área del triángulo es unidades48 cuadradas, entonces encuentra la longitud de su base y altura.
15. La base de un triángulo es el doble que la de su altura. Si el área es de centímetros36 cuadrados, entonces encuentra la longitud de su base y altura.
16. La altura de un triángulo es tres veces la longitud de su base. Si el área es de pies7312 cuadrados, entonces encuentra la longitud de la base y la altura.
17. La altura de un triángulo es1 unidad más que la longitud de su base. Si el área es5 unidades más de cuatro veces la altura, entonces encuentra la longitud de la base y la altura del triángulo.
18. La base de un triángulo es4 multiplicada por la de su altura. Si el área es3 unidades más de cinco veces la altura, entonces encuentra la longitud de la base y la altura del triángulo.
19. La diagonal de un rectángulo mide5 pulgadas. Si el largo es1 pulgadas más que su ancho, entonces encuentre las dimensiones del rectángulo.
20. La diagonal de un rectángulo mide10 pulgadas. Si el ancho es2 pulgadas menor que el largo, entonces encuentra el área del rectángulo.
21. Si los lados de un triángulo rectángulo son enteros pares consecutivos, entonces ¿cuáles son sus medidas?
22. La hipotenusa de un triángulo rectángulo es13 unidades. Si la longitud de una pierna es2 más del doble que la otra, entonces ¿cuáles son sus longitudes?
23. La pata más corta de un triángulo rectángulo mide9 centímetros y la hipotenusa mide3 centímetros más que la pierna más larga. Encuentra la longitud de la hipotenusa.
24. La pierna larga de un triángulo rectángulo mide24 centímetros y la hipotenusa mide4 centímetros más tres veces la pierna corta. Encuentra la longitud de la hipotenusa.
- Contestar
-
1. Largo:17 pies; ancho:10 pies
3. Largo:10 unidades; ancho:7 unidades
5. Largo:12 pulgadas; ancho:6 pulgadas
7. Largo:14 pulgadas; ancho:12 pulgadas
9. 3pulgadas
11. 5pulgadas por7 pulgadas
13. Base:8 pulgadas; altura:11 pulgadas
15. Base:12 centímetros; altura:6 centímetros
17. Base:9 unidades; altura:10 unidades
19. 3pulgadas por4 pulgadas
21. 6unidades,8 unidades y10 unidades
23. 15centímetros
Ejercicio6.7.6 Projectile Problems
Establecer una ecuación algebraica y luego resolver.
- La altura de un proyectil lanzado hacia arriba a una velocidad de32 pies/segundo desde una altura de48 pies viene dada por la función\ (h (t) =−16t^ {2} +32t+48. ¿Cuánto tiempo tardará el proyectil en chocar contra el suelo?
- La altura de un proyectil lanzado hacia arriba a una velocidad de16 pies/segundo desde una altura de192 pies viene dada por la funciónh(t)=−16t2+16t+192. ¿Cuánto tiempo tardará en golpear el suelo?
- Un objeto se lanzó hacia arriba a una velocidad de64 pies/segundo desde una altura de80 pies. ¿Cuánto tiempo tardará el proyectil en chocar contra el suelo?
- Un objeto se lanzó hacia arriba a una velocidad de128 pies/segundo desde una altura de144 pies. ¿Cuánto tiempo tardará el proyectil en chocar contra el suelo?
- La altura de un objeto caído desde la parte superior de un edificio64 de pies viene dada porh(t)=−16t2+64. ¿Cuánto tiempo tardará el objeto en golpear el suelo?
- La altura de un objeto caído de un avión a1,600 pies viene dada porh(t)=−16t2+1,600. ¿Cuánto tiempo tardará el objeto en golpear el suelo?
- Un objeto se deja caer de una escalera a una altura de16 pies. ¿Cuánto tiempo tardará en golpear el suelo?
- Un objeto se deja caer de un edificio144 de pies. ¿Cuánto tiempo tardará en golpear el suelo?
- La altura de un proyectil, disparado hacia arriba al aire desde el suelo a128 pies/segundo, viene dada porh(t)=−16t2+128t. ¿Cuánto tiempo se tarda en volver a bajar al suelo?
- Un beisbol, arrojado al aire desde el suelo a32 pies/segundo, es dado porh(t)=−16t2+32t. ¿Cuánto tiempo se tarda en volver a bajar al suelo?
- ¿Cuánto tiempo tardará una pelota de béisbol lanzada al aire a48 pies/segundo en volver a bajar al suelo?
- Un balón de fútbol es levantado al aire a80 pies/segundo. Calcula cuánto tiempo va a colgar en el aire.
- Contestar
-
1. 3segundos
3. 5segundos
5. 2segundos
7. 1segundo
9. 8segundos
11. 3segundos
Ejercicio6.7.7 Discussion Board Topics
- Investigar y discutir la vida de Pitágoras.
- Si se duplican los lados de un cuadrado, entonces ¿en qué factor se incrementa el área? ¿Por qué?
- Diseña tu propio problema de geometría que involucre el área de un rectángulo o triángulo. Publica la pregunta y una solución completa en el panel de discusión.
- Escribe tu estrategia para configurar y resolver problemas verbales. Comparte tu estrategia en el panel de discusión.
- Contestar
-
1. Las respuestas pueden variar
3. Las respuestas pueden variar


