9.4: Directrices para resolver ecuaciones cuadráticas y aplicaciones

Última actualización
Guardar como PDF

Page ID: 110144

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Utilice el discriminante para determinar el número y tipo de soluciones a cualquier ecuación cuadrática.
Desarrollar una estrategia general para resolver ecuaciones cuadráticas.
Resolver aplicaciones que involucran ecuaciones cuadráticas.

Discriminante

Si se le da una ecuación cuadrática en forma estándar$ax^{2}+bx+c=0$,, donde a, b y c son números reales y a≠ 0, entonces las soluciones se pueden calcular usando la fórmula cuadrática:

Las soluciones son racionales, irracionales, o no reales. Podemos determinar el tipo y número de soluciones mediante el estudio del discriminante, la expresión dentro del radical,$b^{2}−4ac$. Si el valor de esta expresión es negativo, entonces la ecuación no tiene soluciones reales. Si el discriminante es positivo, entonces tenemos dos soluciones reales. Y si el discriminante es 0, entonces tenemos una solución real.

Ejemplo$\PageIndex{1}$

Determine el tipo y número de soluciones:

$x^{2}−10x+30=0$.

Solución:

Comenzamos por identificar a, b y c. Aquí

Sustituir estos valores por el discriminante y simplificar.

Dado que el discriminante es negativo, concluimos que no hay soluciones reales.

Respuesta:

No hay solución real

Si usamos la fórmula cuadrática en el ejemplo anterior, encontramos que un radical negativo detiene el proceso de simplificación y muestra que no hay una solución real.

Nota

Estudiaremos ecuaciones cuadráticas sin soluciones reales a medida que avancemos en nuestro estudio del álgebra.

Ejemplo$\PageIndex{2}$

Determine el tipo y número de soluciones:

$7x^{2}-10x+1=0$

Solución:

Aquí

Sustituir estos valores en el discriminante:

Dado que el discriminante es positivo, podemos concluir que existen dos soluciones reales.

Respuesta:

Dos soluciones reales

Si usamos la fórmula cuadrática en el ejemplo anterior, encontramos que un radicando positivo en la fórmula cuadrática conduce a dos soluciones reales.

Las dos soluciones reales son$\frac{5-3 \sqrt{2}}{7}$ y$\frac{5+3 \sqrt{2}}{7}$. Tenga en cuenta que estas soluciones son irracionales; podemos aproximar los valores en una calculadora.

Ejemplo$\PageIndex{3}$

Determine el tipo y número de soluciones:

$2x^{2}-7x-4=0$

Solución:

En este ejemplo,

Sustituir estos valores por el discriminante y simplificar.

Dado que el discriminante es positivo, concluimos que existen dos soluciones reales. Además, dado que el discriminante es un cuadrado perfecto, obtenemos dos soluciones racionales.

Respuesta:

Dos soluciones reales

Podríamos resolver la ecuación cuadrática anterior usando la fórmula cuadrática de la siguiente manera:

$\begin{array}{lll}{x=\frac{7-9}{4}} & {\text { or }} &{ x=\frac{7+9}{4}} \\ {x=\frac{-2}{4}} && {x=\frac{16}{4}} \\ {x=-\frac{1}{2}} && {x=4}\end{array}$

Nota

Si el discriminante es un cuadrado perfecto, entonces podríamos haber factorizado la ecuación original.

\ (2 x+1) (x-4) &=0\ end {alineado}\) </p">

$\begin{array}{rlr}{2 x+1} & {=0} & {\text { or }} & {x-4=0} \\ {2 x} & {=-1} & {} & {x=4} \\ {x} & {=-\frac{1}{2}}\end{array}$

Dada la condición especial donde el discriminante es 0, obtenemos una sola solución, una doble raíz.

Ejemplo$\PageIndex{4}$

Determine el tipo y número de soluciones:

$9x^{2}-6x+1=0$

Solución:

Aquí a=9, b=−6, y c=1, y tenemos

Dado que el discriminante es 0, concluimos que solo hay una solución real, una doble raíz.

Respuesta:

Una solución real

Dado que 0 es un cuadrado perfecto, podemos resolver la ecuación anterior factorizando.

$\begin{array}{rrr}{3 x-1=0} & {\text { or } \quad 3 x-1=0} \\ {3 x=1} & {3 x=1} \\ {x=\frac{1}{3}} & {x=\frac{1}{3}}\end{array}$

Aquí 1/3 es una solución que ocurre dos veces; es una raíz doble.

En resumen, si se da alguna ecuación cuadrática en forma estándar$ax^{2}+bx+c=0$,, donde a, b y c son números reales y a≠ 0, entonces tenemos lo siguiente:

Mesa$\PageIndex{1}$
Discriminante positivo:	$b^{2}-4ac >0$	Dos soluciones reales
Cero discriminante:	$b^{2}-4ac =0$	Una solución real
Discriminante negativo:	$b^{2}-4ac <0$	No hay solución real

Como veremos, conocer el número y el tipo de soluciones con anticipación nos ayuda a determinar qué método es el mejor para resolver una ecuación cuadrática.

Ejercicio$\PageIndex{1}$

Determinar el número y tipo de soluciones:

$3x^{2}-5x+4=0$

Contestar: No hay solución real

Lineamientos generales para resolver ecuaciones cuadráticas

Utilice los coeficientes de una ecuación cuadrática para ayudar a decidir qué método es el más adecuado para resolverlo. Si bien la fórmula cuadrática siempre funciona, a veces no es el método más eficiente. Dada cualquier ecuación cuadrática en forma estándar,$ax^{2}+bx+c=0$, siguen los lineamientos generales para determinar el método para resolverlo:

Si c = 0, entonces factorizar el GCF y resolver factorizando.
Si b = 0, entonces resuelve extrayendo las raíces.
Si a, b y c son todos distintos de cero, entonces determine el valor para el discriminante,$b^{2}−4ac$:
1. Si el discriminante es un cuadrado perfecto, entonces resuelva factorizando.
2. Si el discriminante no es un cuadrado perfecto, entonces resuelve usando la fórmula cuadrática.
3. Si el discriminante es positivo, obtenemos dos soluciones reales.
4. Si el discriminante es negativo, entonces no hay una solución real.

Ejemplo$\PageIndex{5}$

Resolver:

$15x^{2}-5x=0$

Solución:

En este caso, c = 0 y podemos resolver factorizando el GCF.

$\begin{array}{rlr}{5 x=0} & {\text { or } }&{ 3 x-1=0} \\ {x=0} && {3 x=1} \\ && {x=\frac{1}{3}}\end{array}$

Respuesta:

Las soluciones son 0 y$\frac{1}{3}$.

Ejemplo$\PageIndex{6}$

Resolver:

$3x^{2}-5=0$

Solución:

En este caso, b = 0 y podemos resolver extrayendo las raíces.

Respuesta:

Las soluciones son$\pm \frac{\sqrt{15}}{3}$

Ejemplo$\PageIndex{7}$

Resolver:

$9x^{2}-6x-7=0$

Solución:

Comience por identificar a, b y c como los coeficientes de cada término. Aquí

Sustituir estos valores en el discriminante y luego simplificar.

Dado que el discriminante es positivo y no un cuadrado perfecto, usa la fórmula cuadrática y espera dos soluciones reales.

Respuesta:

Las soluciones son$=\frac{1 \pm 2 \sqrt{2}}{3}$

Ejemplo$\PageIndex{8}$

Resolver:

$4 x(x-2)=-7$

Solución:

Comience por reescribir la ecuación cuadrática en forma estándar.

Aquí

Sustituir estos valores en el discriminante y luego simplificar.

Dado que el discriminante es negativo, las soluciones no son números reales.

Respuesta:

No hay solución real

Ejemplo$\PageIndex{9}$

Resolver:

$(3x+5)(3x+7)=6x+10$

Solución:

Comience por reescribir la ecuación cuadrática en forma estándar.

$\begin{aligned}(3 x+5)(3 x+7) &=6 x+10 \\ 9 x^{2}+21 x+15 x+35 &=6 x+10 \\ 9 x^{2}+36 x+35 &=6 x+10 \\ 9 x^{2}+30 x+25 &=0 \end{aligned}$

Sustituir a =9, b =30 y c =25 en el discriminante.

Dado que el discriminante es 0, resuelva factorizando y espere una solución real, una doble raíz.

$\begin{aligned} 9 x^{2}+30 x+25 &=0 \\(3 x+5)(3 x+5) &=0 \end{aligned}$

$\begin{array}{rrr}{3 x+5=0} & {\text { or } \quad 3 x+5=0} \\ {3 x=-5} & {3 x=-5} \\ {x=-\frac{5}{3}} & {x=-\frac{5}{3}}\end{array}$

Respuesta:

La solución es$-\frac{5}{3}$

Ejercicio$\PageIndex{2}$

Resolver:

$5x^{2}+2x-7=2x-3$

Contestar: $\pm\frac{2 \sqrt{5}}{5}$

Aplicaciones que involucran ecuaciones cuadráticas

En esta sección, las configuraciones algebraicas suelen consistir en una ecuación cuadrática donde las soluciones pueden no ser números enteros.

Ejemplo$\PageIndex{10}$

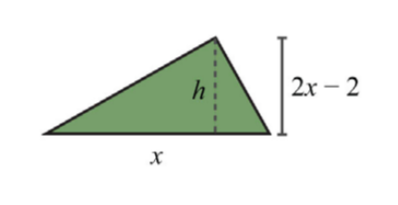
La altura de un triángulo es de 2 pulgadas menos del doble de la longitud de su base. Si el área total del triángulo es de 11 pulgadas cuadradas, entonces encuentra las longitudes de la base y la altura. Respuestas redondas a la centésima más cercana

Solución:

Captura de pantalla (231) .png — Figura$\PageIndex{1}$

Captura de pantalla (232) .png — Figura$\PageIndex{2}$

Usa la fórmula$A=\frac{1}{2}bh$ y el hecho de que el área sea de 11 pulgadas cuadradas para establecer una ecuación algebraica.

$\begin{array}{l}{A=\frac{1}{2} b \cdot h} \\ {\color{OliveGreen}{11}\color{black}{=}\frac{1}{2} x(\color{OliveGreen}{2 x-2}\color{black}{)}}\end{array}$

Para reescribir esta ecuación cuadrática en forma estándar, primero distribuya$\frac{1}{2}x$.

$\begin{array}{l}{11=\frac{1}{2} x(2 x-2)} \\ {11=x^{2}-x} \\ {0=x^{2}-x-11}\end{array}$

Utilice los coeficientes, a = 1, b = −1 y c = −11, para determinar el tipo de soluciones.

Dado que el discriminante es positivo, esperar dos soluciones reales.

En este problema, hacer caso omiso de la solución negativa y considerar sólo la solución positiva.

$x=\frac{1+3 \sqrt{5}}{2}$

Volver sustituto para encontrar la altura.

Respuesta:

La base mide$\frac{-1+3 \sqrt{5}}{2}\approx 3.85$ pulgadas y la altura es$-1+3 \sqrt{5} \approx 5.71$ pulgadas.

Ejemplo$\PageIndex{11}$

La suma de los cuadrados de dos enteros positivos consecutivos es 481. Encuentra los enteros.

Solución:

Que n represente el primer entero positivo.

Sea n+1 representar el siguiente entero positivo.

La configuración algebraica sigue:

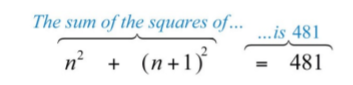Captura de pantalla (233) .png — Figura$\PageIndex{3}$

Reescribir la ecuación cuadrática en forma estándar.

Cuando los coeficientes son grandes, a veces es menos trabajo usar la fórmula cuadrática en lugar de tratar de faccionarla. En este caso, a=1, b=1 y c=−240. Sustituir en la fórmula cuadrática y luego simplificar.

$\begin{array}{ll}{n=\frac{-1-31}{2}} & {n=\frac{-1+31}{2}} \\ {n=\frac{-32}{2}} & {n=\frac{30}{2}} \\ {n=-16} & {n=15}\end{array}$

Dado que el problema requiere números enteros positivos, desprecie la solución negativa y elija n = 15.

$\begin{aligned} n+1 &=\color{OliveGreen}{15}\color{black}{+}1 \\ &=16 \end{aligned}$

Respuesta:

Los enteros positivos son 15 y 16.

Claves para llevar

Determinar el número y tipo de soluciones a cualquier ecuación cuadrática en forma estándar utilizando el discriminante,$b^{2}−4ac$. Si el discriminante es negativo, entonces las soluciones no son reales. Si el discriminante es positivo, entonces las soluciones son reales. Si el discriminante es 0, entonces sólo hay una solución, una doble raíz.
Elija el método adecuado para resolver una ecuación cuadrática en función del valor de su discriminante. Si bien la fórmula cuadrática resolverá cualquier ecuación cuadrática, puede que no sea el método más eficiente.
Al resolver aplicaciones, use las palabras y frases clave para establecer una ecuación algebraica que modele el problema. En esta sección, la configuración suele implicar una ecuación cuadrática.

Ejercicio$\PageIndex{3}$ use the discriminant

Calcular el discriminante y utilizarlo para determinar el número y tipo de soluciones. No resuelva.

$x^{2}+2x+3=0$
$x^{2}−2x−3=0$
$3x^{2}−1x−2=0$
$3x^{2}−1x+2=0$
$9y^{2}+2=0$
$9y^{2}−2=0$
$5x^{2}+x=0$
$5x^{2}−x=0$
$12x^{2}−2x+52=0$
$12x^{2}−x−12=0$
$−x^{2}−2x+4=0$
$−x^{2}−4x+2=0$
$4t^{2}−20t+25=0$
$9t^{2}−6t+1=0$

Contestar

1. −8, ninguna solución real

3. 25, dos soluciones reales

5. −72, ninguna solución real

7. 1, dos soluciones reales

9. −1, ninguna solución real

11. 20, dos soluciones reales

13. 0, una solución real

Ejercicio$\PageIndex{4}$ solving

Elija el método adecuado para resolver lo siguiente.

$x^{2}−2x−3=0$
$x^{2}+2x+3=0$
$3x^{2}−x−2=0$
$3x^{2}−x+2=0$
$9y^{2}+2=0$
$9y^{2}−2=0$
$5x^{2}+x=0$
$5x^{2}−x=0$
$12x^{2}−2x+52=0$
$12x^{2}−x−12=0$
$−x^{2}−2x+4=0$
$−x^{2}−4x+2=0$
$4t^{2}−20t+25=0$
$9t^{2}−6t+1=0$
$y^{2}−4y−1=0$
$y^{2}−6y−3=0$
$25x^{2}+1=0$
$36x^{2}+4=0$
$5t^{2}−4=0$
$2t^{2}−9=0$
$12x^{2}−94x+1=0$
$3x^{2}+12x−16=0$
$36y^{2}=2y$
$50y^{2}=−10y$
$x(x−6)=−29$
$x(x−4)=−16$
$4y(y+1)=5$
$2y(y+2)=3$
$-3x^{2}=2x+1$
$3x^{2}+4x=−2$
$6(x+1)2=11x+7$
$2(x+2)2=7x+11$
$9t^{2}=4(3t−1)$
$5t(5t−6)=−9$
$(x+1)(x+7)=3$
$(x−5)(x+7)=14$

Contestar

1. $-1, 3$

3. $-\frac{2}{3} , 1$

5. No hay solución real

7. $-\frac{1}{5} , 0$

9. No hay solución real

11. $-1\pm\sqrt{5}$

13. $\frac{5}{2}$

15. $2\pm\sqrt{5}$

17. No hay solución real

19. $\pm\frac{2 \sqrt{5}}{5}$

21. $\frac{1}{2}, 4$

23. $0, \frac{1}{18}$

25. No hay solución real

27. $\frac{-1\pm\sqrt{6}}{2}$

29. No hay solución real

31. $-\frac{1}{2}, \frac{1}{3}$

33. $\frac{2}{3}$

35. $-4\pm 2\sqrt{3}$

Ejercicio$\PageIndex{5}$ applications number problems

Configura una ecuación algebraica y úsala para resolver lo siguiente.

Un número real positivo es 2 menos que otro. Cuando se agrega 4 veces más grande al cuadrado del menor, el resultado es 49. Encuentra los números.
Un número real positivo es 1 más que otro. Cuando el doble de menor se resta del cuadrado del mayor, el resultado es 4. Encuentra los números.
Un número real positivo es 6 menos que otro. Si la suma de los cuadrados de los dos números es 38, entonces encuentra los números.
Un número real positivo es 1 más que dos veces otro. Si se resta 4 veces el número menor del cuadrado del mayor, entonces el resultado es 21. Encuentra los números.

Contestar

1. $3\sqrt{5}$y\ (3\ sqrt {5} -2)

3. $\sqrt{10\pm 3$

Ejercicio$\PageIndex{6}$ applications geometry problems

Redondea tus respuestas a la centésima más cercana.

El área de un rectángulo es de 60 pulgadas cuadradas. Si la longitud es 3 veces la anchura, entonces encuentra las dimensiones del rectángulo.
El área de un rectángulo es de 6 pies cuadrados. Si el largo es 2 pies más que el ancho, entonces encuentra las dimensiones del rectángulo.
El área de un rectángulo es de 27 metros cuadrados. Si la longitud es de 6 metros menos de 3 veces el ancho, entonces encuentra las dimensiones del rectángulo.
El área de un triángulo es de 48 pulgadas cuadradas. Si la base es 2 veces la altura, entonces encuentra la longitud de la base.
El área de un triángulo es de 14 pies cuadrados. Si la base mide 4 pies más de 2 veces la altura, entonces encuentra la longitud de la base y la altura.
El área de un triángulo es de 8 metros cuadrados. Si la base es 4 metros menos que la altura, entonces encuentra la longitud de la base y la altura.
El perímetro de un rectángulo es de 54 centímetros y el área es de 180 centímetros cuadrados. Encuentra las dimensiones del rectángulo.
El perímetro de un rectángulo es de 50 pulgadas y el área es de 126 pulgadas cuadradas. Encuentra las dimensiones del rectángulo.
George mantiene un exitoso jardín de 6 metros por 8 metros. La próxima temporada planea duplicar el área de siembra aumentando el ancho y la altura en una cantidad igual. ¿En cuánto debe aumentar la longitud y la anchura?
Se construirá un borde de ladrillo uniforme alrededor de un jardín de 6 pies por 8 pies. Si el área total del jardín, incluyendo el borde, va a ser de 100 pies cuadrados, entonces encuentre el ancho del borde de ladrillo.

Contestar

1. Largo: 13.42 pulgadas; ancho: 4.47 pulgadas

3. Largo: 6.48 metros; ancho: 4.16 metros

5. Altura: 2.87 pies; base: 9.74 pies

7. Largo: 15 centímetros; ancho: 12 centímetros

9. 2.85 metros

Ejercicio$\PageIndex{7}$ applications pythagorean theorem

Si los lados de un cuadrado miden$\sqrt{106}$ unidades, entonces encuentra la longitud de la diagonal.
Si la diagonal de un cuadrado mide$\sqrt{310}$ unidades, entonces encuentra la longitud de cada lado.
La diagonal de un rectángulo mide$\sqrt{63}$ pulgadas. Si el ancho es de 4 pulgadas menos que el largo, entonces encuentra las dimensiones del rectángulo.
La diagonal de un rectángulo mide$\sqrt{23}$ pulgadas. Si el ancho es de 2 pulgadas menos que el largo, entonces encuentra las dimensiones del rectángulo.
La parte superior de una escalera de 20 pies, apoyada contra un edificio, alcanza una altura de 18 pies. ¿A qué distancia está la base de la escalera de la pared? Redondea a la centésima más cercana.
Para usar una escalera de manera segura, la base debe colocarse aproximadamente 1/4 de la longitud de la escalera lejos de la pared. Si una escalera de 20 pies se va a usar de manera segura, entonces ¿qué tan alto contra un edificio alcanzará la parte superior de la escalera? Redondea a la centésima más cercana.
La diagonal de un monitor de televisión mide 32 pulgadas. Si el monitor tiene una relación de aspecto 3:2, entonces determine su longitud y ancho. Redondea a la centésima más cercana.
La diagonal de un monitor de televisión mide 52 pulgadas. Si el monitor tiene una relación de aspecto 16:9, entonces determine su longitud y ancho. Redondea a la centésima más cercana.

Contestar

1. $\sqrt{203}$unidades

3. Largo:$2+\sqrt{52}$ pulgadas; ancho:$−2+\sqrt{52}$ pulgadas

5. $2\sqrt{19} \approx 8.72$pies

7. Largo: 26.63 pulgadas; ancho: 17.75 pulgadas

Ejercicio$\PageIndex{8}$ applications business problems

La ganancia en dólares de ejecutar una línea de montaje que produce uniformes personalizados cada día viene dada por la función$P(t)=−40t^{2}+960t−4,000$, donde t representa el número de horas que la línea está en operación.
1. Calcular la ganancia al ejecutar la línea de montaje durante 10 horas diarias.
2. Calcule el número de horas que debe funcionar la línea de montaje para poder pararse. Redondear a la décima de hora más cercana.
El beneficio en dólares generado por la producción y venta de x lámparas personalizadas viene dado por la función$P(x)=−10x^{2}+800x−12,000$.
1. Calcular el beneficio sobre la producción y venta de 35 lámparas.
2. Calcular el número de lámparas que se deben vender para obtener ganancias $3,000.
Si se invierten $1,200 en una cuenta que gana una tasa de interés anual r, entonces la cantidad A que está en la cuenta al final de 2 años viene dada por la fórmula$A=1,200(1+r)^{2}$. Si al término de 2 años el monto en la cuenta es de $1,335.63, entonces ¿cuál era la tasa de interés?
Una empresa manufacturera ha determinado que el ingreso diario, R, en miles de dólares depende del número, n, de paletas de producto vendido de acuerdo a la fórmula$R=12n−0.6n^{2}$. Determinar el número de paletas que deben venderse para mantener los ingresos en $60,000 diarios.

Contestar

1. a. $1,600; b. 5.4 horas y 18.6 horas

3. 5.5%

Ejercicio$\PageIndex{9}$ applications projectile problems

La altura de un proyectil lanzado hacia arriba a una velocidad de 32 pies/segundo desde una altura de 128 pies viene dada por la función$h(t)=−16t^{2}+32t+128$.
1. ¿Cuál es la altura del proyectil a 1/2 segundo?
2. ¿A qué hora después del lanzamiento alcanzará el proyectil una altura de 128 pies?
La altura de un proyectil lanzado hacia arriba a una velocidad de 16 pies/segundo desde una altura de 192 pies viene dada por la función$h(t)=−16t^{2}+16t+192$.
1. ¿Cuál es la altura del proyectil a 3/2 segundos?
2. ¿A qué hora llegará el proyectil a 128 pies?
La altura de un objeto caído desde la parte superior de un edificio de 144 pies viene dada por$h(t)=−16t^{2}+144$. ¿Cuánto tiempo tardará en llegar a un punto a medio camino del suelo?
La altura de un proyectil disparado hacia arriba en el aire a 80 pies/segundo desde el suelo viene dada por$h(t)=−16t^{2}+80t$. ¿A qué hora llegará el proyectil a 95 pies?

Contestar

1. a. 140 pies; b. 0 segundos y 2 segundos

3. 2.12 segundos

Ejercicio$\PageIndex{10}$ applications discussion board

Discutir la estrategia de usar siempre la fórmula cuadrática para resolver ecuaciones cuadráticas.
Enumere todos los métodos que hemos aprendido hasta ahora para resolver ecuaciones cuadráticas. Discuta los pros y los contras de cada uno.

Contestar: 1. Las respuestas pueden variar

Discriminante positivo:	\(b^{2}-4ac >0\)	Dos soluciones reales
Cero discriminante:	\(b^{2}-4ac =0\)	Una solución real
Discriminante negativo:	\(b^{2}-4ac <0\)	No hay solución real