9.5: Graficar Parábolas

Última actualización
Guardar como PDF

Page ID: 110138

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Grafica una parábola.
Encuentra las intercepciones y el vértice de una parábola.
Encuentra el vértice de una parábola completando el cuadrado.

La Gráfica de una Ecuación Cuadrática

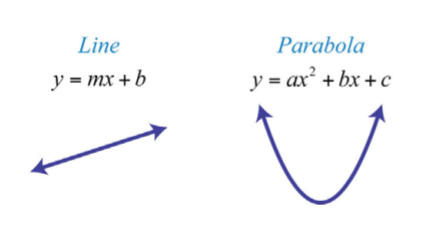
Sabemos que cualquier ecuación lineal con dos variables se puede escribir en la forma$y=mx+b$ y que su gráfica es una línea. En esta sección, veremos que cualquier ecuación cuadrática de la forma$y=ax^{2}+bx+c$ tiene una gráfica curva llamada parábola.

Captura de pantalla (234) .png — Figura$\PageIndex{1}$

Dos puntos determinan cualquier línea. No obstante, como una parábola es curva, deberíamos encontrar más de dos puntos. En este texto, determinaremos al menos cinco puntos como medio para producir un boceto aceptable. Para comenzar, graficamos nuestra primera parábola trazando puntos. Dada una ecuación cuadrática de la forma$y=ax^{2}+bx+c$, x es la variable independiente e y es la variable dependiente. Elija algunos valores para x y luego determine los valores y correspondientes. Después, trazar los puntos y bosquejar la gráfica.

Ejemplo$\PageIndex{1}$

Gráfica por puntos de trazado:

$y=x^{2}-2x-3$

Solución:

En este ejemplo, elija los valores x {−2, −1, 0, 1, 2, 3, 4} y calcule los valores y correspondientes.

Captura de pantalla (235) .png — Figura$\PageIndex{2}$

Trazar estos puntos y determinar la forma de la gráfica.

Respuesta:

Captura de pantalla (237) .png — Figura$\PageIndex{3}$

Al graficar, queremos incluir ciertos puntos especiales en la gráfica. La intersección y es el punto donde la gráfica se cruza con el eje y. Las intercepciones x son los puntos donde la gráfica se cruza con el eje x. El vértice es el punto que define el mínimo o máximo de la gráfica. Por último, la línea de simetría (también llamada eje de simetría) es la línea vertical a través del vértice, alrededor de la cual la parábola es simétrica.

Captura de pantalla (238) .png — Figura$\PageIndex{4}$

Para cualquier parábola, encontraremos el vértice y -intercepción. Además, si existen las intercepciones x, entonces también vamos a querer determinarlas. Adivinar los valores x de estos puntos especiales no es práctico; por lo tanto, desarrollaremos técnicas que faciliten encontrarlos. Muchas de estas técnicas serán utilizadas ampliamente a medida que avancemos en nuestro estudio del álgebra. Dada una ecuación cuadrática de la forma$y=ax^{2}+bx+c$, encuentra la intersección y estableciendo x=0 y resolviendo. En general$y=a(0)^{2}+b(0)+c=c$,, y tenemos

\ (\ color {cerúleo} {y-intercept}

\ [(0, c]\)

A continuación, recordemos que las intercepciones x, si existen, se pueden encontrar estableciendo y=0. Haciendo esto, tenemos$0=a^{2}+bx+c$, que tiene soluciones generales dadas por la fórmula cuadrática,$x=\frac{−b±\sqrt{b^{2}−4ac}}{2a}$. Por lo tanto, las intercepciones x tienen esta forma general:

$\color{Cerulean}{x-intercepts}$

Usando el hecho de que una parábola es simétrica, podemos determinar la línea vertical de simetría usando las intercepciones x. Para ello, encontramos el valor x a medio camino entre las intercepciones x tomando un promedio de la siguiente manera:

Por lo tanto, la línea de simetría es la línea vertical:

$\color{Cerulean}{Line\:of\:symmetry}$

\[x=-\frac{b}{2 a}\]

Podemos usar la línea de simetría para encontrar el valor x del vértice. Los pasos para graficar una parábola se describen en el siguiente ejemplo.

Ejemplo$\PageIndex{2}$

Gráfica:

Solución

Paso 1: Determinar la intercepción y. Para ello, establezca x = 0 y resuelva para y.

La intercepción y es (0, 3).

Paso 2: Determinar las intercepciones x. Para ello, establece y = 0 y resuelve para x.

$\begin{array}{rlr}{x+3} & {=0} & {\text { or }} & {x-1=0} \\ {x} & {=-3} & {} & {x=1}\end{array}$

Aquí cuando y = 0, obtenemos dos soluciones. Hay dos intercepciones x, (−3, 0) y (1, 0).

Paso 3: Determinar el vértice. Una forma de hacerlo es usar la ecuación para la línea de simetría$x=\frac{-b}{2 a}$,, para encontrar el valor x del vértice. En este ejemplo, a = −1 y b = −2:

Sustituye −1 en la ecuación original para encontrar el valor y correspondiente.

El vértice es (−1, 4).

Paso 4: Determinar puntos extra para que tengamos al menos cinco puntos para trazar. En este ejemplo, bastará otro punto. Elija x = −2 y encuentre el valor y correspondiente.

Captura de pantalla (239) .png — Figura$\PageIndex{5}$

Nuestro quinto punto es (-2,3).

Paso 5: Trazar los puntos y bosquejar la gráfica. Para recapitular, los puntos que hemos encontrado son

Mesa$\PageIndex{1}$
Intercepción en Y:	(0,3)
X-intercepción:	(-3,0) y (1,0)
Vértice:	(-1,4)
Punto extra:	(-2,3)

Respuesta:

Captura de pantalla (240) .png — Figura$\PageIndex{6}$

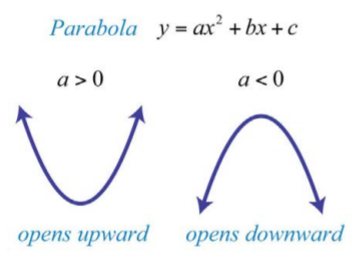
La parábola se abre hacia abajo. En general, utilice el coeficiente principal para determinar si la parábola se abre hacia arriba o hacia abajo. Si el coeficiente inicial es negativo, como en el ejemplo anterior, entonces la parábola se abre hacia abajo. Si el coeficiente principal es positivo, entonces la parábola se abre hacia arriba.

Captura de pantalla (241) .png — Figura$\PageIndex{7}$

Todas las ecuaciones cuadráticas de la forma$y=ax^{2}+bx+c$ tienen gráficas parabólicas con intercepción y (0, c). Sin embargo, no todas las parábolas tienen x intercepciones.

Ejemplo$\PageIndex{3}$

Gráfica:

$y=2x^{2}+4x+5$

Solución:

Debido a que el coeficiente principal 2 es positivo, tenga en cuenta que la parábola se abre hacia arriba. Aquí c = 5 y la intersección y es (0, 5). Para encontrar las intercepciones x, establezca y = 0.

$\begin{array}{l}{y=2 x^{2}+4 x+5} \\ {0=2 x^{2}+4 x+5}\end{array}$

En este caso, a = 2, b = 4 y c = 5. Utilizar el discriminante para determinar el número y tipo de soluciones.

Dado que el discriminante es negativo, concluimos que no hay soluciones reales. Debido a que no hay soluciones reales, no hay intercepciones x. A continuación, determinamos el valor x del vértice.

Dado que el valor x del vértice es −1, sustituya en la ecuación original para encontrar el valor y correspondiente.

$\begin{aligned} y &=2 x^{2}+4 x+5 \\ &=2(\color{OliveGreen}{-1}\color{black}{)}^{2}+4(\color{OliveGreen}{-1}\color{black}{)}+5 \\ &=2-4+5 \\ &=3 \end{aligned}$

El vértice es (−1, 3). Hasta el momento, sólo tenemos dos puntos. Para determinar tres más, elija algunos valores x a cada lado de la línea de simetría, x = −1. Aquí elegimos x -valores −3, −2 y 1.

Captura de pantalla (242) .png — Figura$\PageIndex{8}$

Para resumir, tenemos

Mesa$\PageIndex{2}$
Intercepción en Y:	(0,5)
X-intercepta:	Ninguno
Vértice:	(-1,3)
Puntos extra	(-3,11), (-2,5), (1,11)

Trazar los puntos y bosquejar la gráfica.

Respuesta:

Captura de pantalla (243) .png — Figura$\PageIndex{9}$

Ejemplo$\PageIndex{4}$

Gráfica:

Solución

Tenga en cuenta que a = −2: la parábola se abre hacia abajo. Dado que c = −18, la intersección y es (0, −18). Para encontrar las intercepciones x, establezca y = 0.

Resolver factorizando.

$\begin{array}{rrr}{x-3=0} & {\text { or }} & {x-3=0} \\ {x=3} && {x=3}\end{array}$

Aquí x = 3 es una raíz doble, por lo que sólo hay una x -intercepción, (3, 0). De la ecuación original, a = −2, b = 12 y c = −18. El valor x del vértice se puede calcular de la siguiente manera:

$\begin{aligned} x &=\frac{-b}{2 a} \\ &=\frac{-(\color{OliveGreen}{12}\color{black}{)}}{2(\color{OliveGreen}{-2}\color{black}{)}} \\ &=\frac{-12}{-4} \\ &=3 \end{aligned}$

Dado que el valor x del vértice es 3, sustituya en la ecuación original para encontrar el valor y correspondiente.

Por lo tanto, el vértice es (3, 0), que pasa a ser el mismo punto que la intersección x. Hasta el momento, sólo tenemos dos puntos. Para determinar tres más, elija algunos valores x a cada lado de la línea de simetría, x = 3 en este caso.

Elija los valores x 1, 5 y 6.

Captura de pantalla (245) .png — Figura$\PageIndex{10}$

Mesa\(\PageIndex{3}\)
Intercepción en Y:	(0, -18)
X-intercepta:	(3, 0)
Vértice:	(3, 0)
Puntos extra:	(1, -8), (5, -8), (6, -18)

Ejemplo$\PageIndex{5}$

Gráfica:

Solución:

Desde a = 1, la parábola se abre hacia arriba. Además, c = −1, por lo que la intersección y es (0, −1). Para encontrar las intercepciones x, establezca y = 0.

En este caso, resuelve usando la fórmula cuadrática con a = 1, b = −2 y c = −1.

Aquí obtenemos dos soluciones reales para x, y así hay dos intercepciones x:

$(1-\sqrt{2}, 0) \quad \text { and } \qquad(1+\sqrt{2}, 0)$

Valores aproximados usando una calculadora:

$(-0.41,0) \qquad \text { and } \qquad(2.41,0)$

Usa las respuestas aproximadas para colocar el par ordenado en la gráfica.

No obstante, presentaremos las x -intercepciones exactas en la gráfica. A continuación, encuentra el vértice.

$\begin{aligned} x &=\frac{-b}{2 a} \\ &=\frac{-(\color{OliveGreen}{-2}\color{black}{)}}{2(\color{OliveGreen}{1}\color{black}{)}} \\ &=\frac{2}{2} \\ &=1 \end{aligned}$

Dado que el valor x del vértice es 1, sustituya en la ecuación original para encontrar el valor y correspondiente.

El vértice es (1, -2). Necesitamos un punto más.

Captura de pantalla (247) .png — Figura$\PageIndex{12}$

Mesa\(\PageIndex{4}\)
Intercepción en Y:	(0, -1)
X-intercepta:	\((1-\sqrt{2}, 0)\)y\((1+\sqrt{2}, 0)\)
Vértice:	\((1, -2)\)
Punto extra:	\((2, -1)\)

Ejercicio$\PageIndex{1}$

Gráfica:

$y=9x^{2}-5$

Contestar: $Captura de pantalla (248) .png$
Figura$\PageIndex{14}$

Encontrar el Máximo y el Mínimo

A menudo es útil encontrar los valores máximos y/o mínimos de funciones que modelan aplicaciones de la vida real. Para encontrar estos valores importantes dados una función cuadrática, usamos el vértice. Si el coeficiente principal a es positivo, entonces la parábola se abre hacia arriba y habrá un valor mínimo y. Si el coeficiente principal a es negativo, entonces la parábola se abre hacia abajo y habrá un valor y máximo.

Ejemplo$\PageIndex{6}$

Determinar el máximo o mínimo:

$y=−4x^{2}+24x−35$

Solución:

Desde a = −4, sabemos que la parábola se abre hacia abajo y habrá un valor y máximo. Para encontrarlo, primero encontramos el valor x del vértice.

$\begin{aligned} x &=-\frac{b}{2 a} \qquad\quad\color{Cerulean}{x-value\:of\:the\:vertex.} \\ &=-\frac{24}{2(-4)}\quad\:\color{Cerulean}{Substitute\:a=-4\:and\:b=24.} \\ &=-\frac{24}{-8} \qquad\:\: \color{Cerulean}{Simplify.} \\ &=3 \end{aligned}$

El valor x del vértice es 3. Sustituya este valor en la ecuación original para encontrar el valor y correspondiente.

El vértice es (3, 1). Por lo tanto, el valor y máximo es 1, que ocurre cuando x = 3, como se ilustra a continuación:

Figura$\PageIndex{15}$

Nota

No se requiere la gráfica para responder a esta pregunta.

Respuesta:

El máximo es 1.

Ejemplo$\PageIndex{7}$

Determinar el máximo o mínimo:

$y=4x^{2}−32x+62$

Solución:

Desde a = +4, la parábola se abre hacia arriba y hay un valor mínimo y. Comience por encontrar el valor x del vértice.

$\begin{aligned} x &=-\frac{b}{2 a} \\ &=-\color{black}{\frac{\color{OliveGreen}{-32}}{\color{black}{2}(\color{OliveGreen}{4}\color{black}{)}}}\qquad\color{Cerulean}{Substitute\:a=4\:and\:b=-32.} \\ &=-\frac{-32}{8}\qquad\color{Cerulean}{Simplify.} \\ &=4 \end{aligned}$

Sustituye x = 4 en la ecuación original para encontrar el valor y correspondiente.

El vértice es (4, −2). Por lo tanto, el valor mínimo y de −2 ocurre cuando x = 4, como se ilustra a continuación:

Figura$\PageIndex{16}$

Respuesta:

El mínimo es -2.

Ejercicio$\PageIndex{2}$

Determinar el máximo o mínimo:

$y=(x-3)^{2}-9$

Contestar: El mínimo es −9.

Una parábola, que se abre hacia arriba o hacia abajo (a diferencia de los lados), define una función y se extiende indefinidamente hacia la derecha y hacia la izquierda como indican las flechas. Por lo tanto, el dominio (el conjunto de valores x) consiste en todos los números reales. Sin embargo, el rango (el conjunto de valores y) está limitado por el valor y del vértice.

Ejemplo$\PageIndex{8}$

Determine el dominio y el rango:

$y=x^{2}-4x+3$

Solución:

Primero, tenga en cuenta que dado que a=1 es positivo, la parábola se abre hacia arriba. De ahí que habrá un valor mínimo y. Para encontrar ese valor, busque el valor x del vértice:

$x=-\frac{b}{2 a}=-\frac{-4}{2(1)}=2$

Después sustituya en la ecuación para encontrar el valor y correspondiente.

El vértice es (2, −1). El rango consiste en el conjunto de valores y mayores o iguales que el valor mínimo y −1.

Figura$\PageIndex{17}$

Respuesta:

Dominio: R =$(-\infty, \infty)$; Rango:$[-1, \infty)$

Ejemplo$\PageIndex{9}$

La altura en pies de un proyectil viene dada por la función$h(t)=−16t^{2}+72t$, donde t representa el tiempo en segundos después del lanzamiento. ¿Cuál es la altura máxima que alcanza el proyectil?

Solución:

Aquí a=−16, y la parábola se abre hacia abajo. Por lo tanto, el valor y del vértice determina la altura máxima. Comience por encontrar el valor x del vértice:

$x=-\frac{b}{2 a}=-\frac{72}{2(-16)}=\frac{72}{32}=\frac{9}{4}$

La altura máxima ocurrirá en 9/4 = 2¼ segundos. Sustituya este tiempo en la función para determinar la altura alcanzada.

$\begin{aligned} h\left(\frac{9}{4}\right) &=-16\left(\frac{9}{4}\right)^{2}+72\left(\frac{9}{4}\right) \\ &=-16\left(\frac{81}{16}\right)+72\left(\frac{9}{4}\right) \\ &=-81+162 \\ &=81 \end{aligned}$

Respuesta:

La altura máxima del proyectil es de 81 pies.

Encontrar el vértice completando el cuadrado

En esta sección, demostramos un enfoque alternativo para encontrar el vértice. Cualquier ecuación cuadrática se$y=ax^{2}+bx+c$ puede reescribir en la forma

\[y=a(x-h)^{2}+k\]

En esta forma, el vértice es (h, k).

Ejemplo$\PageIndex{10}$

Determine el vértice:

$y=-4(x-3)^{2}+1$

Solución:

Cuando la ecuación está en esta forma, podemos leer el vértice directamente de la ecuación.

$\begin{array}{l}{y=\:a\:(\:x-h)^{2}+k} \\ \color{Cerulean}{\qquad\qquad\quad\downarrow\quad\:\:\downarrow} \\ {y=-4(x-3)^{2}+1}\end{array}$

Aquí h =3 y k =1.

Respuesta:

El vértice es (3, 1).

Ejemplo$\PageIndex{11}$

Determine el vértice:

$y=2(x+3)^{2}-2$

Solución:

Reescribe la ecuación de la siguiente manera antes de determinar h y k.

$\begin{array}{l}{y=\:a\:(\:x\:-h)^{2}\:\:\:\:+\:\:\:k} \\ \color{Cerulean}{\qquad\qquad\quad\:\downarrow\qquad\quad\downarrow} \\ {y=2(x-(-3))^{2}+(-2)}\end{array}$

Aquí h =-3 y k =-2.

Respuesta:

El vértice es (-3, -2).

A menudo la ecuación no se da en esta forma. Para obtener este formulario, complete el cuadrado.

Ejemplo$\PageIndex{12}$

Reescribir en$y=a(x−h)^{2}+k$ forma y determinar el vértice:$y=x^{2}+4x+9$.

Solución:

Comience por dejar espacio para el término constante que completa la plaza.

$\begin{aligned} y &=x^{2}+4 x+9 \\ &=x^{2}+4 x+\underline\quad+9-\underline\quad\end{aligned}$

La idea es sumar y restar el valor que completa el cuadrado,$\frac{b^{2}}{2}$, y luego factorial. En este caso, sumar y restar$\frac{4^{2}}{2} = 2^{2} = 4$.

$\begin{aligned} y &=x^{2}+4 x+9 \qquad\quad\:\:\:\color{Cerulean}{Add\:and\:subtract\:4.} \\ &=\underbrace{x^{2}+4 x\color{Cerulean}{+4}}_{\text { factor }}+9\color{Cerulean}{-4} \quad\color{Cerulean}{Factor.} \\ &=(x+2)(x+2)+5 \\ &=(x+2)^{2}+5 \end{aligned}$

Sumar y restar el mismo valor dentro de una expresión no lo cambia. Hacerlo equivale a sumar 0. Una vez que la ecuación está en esta forma, podemos determinar fácilmente el vértice.

$\begin{array}{c}{y=a(x-h)^{2}\:+\:\:k} \\ \color{Cerulean}{\qquad\quad\quad\:\:\downarrow\qquad\downarrow} \\ {y=(x-(-2))^{2}+5}\end{array}$

Aquí h =-2 y k =5.

Respuesta:

El vértice es (-2, 5).

Si hay un coeficiente principal distinto de 1, entonces primero debemos factorial el coeficiente principal de los dos primeros términos del trinomio.

Ejemplo$\PageIndex{13}$

Reescribir en$y=a(x−h)^{2}+k$ forma y determinar el vértice:$y=2x^{2}−4x+8$.

Solución:

Desde a = 2, factifique esto de los dos primeros términos para completar el cuadrado. Deja espacio dentro de los paréntesis para agregar un término constante.

Ahora usa −2 para determinar el valor que completa el cuadrado. En este caso,$\frac{(-2)^{2}}{2}=\((-1)^{2}=1$. Sumar y restar 1 y factificar de la siguiente manera:

De esta forma, podemos determinar fácilmente el vértice.

$\begin{array}{l}{y=a(x-h)^{2}+k} \\ \color{Cerulean}{\qquad\qquad\:\downarrow\quad\:\:\:\downarrow}\\ {y=2(x-1)^{2} \:+6}\end{array}$

Aquí h =1 y k =6.

Respuesta:

El vértice es (1, 6).

Ejercicio$\PageIndex{3}$

Reescribe en$y=a(x-h)^{2}+k$ forma y determina el vértice:

$y=-2x^{2}-12x+3$.

Contestar: $y=-2(x+3)^{2}+21$; vértice:$(-3, 21)$

Claves para llevar

La gráfica de cualquier ecuación cuadrática$y=ax^{2}+bx+c$, donde a, b y c son números reales y a≠ 0, se llama parábola.
Al graficar parábolas, encuentra el vértice y la intercepción y. Si existen las intercepciones x, búsquelas también. Además, asegúrese de encontrar soluciones de pares ordenados a ambos lados de la línea de simetría,$x=\frac{-b^{2}}{a}$.
Utilice el coeficiente inicial, a, para determinar si una parábola se abre hacia arriba o hacia abajo. Si a es positivo, entonces se abre hacia arriba. Si a es negativo, entonces se abre hacia abajo.
El vértice de cualquier parábola tiene un valor x igual a$x=\frac{-b^{2}}{a}$. Después de encontrar el valor x del vértice, sumételo en la ecuación original para encontrar el valor y correspondiente. Este valor y es un máximo si la parábola se abre hacia abajo, y es un mínimo si la parábola se abre hacia arriba.
El dominio de una parábola que se abre hacia arriba o hacia abajo consiste en todos los números reales. El rango está limitado por el valor y del vértice.
Un enfoque alternativo para encontrar el vértice es reescribir la ecuación cuadrática en la forma$y=a(x−h)^{2}+k$. Cuando está en esta forma, el vértice es (h, k) y se puede leer directamente de la ecuación. Para obtener esta forma, toma$y=ax^{2}+bx+c$ y completa la plaza.

Ejercicio$\PageIndex{4}$ the graph of quadratic equations

¿La parábola se abre hacia arriba o hacia abajo? Explique.

$y=x^{2}−9x+20$
$y=x^{2}−12x+32$
$y=−2x^{2}+5x+12$
$y=−6x^{2}+13x−6$
$y=64−x^{2}$
$y=−3x+9x^{2}$

Contestar

1. Al alza

3. A la baja

5. A la baja

Ejercicio$\PageIndex{5}$ the graph of quadratic equations

Determinar las intercepciones x e y.

$y=x^{2}+4x−12$
$y=x^{2}−13x+12$
$y=2x^{2}+5x−3$
$y=3x^{2}−4x−4$
$y=−5x^{2}−3x+2$
$y=−6x^{2}+11x−4$
$y=4x^{2}−25$
$y=9x^{2}−49$
$y=x^{2}−x+1$
$y=5x^{2}+15x$

Contestar

1. x -intercepta:$(−6, 0), (2, 0)$; y -interceptar:$(0, −12)$

3. x -intercepta:$(−3, 0), (\frac{1}{2}, 0)$; y -interceptar:$(0, −3)$

5. x -intercepta:$(−1, 0), (\frac{2}{5}, 0)$; y -interceptar:$(0, 2)$

7. x -intercepta:$(−\frac{5}{2}, 0), (\frac{5}{2}, 0)$; y -interceptar:$(0, −25)$

9. x -intercepta: ninguno; y -interceptar:$(0, 1)$

Ejercicio$\PageIndex{6}$ the graph of quadratic equations

Encuentra el vértice y la línea de simetría.

$y=−x^{2}+10x−34$
$y=−x^{2}−6x+1$
$y=−4x^{2}+12x−7$
$y=−9x^{2}+6x+2$
$y=4x^{2}−1$
$y=x^{2}−16$

Contestar

1. Vértice:$(5, −9)$; línea de simetría:$x=5$

3. Vértice:$(\frac{3}{2}, 2)$; línea de simetría:$x= \frac{3}{2}$

5. Vértice:$(0, −1)$; línea de simetría:$x=0$

Ejercicio$\PageIndex{7}$ the graph of quadratic equations

Gráfica. Encuentra el vértice y la intercepción y. Además, encuentra las x -intercepciones si existen.

$y=x^{2}−2x−8$
$y=x^{2}−4x−5$
$y=−x^{2}+4x+12$
$y=−x^{2}−2x+15$
$y=x^{2}−10x$
$y=x^{2}+8x$
$y=x^{2}−9$
$y=x^{2}−25$
$y=1−x^{2}$
$y=4−x^{2}$
$y=x^{2}−2x+1$
$y=x^{2}+4x+4$
$y=−4x^{2}+12x−9$
$y=−4x^{2}−4x+3$
$y=x^{2}−2$
$y=x^{2}−3$
$y=−4x^{2}+4x−3$
$y=4x^{2}+4x+3$
$y=x^{2}−2x−2$
$y=x^{2}−6x+6$
$y=−2x^{2}+6x−3$
$y=−4x^{2}+4x+1$
$y=x^{2}+3x+4$
$y=−x^{2}+3x−4$
$y=−2x^{2}+3$
$y=−2x^{2}−1$
$y=2x^{2}+4x−3$
$y=3x^{2}+2x−2$

Contestar

Captura de pantalla (253) .png — Figura$\PageIndex{18}$

Captura de pantalla (254) .png — Figura$\PageIndex{19}$

Captura de pantalla (256) .png — Figura$\PageIndex{20}$

Captura de pantalla (257) .png — Figura$\PageIndex{21}$

Captura de pantalla (258) .png — Figura$\PageIndex{22}$

11.

Captura de pantalla (259) .png — Figura$\PageIndex{23}$

13.

Captura de pantalla (260) .png — Figura$\PageIndex{24}$

15.

Captura de pantalla (261) .png — Figura$\PageIndex{25}$

17.

Captura de pantalla (262) .png — Figura$\PageIndex{26}$

19.

Captura de pantalla (263) .png — Figura$\PageIndex{27}$

21.

Captura de pantalla (264) .png — Figura$\PageIndex{28}$

23.

Captura de pantalla (265) .png — Figura$\PageIndex{29}$

25.

Captura de pantalla (266) .png — Figura$\PageIndex{30}$

27.

Captura de pantalla (267) .png — Figura$\PageIndex{31}$

Ejercicio$\PageIndex{8}$ maximum or minimum

Determinar el valor y máximo o mínimo.

$y=−x^{2}−6x+1$
$y=−x^{2}−4x+8$
$y=25x^{2}−10x+5$
$y=16x^{2}−24x+7$
\ (y=−x^ {2}
$y=1−9x^{2}$
$y=20x−10x^{2}$
$y=12x+4x^{2}$
$y=3x^{2}−4x−2$
$y=6x^{2}−8x+5$

Contestar

1. Máximo:$y = 10$

3. Mínimo:$y = 4$

5. Máximo:$y = 0$

7. Máximo:$y = 10$

9. Mínimo:$y = −\frac{10}{3}$

Ejercicio$\PageIndex{9}$ maximum or minimum

Dadas las siguientes funciones cuadráticas, determinar el dominio y el rango.

$f(x)=3x^{2}+30x+50$
$f(x)=5x^{2}−10x+1$
$g(x)=−2x^{2}+4x+1$
$g(x)=−7x^{2}−14x−9$
La altura en pies que alcanza un beisbol arrojado hacia arriba a una velocidad de 48 pies/segundo desde el suelo viene dada por la función$h(t)=−16t^{2}+48t$, donde t representa el tiempo en segundos. ¿Cuál es la altura máxima del beisbol y cuánto tiempo tardará en alcanzar esa altura?
La altura de un proyectil lanzado hacia arriba desde un montículo viene dada por la función$h(t)=−16t^{2}+96t+4$, donde t representa segundos después del lanzamiento. ¿Cuál es la altura máxima?
El beneficio en dólares generado por la producción y venta de x lámparas personalizadas viene dado por la función$P(x)=−10x^{2}+800x−12,000$. ¿Cuál es el beneficio máximo?
Los ingresos en dólares generados por la venta de un artículo en particular son modelados por la fórmula$R(x)=100x−0.0025x^{2}$, donde x representa el número de unidades vendidas. ¿Qué número de unidades se deben vender para maximizar los ingresos?
El número promedio de visitas al sitio web de una estación de radio está modelado por la fórmula$f(x)=450t^{2}−3,600t+8,000$, donde t representa el número de horas desde las 8:00 a.m. ¿A qué hora del día es mínimo el número de visitas al sitio web?
El valor en dólares de un auto nuevo es modelado por la fórmula$V(t)=125t^{2}−3,000t+22,000$, donde t representa el número de años desde que fue comprado. Determinar el valor mínimo del automóvil.
Los costos diarios de producción en dólares de una empresa de fabricación textil que produce uniformes personalizados son modelados por la fórmula$C(x)=0.02x^{2}−20x+10,000$, donde x representa el número de uniformes producidos.
1. ¿Cuántos uniformes se deben producir para minimizar los costos diarios de producción?
2. ¿Cuál es el costo mínimo de producción diario?
El área de cierta pluma rectangular viene dada por la fórmula$A=14w−w^{2}$, donde w representa el ancho en pies. Determinar el ancho que produce el área máxima.

Contestar

1. Dominio: R; rango:$[−25,∞)$

3. Dominio: R; rango:$(−∞,3]$

5. La altura máxima de 36 pies ocurre después de 1.5 segundos.

7. $4,000

9. 12:00 p.m.

11. a. 500 uniformes; b. $5,000

Ejercicio$\PageIndex{10}$ vertex by completing the square

Determinar el vértice.

$y=−(x−5)^{2}+3$
$y=−2(x−1)^{2}+7$
$y=5(x+1)^{2}+6$
$y=3(x+4)^{2}+10$
$y=−5(x+8)^{2}−1$
$y=(x+2)^{2}−5$

Contestar

1. $(5, 3)$

3. $(-1, 6)$

5. $(-8, -1)$

Ejercicio$\PageIndex{11}$ vertex by completing the square

Reescribe en$y=a(x−h)^{2}+k$ forma y determina el vértice.

$y=x^{2}−14x+24$
$y=x^{2}−12x+40$
$y=x^{2}+4x−12$
$y=x^{2}+6x−1$
$y=2x^{2}−12x−3$
$y=3x^{2}−6x+5$
$y=−x^{2}+16x+17$
$y=−x^{2}+10x$

Contestar

1. $y=(x−7)^{2}−25$; vértice:$(7, −25)$

3. $y=(x+2)^{2}−16$; vértice:$(−2, −16)$

5. $y=2(x−3)^{2}−21$; vértice:$(3, −21)$

7. $y=−(x−8)^{2}+81$; vértice:$(8, 81)$

Ejercicio$\PageIndex{12}$ vertex by completing the square

Gráfica.

$y=x^{2}−1$
$y=x^{2}+1$
$y=(x−1)^{2}$
$y=(x+1)^{2}$
$y=(x−4)^{2}−9$
$y=(x−1)^{2}−4$
$y=−2(x+1)^{2}+8$
$y=−3(x+2)^{2}+12$
$y=−5(x−1)^{2}$
$y=−(x+2)^{2}$
$y=−4(x−1)^{2}−2$
$y=9(x+1)^{2}+2$
$y=(x+5)^{2}−15$
$y=2(x−5)^{2}−3$
$y=−2(x−4)^{2}+22$
$y=2(x+3)^{2}−13$

Contestar

Captura de pantalla (268) .png — Figura$\PageIndex{32}$

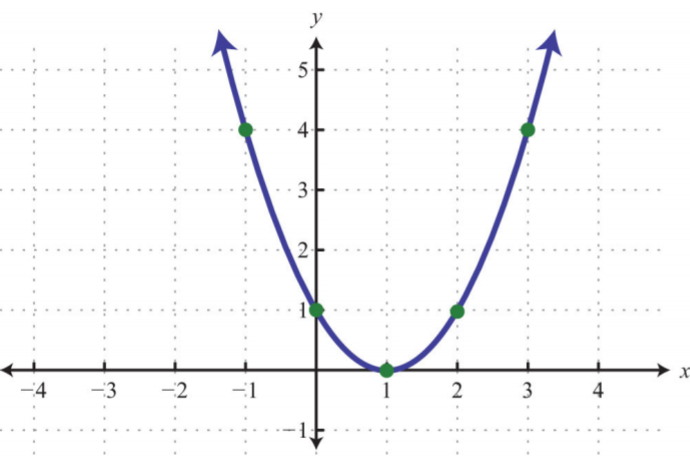Captura de pantalla (269) .png — Figura$\PageIndex{33}$

Captura de pantalla (270) .png — Figura$\PageIndex{34}$

Captura de pantalla (271) .png — Figura$\PageIndex{35}$

Captura de pantalla (272) .png — Figura$\PageIndex{36}$

11.

Captura de pantalla (273) .png — Figura$\PageIndex{37}$

13.

Captura de pantalla (274) .png — Figura$\PageIndex{38}$

15.

Captura de pantalla (275) .png — Figura$\PageIndex{39}$

Ejercicio$\PageIndex{13}$ discussion board

Anota tu plan para graficar una parábola en un examen. ¿Qué buscarás y cómo presentarás tu respuesta? Comparte tu plan en el panel de discusión.
¿Por qué cualquier parábola que se abre hacia arriba o hacia abajo es una función? Explique a un compañero de clase cómo determinar el dominio y el rango.

Contestar: 1. Las respuestas pueden variar

Search

Text Color

Text Size

Margin Size

Font Type