1.1: Revisión de números reales y valor absoluto
- Page ID
- 109820
Objetivos de aprendizaje
- Revisar el conjunto de números reales.
- Revisar la línea numérica real y la notación.
- Definir la definición geométrica y algebraica del valor absoluto.
Números Reales
El álgebra a menudo se describe como la generalización de la aritmética. El uso sistemático de las variables 1, letras utilizadas para representar números, nos permite comunicar y resolver una amplia variedad de problemas del mundo real. Por esta razón, comenzamos por revisar los números reales y sus operaciones.
Un conjunto 2 es una colección de objetos, normalmente agrupados dentro de llaves\(\{ \}\), donde cada objeto se denomina elemento 3. Al estudiar matemáticas, nos enfocamos en conjuntos especiales de números.
\[ \begin{align*} \mathbb { N } &= \underbrace{\{ 1,2,3,4,5 , \dots \}}_{\color{Cerulean}{Natural\: Numbers}} \\[4pt] W &= \underbrace{ \{ 0 , 1,2,3,4,5 , \dots \}}_{\color{Cerulean}{Whole\: Numbers}} \\[4pt] \mathbb{Z} &= \underbrace{ \{\dots ,-3,-2,-1,0,1,2,3,\dots\}}_{\color{Cerulean}{Integers}} \end{align*}\]
Los tres periodos (...) se denominan puntos suspensivos e indican que los números continúan sin límite. Un subconjunto 4, denotado\(\subseteq\), es un conjunto que consiste en elementos que pertenecen a un conjunto dado. Observe que los conjuntos de 5 naturales y números enteros 6 son ambos subconjuntos del conjunto de enteros y podemos escribir:
\(\mathbb { N } \subseteq \mathbb{Z}\)y\(W \subseteq \mathbb{Z}\)
Un conjunto sin elementos se llama el conjunto vacío 7 y tiene su propia notación especial:
\(\{\:\:\:\}=\varnothing\: \color{Cerulean}{Empty\: Set}\)
Los números racionales 8\(\mathbb{Q}\), denotados, se definen como cualquier número de la forma\(\frac { a } { b }\) donde a y b son números enteros y b es distinto de cero. Podemos describir este conjunto usando la notación de conjunto 9:
\(\mathbb { Q } = \left\{ \frac { a } { b } | a , b \in \mathbb { Z } , b \neq 0 \right\} \color{Cerulean}{Rational\: Numbers}\)
La línea vertical | dentro de las llaves lee, “tal que” y el símbolo\(\in\) indica pertenencia establecida y lee, “es un elemento de”. La notación anterior en su totalidad dice, “el conjunto de todos los números\(\frac{a}{b}\) tal que a y b son elementos del conjunto de enteros y b no es igual a cero. ” Los decimales que terminan o repiten son racionales. Por ejemplo,
\(0.05=\frac{5}{100}\)y\(0.\overline{6}=0.6666…=\frac{2}{3} \)
El conjunto de enteros es un subconjunto del conjunto de números racionales\(\mathbb{Z}\subseteq\mathbb{Q}\),, porque cada entero puede expresarse como una relación del entero y 1. En otras palabras, cualquier entero puede escribirse sobre 1 y puede considerarse un número racional. Por ejemplo,
\(7=\frac{7}{1}\)
Los números irracionales 10 se definen como cualquier número que no pueda escribirse como una relación de dos enteros. Los decimales no terminadores que no se repiten son irracionales. Por ejemplo,
\(π=3.14159…\)y\(\sqrt{2}=1.41421…\)
Por último, el conjunto de números reales 11, denotado\(\mathbb{R}\), se define como el conjunto de todos los números racionales combinados con el conjunto de todos los números irracionales. Por lo tanto, todos los números definidos hasta ahora son subconjuntos del conjunto de números reales. En resumen,

El conjunto de enteros pares 12 es el conjunto de todos los enteros que son uniformemente divisibles por\(2\). Podemos obtener el conjunto de enteros pares multiplicando cada entero por\(2\).
\(\{\dots, −6,−4,−2, 0, 2, 4, 6,\dots\} \color{Cerulean}{Even\: Integers}\)
El conjunto de enteros impares 13 es el conjunto de todos los enteros distintos de cero que no son uniformemente divisibles por\(2\).
\(\{\dots,−5,−3,−1, 1, 3, 5,\dots\} \color{Cerulean}{Odd\: Integers}\)
Un número primo 14 es un número entero mayor\(1\) que eso es divisible solo por\(1\) y por sí mismo. El número primo más pequeño es\(2\) y el resto son necesariamente impares.
\(\{2, 3, 5, 7, 11, 13, 17, 19, 23,\dots\} \color{Cerulean}{Prime\: Numbers}\)
Cualquier número entero mayor\(1\) que eso no es primo se llama número compuesto 15 y puede escribirse de manera única como un producto de primos. Cuando un número compuesto, tal como\(42\), se escribe como un producto,\(42=2⋅21\), decimos que\(2⋅21\) es una factorización 16 de\(42\) y que\(2\) y\(21\) son factores 17. Tenga en cuenta que los factores dividen el número de manera uniforme. Podemos seguir escribiendo factores compuestos como productos hasta que solo quede un producto de primos.

Por lo tanto, la factorización principal 18 de\(42\) es\(2⋅3⋅7\).
Ejemplo\(\PageIndex{1}\):
Determinar la factorización principal de\(210\).
Solución
Comience por escribir\(210\) como producto con\(10\) como factor. Después continuar factorizando hasta que sólo quede un producto de primos.
\(210=10⋅21\)
\(=2⋅5⋅3⋅7\)
\(=2⋅3⋅5⋅7\)
Dado que la factorización prima es única, no importa cómo escojamos factorizar inicialmente el número; el resultado final será el mismo.
Respuesta:
\(2⋅3⋅5⋅7\)
Una fracción 19 es un número racional escrito como cociente, o relación, de dos números enteros a y b donde\(b≠0\).

El entero por encima de la barra de fracciones se llama numerador 20 y el entero de abajo se llama denominador 21. Dos proporciones iguales expresadas usando diferentes numeradores y denominadores se denominan fracciones equivalentes 22. Por ejemplo,
\(\frac{50}{100}=\frac{1}{2}\)
Considere las siguientes factorizaciones de\(50\) y\(100\):
\(50=2⋅25\)
\(100=4⋅25\)
Los números\(50\) y\(100\) compartir el factor\(25\). Un factor compartido se denomina factor común 23. Aprovechando el hecho de que\(\frac{25}{25}=1\), tenemos
\(\frac{50}{100}=\frac{2⋅ \bcancel{25}}{4⋅\bcancel{25}}=\frac{2}{4}⋅\color{Cerulean}{1}\)\(=\frac{2}{4}\)
Dividir\(\frac{25}{25}\) y reemplazar este factor por a\(1\) se llama cancelar 24. En conjunto, estos pasos básicos para encontrar fracciones equivalentes definen el proceso de reducción de 25. Dado que los factores dividen su producto de manera uniforme, logramos el mismo resultado dividiendo tanto el numerador\(25\) como el denominador por lo siguiente:
\(\frac{ 50\color{Cerulean}{÷25}}{100\color{Cerulean}{÷25}}=\frac{2}{4}\)
Encontrar fracciones equivalentes donde el numerador y el denominador son relativamente primos 26, o no tienen otro factor común que\(1\), se llama reducir a términos más bajos 27. Esto se puede hacer dividiendo el numerador y el denominador por el mayor factor común (GCF). 28 El GCF es el mayor número que divide un conjunto de números de manera uniforme. Una forma de encontrar el GCF de\(50\) y\(100\) es enumerar todos los factores de cada uno e identificar el mayor número que aparece en ambas listas. Recuerde, cada número es también un factor de sí mismo.
\(\{1,2,5,10,25,50\} \color{Cerulean}{Factors\: of \: 50}\)
\(\{1,2,4,5,10,20,25,50,100\} \color{Cerulean}{Factors\: of \: 100}\)
Los factores comunes se enumeran en negrita, y vemos que el mayor factor común es\(50\). Utilizamos la siguiente notación para indicar el GCF de dos números: GCF\((50, 100) = 50\). Después de determinar el GCF, reduzca dividiendo tanto el numerador como el denominador de la siguiente manera:
\(\frac{50\color{Cerulean}{÷50}}{100\color{Cerulean}{÷50}}=\frac{1}{2}\)
Ejemplo\(\PageIndex{2}\):
Reducir a los términos más bajos:\(\frac{108}{72}\).
Solución
Una manera rápida de encontrar el GCF del numerador y denominador requiere que primero escribamos cada uno como producto de primos. El GCF será el producto de todos los factores primos comunes.
\(\left. \begin{array} { l } { 108 = \color{Cerulean}{2} \cdot \color{Cerulean}{2} \cdot \color{Cerulean}{3} \cdot \color{Cerulean}{3} \cdot 3 } \\ { 72 = \color{Cerulean}{2} \cdot \color{Cerulean}{2} \cdot 2 \cdot \color{Cerulean}{3} \cdot \color{Cerulean}{3} } \end{array} \right\} \operatorname { GCF } ( 108,72 ) = \color{Cerulean}{2} \cdot \color{Cerulean}{2} \cdot \color{Cerulean}{3} \cdot \color{Cerulean}{3} = 36\)
En este caso, el producto de los factores primos comunes es\(36\).
\(\frac{108}{72}=\frac{108\color{Cerulean}{÷36}}{72\color{Cerulean}{÷36}}=\frac{3}{2}\)
Podemos convertir la fracción impropia\(\frac{3}{2}\) a un número mixto\(1\frac{1}{2}\); sin embargo, es importante tener en cuenta que convertir a un número mixto no es parte del proceso de reducción. Consideramos que fracciones impropias\(\frac{3}{2}\), como, se reducen a términos más bajos. En álgebra suele ser preferible trabajar con fracciones impropias, aunque en algunas aplicaciones, los números mixtos son más apropiados.
Respuesta:
\(\frac{3}{2}\)
Recordemos la relación entre multiplicación y división:
.png)
En este caso, el dividendo 29\(12\) se divide equitativamente por el divisor 30\(6\) para obtener el cociente 31\(2\). Es cierto en general que si multiplicamos el divisor por el cociente obtenemos el dividendo. Ahora consideremos el caso donde el dividendo es cero y el divisor es distinto de cero:
\(\frac{0}{6}=0\)desde\(6⋅0=0\)
Esto demuestra que el cero dividido por cualquier número real distinto de cero debe ser cero. Ahora considere un número distinto de cero dividido por cero:
\(\frac{12}{0}= \color{Cerulean}{?}\)o\(0⋅ \color{Cerulean}{?}\)\(=12\)
Cero veces cualquier cosa es cero y concluimos que no hay un número real tal que\(0⋅?=12\). Así, el cociente\(12÷0\) es indefinido 32. Pruébalo en una calculadora, ¿qué dice? Para nuestros propósitos, simplemente escribiremos “indefinido”. Para resumir, dado cualquier número real\(a≠0\), entonces
\(0 ÷a=\frac{0}{a}=0 \color{Cerulean}{zero}\)y\(a÷ 0=\frac{a}{0}\color{Cerulean}{undefined}\)
Nos queda considerar el caso donde el dividendo y el divisor son ambos cero.
\(\frac{0}{0}=\color{Cerulean}{?}\)o\(0⋅ \color{Cerulean}{?}\)\(=0\)
Aquí, cualquier número real parece funcionar. Por ejemplo,\(0⋅5=0\) y también,\(0⋅ 3=0\). Por lo tanto, el cociente es incierto o indeterminado 33.
\(0÷0=\frac{0}{0} \color{Cerulean}{indeterminate}\)
En este curso, declaramos que\(0÷0\) es indefinido.
La línea numérica y la notación
Una línea numérica real 34, o simplemente una línea numérica, nos permite mostrar visualmente números reales asociándolos con puntos únicos en una línea. El número real asociado a un punto se denomina coordenada 35. Un punto en la recta numérica real que está asociado a una coordenada se llama su gráfica 36. Para construir una recta numérica, dibuje una línea horizontal con flechas en ambos extremos para indicar que continúa sin límite. A continuación, elija cualquier punto para representar el número cero; este punto se llama el origen 37.
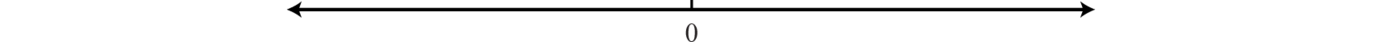
Los números reales positivos se encuentran a la derecha del origen y los números reales negativos a la izquierda. El número cero no\((0)\) es ni positivo ni negativo. Normalmente, cada tick representa una unidad.
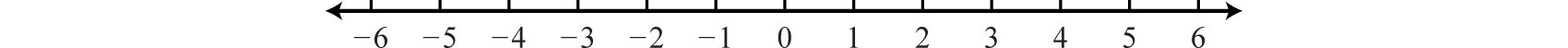
Como se ilustra a continuación, la báscula no necesita ser siempre una unidad. En la primera línea numérica, cada marca de verificación representa dos unidades. En el segundo, cada marca representa\(\frac{1}{7}\):
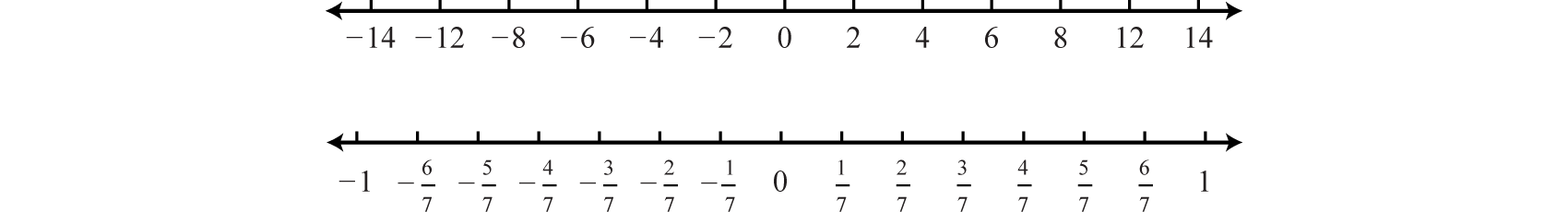
El gráfico de cada número real se muestra como un punto en el punto apropiado de la recta numérica. Un gráfico parcial del conjunto de enteros\(\mathbb{Z}\), sigue:

Ejemplo\(\PageIndex{3}\):
Grafica el siguiente conjunto de números reales:\(\{−\frac{5}{2}, 0, \frac{3}{2}, 2\}\).
Solución
Grafique los números en una recta numérica con una escala donde cada marca de verificación represente\(\frac{1}{2}\) la unidad.
Respuesta:
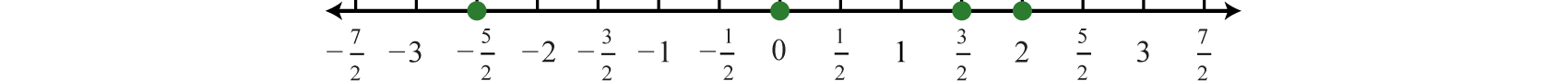
El 38 opuesto de cualquier número real a es − a. Los números reales opuestos están a la misma distancia del origen en una recta numérica, pero sus gráficas se encuentran en lados opuestos del origen y los números tienen signos opuestos.
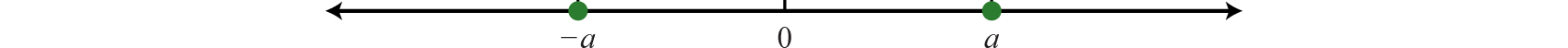
Dado el entero\(−7\), el entero a la misma distancia del origen y con el signo opuesto es\(+7\), o simplemente\(7\).

Por lo tanto, decimos que lo contrario de\(−7\) es\(−(−7) = 7\). Esta idea lleva a lo que a menudo se conoce como la propiedad doble negativa 39. Para cualquier número real a,
\(−(−a)=a\)
Ejemplo\(\PageIndex{4}\):
Calcular:\(−(−(−\frac{3}{8})).\)
Solución
Aquí aplicamos primero el doble-negativo dentro de los paréntesis más internos.
\(−(\color{Cerulean}{−(−\frac{3}{8})})=−(\frac{3}{8})\)
\(=−\frac{3}{8}\)
Respuesta:
\(−\frac{3}{8}\)
En general, un número impar de signos negativos secuenciales da como resultado un valor negativo y un número par de signos negativos secuenciales da como resultado un valor positivo.
Al comparar números reales en una recta numérica, el número mayor siempre estará a la derecha del más pequeño. Está claro que\(15\) es mayor que\(5\), pero puede que no sea tan claro ver que\(−1\) es mayor que\(−5\) hasta que graficemos cada número en una recta numérica.
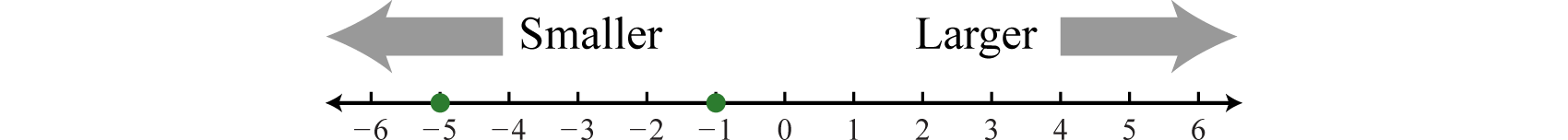
Utilizamos símbolos para ayudarnos a comunicar de manera eficiente las relaciones entre los números en la línea numérica.
\(\color{Cerulean}{Equality Relationships Order Relationships}\)
\(=\)“es igual a”\(<\) “es menor que”
\(\neq\)“no es igual a”\(>\) “es mayor que”
\(\approx\)“es aproximadamente igual a”\(\leq\) “es menor o igual a”
\(\geq\)“es mayor o igual que”
La relación entre los enteros 40 en la ilustración anterior se puede expresar de dos maneras de la siguiente manera:
\(−5<−1 \color{Cerulean}{"Negative\: five\: is\: less\: than\: negative\: one." }\)
o
\(−1>−5 \color{Cerulean}{"Negative\: one\: is\: greater\: than\: negative\: five."}\)
Los símbolos\(<\) y\(>\) se utilizan para denotar desigualdades estrictas 41, y los símbolos\(\leq\) y\(\geq\) se utilizan para denotar desigualdades inclusivas 42. En algunas situaciones, se puede aplicar correctamente más de un símbolo. Por ejemplo, las dos afirmaciones siguientes son verdaderas:
\(−10<0\)y\(−10≤0\)
Además, el componente “o igual a” de una desigualdad inclusiva nos permite escribir correctamente lo siguiente:
\(−10≤−10\)
El uso lógico de la palabra “o” requiere que sólo una de las condiciones tenga que ser cierta: el “menor que” o el “igual a”.
Ejemplo\(\PageIndex{5}\):
Rellene el espacio en blanco con\(<, =,\) o\( >: −2\) ___\(−12\).
Solución
Use\(>\) porque la gráfica de\(−2\) está a la derecha de la gráfica de\(−12\) en una recta numérica. Por lo tanto\(−2 > −12\),, que dice, “negativo dos es mayor que negativo doce. ”

Respuesta:
\(−2 > −12\)
Se lee una desigualdad algebraica 43\(x\geq 2\), tal como, “x es mayor o igual a”\(2\). Aquí la letra x es una variable, que puede representar cualquier número real. No obstante, el enunciado\(x\geq 2\) impone una condición a la variable. Las soluciones 44 son los valores para x que satisfacen la condición. Esta desigualdad tiene infinitamente muchas soluciones para x, algunas de las cuales son\(2, 3, 4.1, 5, 20,\) y\(20.001\). Dado que es imposible enumerar todas las soluciones, se necesita un sistema que permita una comunicación clara de este conjunto infinito. Las formas comunes de expresar soluciones a una desigualdad son graficándolas en una recta numérica, usando notación de intervalo o usando notación de conjunto.
Para expresar la solución gráficamente, dibuje una recta numérica y sombree en todos los valores que son soluciones a la desigualdad. A esto se le llama la gráfica del conjunto de soluciones 45. El intervalo y la notación de conjunto siguen:
“x es mayor que o igual a\(2\)"\(x\geq 2\)

\(\color{Cerulean}{Interval notation:}\)\([\, 2,∞)\)
\(\color{Cerulean}{Set notation:}\)\(\{x\in\mathbb{R} | x\geq 2\}\)
En este ejemplo, existe una desigualdad inclusiva, lo que significa que el límite inferior\(2\) se incluye en el conjunto de soluciones. Denote esto con un punto cerrado en la recta numérica y un corchete en notación de intervalo. El símbolo\(∞\) se lee como “infinito 46” e indica que el conjunto no está acotado a la derecha en una recta numérica. Si usa un teclado estándar, use (inf) como una forma abreviada para denotar infinito. Ahora compara la notación del ejemplo anterior con la de la desigualdad estricta, o no inclusiva, que sigue:
“x es menor que\(3\)"\(x<3\)

\(\color{Cerulean}{Interval\: notation:}\)\((−∞,3)\)
\(\color{Cerulean}{Set\: notation:}\)\(\{x\in\mathbb{R} | x<3\}\)
Las desigualdades estrictas implican que las soluciones pueden llegar muy cerca del punto límite, en este caso\(3\), pero en realidad no incluirlo. Denote esta idea con un punto abierto en la recta numérica y un paréntesis redondo en notación de intervalo. El símbolo\(−∞\) se lee como “infinito negativo 47” e indica que el conjunto no está acotado a la izquierda en una recta numérica. El infinito es un límite a los números reales, pero no es en sí mismo un número real: no se puede incluir en el conjunto de soluciones y por lo tanto siempre se encierra con un paréntesis.
La notación de intervalo es textual y se determina después de graficar el conjunto de soluciones en una recta numérica. Los números en notación de intervalos deben escribirse en el mismo orden en que aparecen en la recta numérica, con números más pequeños en el conjunto apareciendo primero. La notación de conjuntos, a veces llamada notación set-builder, nos permite describir el conjunto usando notación matemática familiar. Por ejemplo,
\(\{x\in\mathbb{R} | x\geq 2\}\)
Aquí,\(x\in\mathbb{R}\) describe el tipo de número. Esto implica que la variable x representa un número real. La sentencia\(x\geq 2\) es la condición que describe el conjunto usando notación matemática. En este punto de nuestro estudio del álgebra, se supone que todas las variables representan números reales. Por esta razón, se puede omitir el “\(\in\mathbb{R}\)”, y escribir
\(\{x|x\geq 2\}\)
Ejemplo\(\PageIndex{6}\):
Grafique el conjunto de soluciones y dé los equivalentes de notación de intervalo y conjunto:\(x<−20\).
Solución
Usa un punto abierto en\(−20\), debido a la estricta desigualdad\(<\), y sombrea todos los números reales a la izquierda.
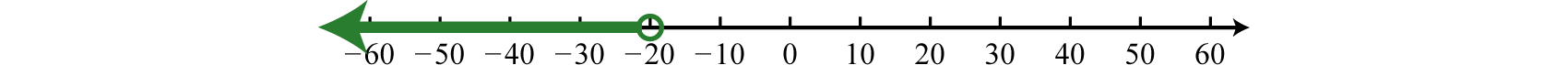
Respuesta:
Notación de intervalo:\((−∞,−20)\); notación de conjunto:\(\{x|x<−20\}\)
Una desigualdad compuesta 48 es en realidad dos o más desigualdades en una declaración unidas por la palabra “y” o por la palabra “o”. Las desigualdades compuestas con el lógico “o” requieren que se cumpla cualquiera de las dos condiciones. Por lo tanto, el conjunto de soluciones de este tipo de desigualdad compuesta consiste en todos los elementos de los conjuntos de solución de cada desigualdad. Cuando nos unimos a estos conjuntos de soluciones individuales se llama la unión 49, denotada\(\cup\). Por ejemplo,
\(x<3\)o\(x\geq 6\)
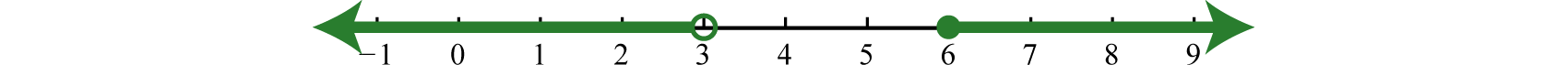
\(\color{Cerulean}{Interval notation:}\)\((−∞,3)\cup[6,∞)\)
\(\color{Cerulean}{Set notation:}\)\(\{x| x<3 or x\geq 6\}\)
Una desigualdad como,
\(−1\leq x<3\)
dice, “uno negativo es menor o igual a x y x es menor que tres”. Esto es en realidad una desigualdad compuesta porque se puede descomponer de la siguiente manera:
\(−1\leq x\)y\(x<3\)
El lógico “y” requiere que ambas condiciones sean ciertas. Ambas desigualdades serán satisfechas por todos los elementos en la intersección 50, denotada\(\cap\), de los conjuntos de solución de cada uno.
Ejemplo\(\PageIndex{7}\):
Graficar y dar la notación de intervalo equivalente:\(−1\leq x<3\).
Solución
Determine la intersección, o superposición, de los dos conjuntos de soluciones a\(x<3\) y\(x\geq −1\). Las soluciones a cada desigualdad se esbozan por encima de la recta numérica como medio para determinar la intersección, la cual se grafica en la recta numérica de abajo.
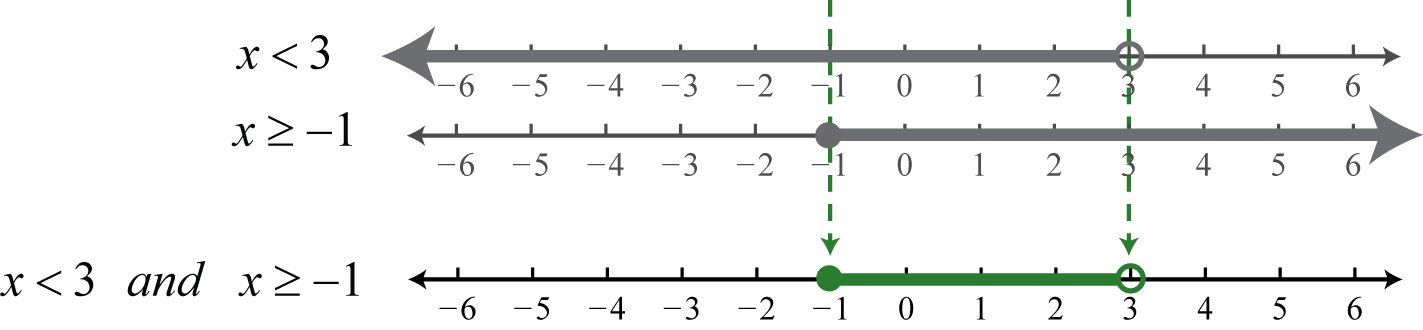
Aquí, no\(3\) es una solución porque resuelve sólo una de las desigualdades. Alternativamente, podemos interpretar\(−1\leq x<3\) como todos los valores posibles para x entre, o delimitado por,\(−1\) y\(3\) donde\(−1\) se incluye en el conjunto de soluciones.
Respuesta:
Notación de intervalo:\([\,−1, 3)\); notación de conjunto:\(\{x|−1\leq x<3\}\)
En este texto, a menudo señalaremos la notación equivalente utilizada para expresar cantidades matemáticas electrónicamente usando los símbolos estándar disponibles en un teclado.
\(× " * " ≥ " >= "\)
\(÷ " / " ≤ " <= " \)
\( ≠ " != "\)
Muchas calculadoras, sistemas de álgebra computacional y lenguajes de programación utilizan la notación presentada anteriormente, entre comillas.
Valor Absoluto
El valor absoluto 51 de un número real a, denotado\(|a|\), se define como la distancia entre cero (el origen) y la gráfica de ese número real en la recta numérica. Al ser una distancia, siempre es positiva. Por ejemplo,
\(|−4|=4\)y\(|4|=4\)
Ambos\(4\) y\(−4\) son cuatro unidades del origen, como se ilustra a continuación:
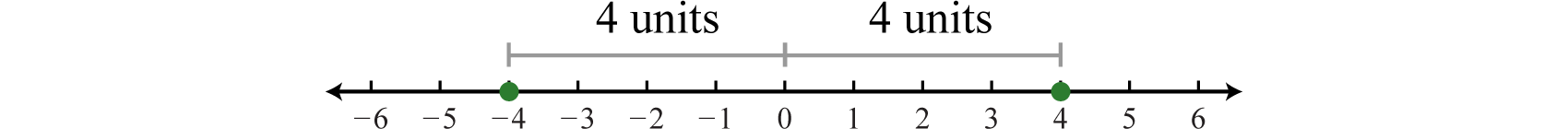
Asimismo, cabe señalar que,
\(|0|=0\)
La definición algebraica del valor absoluto de un número real a sigue:
\(| a | = \left\{ \begin{aligned} a & \text { if } a \geq 0 \\ - a & \text { if } a < 0 \end{aligned} \right.\)
A esto se le llama una definición por partes 52. El resultado depende de la cantidad a. Si a no es negativo, como lo indica la desigualdad\(a\geq 0\), entonces el valor absoluto será ese número a. Si a es negativo, como lo indica la desigualdad\(a<0\), entonces el valor absoluto será el opuesto de ese número, − a. Los resultados serán los mismos que la definición geométrica. Por ejemplo, para determinar\(|−4|\) tomamos nota de que el valor es negativo y utilizamos la segunda parte de la definición. El valor absoluto será lo contrario de\(−4\).
\(|−4|=−(−4)\)
\(=4\)
En este punto, podemos determinar qué números reales tienen ciertos valores absolutos.
Ejemplo\(\PageIndex{8}\):
Determinar los valores representados por\(x: | x |=6\).
Solución
Piense en un número real cuya distancia al origen sea de 6 unidades. Hay dos soluciones: la distancia a la derecha del origen y la distancia a la izquierda del origen, a saber\(\{±6\}\). El símbolo\(±\) se lee “más o menos” e indica que hay dos respuestas, una positiva y otra negativa.
\(|−6|=6\)y\(|6|=6\)
Respuesta:
x=±6
Ejemplo\(\PageIndex{9}\):
Determinar los valores representados por\(x: | x |=−6\).
Solución
Aquí deseamos encontrar un valor donde la distancia al origen sea negativa. Dado que la distancia negativa no está definida, esta ecuación no tiene solución. Usa el conjunto vacío\(Ø\) para denotar esto.
Respuesta:
\(Ø\)
El valor absoluto se puede expresar textualmente usando la notación abs (a). A menudo nos encontramos con valores absolutos negativos, como\(−|3|\) o\(−abs(3)\). Observe que el signo negativo está delante del símbolo de valor absoluto. En este caso, trabajar primero el valor absoluto y luego encontrar lo contrario del resultado.
\(\begin{array} { r r r } { - | 3 | } & { } & { - | - 3 | } \\ { \color{Cerulean}{\downarrow} } & { \text { and } } & { \color{Cerulean}{\downarrow} } \\ { = - 3 } & { } & { = - 3 } \end{array}\)
Trate de no confundir esto con la propiedad doble negativa, que establece que\(− (−3) = +3\).
Ejemplo\(\PageIndex{10}\):
Simplificar:\(−(−|−50|)\).
Solución
Primero, encuentre el valor absoluto de\(−50\) y luego aplique la propiedad doble-negativa.
\(−(−\color{Cerulean}{|−50|}\)\( )=−(−50)\)
\(=50\)
Respuesta:
\(50\)
Claves para llevar
- El álgebra a menudo se describe como la generalización de la aritmética. El uso sistemático de variables, utilizadas para representar números reales, nos permite comunicar y resolver una amplia variedad de problemas del mundo real. Por lo tanto, es importante revisar los subconjuntos de números reales y sus propiedades.
- La línea numérica nos permite mostrar visualmente números reales asociándolos con puntos únicos en una línea.
- La notación especial se utiliza para comunicar relaciones de igualdad y orden entre números en una recta numérica.
- El valor absoluto de un número real se define geométricamente como la distancia entre cero y la gráfica de ese número en una recta numérica. Alternativamente, el valor absoluto de un número real se define algebraicamente de manera fragmentada. Si un número real a no es negativo, entonces el valor absoluto será ese número a. Si a es negativo, entonces el valor absoluto será el opuesto de ese número, − a.
Ejercicio\(\PageIndex{1}\)
Utilice la notación de conjunto para enumerar los elementos descritos.
- Cada otro número impar positivo hasta\(21\).
- Cada otro número par positivo hasta\(22\).
- Los números primos pares.
- Números racionales que también son irracionales.
- El conjunto de enteros negativos.
- El conjunto de enteros pares negativos.
- Tres enteros impares consecutivos comenzando con\(13\).
- Tres enteros pares consecutivos comenzando con\(22\).
- Contestar
-
1. \(\{1, 5, 9, 13, 17, 21\}\)
3. \(\{2\}\)
5. \(\{\dots,−3, −2, −1\}\)
7. \(\{13, 15, 17\}\)
Ejercicio\(\PageIndex{2}\)
Determinar la factorización primo del número compuesto dado.
- \(195\)
- \(78\)
- \(330\)
- \(273\)
- \(180\)
- \(350\)
- Contestar
-
1. \(3⋅5⋅13\)
3. \(2⋅3⋅5⋅11\)
5. \(2⋅2⋅3⋅3⋅5\)
Ejercicio\(\PageIndex{3}\)
Reducir a los términos más bajos.
- \(\frac{42}{30}\)
- \(\frac{105}{70}\)
- \(\frac{84}{120}\)
- \(\frac{315}{420}\)
- \(\frac{60}{45}\)
- \(\frac{144}{120}\)
- \(\frac{64}{128}\)
- \(\frac{72}{216}\)
- \(\frac{0}{25}\)
- \(\frac{33}{0}\)
- Contestar
-
1. \(\frac{7}{5}\)
3. \(\frac{7}{10}\)
5. \(\frac{4}{3}\)
7. \(\frac{1}{2}\)
9. \(0\)
Ejercicio\(\PageIndex{4}\)
Grafica los siguientes conjuntos de números.
- \(\{−5, 5, 10, 15\}\)
- \(\{−4, −2, 0, 2, 4\}\)
- \(\{−\frac{3}{2},−\frac{1}{2}, 0, 1, 2\}\)
- \(\{−\frac{3}{4},−\frac{1}{4}, 0, \frac{1}{2}, \frac{3}{4}\}\)
- \(\{−5,−4,−3,−1, 1\}\)
- \(\{−40, −30, −20, 10, 30\}\)
- Contestar
-

Figura\(\PageIndex{19}\) 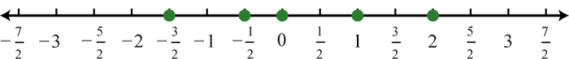
Figura\(\PageIndex{20}\) 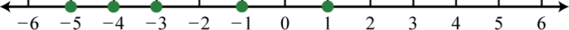
Figura\(\PageIndex{21}\)
Ejercicio\(\PageIndex{5}\)
Simplificar.
- \(−(−10)\)
- \(−(−\frac{3}{5})\)
- \(−(−(−12))\)
- \(−(−(−\frac{5}{3}))\)
- \(−(−(−(−\frac{1}{2})))\)
- \(−(−(−(−(−\frac{3}{4}))))\)
- Contestar
-
1. \(10\)
3. \(−12\)
5. \(\frac{1}{2}\)
Ejercicio\(\PageIndex{6}\)
Rellene el espacio en blanco con\(<, =, or >\).
- \(−10\)_____\(−15\)
- \(−101\)_____\(−100\)
- \(−33\)_____\(0\)
- \(0\)_____\(−50\)
- \(−(−(−2))\)_____\(−(−3)\)
- \(−(−(−\frac{1}{2}))\)_____\(−\frac{1}{4}\)
- \(−(−(−\frac{2}{3}))\)_____\(−(−\frac{1}{2})\)
- \(−(−\frac{2}{3})\)_____\(−(−(−(−\frac{2}{3})))\)
- Contestar
-
1. \(>\)
3. \(<\)
5. \(<\)
7. \(<\)
Ejercicio\(\PageIndex{7}\)
Verdadero o Falso.
- \(0=0\)
- \(5\leq 5\)
- \(1.0\overline{32}\)es irracional.
- \(0\)es un número no negativo.
- Cualquier entero es un número racional.
- La constante\(π\) es racional.
- Contestar
-
1. Cierto
3. Falso
5. Cierto
Ejercicio\(\PageIndex{8}\)
Grafique el conjunto de soluciones y dé la notación de intervalo equivalente.
- \(x<−1\)
- \(x>−3\)
- \(x\geq −8\)
- \(x\leq 6\)
- \(−10\leq x<4\)
- \(3<x\leq 7\)
- \(−40<x<0\)
- \(−12\leq x\leq −4\)
- \(x<5\)y\(x\geq 0\)
- \(x\leq −10\)y\(x\geq −40\)
- \(x\leq 7\)y\(x<10\)
- \(x<1\)y\(x>3\)
- \(x<−2\)o\(x\geq 5\)
- \(x\leq 0\)o\(x\geq 4\)
- \(x<6\)o\(x>2\)
- \(x<0\)o\(x\leq 5\)
- Contestar
-
1. \((−∞, −1)\);
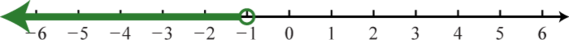
Figura\(\PageIndex{22}\) 3. \([8,∞)\);

Figura\(\PageIndex{23}\) 5. \([−10,4)\);

Figura\(\PageIndex{24}\) 7. \((−40,0)\);

Figura\(\PageIndex{25}\) 9. \([0,5)\);

Figura\(\PageIndex{26}\) 11. \((−∞,7)\);

Figura\(\PageIndex{27}\) 13. \((−∞,−2)\cup [5,∞)\);
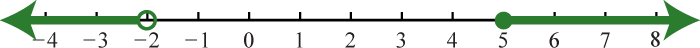
Figura\(\PageIndex{28}\) 15. \((−∞,∞)=\mathbb{R}\);

Figura\(\PageIndex{29}\)
Ejercicio\(\PageIndex{9}\)
Escribir una desigualdad equivalente.
- Todos los números reales menores que\(−15\).
- Todos los números reales mayores o iguales a\(−7\).
- Todos los números reales menores\(6\) y mayores que cero.
- Todos los números reales menores a cero y mayores que\(−5\).
- Todos los números reales menores o iguales\(5\) o mayores que\(10\).
- Todos los números reales entre\(−2\) y\(2\).
- Contestar
-
1. \(x<−15\)
3. \(0<x<6\)
5. \(x\leq 5\)o\(x>10\)
Ejercicio\(\PageIndex{10}\)
Determinar la desigualdad dadas las respuestas expresadas en notación de intervalos.
- \((−∞,12)\)
- \([−8,∞)\)
- \((−∞,0]\)
- \((0,∞)\)
- \((−6,14)\)
- \((0,12]\)
- \([5,25)\)
- \([−30,−10]\)
- \((−∞,2)\cup [3,∞)\)
- \((−∞,−19]\cup [−12,∞)\)
- \((−∞,−2)\cup (0,∞)\)
- \((−∞,−15]\cup (−5,∞)\)
- Contestar
-
1. \(x<12\)
3. \(x\leq 0\)
5. \(−6<x<14\)
7. \(5\leq x<25\)
9. \(x<2\)o\(x\geq 3\)
11. \(x<−2\)o\(x>0\)
Ejercicio\(\PageIndex{11}\)
Simplificar.
- \(|−9|\)
- \(|14|\)
- \(−|−4|\)
- \(−|8|\)
- \(−|−\frac{5}{8}|\)
- \(−(−|\frac{7}{2}|)\)
- \(−|−(−7)|\)
- \(−|−(−10)|\)
- \(−(−|−2|)\)
- \(−(−|−10|)\)
- \(−(−|−(−5)|)\)
- \(−(−(−|−20|))\)
- Contestar
-
1. \(9\)
3. \(−4\)
5. \(−\frac{5}{8}\)
7. \(−7\)
9. \(2\)
11. \(5\)
Ejercicio\(\PageIndex{12}\)
Determinar los valores representados por a.
- \(|a|=10\)
- \(|a|=7\)
- \(|a|=\frac{1}{2}\)
- \(|a|=\frac{9}{4}\)
- \(|a|=0\)
- \(|a|=−1\)
- Contestar
-
1. \(a=±10\)
3. \(a=±\frac{1}{2}\)
5. \(a=0\)
Ejercicio\(\PageIndex{13}\)
- Investigar y discutir los orígenes y evolución del álgebra.
- Investigar y discutir las razones por las que el álgebra es un tema obligatorio hoy
- Los conjuntos de soluciones a desigualdades se pueden expresar usando una gráfica, notación de intervalos o notación de conjuntos. Discutir los méritos e inconvenientes de cada método. ¿Cuál prefieres?
- Investigar y discutir el Teorema Fundamental del Álgebra. Ilustra su idea con un ejemplo y comparte tus resultados.
- Contestar
-
1. La respuesta puede variar
3. La respuesta puede variar
Notas al pie
1 Letras utilizadas para representar números.
2 Cualquier colección de objetos.
3 Un objeto dentro de un conjunto.
4 Un conjunto que consiste en elementos que pertenecen a un conjunto dado.
5 El conjunto de números de conteo:\(\{1, 2, 3, 4, 5, \dots\}\).
6 El conjunto de números naturales combinado con cero:\(\{0, 1, 2, 3, 4, 5,\dots\}\).
7 Un subconjunto sin elementos, denotado\(Ø\) o\(\{ \}\).
8 Números de la forma\(\frac{a}{b}\), donde a y b son números enteros y b es distinto de cero.
9 Notación utilizada para describir un conjunto usando símbolos matemáticos.
10 Números que no se pueden escribir como una relación de dos enteros.
11 El conjunto de todos los números racionales e irracionales.
12 Enteros que son divisibles por\(2\).
13 enteros distintos de cero que no son divisibles por\(2\).
14 Entero mayor que\(1\) eso es divisible solo por\(1\) y por sí mismo.
15 Los enteros mayores que\(1\) eso no son primos.
16 Cualquier combinación de factores, multiplicados entre sí, dando como resultado el producto.
17 Cualquiera de los números que forman un producto.
18 La factorización única de un número natural escrito como producto de primos.
19 Un número racional escrito como cociente de dos enteros:\({a}{b}\), donde\(b ≠ 0\).
20 El número por encima de la barra de fracción.
21 El número por debajo de la barra de fracción. \
22 Dos fracciones iguales expresadas usando diferentes numeradores y denominadores.
23 Un factor que es compartido por más de un número real.
24 El proceso de dividir los factores comunes en el numerador y el denominador.
25 El proceso de encontrar fracciones equivalentes dividiendo el numerador y el denominador por factores comunes.
26 Números que no tienen otro factor común que no sea\(1\).
27 Encontrar fracciones equivalentes donde el numerador y el denominador no comparten ningún factor entero común que no sea\(1\).
28 El mayor factor compartido de cualquier número de enteros.
29 Un número a dividir por otro número.
30 El número que se divide en el dividendo.
31 El resultado de la división.
32 Un cociente como\(\frac{5}{0}\) se deja sin sentido y no se le asigna una interpretación.
33 Un cociente como\(\frac{0}{0}\) es una cantidad que es incierta o ambigua.
34 Una línea que nos permite representar visualmente números reales asociándolos con puntos en la línea.
35 El número real asociado a un punto en una recta numérica.
36 Un punto en la recta numérica asociado a una coordenada.
37 El punto en la recta numérica que representa cero.
38 Números reales cuyas gráficas se encuentran en lados opuestos del origen con la misma distancia al origen.
39 Lo contrario de un número negativo es positivo:\(−(−a) = a\).
40 El conjunto de números enteros positivos y negativos combinados con cero:\(\{\dots , −3, −2, −1, 0, 1, 2, 3, \dots\}\).
41 Relaciones de orden expresas usando el símbolo\(<\) para “menor que” y\(>\) para “mayor que”.
42 Utilice el símbolo\(≤\) para expresar cantidades que sean “menores o iguales a” y\(≥\) para cantidades que sean “mayores o iguales” entre sí.
43 Expresiones algebraicas relacionadas con los símbolos\(≤, <, \geq\) y\(>\).
44 Valores que se pueden utilizar en lugar de la variable para satisfacer la condición dada.
45 Soluciones a una expresión algebraica expresada en una recta numérica.
46 El símbolo\(∞\) indica que el intervalo no está acotado a la derecha.
47 El símbolo\(−∞\) indica que el intervalo no está acotado a la izquierda.
48 Dos o más desigualdades en una declaración unidas por la palabra “y” o por la palabra “o”.
49 El conjunto formado por la unión de los conjuntos de solución individuales indicados por el uso lógico de la palabra “o” y denotados con el símbolo\(\cup\).
50 El conjunto formado por los valores compartidos de los conjuntos de soluciones individuales que se indica mediante el uso lógico de la palabra “y”, denotada con el símbolo\(\cap\).
51 El valor absoluto de un número representa la distancia desde la gráfica del número a cero en una recta numérica.
52 Una definición que cambia dependiendo del valor de la variable.


