2.5: Uso de transformaciones para graficar funciones
( \newcommand{\kernel}{\mathrm{null}\,}\)
Objetivos de aprendizaje
- Definir las transformaciones rígidas y utilizarlas para bosquejar gráficas.
- Defina las transformaciones no rígidas y utilícelas para bosquejar gráficas.
Traducciones Verticales y Horizontales
Cuando la gráfica de una función se cambia en apariencia y/o ubicación la llamamos transformación. Hay dos tipos de transformaciones. Una transformación rígida 57 cambia la ubicación de la función en un plano de coordenadas, pero deja sin cambios el tamaño y la forma de la gráfica. Una transformación no rígida 58 cambia el tamaño y/o la forma de la gráfica.
Una traslación vertical 59 es una transformación rígida que desplaza una gráfica hacia arriba o hacia abajo en relación con la gráfica original. Esto ocurre cuando se agrega una constante a cualquier función. Si agregamos una constante positiva a caday coordenada, la gráfica se desplazará hacia arriba. Si agregamos una constante negativa, la gráfica se desplazará hacia abajo. Por ejemplo, considere las funcionesg(x)=x2−3 yh(x)=x2+3. Comience evaluando para algunos valores de la variable independientex.
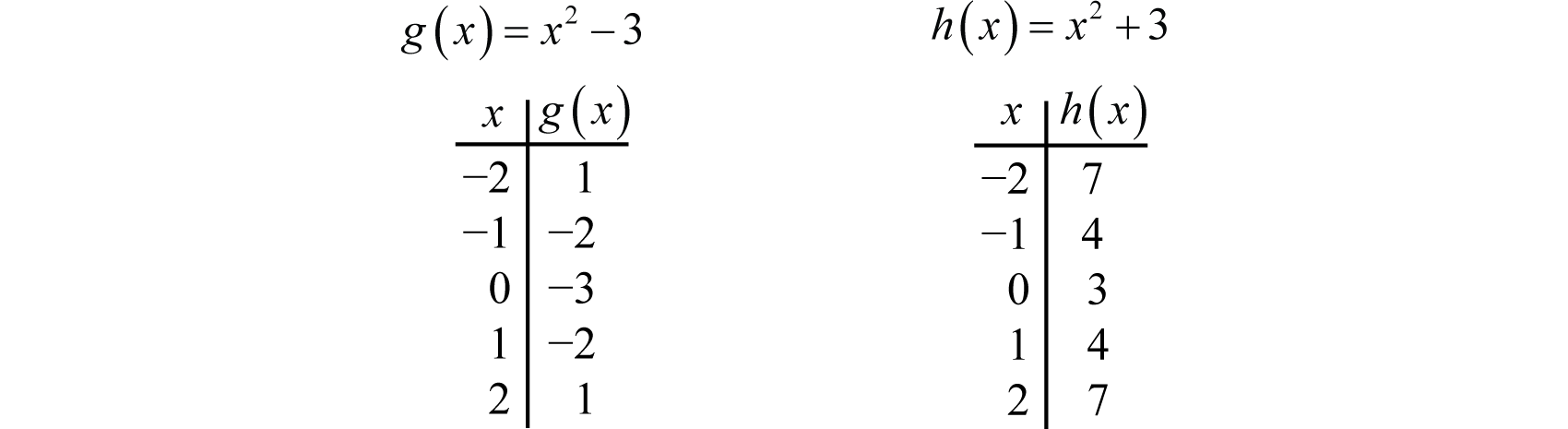
Ahora grafica los puntos y compara las gráficas de las funcionesg yh con la gráfica básica def(x)=x2, que se muestra usando una curva gris discontinua a continuación.
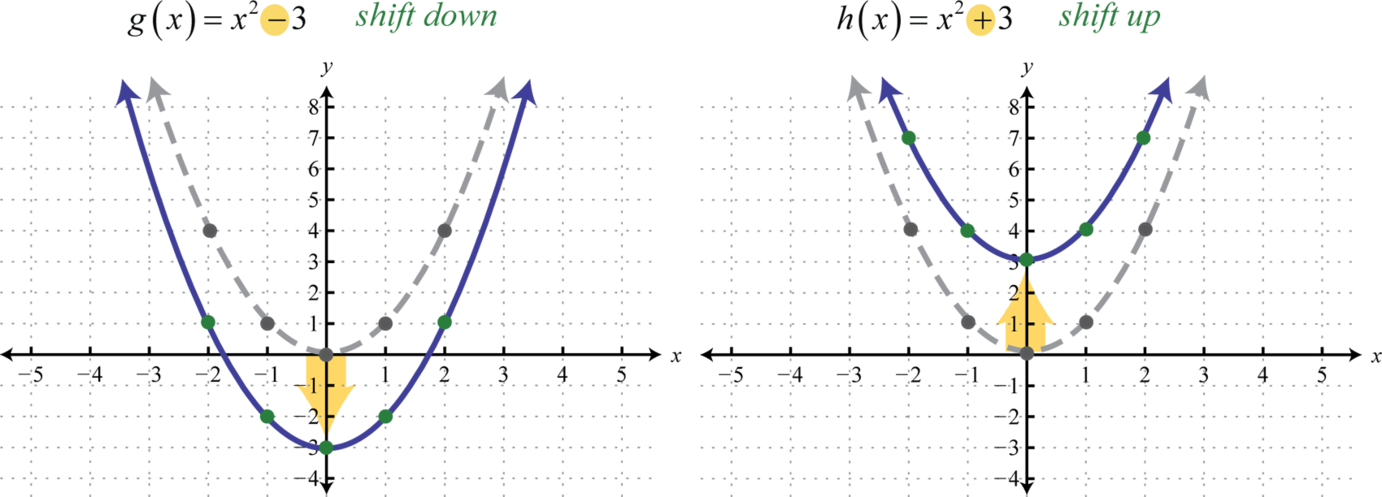
La funcióng desplaza la gráfica básica hacia abajo3 unidades y la funciónh desplaza la gráfica básica hacia arriba3 unidades. En general, esto describe las traducciones verticales; sik hay algún número real positivo:
| kUnidades de cambio vertical hacia arriba: | F(x)=f(x)+k |
|---|---|
| kUnidades de cambio vertical hacia abajo: | F(x)=f(x)−k |
Ejemplo2.5.1:
Esbozar la gráfica deg(x)=√x+4.
Solución
Comience con la función básica definida porf(x)=√x y desplace la gráfica hacia arriba4 unidades.
Respuesta:
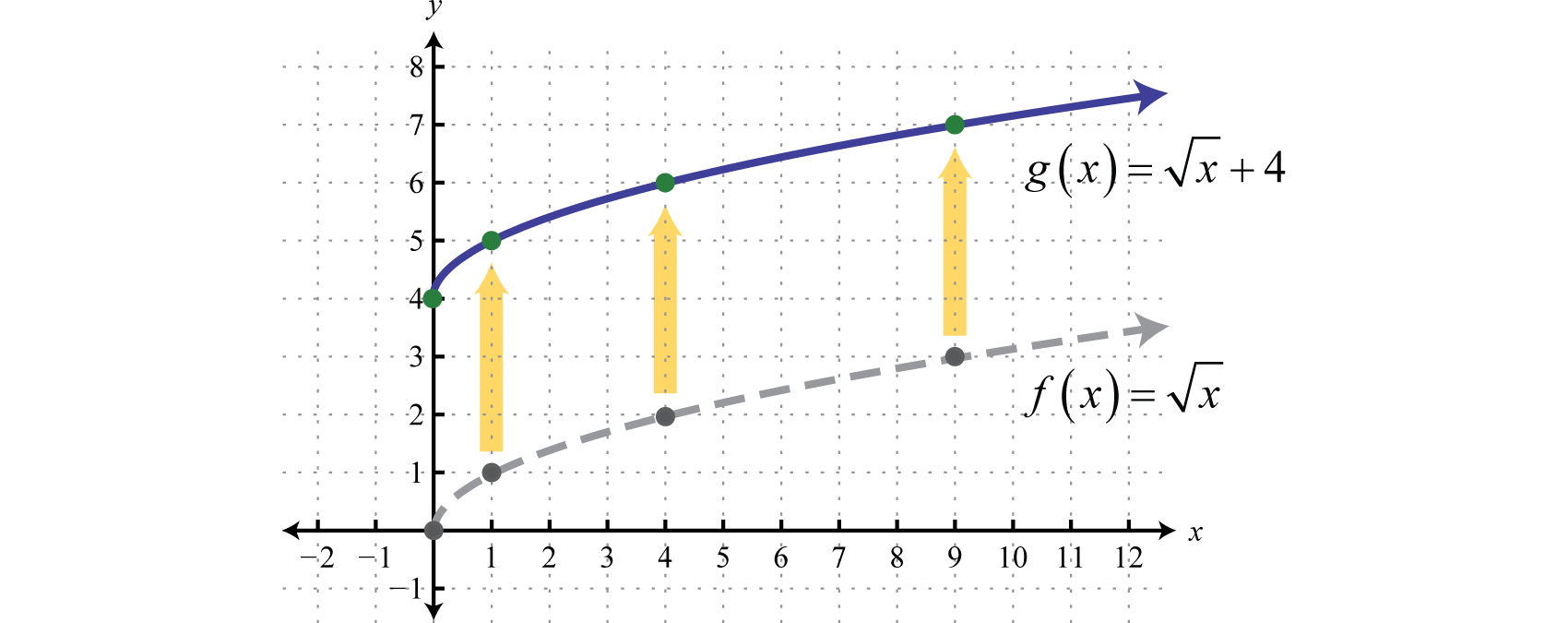
Una traslación horizontal 60 es una transformación rígida que desplaza una gráfica a la izquierda o a la derecha en relación con la gráfica original. Esto ocurre cuando sumamos o restamos constantes de lax coordenada -antes de aplicar la función. Por ejemplo, considere las funciones definidas porg(x)=(x+3)2 yh(x)=(x−3)2 y cree las siguientes tablas:
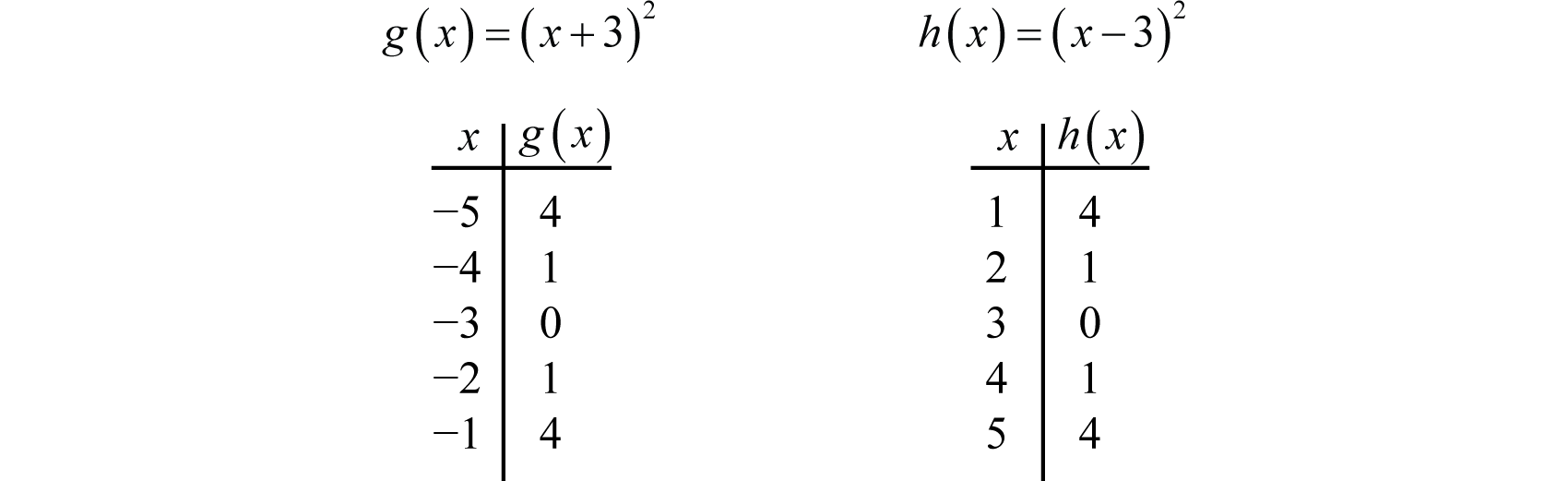
Aquí sumamos y restamos de las coordenadas x y luego cuadramos el resultado. Esto produce una traslación horizontal.
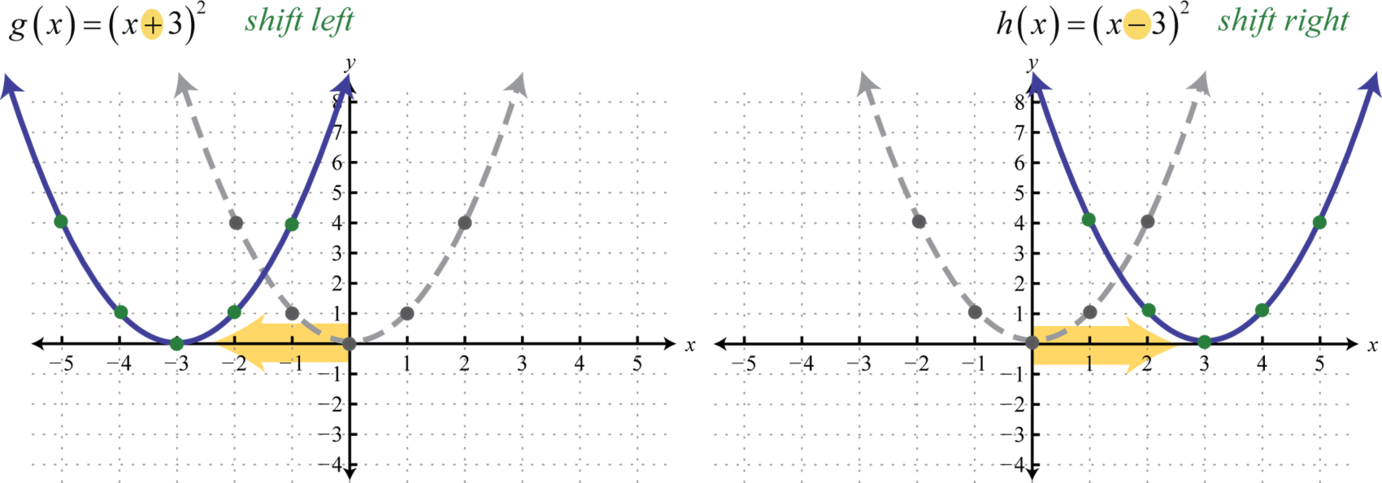
Tenga en cuenta que esto es lo contrario de lo que podría esperar. En general, esto describe las traducciones horizontales; sih hay algún número real positivo:
| hUnidades de desplazamiento horizontal a la izquierda: | F(x)=f(x+h) |
|---|---|
| hUnidades de desplazamiento horizontal a la derecha: | F(x)=f(x−h) |
Ejemplo2.5.2:
Esbozar la gráfica deg(x)=(x−4)3.
Solución
Comience con una función básica de cubo definida porf(x)=x3 y desplace las4 unidades gráficas hacia la derecha.
Respuesta:
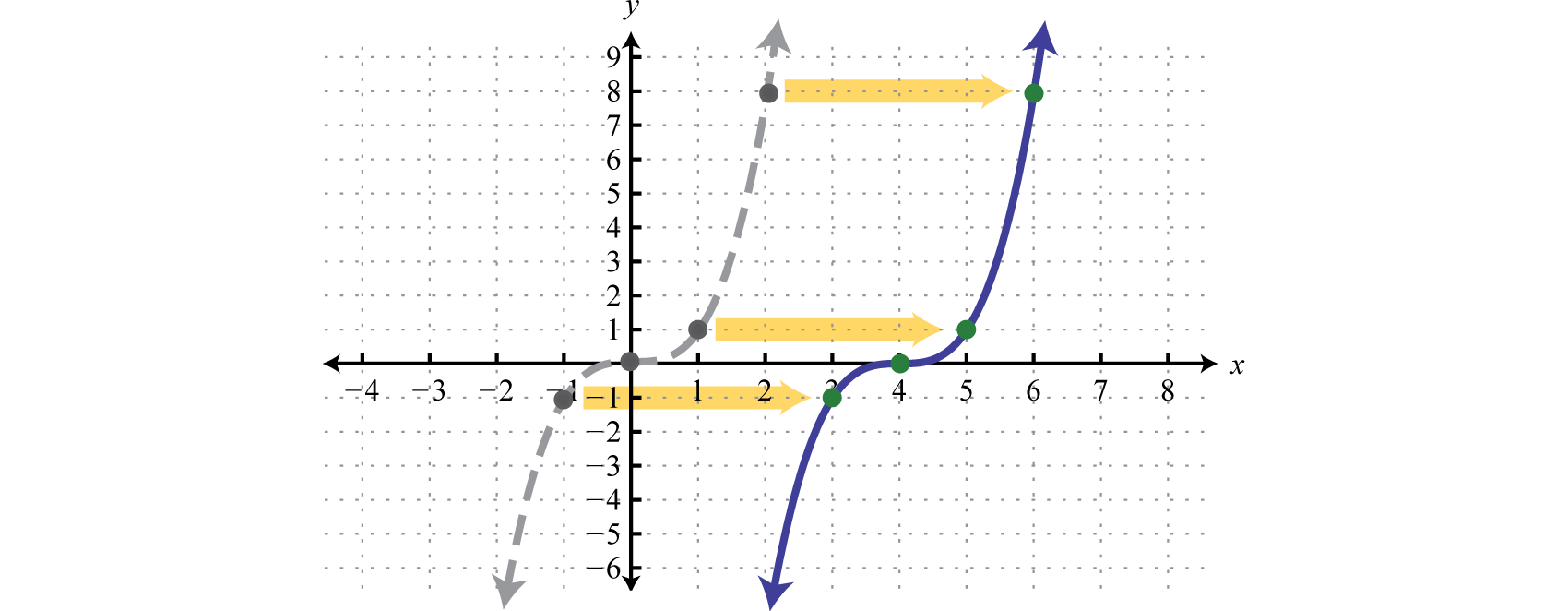
A menudo ocurre que se producen combinaciones de traducciones.
Ejemplo2.5.3:
Esbozar la gráfica deg(x)=|x+3|−5.
Solución
Comience con la función de valor absoluto y aplique las siguientes transformaciones.
y=|x|Basicfunctiony=|x+3|Horizontalshiftleft3unitsy=|x+3|−5Verticalshiftdown5units
Respuesta:
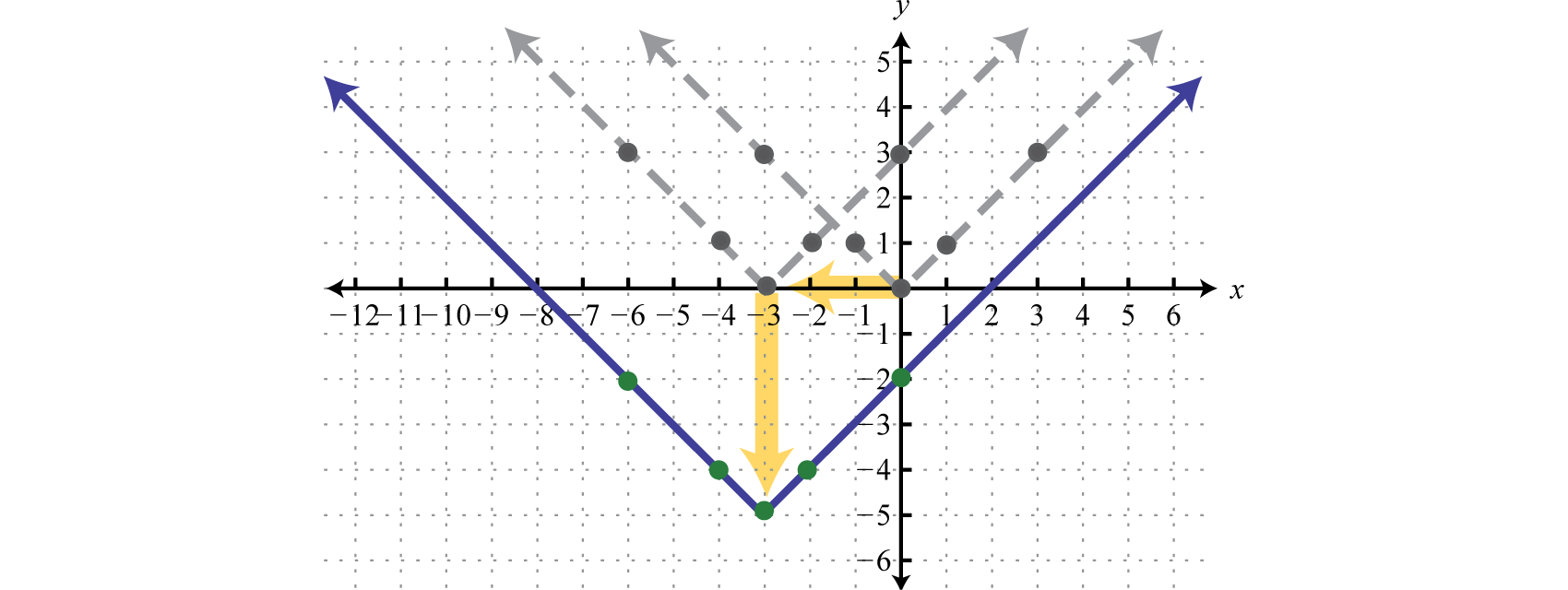
El orden en el que aplicamos las traducciones horizontales y verticales no afecta a la gráfica final.
Ejemplo2.5.4:
Esbozar la gráfica deg(x)=1x−5+3.
Solución
Empezar con la función recíproca e identificar las traducciones.
y=1xBasicfunctiony=1x−5Horizontalshiftleft3unitsy=1x−5+3Verticalshiftdown5units
Tenga cuidado de desplazar la asíntota vertical del eje y 5 unidades a la derecha y desplazar la asíntota horizontal del eje x hacia arriba 3 unidades.
Respuesta:
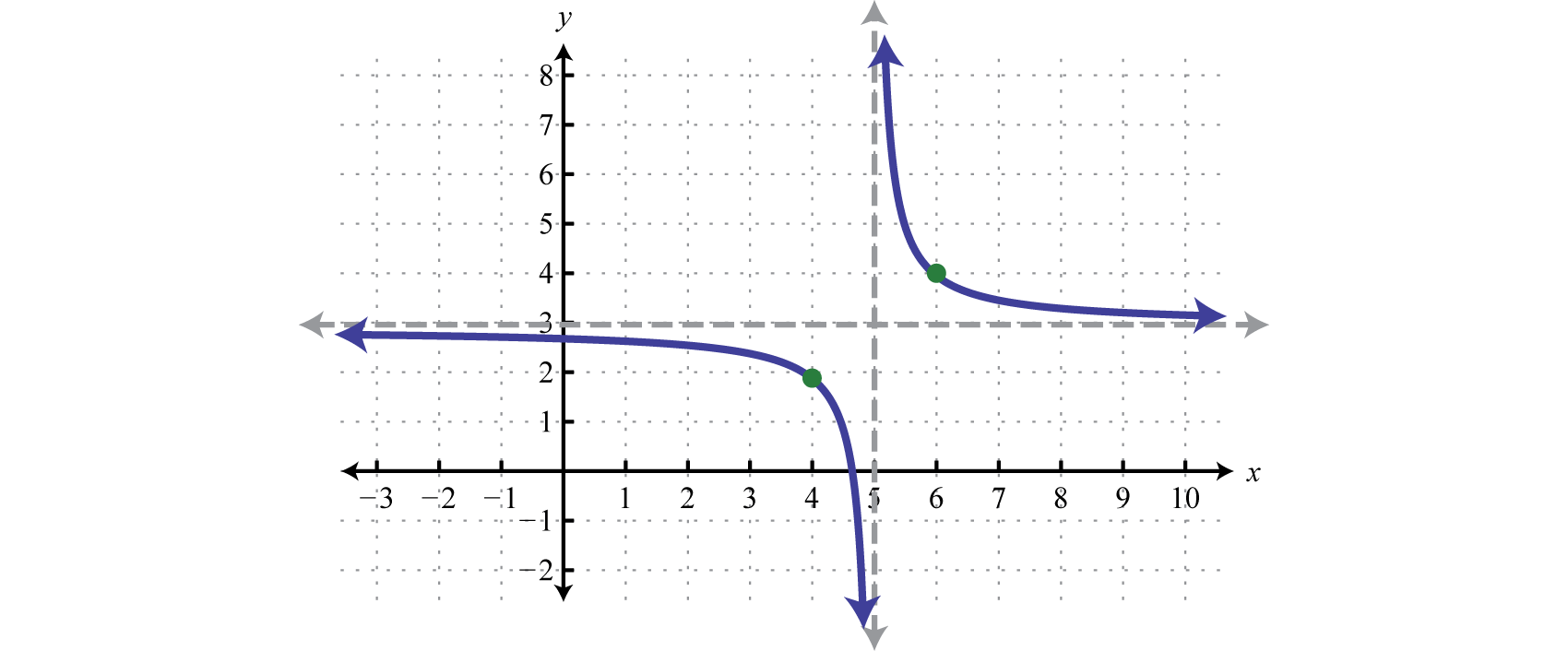
Ejercicio2.5.1
Esbozar la gráfica deg(x)=(x−2)2+1.
- Responder
-
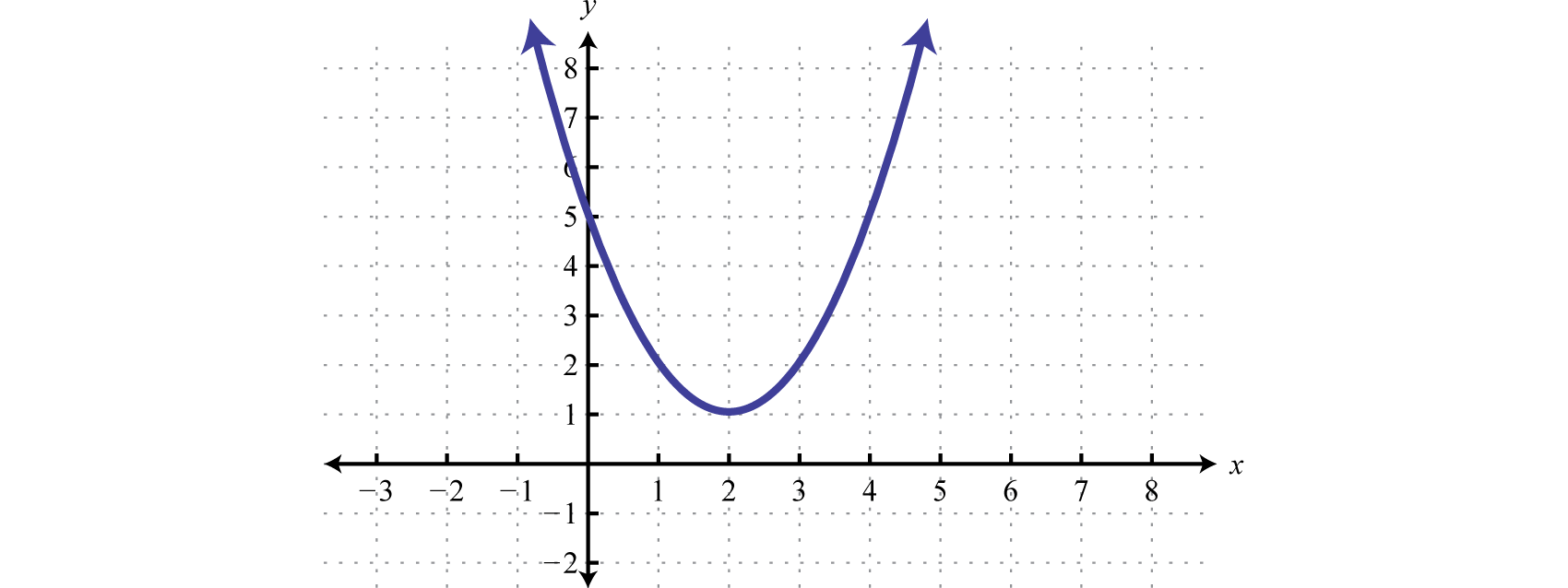
Figura2.5.9 www.youtube.com/v/6f6zkaogxte
Reflexiones
Una reflexión 61 es una transformación en la que se produce una imagen especular de la gráfica alrededor de un eje. En esta sección, consideraremos reflexiones sobre el ejex - yy -eje. La gráfica de una función se refleja alrededor del ejex - si caday coordenada se multiplica por−1. La gráfica de una función se refleja alrededor dely eje -si cadax coordenada se multiplica por−1 antes de aplicar la función. Por ejemplo, considereg(x)=√−x yh(x)=−√x.

Compare la gráfica deg yh con la función básica de raíz cuadrada definida porf(x)=√x, que se muestra discontinua en gris a continuación:

La primera funcióng tiene un factor negativo que aparece “dentro” de la función; esto produce una reflexión sobre ely eje -eje. La segunda funciónh tiene un factor negativo que aparece “fuera” de la función; esto produce una reflexión sobre elx eje -eje. En general, es cierto que:
| Reflexión sobre ely eje: | F(x)=f(−x) |
|---|---|
| Reflexión sobre elx eje: | F(x)=−f(x) |
Al bosquejar gráficas que involucren una reflexión, considere primero la reflexión y luego aplique las traducciones verticales y/u horizontales.
Ejemplo2.5.5:
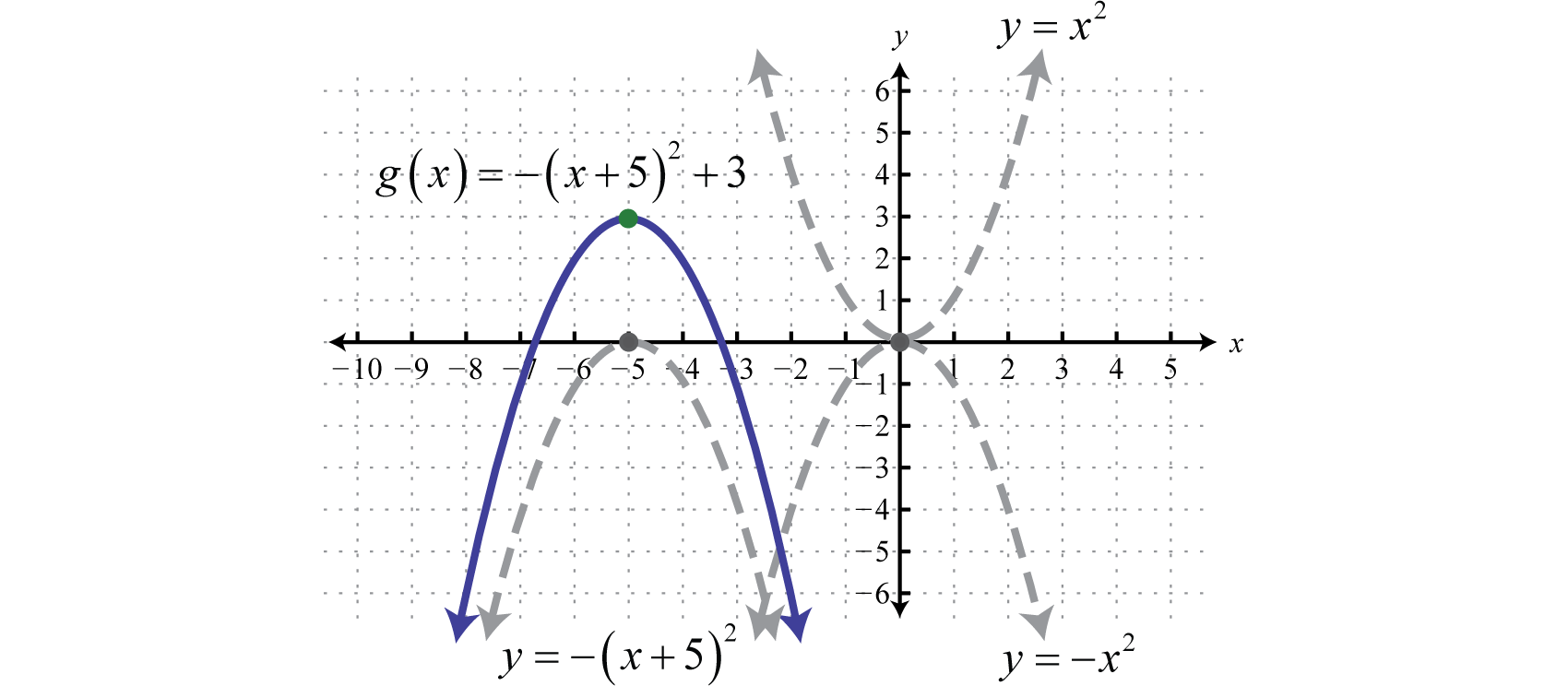
Esbozar la gráfica deg(x)=−(x+5)2+3.
Solución
Comience con la función de cuadratura y luego identifique las transformaciones comenzando con cualquier reflexión.
y=x2Basicfunction.y=−x2Relfectionaboutthex−axis.y=−(x+5)2Horizontalshiftleft5units.y=−(x+5)2+3Verticalshiftup3units.
Usa estas traducciones para bosquejar la gráfica.
Respuesta:
Ejercicio2.5.2
Esbozar la gráfica deg(x)=−|x|+3.
- Responder
-
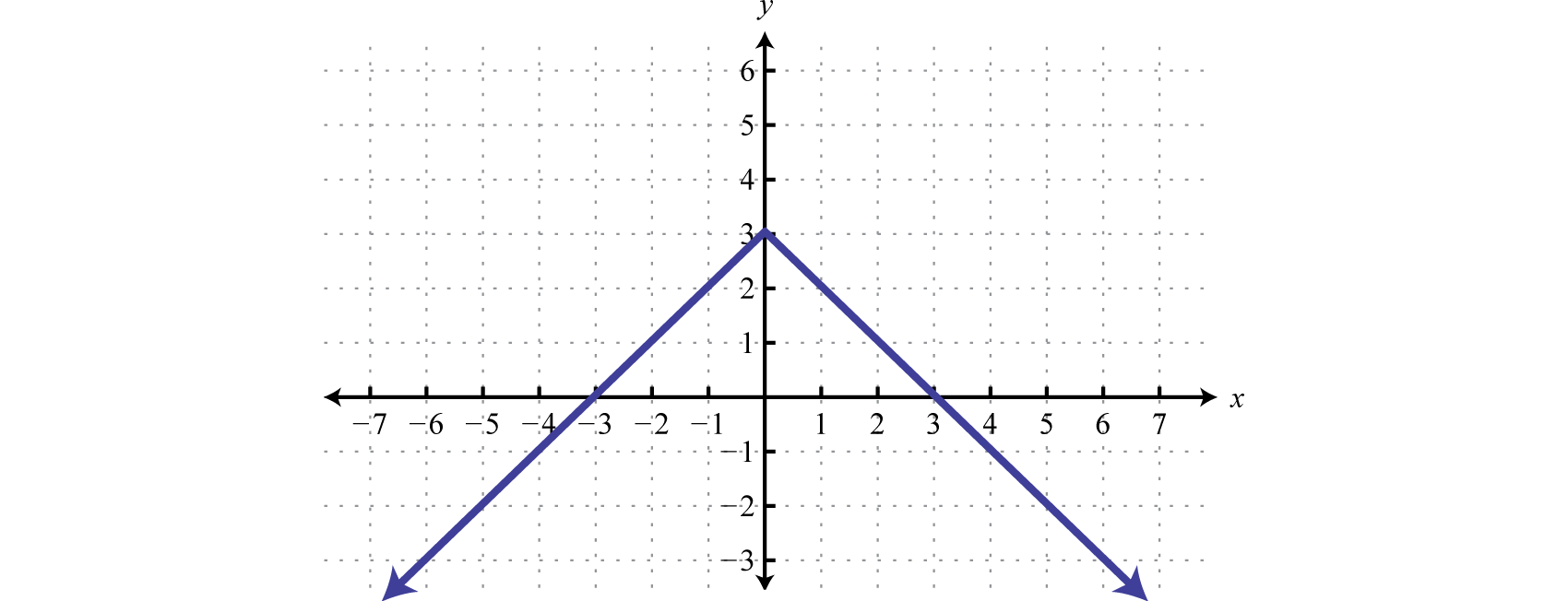
Figura2.5.13 www.youtube.com/v/xsblkfwwzbc
Dilataciones
Las traducciones horizontales y verticales, así como las reflexiones, se denominan transformaciones rígidas porque la forma de la gráfica básica se deja sin cambios, o rígida. Las funciones que se multiplican por un número real distinto de1, dependiendo del número real, parecen estar estiradas verticalmente u horizontalmente. Este tipo de transformación no rígida se denomina dilatación 62. Por ejemplo, podemos multiplicar la función de cuadraturaf(x)=x2 por4 y14 ver qué pasa con la gráfica.

Compare la gráfica deg yh con la función de cuadratura básica definida porf(x)=x2, que se muestra discontinua en gris a continuación:
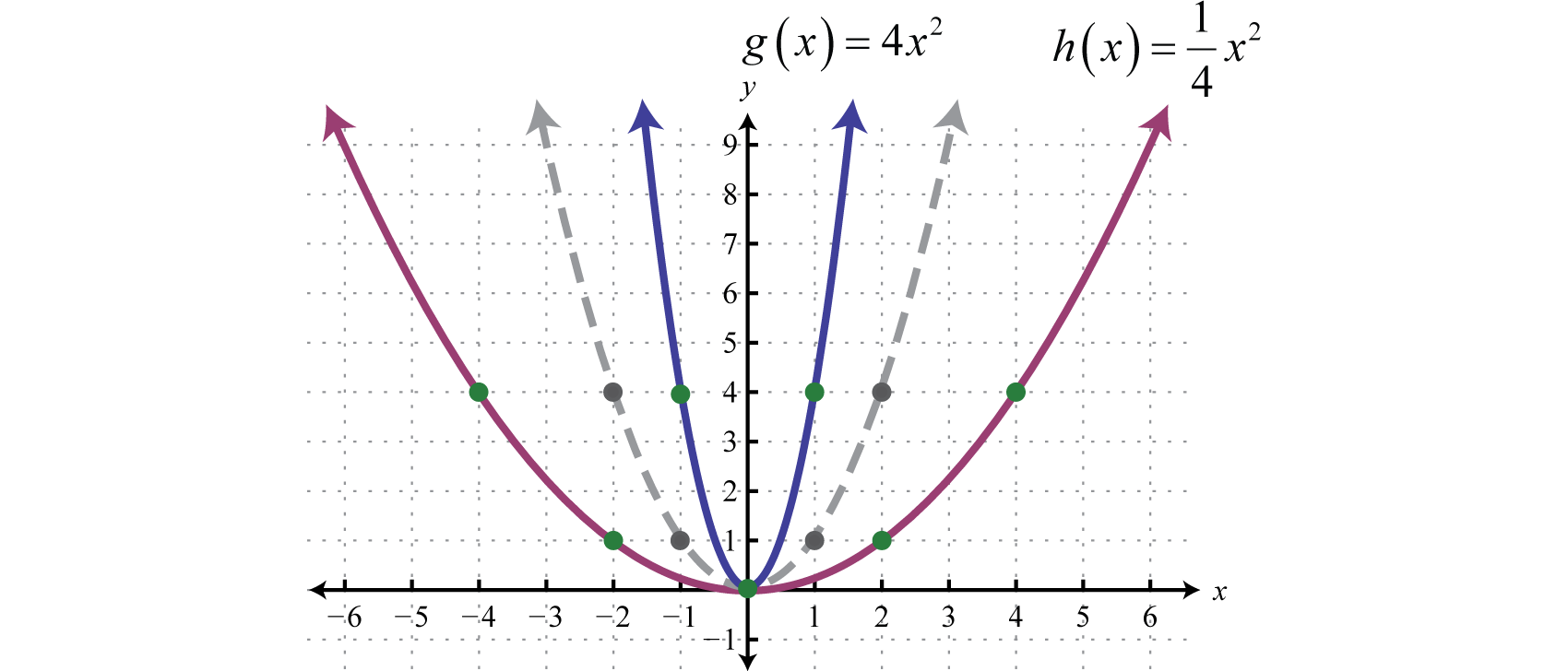
La funcióng es más pronunciada que la función básica de cuadratura y su gráfica parece haberse estirado verticalmente. La función noh es tan empinada como la función básica de cuadratura y parece haberse estirado horizontalmente.
En general, tenemos:
| Dilatación: | F(x)=a⋅f(x) |
|---|
Si el factora es una fracción distinta de cero entre−1 y1, estirará la gráfica horizontalmente. De lo contrario, la gráfica se estirará verticalmente. Si el factora es negativo, entonces también producirá una reflexión.
Ejemplo2.5.6:
Esbozar la gráfica deg(x)=−2|x−5|−3.
Solución
Aquí comenzamos con el producto de−2 y la función de valor absoluto básico:y=−2|x| Esto da como resultado una reflexión y una dilatación.
.png)
Usa los puntos{(−1,−2),(0,0),(1,−2)} para graficar la función reflejada y dilataday=−2|x|. Después traduzca esta gráfica5 unidades a la derecha y3 unidades hacia abajo.
y=−2|x|Basicgraphwithdilationandreflectionaboutthex−axis.y=−2|x−5|Shiftright5units.y=−2|x−5|−3Shiftdown3units.
Respuesta:
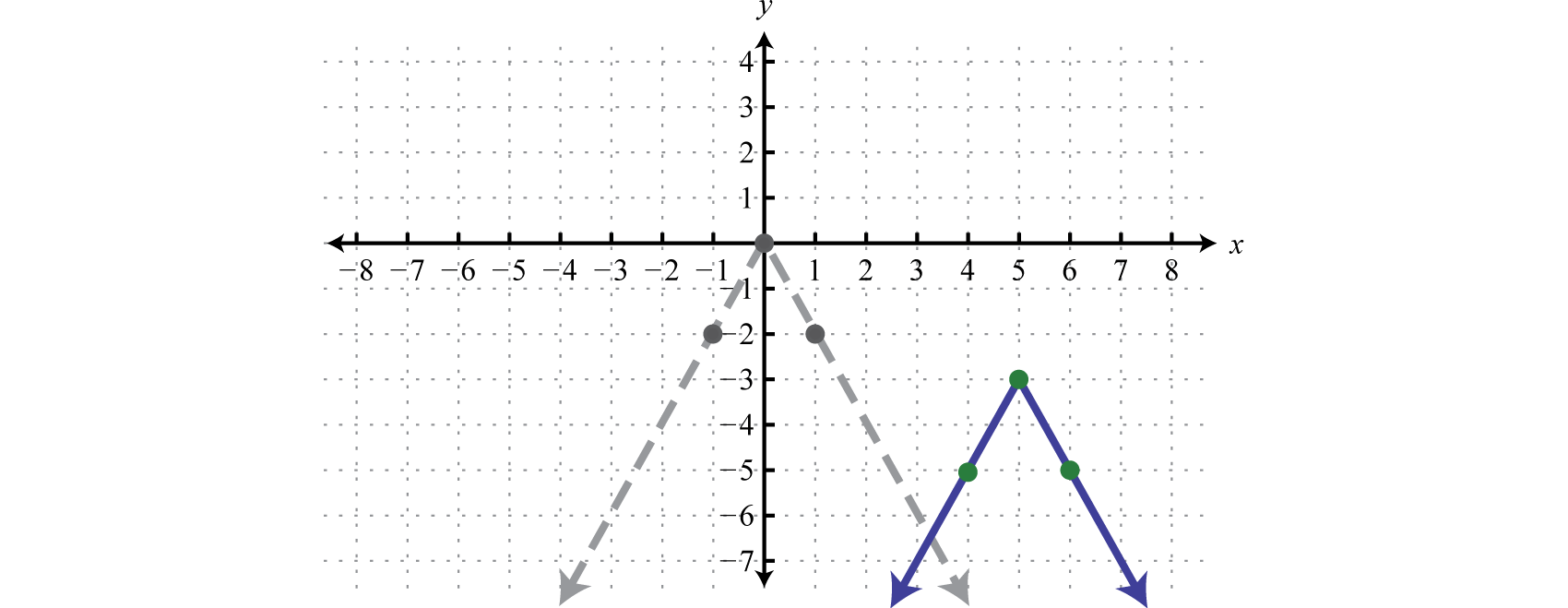
En resumen, dados los números reales positivosh yk:
| kUnidades de cambio vertical hacia arriba: | F(x)=f(x)+k |
|---|---|
| kUnidades de cambio vertical hacia abajo: | F(x)=f(x)−k |
| hUnidades de desplazamiento horizontal a la izquierda: | F(x)=f(x+h) |
|---|---|
| hUnidades de desplazamiento horizontal a la derecha: | F(x)=f(x−h) |
| Reflexión sobre ely eje: | F(x)=f(−x) |
|---|---|
| Reflexión sobre elx eje: | F(x)=−f(x) |
| Dilatación: | F(x)=a⋅f(x) |
|---|
Claves para llevar
- Identificar transformaciones nos permite esbozar rápidamente la gráfica de funciones. Esta habilidad será útil a medida que avancemos en nuestro estudio de las matemáticas. A menudo, una comprensión geométrica de un problema conducirá a una solución más elegante.
- Si se agrega una constante positiva a una función,f(x)+k, la gráfica se desplazará hacia arriba. Si se resta una constante positiva de una función,f(x)−k, la gráfica se desplazará hacia abajo. La forma básica de la gráfica seguirá siendo la misma.
- Si se agrega una constante positiva al valor en el dominio antes de aplicar la función,f(x+h), la gráfica se desplazará hacia la izquierda. Si se resta una constante positiva del valor en el dominio antes de aplicar la funciónf(x−h), la gráfica se desplazará a la derecha. La forma básica seguirá siendo la misma.
- Multiplicando una función por una constante negativa,−f(x), refleja su gráfica en elx eje -eje. Multiplicando los valores en el dominio por−1 antes de aplicar la función,f(−x), refleja la gráfica sobre ely eje -eje.
- Al aplicar múltiples transformaciones, primero aplique reflexiones.
- Multiplicar una función por una constante distinta de1,a⋅f(x), produce una dilatación. Si la constante es un número positivo mayor que1, la gráfica aparecerá estirarse verticalmente. Si la constante positiva es una fracción menor que1, la gráfica aparecerá estirarse horizontalmente.
Ejercicio2.5.3
Haga coincidir la gráfica con la definición de la función.
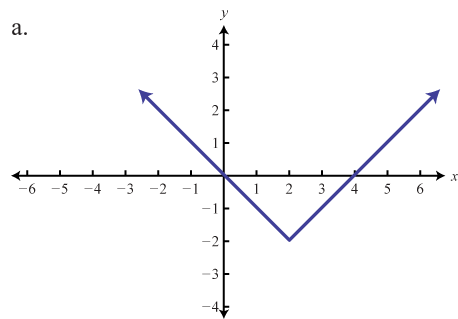
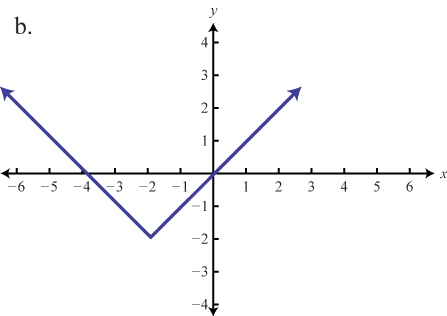
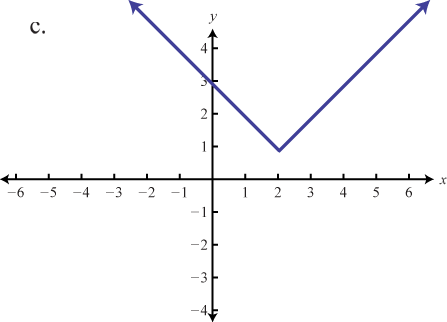
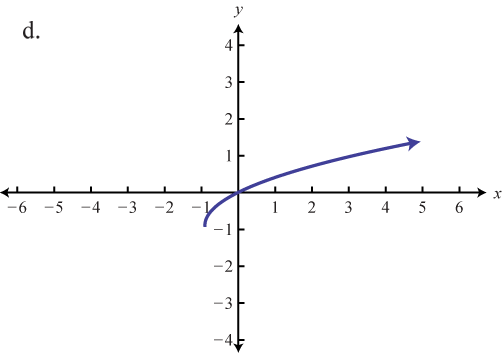
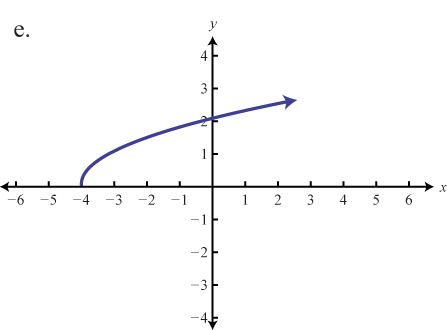
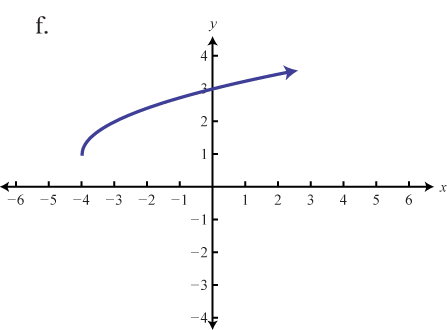
- f(x)=√x+4
- f(x)=|x−2|−2
- f(x)=√x+1−1
- f(x)=|x−2|+1
- f(x)=√x+4+1
- f(x)=|x+2|−2
- Responder
-
1. e
3. d
5. f
Ejercicio2.5.4
Grafica la función dada. Identificar la función básica y las traducciones utilizadas para bosquejar la gráfica. Después, indique el dominio y el rango.
- f(x)=x+3
- f(x)=x−2
- g(x)=x2+1
- g(x)=x2−4
- g(x)=(x−5)2
- g(x)=(x+1)2
- g(x)=(x−5)2+2
- g(x)=(x+2)2−5
- h(x)=|x+4|
- h(x)=|x−4|
- h(x)=|x−1|−3
- h(x)=|x+2|−5
- g(x)=√x−5
- g(x)=√x−5
- g(x)=√x−2+1
- g(x)=√x+2+3
- h(x)=(x−2)3
- h(x)=x3+4
- h(x)=(x−1)3−4
- h(x)=(x+1)3+3
- f(x)=1x−2
- f(x)=1x+3
- f(x)=1x+5
- f(x)=1x−3
- f(x)=1x+1−2
- f(x)=1x−3+3
- g(x)=−4
- g(x)=2
- f(x)=3√x−2+6
- f(x)=3√x+8−4
- Responder
-
1. y=x;3 Unidades de cambio hacia arriba; dominio:R; rango:R
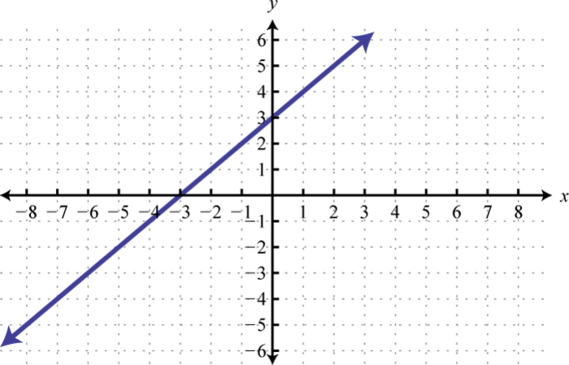
Figura2.5.24 3. y=x2;1 Unidad de cambio hacia arriba; dominio:ℝ; rango:[1,∞)
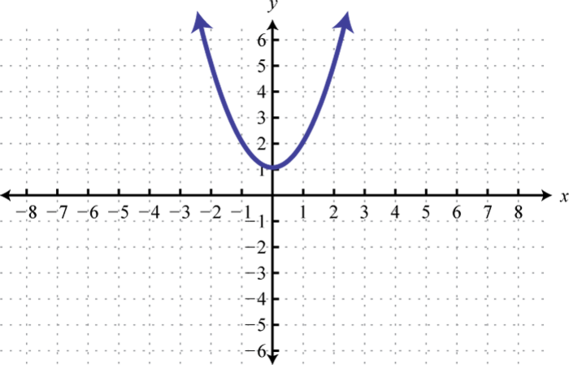
Figura2.5.25 5. y=x2;5 Unidades de desplazamiento a la derecha; dominio:ℝ; rango:[0,∞)
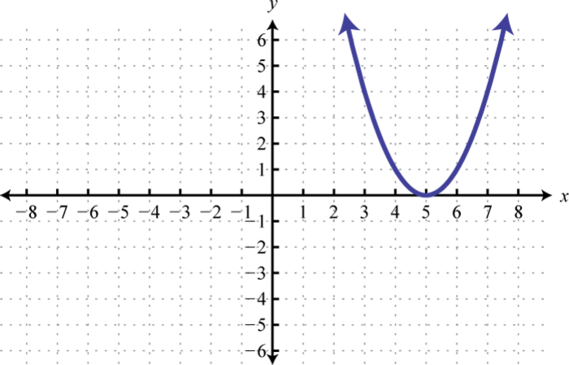
Figura2.5.26 7. y=x2; Desplazar5 unidades a la derecha y2 unidades ascendentes; dominio:ℝ; rango:[2,∞)
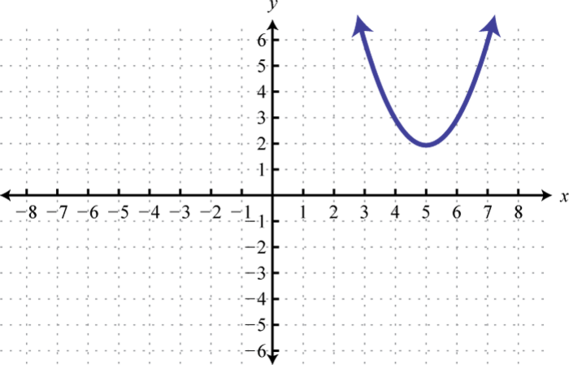
Figura2.5.27 9. y=|x|; Desplazar4 unidades a la izquierda; dominio:ℝ; rango:[0,∞)
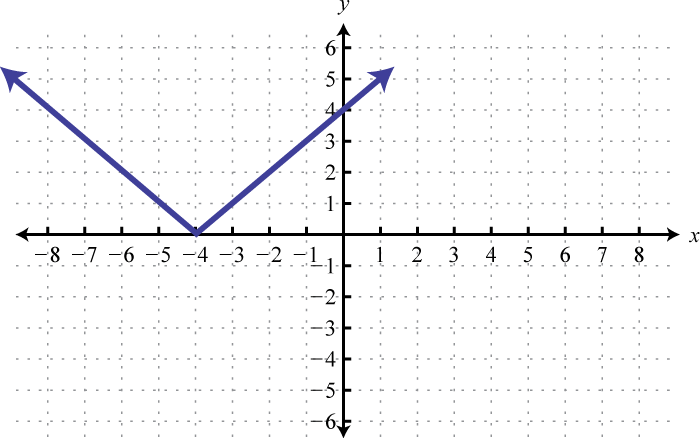
Figura2.5.28 11. y=|x|;1 Unidad de desplazamiento a la derecha y3 unidades descendentes; dominio:ℝ; rango:[−3,∞)
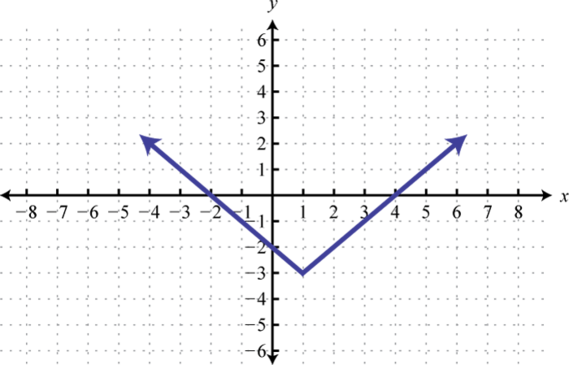
Figura2.5.29 13. y=√x;5 Unidades de desplazamiento hacia abajo; dominio:[0,∞); rango:[−5,∞)
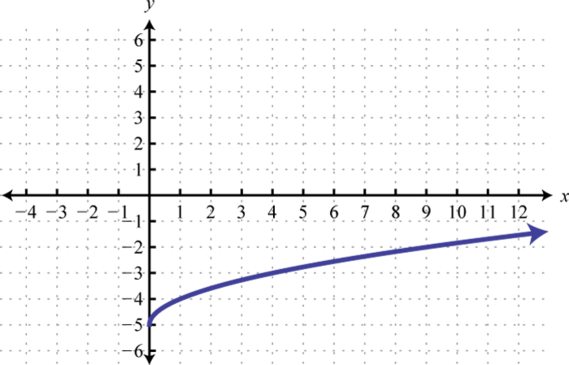
Figura2.5.30 15. y=√x;2 Unidades de desplazamiento a la derecha y1 unidad hacia arriba; dominio:[2,∞); rango:[1,∞)
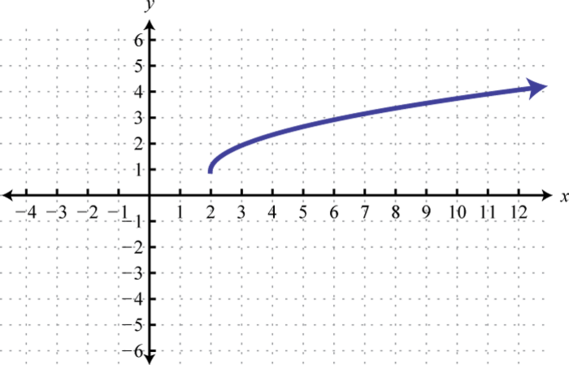
Figura2.5.31 17. y=x3;2 Unidades de desplazamiento a la derecha; dominio:ℝ; rango:ℝ
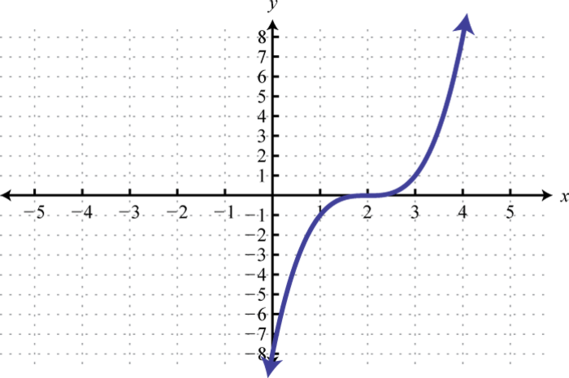
Figura2.5.32 19. y=x3;1 Unidad de desplazamiento a la derecha y4 unidades descendentes; dominio:ℝ; rango:ℝ
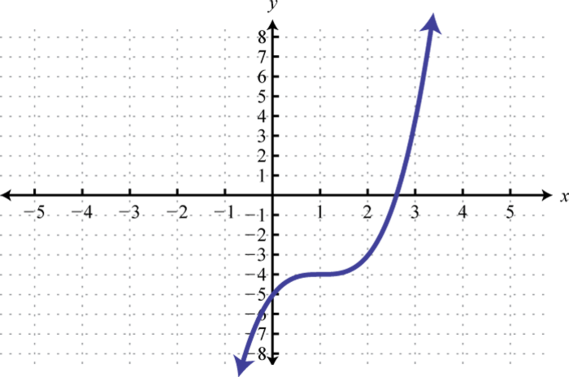
Figura2.5.33 21. y=1x;2 Unidades de desplazamiento a la derecha; dominio:(−∞,2)∪(2,∞); rango:(−∞,0)∪(0,∞)
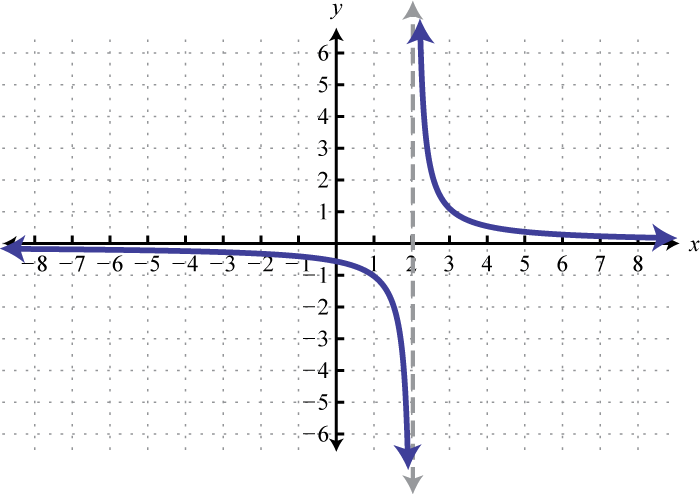
Figura2.5.34 23. y=1x;5 Unidades de cambio hacia arriba; dominio:(−∞,0)∪(0,∞); rango:(−∞,1)∪(1,∞)
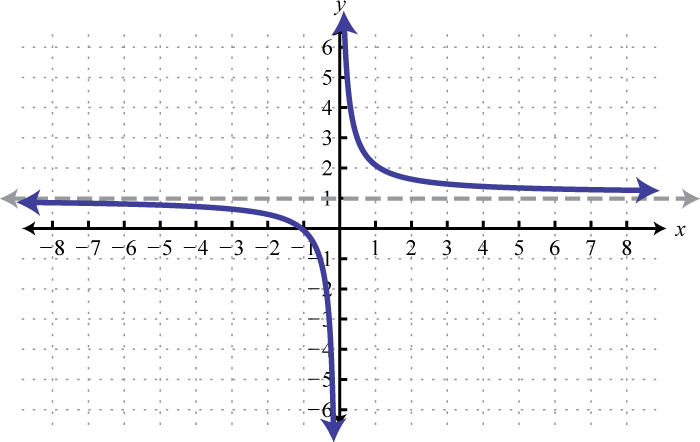
Figura2.5.35 25. y=1x;1 Unidad de desplazamiento a la izquierda y2 unidades descendentes; dominio:(−∞,−1)∪(−1,∞); rango:(−∞,−2)∪(−2,∞)
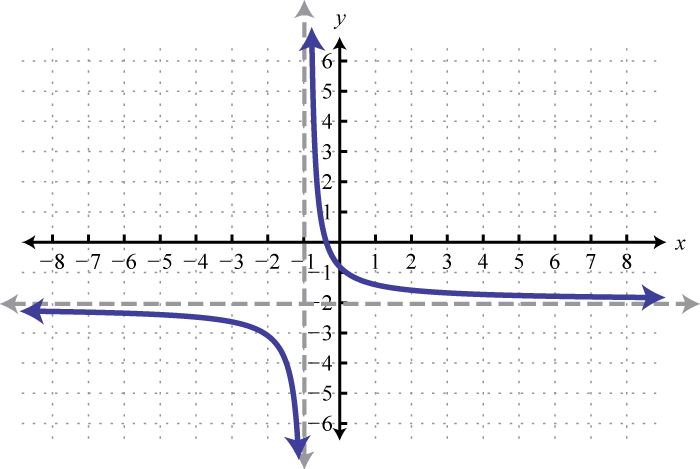
Figura2.5.36 27. Gráfica básicay=−4; dominio:ℝ; rango:{−4}

Figura2.5.37 29. y=3√x;6 Unidades de desplazamiento hacia arriba y2 unidades derechas; dominio:ℝ; rango:ℝ
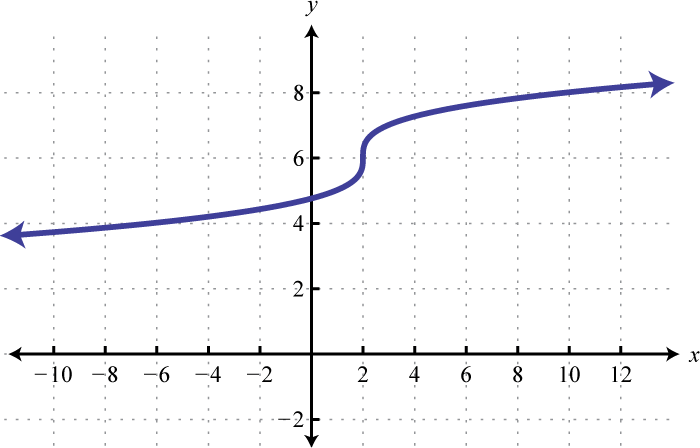
Figura2.5.38
Ejercicio2.5.5
Grafica las funciones por partes.
- h(x)={x2+2 if x<0x+2 if x≥0
- h(x)={x2−3 if x<0√x−3 if x≥0
- h(x)={x3−1 if x<0|x−3|−4 if x≥0
- h(x)={x3 if x<0(x−1)2−1 if x≥0
- h(x)={x2−1 if x<02 if x≥0
- h(x)={x+2 if x<0(x−2)2 if x≥0
- h(x)={(x+10)2−4 if x<−8x+4 if −8≤x<−4√x+4 if x≥−4
- f(x)={x+10 if x≤−10|x−5|−15 if −10<x≤2010 if x>20
- Responder
-
1.
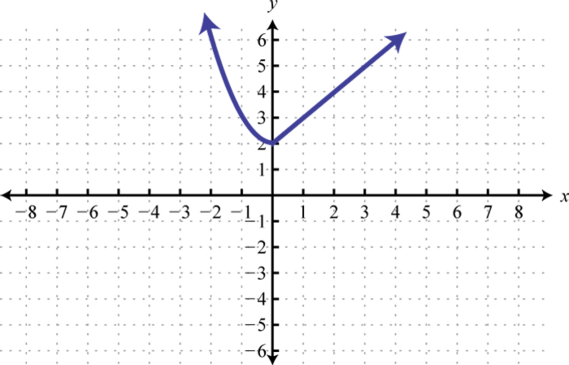
Figura2.5.39 3.
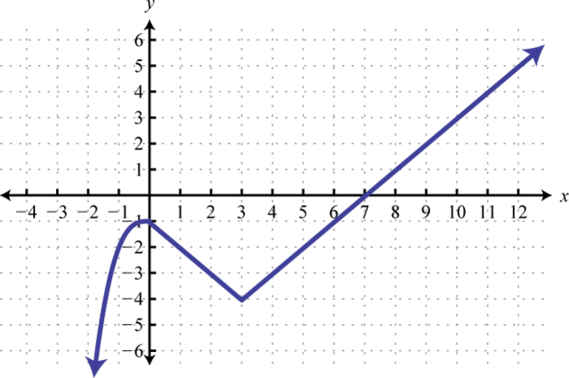
Figura2.5.40 5.
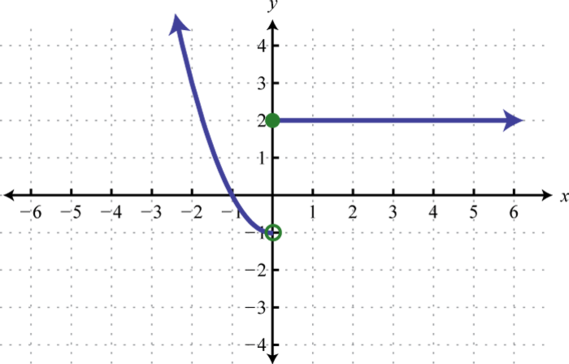
Figura2.5.41 7.
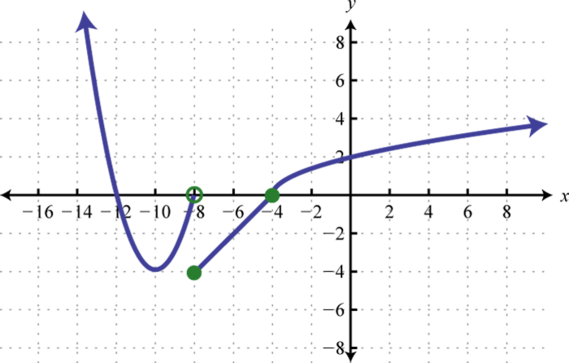
Figura2.5.42
Ejercicio2.5.6
Escribe una ecuación que represente la función cuya gráfica se da.
1.
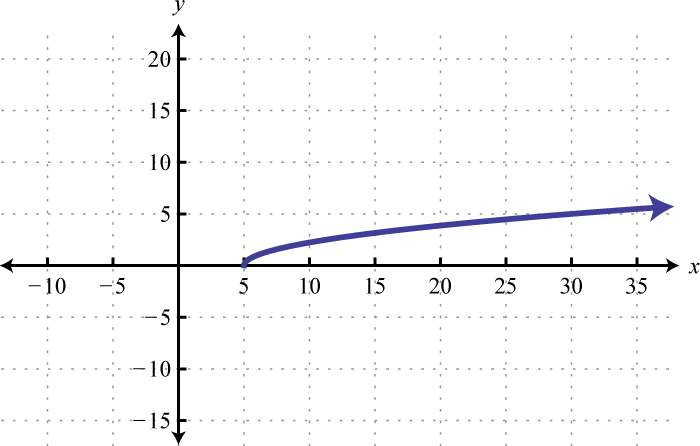
2.
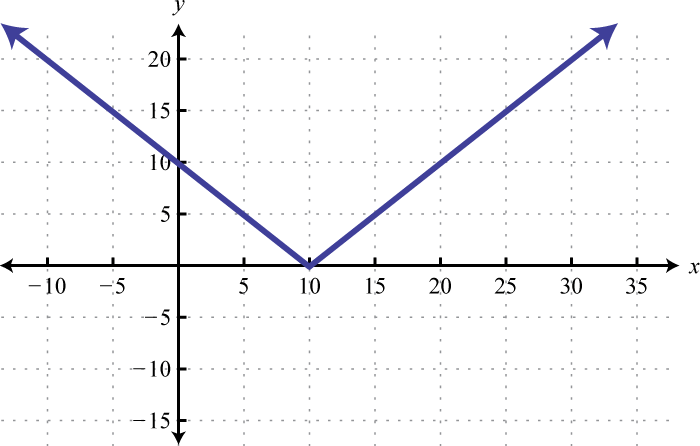
3.
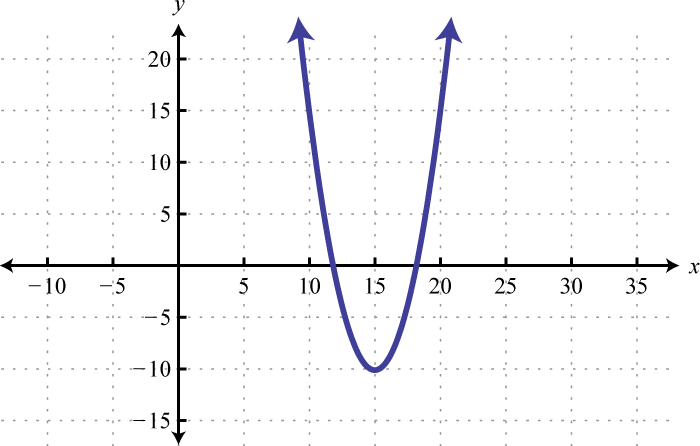
4.
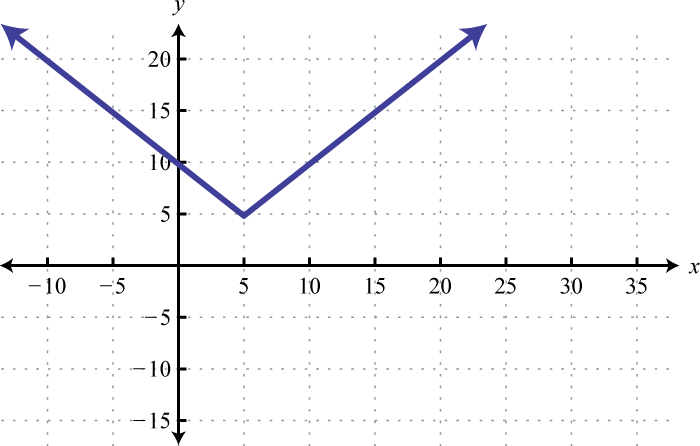
5.
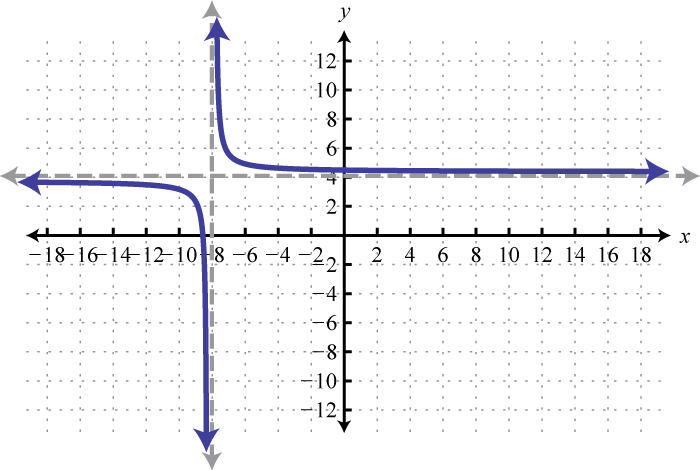
6.
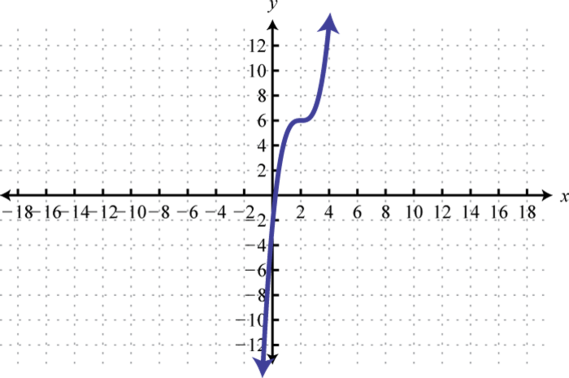
7.
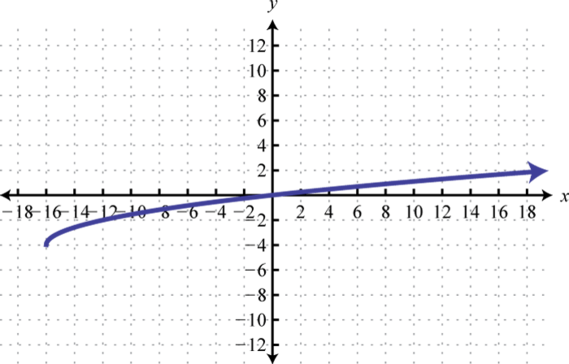
8.
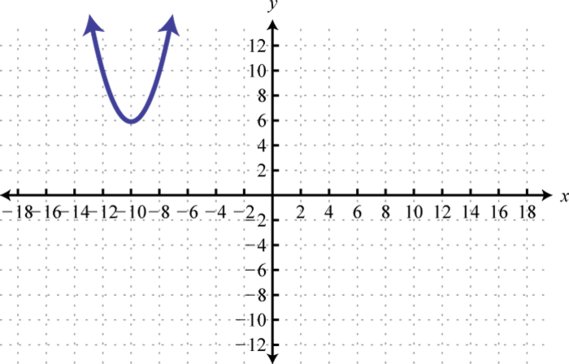
- Responder
-
1. f(x)=√x−5
3. f(x)=(x−15)2−10
5. f(x)=1x+8+4
7. f(x)=√x+16−4
Ejercicio2.5.6
Haga coincidir la gráfica con la definición de función dada.
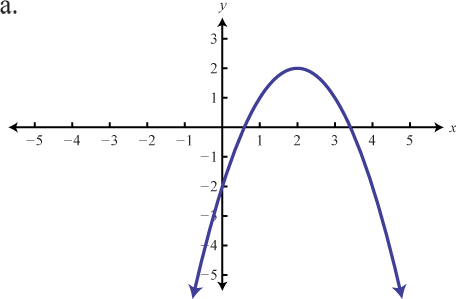

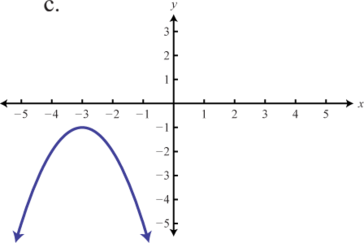
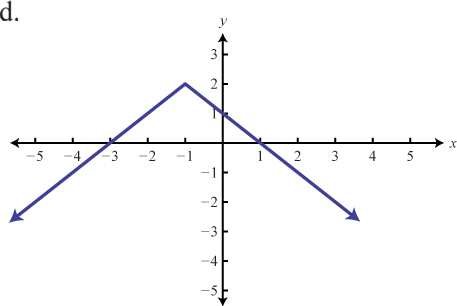
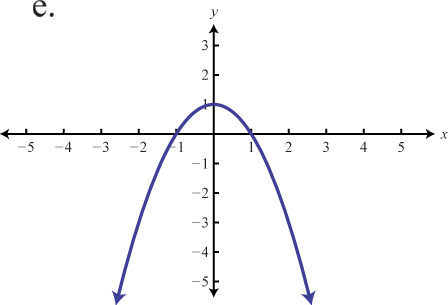
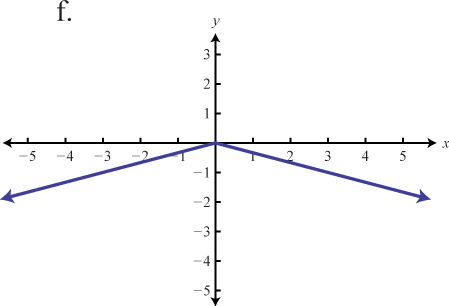
- f(x)=−3|x|
- f(x)=−(x+3)2−1
- f(x)=−|x+1|+2
- f(x)=−x2+1
- f(x)=−13|x|
- f(x)=−(x−2)2+2
- Responder
-
1. b
3. d
5. f
Ejercicio2.5.7
Utilice las transformaciones para graficar las siguientes funciones.
- f(x)=−x+5
- f(x)=−|x|−3
- g(x)=−|x−1|
- f(x)=−(x+2)2
- h(x)=√−x+2
- g(x)=−√x+2
- g(x)=−(x+2)3
- h(x)=−√x−2+1
- g(x)=−x3+4
- f(x)=−x2+6
- f(x)=−3|x|
- g(x)=−2x2
- h(x)=12(x−1)2
- h(x)=13(x+2)2
- g(x)=−12√x−3
- f(x)=−5√x+2
- f(x)=4√x−1+2
- h(x)=−2x+1
- g(x)=−14(x+3)3−1
- f(x)=−5(x−3)2+3
- h(x)=−3|x+4|−2
- f(x)=−1x
- f(x)=−1x+2
- f(x)=−1x+1+2
- Responder
-
1.
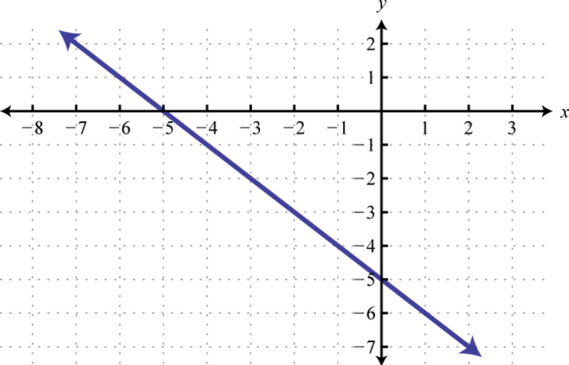
Figura2.5.57 3.
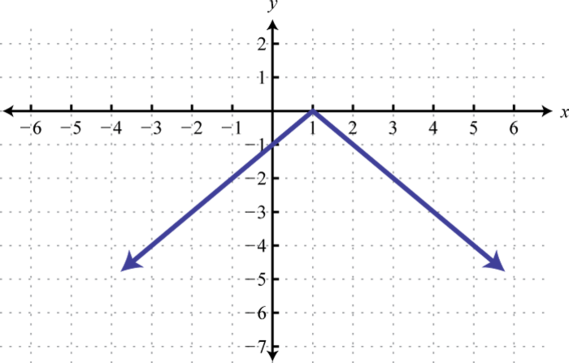
Figura2.5.58 5.
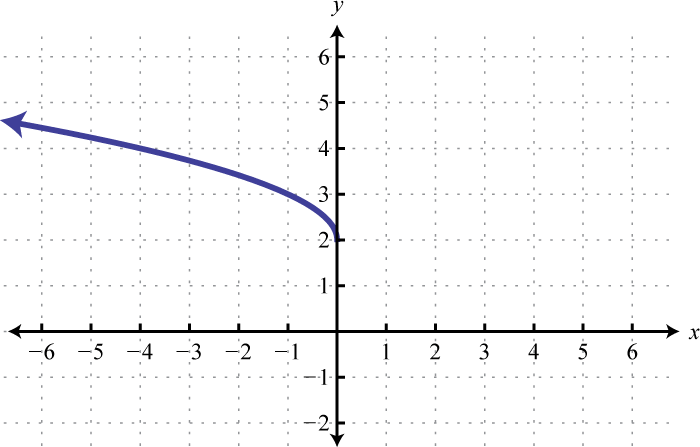
Figura2.5.59 7.
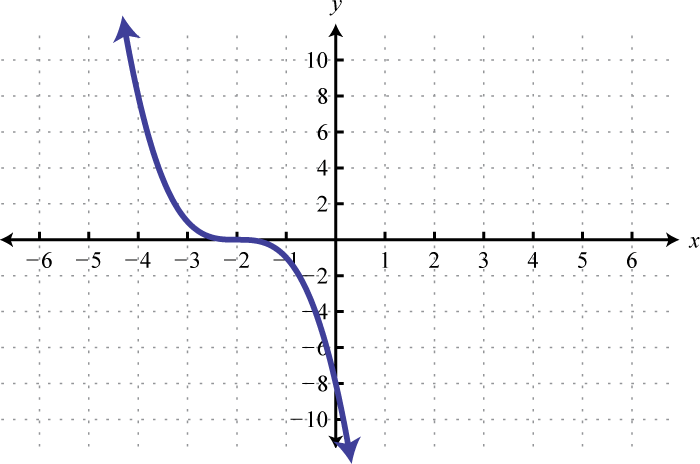
Figura2.5.60 9.
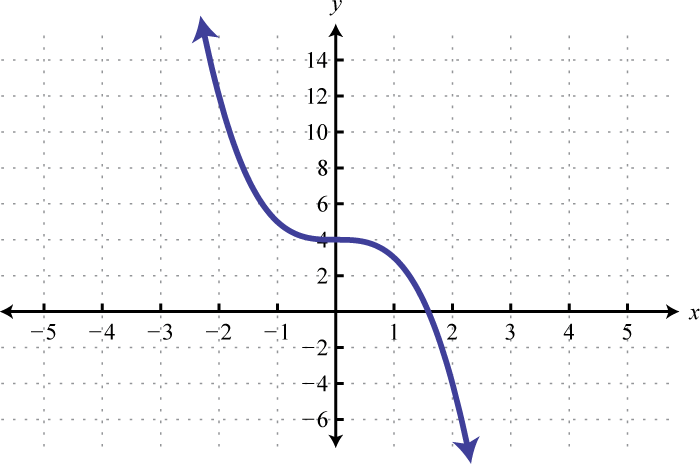
Figura2.5.61 11.
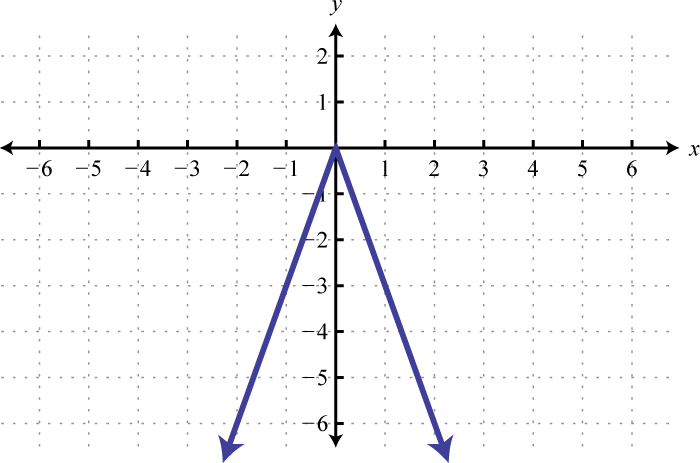
Figura2.5.62 13.
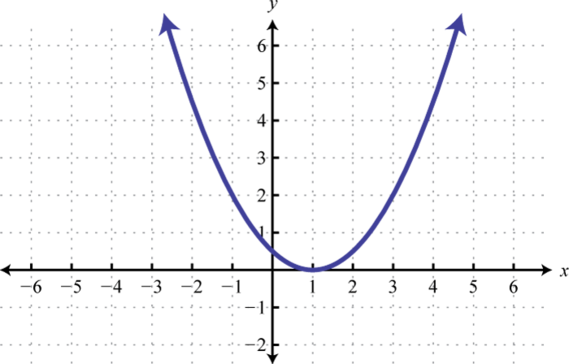
Figura2.5.63 15.
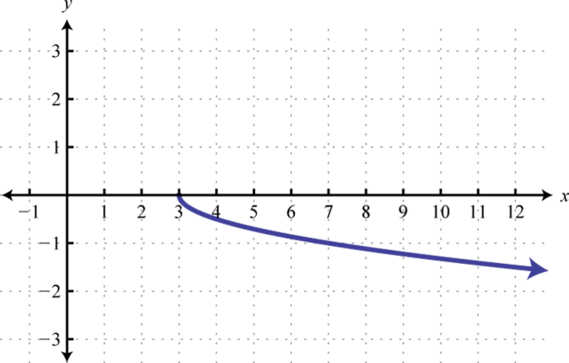
Figura2.5.64 17.
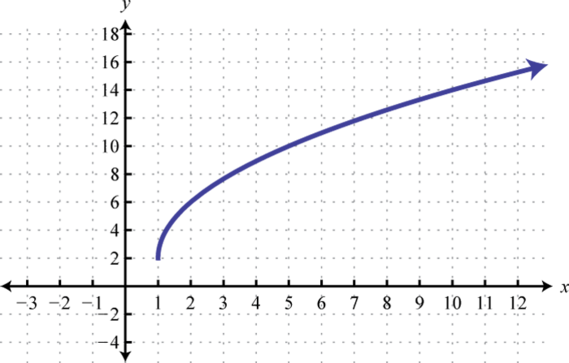
Figura2.5.65 19.
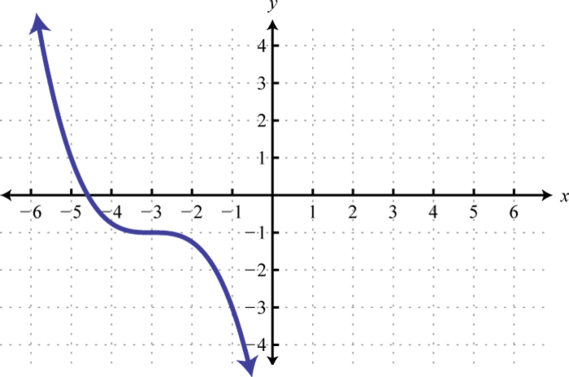
Figura2.5.66 21.
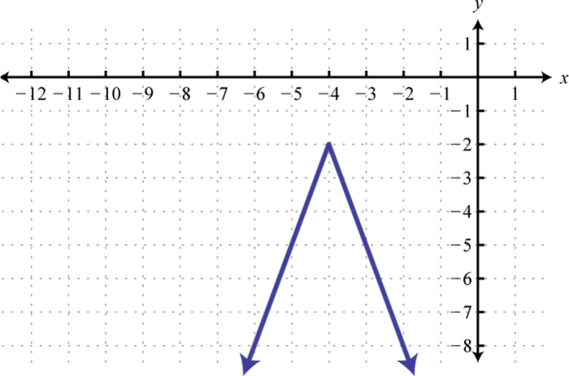
Figura2.5.67 23.
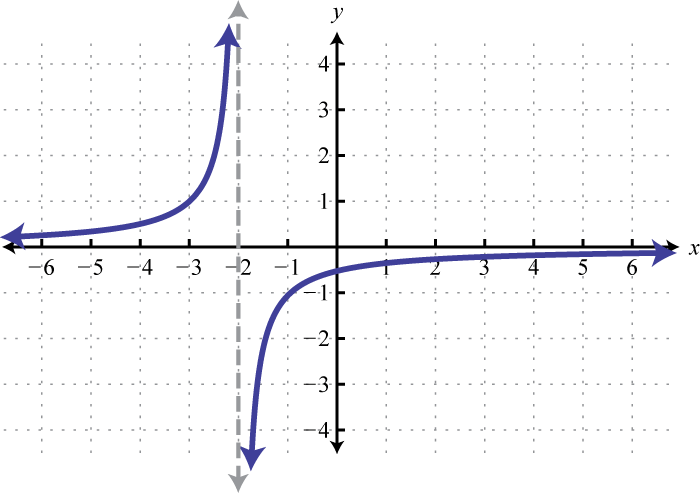
Figura2.5.68
Ejercicio2.5.8
- Utilice diferentes colores para graficar la familia de gráficas definidas pory=kx2, dondek∈{1,12,13,14}. ¿Qué pasa con la gráfica cuando el denominador dek es muy grande? Comparta sus hallazgos en el panel de discusión.
- Gráficaf(x)=√x yg(x)=−√x en el mismo conjunto de ejes de coordenadas. ¿Qué aspecto tiene la forma general? Intenta encontrar una sola ecuación que describa la forma. Comparte tus hallazgos.
- Explora lo que sucede con la gráfica de una función cuando los valores de dominio se multiplican por un factora antes de que se aplique la función,f(ax). Elaborar algunas reglas para esta situación y compartirlas en el panel de discusión.
- Responder
-
1. La respuesta puede variar
3. La respuesta puede variar
Notas al pie
57 Un conjunto de operaciones que cambian la ubicación de una gráfica en un plano de coordenadas pero dejan el tamaño y la forma sin cambios.
58 Un conjunto de operaciones que cambian el tamaño y/o la forma de una gráfica en un plano de coordenadas.
59 Una transformación rígida que desplaza una gráfica hacia arriba o hacia abajo.
60 Una transformación rígida que desplaza una gráfica hacia la izquierda o hacia la derecha.
61 Una transformación que produce una imagen especular de la gráfica alrededor de un eje.
62 Una transformación no rígida, producida multiplicando funciones por un número real distinto de cero, que parece estirar la gráfica vertical u horizontalmente.


