2.4: Graficando las Funciones Básicas
( \newcommand{\kernel}{\mathrm{null}\,}\)
Objetivos de aprendizaje
- Definir y graficar siete funciones básicas.
- Definir y graficar funciones por tramos.
- Evaluar funciones definidas por tramos.
- Define la mayor función entera.
Funciones Básicas
En esta sección graficamos siete funciones básicas que serán utilizadas a lo largo de este curso. Cada función se grafica trazando puntos. Recuerda esof(x)=y y asíf(x) y sey puede usar indistintamente.
Cualquier función de la formaf(x)=c, dondec está cualquier número real, se llama una función constante 43. Las funciones constantes son lineales y se pueden escribirf(x)=0x+c. En esta forma, es claro que la pendiente es0 y lay -intercepción es(0,c). Evaluar cualquier valor parax, comox=2, resultará enc.

La gráfica de una función constante es una línea horizontal. El dominio consta de todos los números realesℝ y el rango consiste en el valor único{c}.
A continuación definimos la función de identidad 44f(x)=x. Evaluar cualquier valor parax resultará en ese mismo valor. Por ejemplo,f(0)=0 yf(2)=2. La función de identidad es linealf(x)=1x+0,, con pendientem=1 ey -intercepción(0,0).
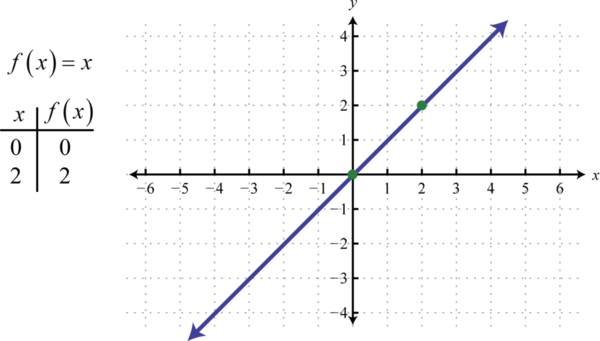
Tanto el dominio como el rango constan de todos los números reales.
La función de cuadratura 45, definida porf(x)=x2, es la función obtenida al cuadrar los valores en el dominio. Por ejemplo,f(2)=(2)2=4 yf(−2)=(−2)2=4 .El resultado de cuadrar valores distintos de cero en el dominio siempre será positivo.
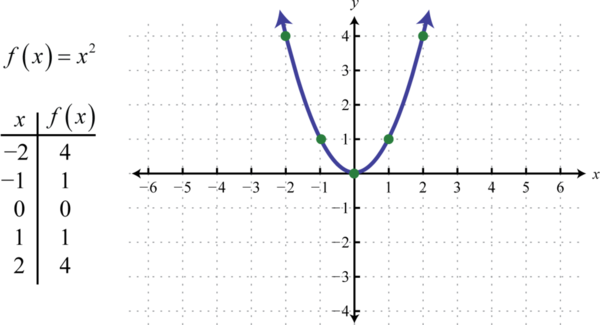
El gráfico curvo resultante se llama parábola 46. El dominio consta de todos los números realesℝ y el rango consiste en todosy los -valores mayores o iguales a cero[0,∞).
La función de cubicación 47, definida porf(x)=x3, eleva todos los valores en el dominio a la tercera potencia. Los resultados pueden ser positivos, cero o negativos. Por ejemplo,f(1)=(1)3=1,f(0)=(0)3=0, yf(−1)=(−1)3=−1.
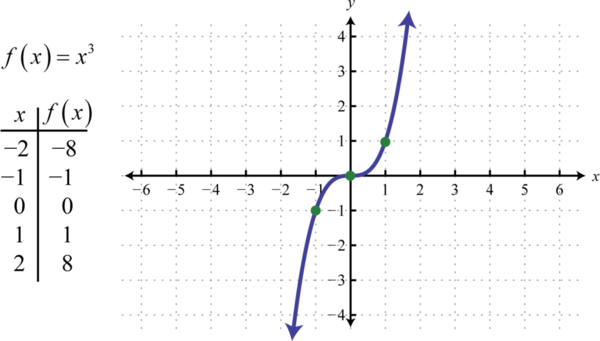
Tanto el dominio como el rango constan de todos los números realesℝ.
Tenga en cuenta que las funciones de constante, identidad, cuadratura y cubicación son ejemplos de funciones polinómicas básicas. Las siguientes tres funciones básicas no son polinomios.
La función de valor absoluto 48, definida porf(x)=|x|, es una función donde la salida representa la distancia al origen en una recta numérica. El resultado de evaluar la función de valor absoluto para cualquier valor distinto de cero de siemprex será positivo. Por ejemplo,f(−2)=|−2|=2 yf(2)=|2|=2.
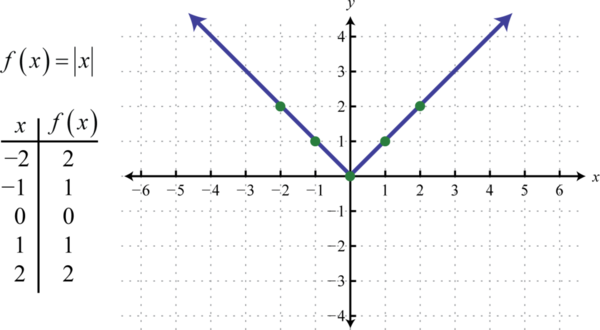
El dominio de la función de valor absoluto consiste en todos los números realesℝ y el rango consiste en todosy los -valores mayores o iguales a cero[0,∞).
La función 49 de raíz cuadrada, definida porf(x)=√x, no se define como un número real si losx valores -son negativos. Por lo tanto, el valor más pequeño en el dominio es cero. Por ejemplo,f(0)=√0=0 yf(4)=√4=2.
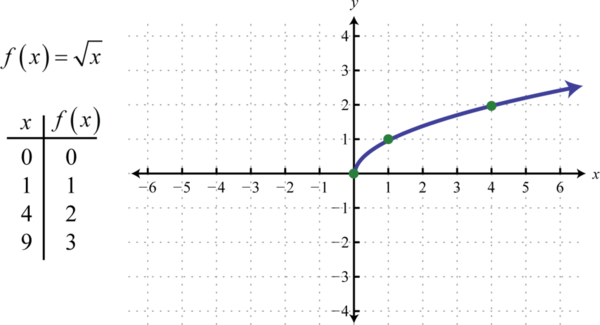
Tanto el dominio como el rango consisten en números reales mayores o iguales a cero[0,∞).
La función recíproca 50, definida porf(x)=1x, es una función racional con una restricción en el dominio, a saberx≠0. El recíproco de unx -valor muy cercano a cero es muy grande. Por ejemplo,
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1,000)=1(11,000)=1⋅1,0001=1,000
En otras palabras, a medida que losx -valores se acercan a cero, sus recíprocos tenderán hacia el infinito ya sea positivo o negativo. Esto describe una asíntota vertical 51 en ely eje -eje. Además, donde losx valores -son muy grandes el resultado de la función recíproca es muy pequeño.
f(10)=110=0.1f(100)=1100=0.01f(1000)=11,000=0.001
En otras palabras, a medida que losx valores -se vuelven muy grandes,y los valores -resultantes tienden hacia cero. Esto describe una asíntota horizontal 52 en elx eje -eje. Después de trazar una serie de puntos se puede determinar la forma general de la función recíproca.
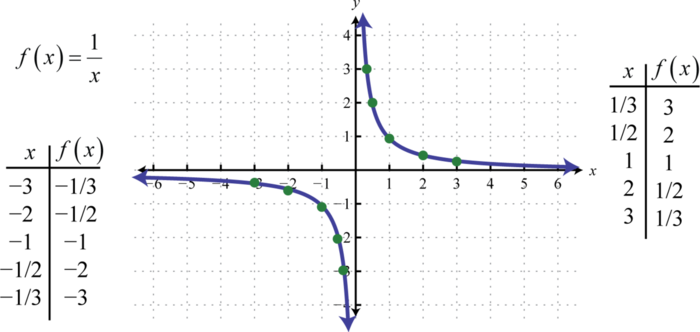
Tanto el dominio como el rango de la función recíproca consisten en todos los números reales excepto0, los cuales se pueden expresar usando la notación de intervalo de la siguiente manera:(−∞,0)∪(0,∞).
En resumen, las funciones polinómicas básicas son:
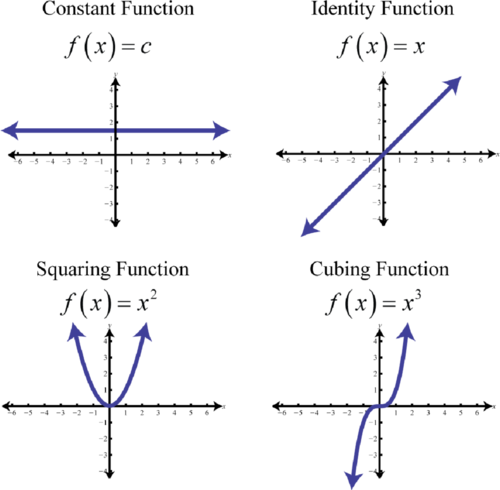
Figura2.4.8
Las funciones básicas no polinómicas son:
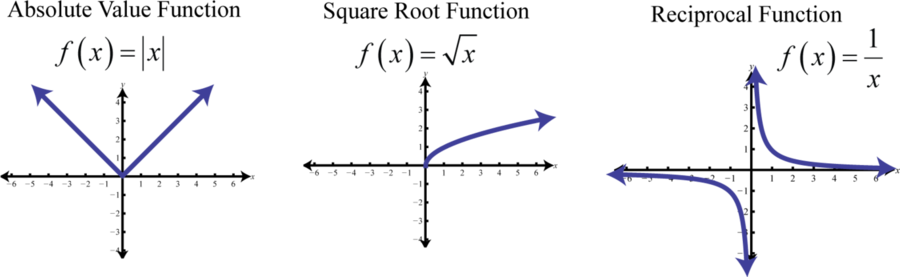
Funciones definidas por piezas
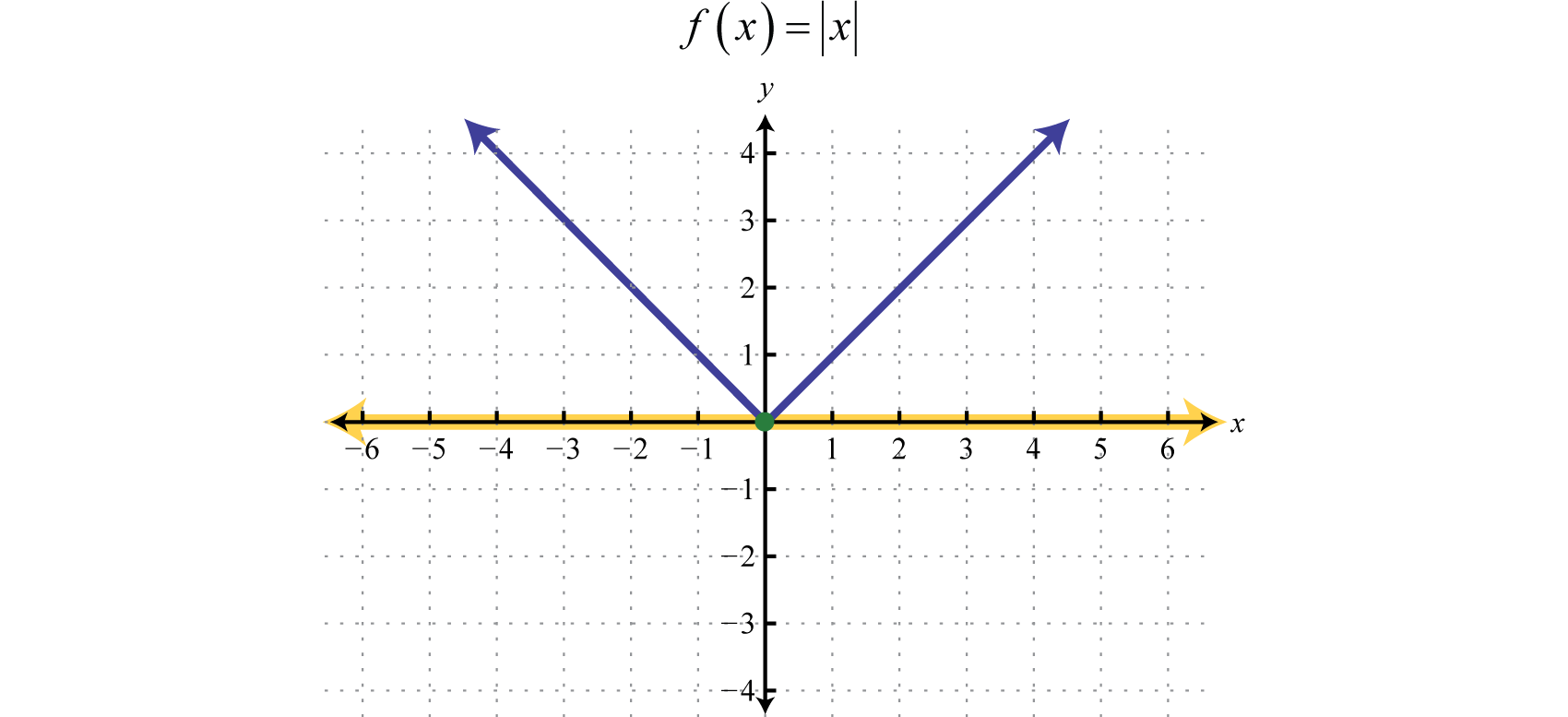
Una función 53 por tramos, o función dividida 54, es una función cuya definición cambia dependiendo del valor en el dominio. Por ejemplo, podemos escribir la función de valor absolutof(x)=|x| como una función por partes:
f(x)=|x|={x if x≥0−x if x<0
En este caso, la definición utilizada depende del signo delx -valor. Si elx -valor es positivox≥0, entonces la función es definida porf(x)=x. Y si elx -valor es negativo,x<0, entonces la función es definida porf(x)=−x.

A continuación se muestra la gráfica de las dos piezas en el mismo plano de coordenadas rectangulares:
Ejemplo2.4.1:
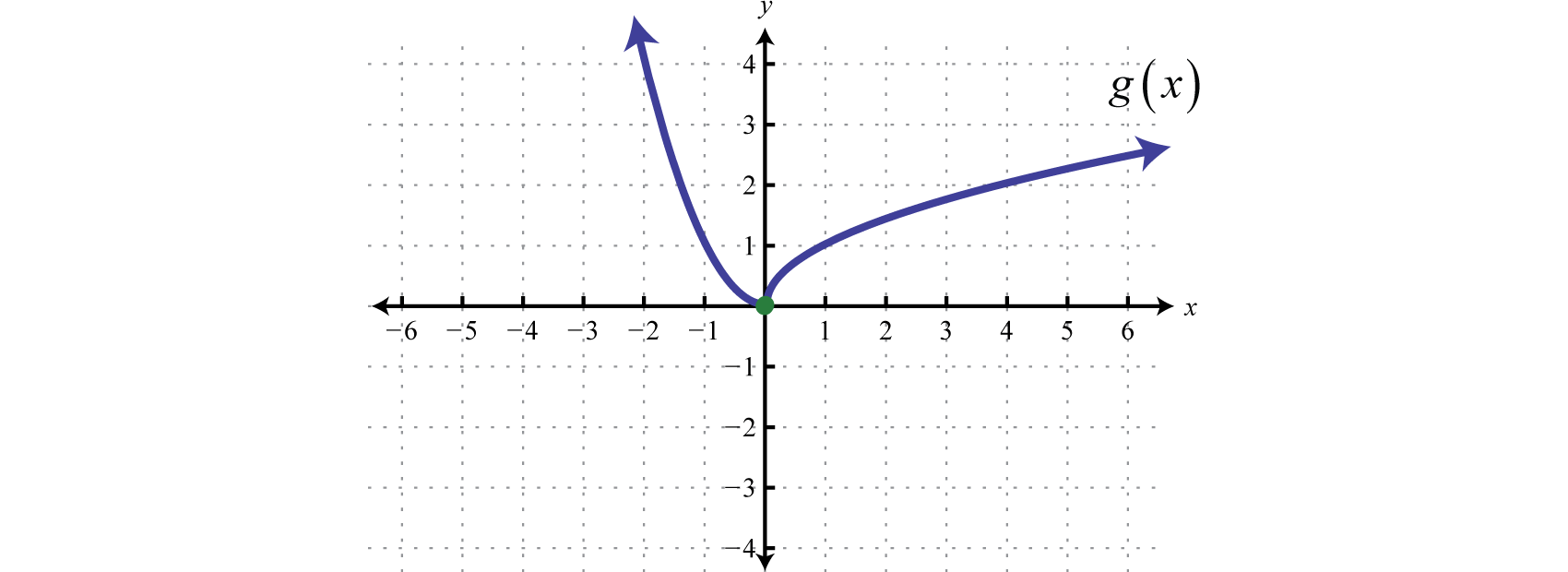
Gráfica:g(x)={x2 if x<0√x if x≥0.
Solución
En este caso, graficamos la función de cuadratura sobrex valores negativos y la función raíz cuadrada sobrex valores positivos.

Observe el punto abierto utilizado en el origen para la función de cuadratura y el punto cerrado utilizado para la función de raíz cuadrada. Esto estuvo determinado por la desigualdad que define el dominio de cada pieza de la función. Toda la función consiste en cada pieza graficada en el mismo plano de coordenadas.
Respuesta:
Al evaluar, el valor en el dominio determina la definición apropiada a utilizar.
Ejemplo2.4.2:
Dada la funciónh, encontrarh(−5),h(0), yh(3).
Solución
Usarh(t)=7t+3 dondet sea negativo, como lo indicat<0.
h(t)=7t+5h(−5)=7(−5)+3=−35+3=−32
Dondet sea mayor o igual a cero, useh(t)=−16t2+32t.
h(0)=−16(0)+32(0)h(3)=16(3)2+32(3)=0+0=−144+96=0=−48
Respuesta:
h(−5)=−32,h(0)=0,yh(3)=−48
Ejercicio2.4.1
Gráfica:f(x)={23x+1 if x<0x2 if x≥0.
- Contestar
-
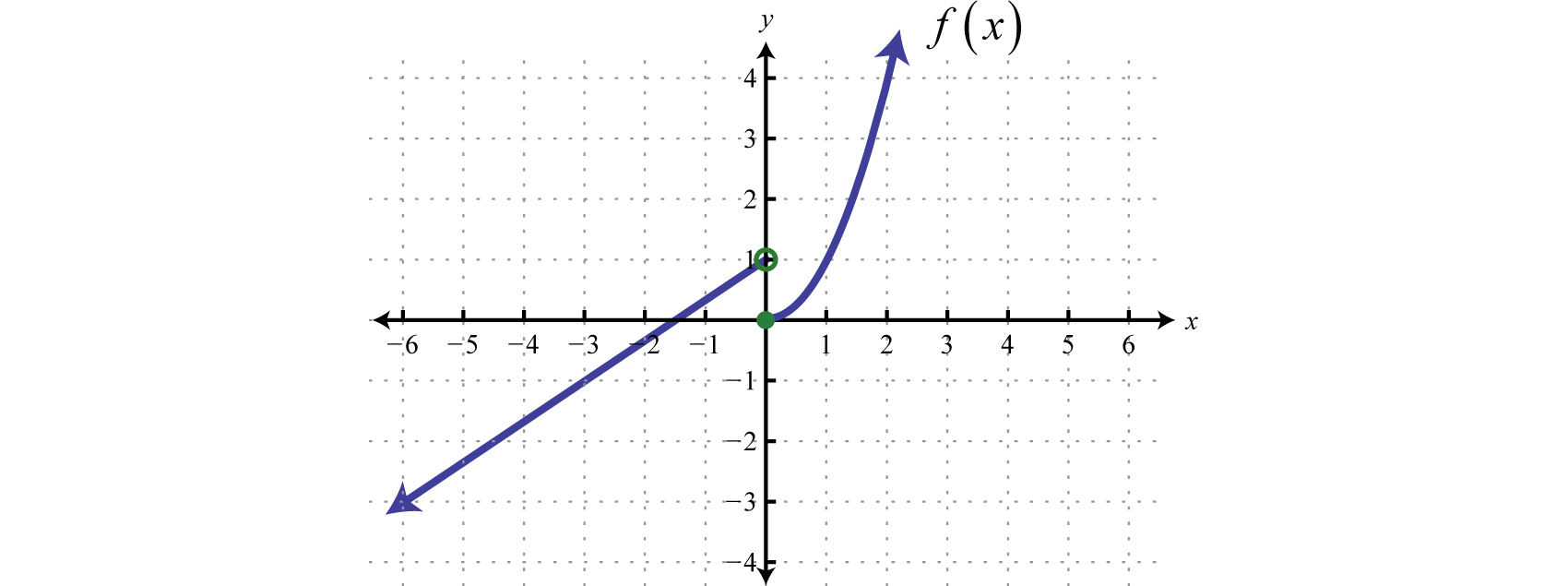
Figura2.4.14 www.youtube.com/v/0Heunsn5BLW
La definición de una función puede ser diferente a lo largo de múltiples intervalos en el dominio.
Ejemplo2.4.3:
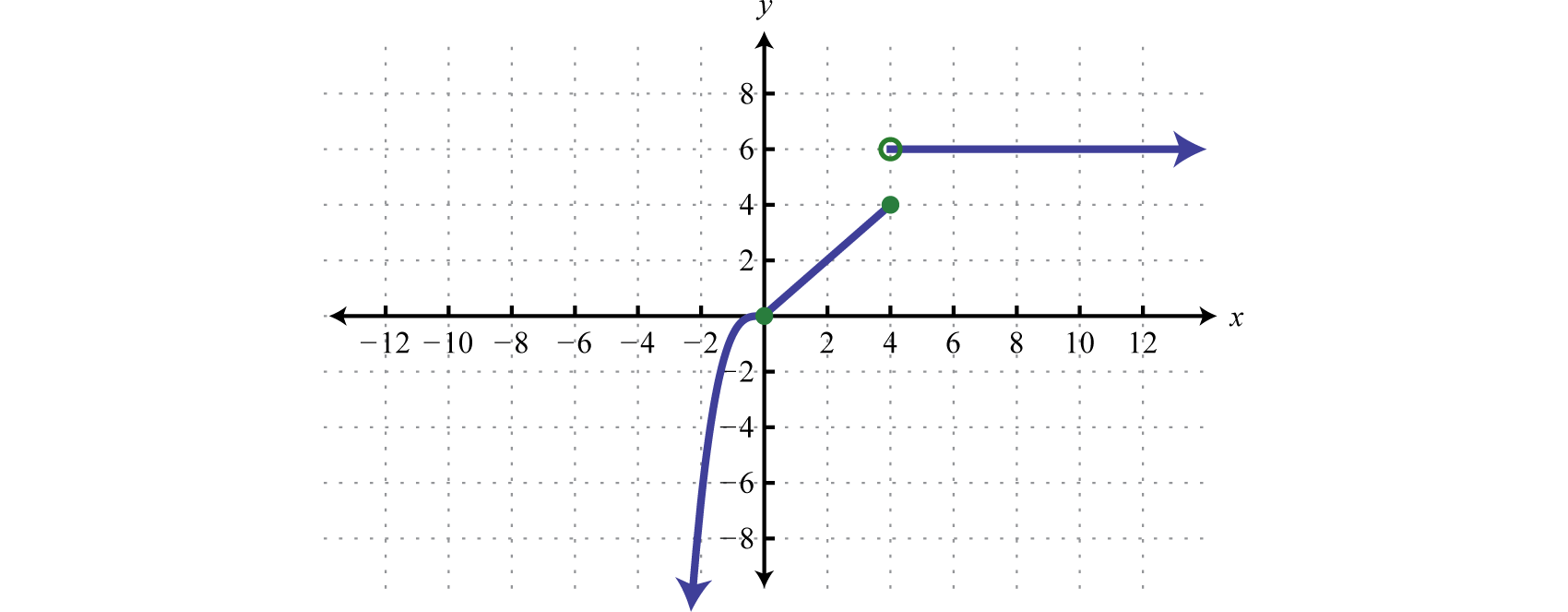
Gráfica:f(x)={x3 if x<0x if 0≤x≤46 if x>4.
Solución
En este caso, grafica la función de cubo a lo largo del intervalo(−∞,0). Grafique la función de identidad a lo largo del intervalo[0,4]. Finalmente, grafica la función constantef(x)=6 a lo largo del intervalo(4,∞). Y porquef(x)=6 dondex>4, usamos un punto abierto en el punto(4,6). Dondex=4, usamosf(x)=x y así(4,4) es un punto en la gráfica como lo indica un punto cerrado.
Respuesta:
La mayor función entera 55, denotadaf(x)=[[x]], asigna el mayor número entero menor o igual a cualquier número real en su dominio. Por ejemplo,
f(2.7)=[[2.7]]=2f(π)=[[π]]=3f(0.23)=[[0.23]]=0f(−3.5)=[[−3.5]]=−4
Esta función asocia cualquier número real con el mayor número entero menor o igual a él y no debe confundirse con redondeo.
Ejemplo2.4.4:
Gráfica:f(x)=[[x]].
Solución
Six es algún número real, entoncesy=[[x]] es el mayor número entero menor o igual ax.
⋮−1≤x<0⇒y=[[x]]=−10≤x<1⇒y=[[x]]=01≤x<2⇒y=[[x]]=1⋮
Usando esto, obtenemos la siguiente gráfica.
Respuesta:
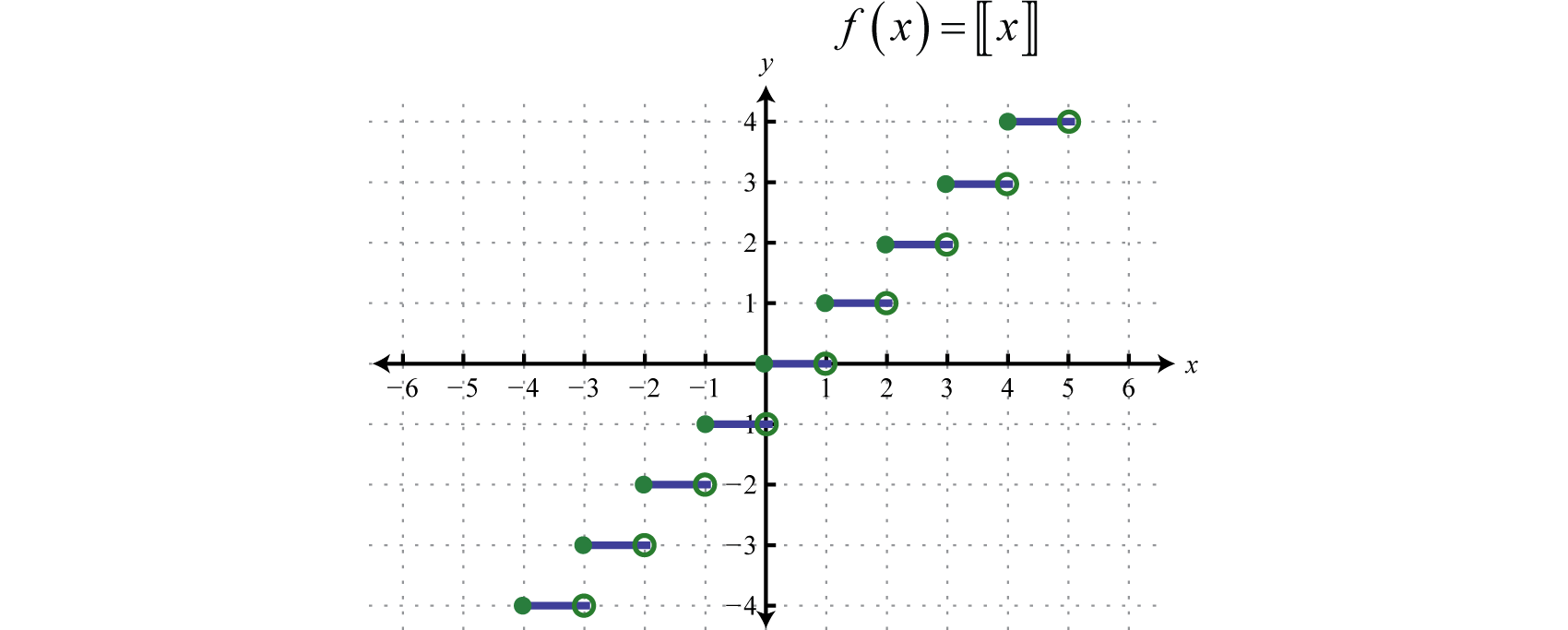
El dominio de la mayor función entera consiste en todos los números realesR y el rango consiste en el conjunto de enterosZ. Esta función a menudo se llama la función de piso 56 y tiene muchas aplicaciones en ciencias de la computación.
Claves para llevar
- Trazar puntos para determinar la forma general de las funciones básicas. Se debe memorizar la forma, así como el dominio y el rango, de cada uno.
- Las funciones polinómicas básicas son:f(x)=c,f(x)=x,f(x)=x2, yf(x)=x3.
- Las funciones básicas no polinómicas son:f(x)=|x|,f(x)=√x, yf(x)=1x.
- Una función cuya definición cambia dependiendo del valor en el dominio se llama función por partes. El valor en el dominio determina la definición apropiada a utilizar.
Ejercicio2.4.2
Coincidir la gráfica con la definición de función.
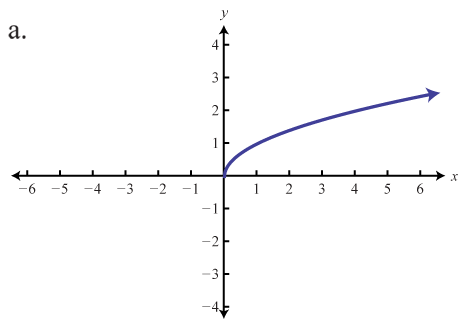
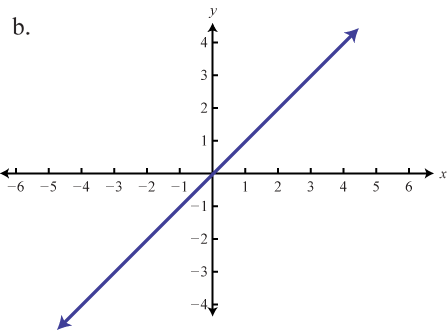
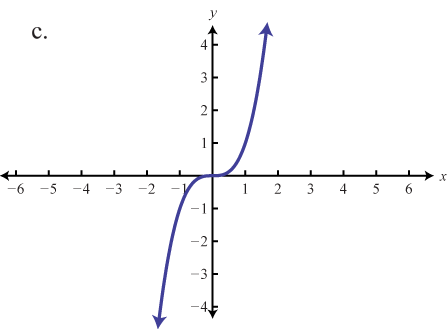
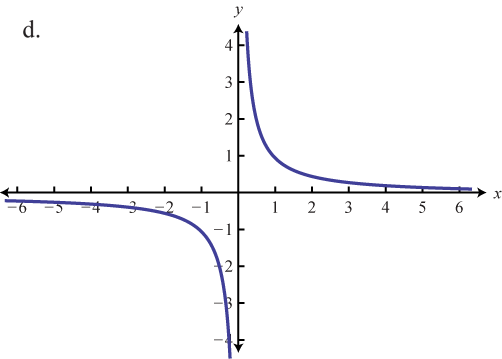
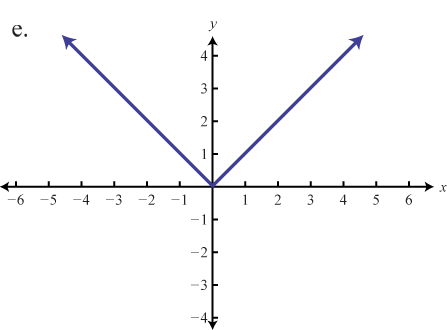
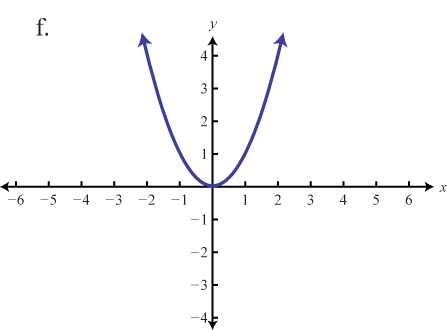
- f(x)=x
- f(x)=x2
- f(x)=x3
- f(x)=|x|
- f(x)=x
- f(x)=1x
- Contestar
-
1. b
3. c
5. a
Ejercicio2.4.3
Evaluar.
- f(x)=x; encontrarf(−10),f(0), yf(a).
- f(x)=x2; encontrarf(−10),f(0), yf(a).
- f(x)=x3; encontrarf(−10),f(0), yf(a).
- f(x)=|x|; encontrarf(−10),f(0), yf(a).
- f(x)=√x;findf(25),f(0), yf(a) dóndea≥0.
- f(x)=1x; encontrarf(−10),f(15), yf(a) dondea≠0.
- f(x)=5; encontrarf(−10),f(0), yf(a).
- f(x)=−12; encontrarf(−12),f(0), yf(a).
- Graficarf(x)=5 y exponer su dominio y rango.
- Graficarf(x)=−9 y exponer su dominio y rango
- Contestar
-
1. f(−10)=−10,f(0)=0,f(a)=a
3. f(−10)=−1,000,f(0)=0,f(a)=a3
5. f(25)=5,f(0)=0,f(a)=√a
7. f(−10)=5,f(0)=5,f(a)=5
9. Dominio:R; rango{5}
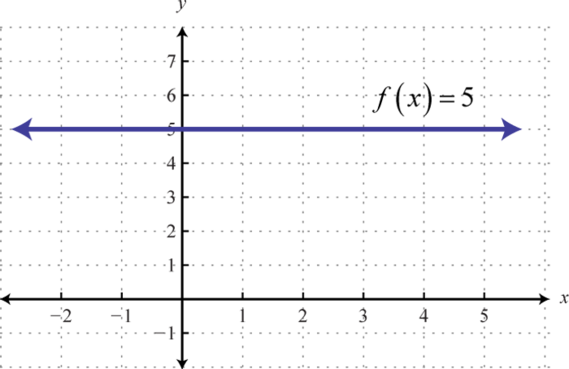
Figura2.4.23
Ejercicio2.4.4
Función de raíz cubicada.
- 17. Encuentra puntos en la gráfica de la función definida porf(x)=3√x conx -valores en el conjunto{−8,−1,0,1,8}.
- Encuentra puntos en la gráfica de la función definida porf(x)=3√x conx -valores en el conjunto{−3,−2,1,2,3}. Usa una calculadora y redondea a la décima más cercana.
- Grafica la función de raíz cúbica definidaf(x)=3√x por trazando los puntos encontrados en los dos ejercicios anteriores.
- Determinar el dominio y el rango de la función de raíz cúbica.
- Contestar
-
1. {(−8,−2),(−1,−1),(0,0),(1,1),(8,2)}
3.
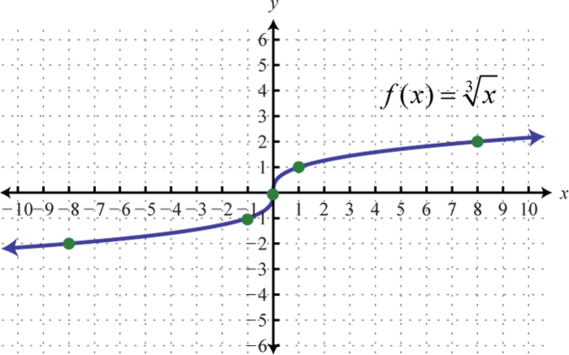
Figura2.4.24
Ejercicio2.4.5
Encuentra el par ordenado que especifica el puntoP.
1.
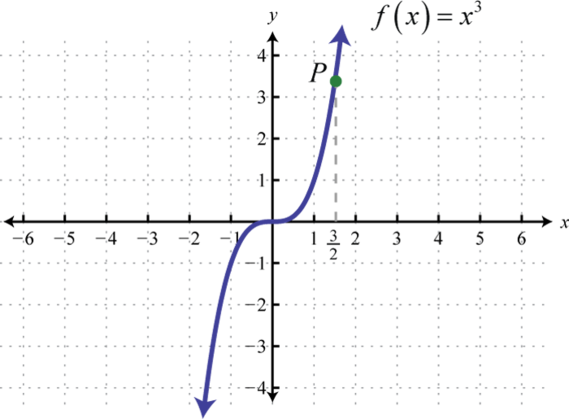
2.
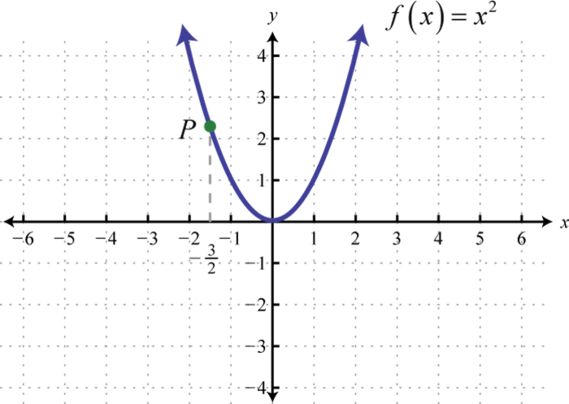
3.
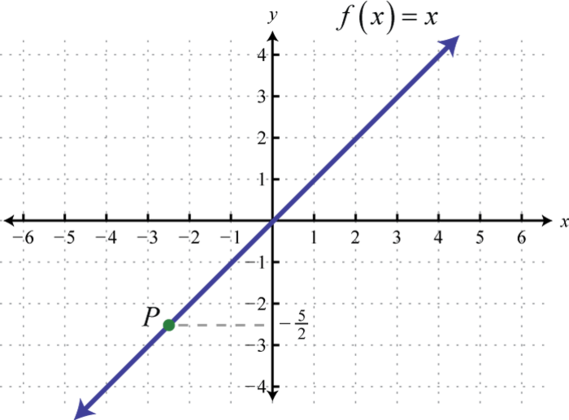
4.
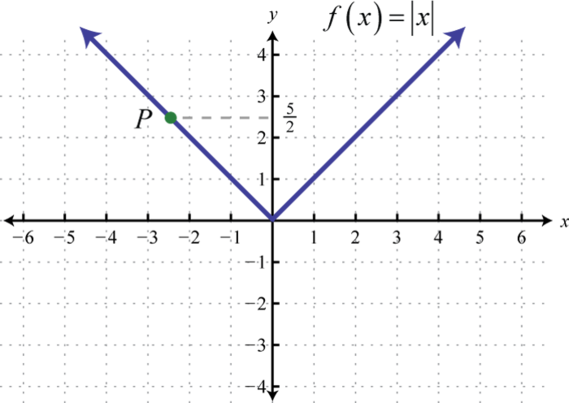
- Contestar
-
1. (32,278)
3. (−52,−52)
Ejercicio2.4.6
Grafica las funciones por tramos.
- g(x)={2 if x<0x if x≥0
- g(x)={x2 if x<03 if x≥0
- h(x)={x if x<0√x if x≥0
- h(x)={|x| if x<0x3 if x≥0
- f(x)={|x| if x<24 if x≥2
- f(x)={x if x<1√x if x≥1
- g(x)={x2 if x≤−1x if x>−1
- g(x)={−3 if x≤−1x3 if x>−1
- h(x)={0 if x≤01x if x>0
- h(x)={1x if x<0x2 if x≥0
- f(x)={x2 if x<0x if 0≤x<2−2 if x≥2
- f(x)={x if x<−1x3 if −1≤x<13 if x≥1
- g(x)={5 if x<−2x2 if −2≤x<2x if x≥2
- g(x)={x if x<−3|x| if −3≤x<1√x if x≥1
- h(x)={1x if x<0x2 if 0≤x<24 if x≥2
- h(x)={0 if x<0x3 if 0<x≤28 if x>2
- f(x)=[[[x+0.5]]
- f(x)=[[x]]+1
- f(x)=[[0.5x]]
- f(x)=2[[x]]
- Contestar
-
1.
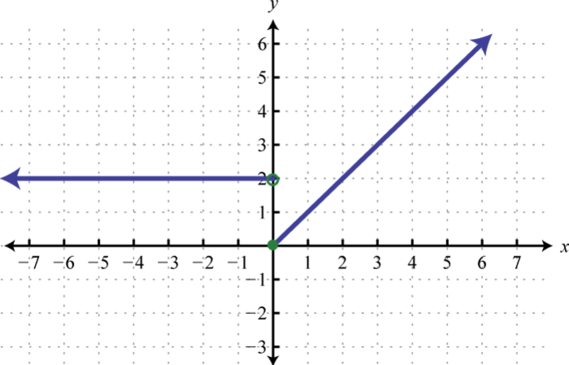
Figura2.4.29 3.
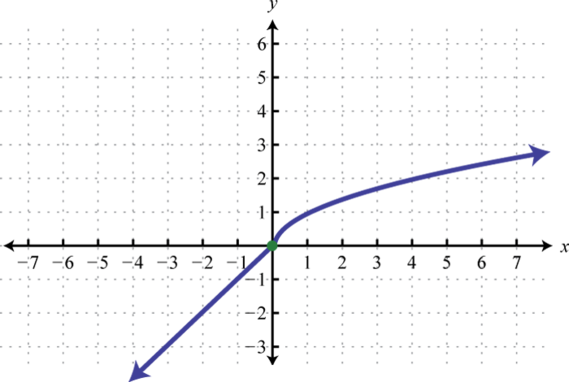
Figura2.4.50 5.
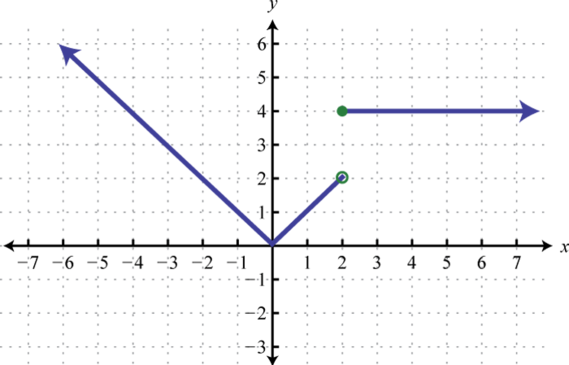
Figura2.4.51 7.
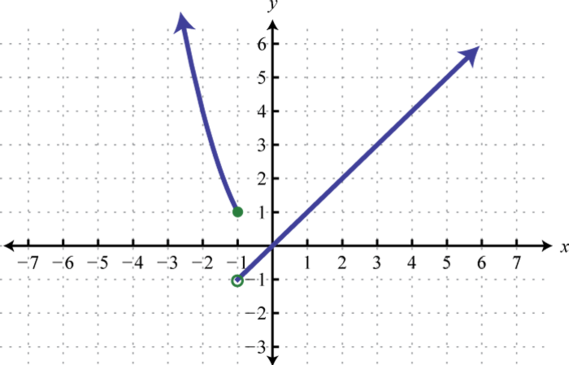
Figura2.4.52 9.
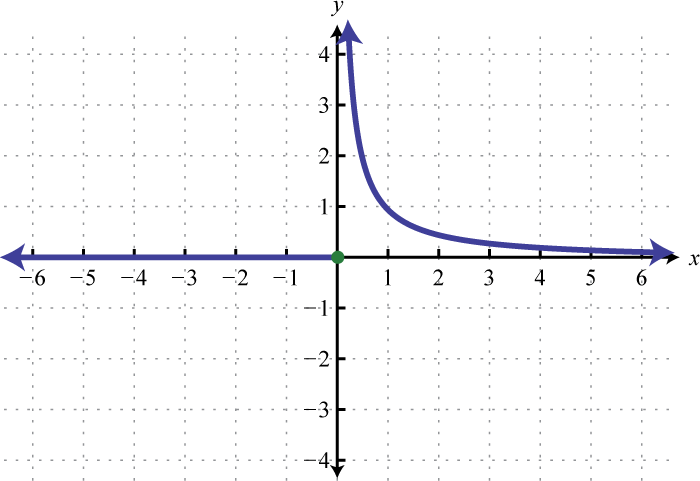
Figura2.4.53 11.
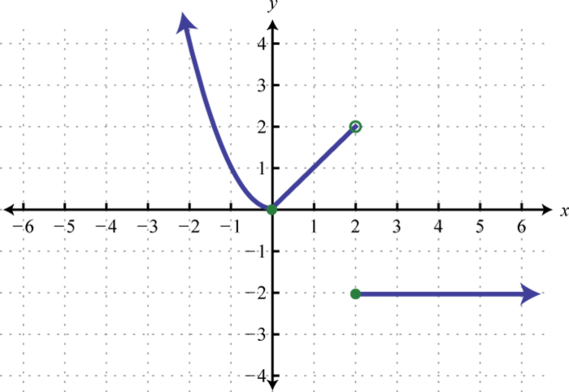
Figura2.4.54 13.
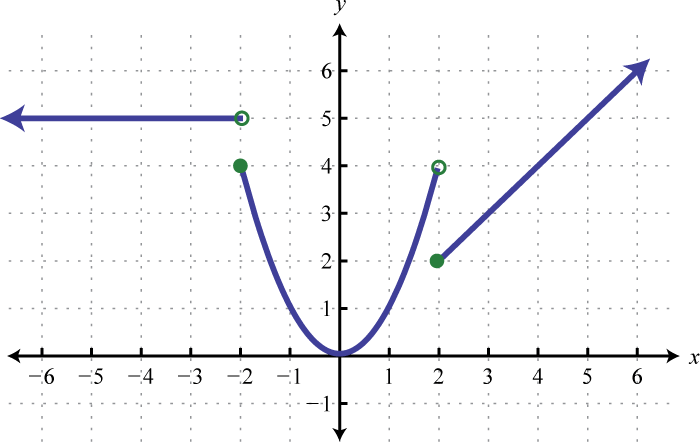
Figura2.4.55 15.
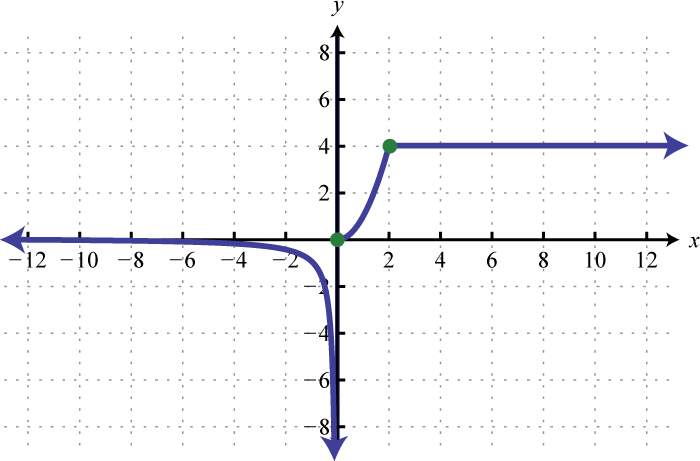
Figura2.4.56 17.
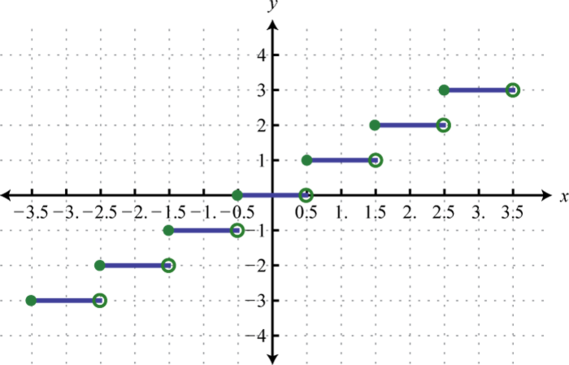
Figura2.4.57 19.
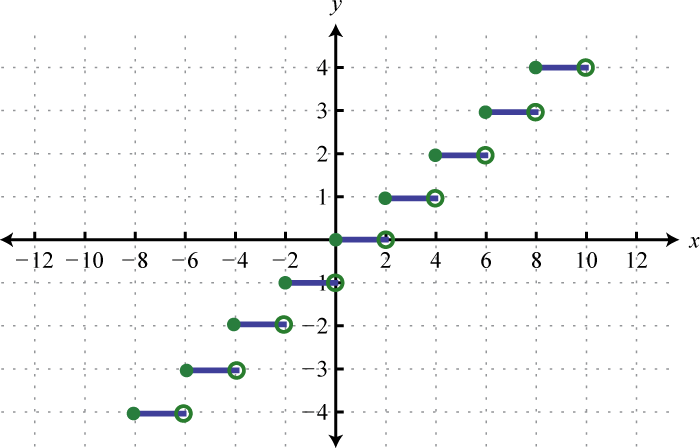
Figura2.4.58
Ejercicio2.4.7
Evaluar.
1. f(x)={x2 if x≤0x+2 if x>0
Encontrarf(−5),f(0), yf(3).
2. f(x)={x3 if x<02x−1 if x≥0
Encontrarf(−3),f(0), yf(2).
3. g(x)={5x−2 if x<1√x if x≥1
Encontrarg(−1),g(1), yg(4).
4. g(x)={x3 if x≤−2|x| if x>−2
Encontrarg(−3),g(−2), yg(−1).
5. h(x)={−5 if x<02x−3 if 0≤x<2x2 if x≥2
Encontrarh(−2),h(0), yh(4).
6. h(x)={−3x if x≤0x3 if 0<x≤4√x if x>4
Encontrarh(−5),h(4), yh(25).
7. f(x)=[[x−0.5]]
Encontrarf(−2),f(0), yf(3).
8. f(x)=[[2x]]+1
Encontrarf(−1.2),f(0.4), yf(2.6).
- Contestar
-
1. f(−5)=25,f(0)=0, yf(3)=5
3. g(−1)=−7,g(1)=1, yg(4)=2
5. h(−2)=−5,h(0)=−3, yh(4)=16
7. f(−2)=−3,f(0)=−1, yf(3)=2
Ejercicio2.4.8
Evaluar dada la gráfica def.
1. Encontrarf(−4),f(−2), yf(0).
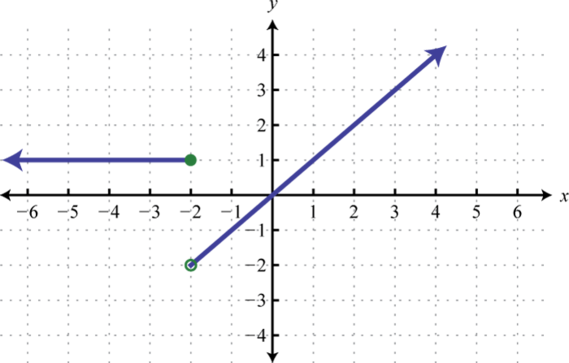
2. Encontrarf(−3),f(0), yf(1).
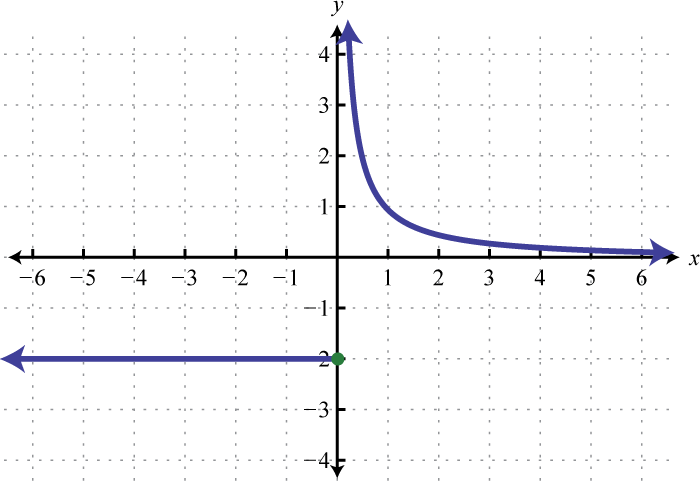
3. Encontrarf(0),f(2), yf(4).
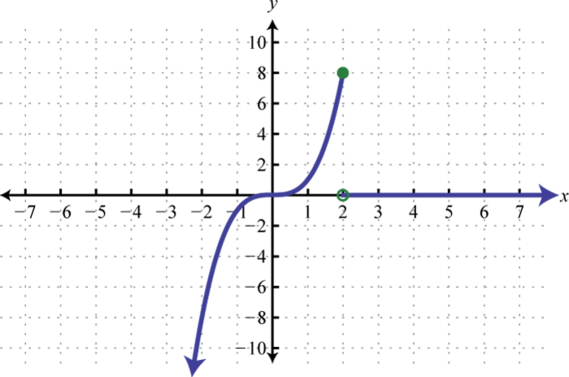
4. Encontrarf(−5),f(−2), yf(2).
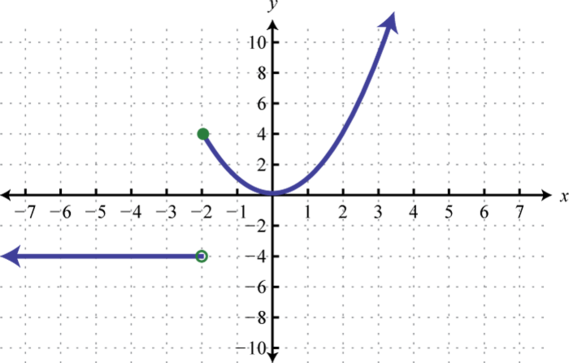
5. Encontrarf(−3),f(−2), yf(2).

6. Encontrarf(−3),f(0), yf(4).
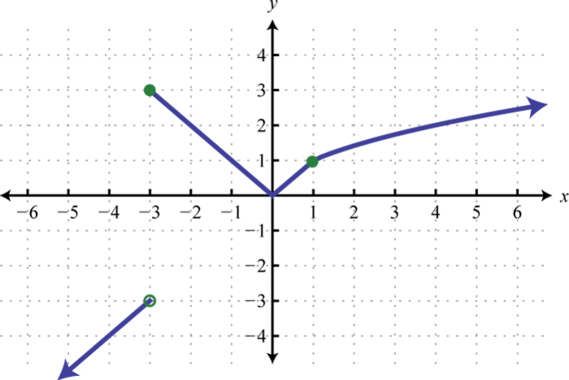
7. Encontrarf(−2),f(0), yf(2).
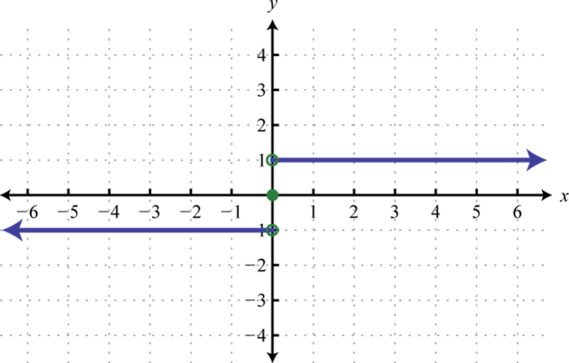
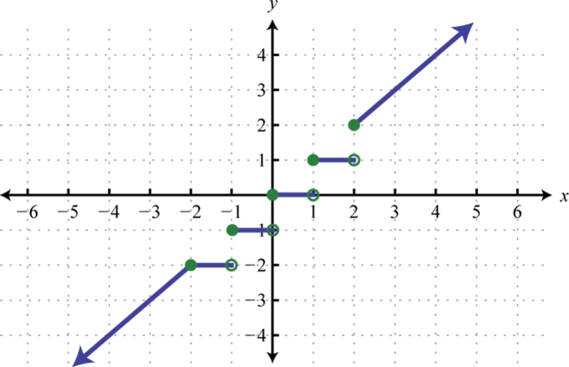
8. Encontrarf(−3),f(1), yf(2).
9. El valor de un automóvil en dólares se da en términos del número de años desde que se compró nuevo en1975:

(1) Determinar el valor del automóvil en el año1980.
(2) ¿En qué año se valora el automóvil$9,000?
10. El costo por unidad en dólares de lámparas personalizadas depende del número de unidades producidas de acuerdo a la siguiente gráfica:
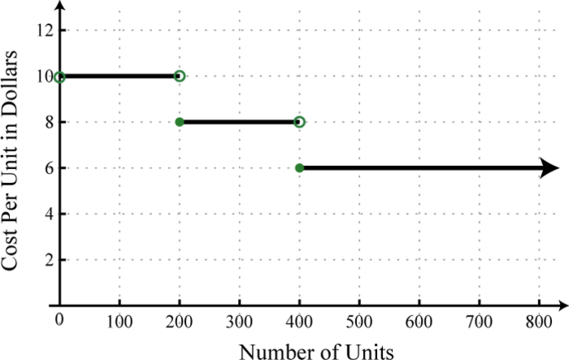
(1) ¿Cuál es el costo por unidad si se producen lámparas250 personalizadas?
(2) ¿Qué nivel de producción minimiza el costo por unidad?
11. Un vendedor de automóviles gana una comisión basada en las ventas totales cada mesx según la función:
(x)={0.03x if 0≤x<$20,0000.05x if $20,000≤x<$50,0000.07x if x≥$50,000
(1) Si las ventas totales del vendedor para el mes son$35,500, ¿cuál es su comisión según la función?
(2) Para alcanzar el siguiente nivel en la estructura de comisiones, ¿cuánto más en ventas necesitará?
12. Un barco de alquiler cuesta$32 por una hora, y cada hora adicional o parcial cuesta$8. Grafique el costo de la embarcación de alquiler y determine el costo para rentar la embarcación por412 horas.
- Contestar
-
1. f(−4)=1,f(−2)=1, yf(0)=0
3. f(0)=0,f(2)=8, yf(4)=0
5. f(−3)=5,f(−2)=4, yf(2)=2
7. f(−2)=−1,f(0)=0, yf(2)=1
9. (1)$3,000; (2)2005
11. (1)$1,775; (2)$14,500
Ejercicio2.4.9
- Explique a un estudiante principiante de álgebra qué es una asíntota.
- Investigar y discutir la diferencia entre las funciones de piso y techo. ¿Qué aplicaciones puedes encontrar que utilicen estas funciones?
- Contestar
-
1. La respuesta puede variar
Notas al pie
43 Cualquier función de la formaf(x)=c dondec es un número real.
44 La función lineal definida porf(x)=x.
45 La función cuadrática definida porf(x)=x2.
46 La gráfica curva formada por la función de cuadratura.
47 La función cúbica definida porf(x)=x3.
48 La función definida porf(x)=|x|.
49 La función definida porf(x)=√x.
50 La función definida porf(x)=1x.
51 Una línea vertical a la que una gráfica se acerca infinitamente.
52 Una línea horizontal a la que una gráfica se acerca infinitamente a donde tiendenx los valores -hacia±∞.
53 Una función cuya definición cambia dependiendo de los valores en el dominio.
54 Término que se usa cuando se refiere a una función por partes.
55 La función que asigna cualquier número realx al mayor entero menor o igual quex denotadof(x)=[[x]].
56 Un término que se usa cuando se refiere a la mayor función entera.


