2.3: Modelado de Funciones Lineales
- Page ID
- 109879
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Determinar la ecuación de una línea dada dos puntos.
- Determinar la ecuación de una línea dada la pendiente y\(y\) -interceptar.
- Encuentra funciones lineales que modelan aplicaciones comunes.
Ecuaciones de Líneas
Dada la ecuación algebraica de una línea, podemos graficarla de varias maneras. En esta sección, se nos dará una descripción geométrica de una línea y encontraremos la ecuación algebraica. Encontrar la ecuación de una línea se puede lograr de varias maneras. El siguiente ejemplo hace uso de la forma pendiente-intercepción,\(y = mx + b\), o el uso de la notación de función,\(f (x) = mx + b\). Si podemos determinar la pendiente,\(m\), y la\(y\) intersección,\((0, b)\), entonces podemos construir la ecuación.
Ejemplo\(\PageIndex{1}\):
Encuentra la ecuación de la línea que pasa por\((−3, 6)\) y\((5, −4)\).
Solución
Comenzamos por encontrar la pendiente. Dados dos puntos, podemos encontrar la pendiente usando la fórmula del talud.
\(\begin{array} { l l } { \left( x _ { 1 } , y _ { 1 } \right) } & { \left( x _ { 2 } , y _ { 2 } \right) } \\ { ( - 3,6 ) } & { ( 5 , - 4 ) } \end{array}\)
\(\begin{aligned} m & = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } \\ & = \frac { - 4 - ( 6 ) } { 5 - ( - 3 ) } \\ & = \frac { - 4 - 6 } { 5 + 3 } \\ & = \frac { - 10 } { 8 } \\ & = - \frac { 5 } { 4 } \end{aligned}\)
Aquí\(m = −\frac{5}{4}\) y tenemos
\(\begin{array} { l } { f ( x ) = m x + b } \\ { f ( x ) = - \frac { 5 } { 4 } x + b } \end{array}\)
Para encontrar\(b\), sustituya cualquiera de los puntos dados por los que pasa la línea. Aquí usaremos\((−3, 6)\), pero\((5, −4)\) funcionaría igual de bien:
\(\begin{aligned} f ( x ) & = - \frac { 5 } { 4 } x + b \quad\quad\color{Cerulean} {Use (x, f(x))=(-3,6)} \\ \color{OliveGreen}{6} & \color{Black}{=} - \frac { 5 } { 4 } ( \color{OliveGreen}{- 3}\color{Black}{ )} + b \\ 6 & = \frac { 15 } { 4 } + b \\ \frac { 6 \cdot \color{Cerulean}{4} } { \color{Black}{1} \cdot \color{Cerulean}{4} } - \frac { 15 } { 4 } & = b \\ \frac { 24-15 } { 4 } - 15 \\ \frac { 9 } { 4 } & = b \end{aligned}\)
Por lo tanto, la ecuación de la línea que pasa por los dos puntos dados es:
\(\begin{array} { l } { f ( x ) = m x \:\:+\:\: b } \\ \quad\quad\quad\quad\color{Cerulean}{\downarrow\quad\:\:\:\:\:\downarrow} \\ { f ( x ) = - \frac { 5 } { 4 } x + \frac { 9 } { 4 } } \end{array}\)
Contestar
\[f ( x ) = - \frac { 5 } { 4 } x + \frac { 9 } { 4 }\]
A continuación, se esboza un método alternativo para encontrar ecuaciones de líneas. Comience aplicando la fórmula de pendiente con un punto dado\((x_{1} , y_{1})\) y un punto variable\((x, y)\).
\(\begin{aligned} m & = \frac { y - y _ { 1 } } { x - x _ { 1 } } \\ \frac { m } { 1 } & = \frac { y - y _ { 1 } } { x - x _ { 1 } } \quad\quad\color{Cerulean}{Cross \:multiply}\\ m \left( x - x _ { 1 } \right) & = y - y _ { 1 } \quad\quad\color{Cerulean}{Apply \:the \:symmetric\: property}\\ \left( y - y _ { 1 } \right) & = m \left( x - x _ { 1 } \right) \end{aligned}\)
Por lo tanto, la ecuación de una línea no vertical se puede escribir en forma de pendiente de punto 30:
\(y - y _ { 1 } = m \left( x - x _ { 1 } \right) \quad\color{Cerulean}{Point-slope\: form.}\)
La forma de pendiente puntual es particularmente útil para encontrar la ecuación de una línea dada la pendiente y cualquier solución de par ordenado. Después de encontrar la pendiente,\(−\frac{5}{4}\) en el ejemplo anterior, podríamos usar esta forma para encontrar la ecuación.
\(\begin{array} { l } { \color{Cerulean} { Point \quad\quad Slope } } \\ { \left( x _ { 1 } , y _ { 1 } \right) } \\ { ( - 3,6 ) \quad m = - \frac { 5 } { 4 } } \end{array}\)
Sustituir de la siguiente manera.
\(\begin{aligned} y - y _ { 1 } & = \color{Cerulean}{m} \color{Black}{\left( x - x _ { 1 } \right)} \\ y - ( \color{OliveGreen}{6}\color{Black}{ )} & = \color{Cerulean}{- \frac { 5 } { 4 } }\color{Black}{(} x - (\color{OliveGreen}{ - 3}\color{Black}{ )} ) \quad \color {Cerulean} { Solve\:for\: y } \\ y - 6 & = - \frac { 5 } { 4 } ( x + 3 ) \quad\quad\color{Cerulean} { Distribute } \\ y - 6 & = - \frac { 5 } { 4 } x - \frac { 15 } { 4 } \\ y & = - \frac { 5 } { 4 } x - \frac { 15 } { 4 } +6 \\ y & = - \frac { 5 } { 4 } x + \frac { 9 } { 4 } \end{aligned}\)
Observe que obtenemos la misma función lineal\(f ( x ) = - \frac { 5 } { 4 } x + \frac { 9 } { 4 }\).
En ocasiones una variable no se expresa explícitamente en términos de otra; sin embargo, todavía se asume que una variable depende de la otra. Por ejemplo, la ecuación representa\(2x + 3y = 6\) implícitamente la\(f (x) = −\frac{2}{3}x + 2\) función.Debe sentirse cómodo trabajando con funciones en cualquiera de las dos formas.
Ejemplo\(\PageIndex{2}\)
Encuentra la ecuación de la siguiente función lineal:
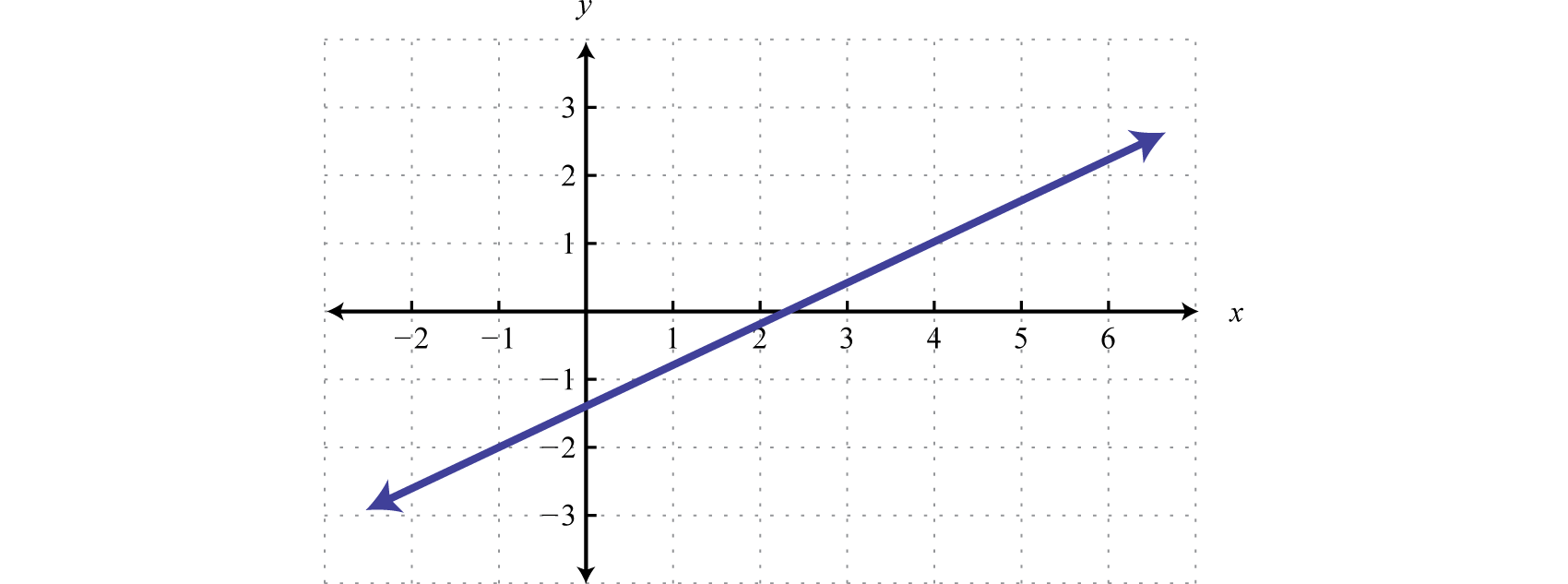
Solución
A partir de la gráfica podemos determinar dos puntos\((−1, −2)\) y\((4, 1)\). Usa estos puntos para leer la pendiente de la gráfica. El ascenso son\(3\) unidades y la carrera es\(5\) unidades.
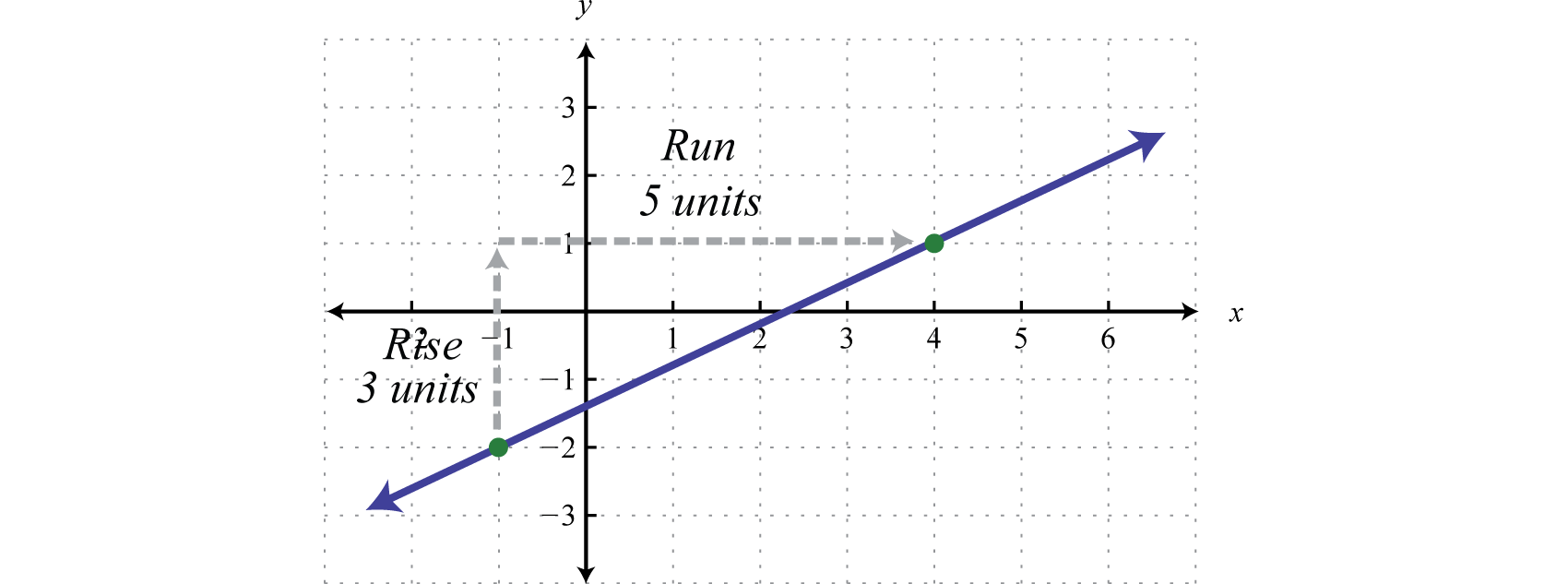
Por lo tanto, tenemos la pendiente y un punto. (No importa cuál de los puntos dados usemos, el resultado será el mismo.)
\(\begin{array} { l } { \color{Cerulean} { Point } }\quad\quad\:\:\color{Cerulean}{Slope} \\ { ( - 1 , - 2 ) \quad m = \frac { 3 } { 5 } } \end{array}\)
Utilice la forma de punto-pendiente para determinar la ecuación de la línea.
\(\begin{aligned} y - y _ { 1 } & = \color{Cerulean}{m} \color{Black}{\left( x - x _ { 1 } \right)} \\ y - ( \color{OliveGreen}{- 2}\color{Black}{ )} & = \color{Cerulean}{\frac { 3 } { 5 }} \color{Black}{(} x - ( \color{OliveGreen}{- 1}\color{Black}{ )} ) \quad \color {Cerulean} { Solve\: for\: y. } \\ y + 2 & = \frac { 3 } { 5 } ( x + 1 ) \\ y + 2 & = \frac { 3 } { 5 } x + \frac { 3 } { 5 } \\ y & = \frac { 3 } { 5 } x + \frac { 3 } { 5 } - 2 \\ y & = \frac { 3 } { 5 } x - \frac { 7 } { 5 } \end{aligned}\)
Contestar
\[f(x)=\frac{3}{5}x−\frac{7}{5}\]
Recordemos que las líneas paralelas 31 son líneas en un mismo plano que nunca se cruzan. Dos líneas no verticales en un mismo plano con pendientes\(m_{1}\) y\(m_{2}\) son paralelas si sus pendientes son las mismas,\(m_{1} = m_{2}\).
Ejemplo\(\PageIndex{3}\)
Encuentra la ecuación de la línea que pasa a través\((3, −2)\) y paralela a\(x − 2y = −2\).
Solución
Para encontrar la pendiente de la línea dada, resuelva para\(y\).
\(\begin{aligned} x - 2 y & = - 2 \\ - 2 y & = - x - 2 \\ y & = \frac { - x - 2 } { - 2 } \\ y & = \frac { - x } { - 2 } - \frac { 2 } { - 2 } \\ y & = \frac { 1 } { 2 } x + 1 \end{aligned}\)
Aquí la línea dada tiene pendiente\(m = \frac{1}{2}\) y por lo tanto la pendiente de una línea\(m_{∥} = \frac{1}{2}\) paralela.La notación\(m_{∥}\) dice “\(m\)paralela”. Como se nos da un punto y ahora tenemos la pendiente, elegiremos usar la forma de punto-pendiente de una línea para determinar la ecuación.
\(\begin{array} { l l } { \color{Cerulean}{ Point } } & { \color{Cerulean}{ Slope } } \\ { ( 3 , - 2 ) } & { m _ { \| } = \frac { 1 } { 2 } } \end{array}\)
\(\begin{aligned} y - y _ { 1 } & = m \left( x - x _ { 1 } \right) \color{Cerulean}{Point-Slope\: form}\\ y - ( - 2 ) & = \frac { 1 } { 2 } ( x - 3 ) \\ y + 2 & = \frac { 1 } { 2 } x - \frac { 3 } { 2 } \\ y + 2 \color{Cerulean}{- 2} & = \frac { 1 } { 2 } x - \frac { 3 } { 2 } \color{Cerulean}{- 2} \\ y & = \frac { 1 } { 2 } x - \frac { 7 } { 2 } \end{aligned}\)
Contestar
\[f ( x ) = \frac { 1 } { 2 } x - \frac { 7 } { 2 }\]
Es importante tener una comprensión geométrica de esta cuestión. Se nos pidió encontrar la ecuación de una línea paralela a otra línea que pasaba por cierto punto.
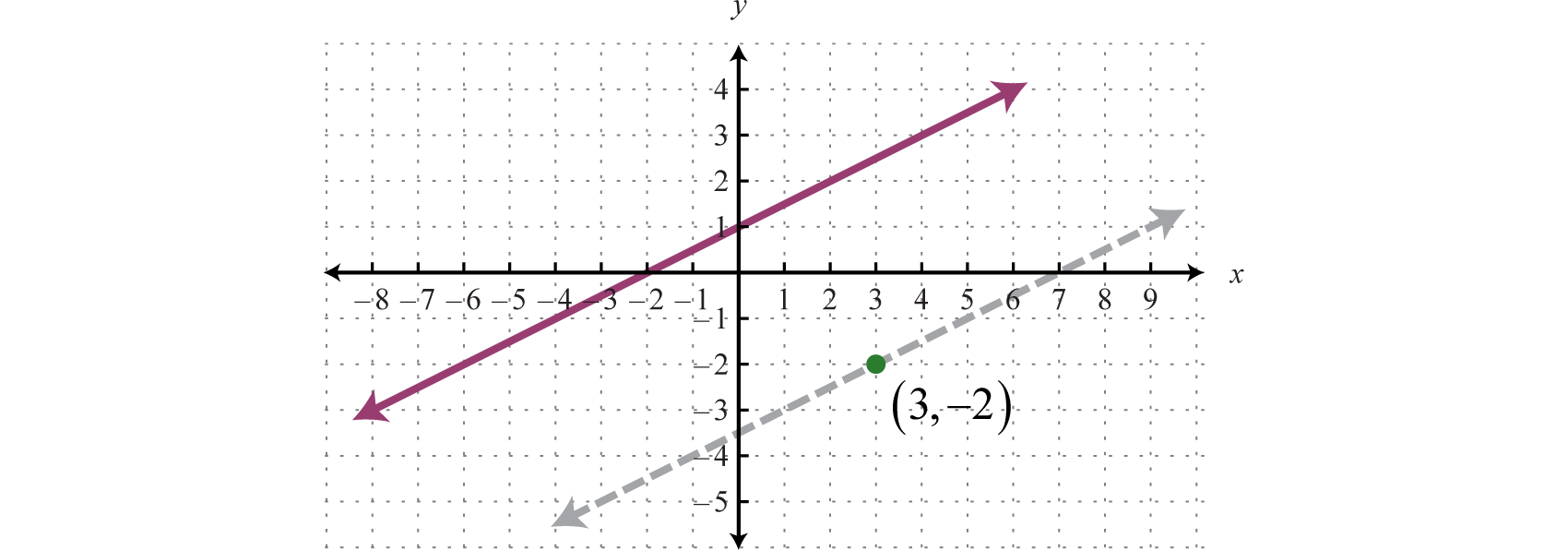
A través del punto\((3, −2)\) encontramos una línea paralela,\(y = \frac{1}{2} x − \frac{7}{2}\), mostrada como una línea discontinua. Observe que la pendiente es la misma que la línea dada\(y = \frac{1}{2} x + 1\), pero la\(y\) -intercepción es diferente.
Recordemos que las líneas 32 perpendiculares son líneas en el mismo plano que se cruzan en ángulos rectos (\(90\)grados). Dos líneas no verticales, en un mismo plano con pendientes\(m_{1}\) y\(m_{2}\), son perpendiculares si el producto de sus pendientes es\(−1\),\(m_{1} ⋅ m_{2} = −1\). Podemos resolver\(m_{1}\) y obtener\(m_{1} = −\frac{1}{m_{2}}\). De esta forma, vemos que las líneas perpendiculares tienen pendientes que son recíprocas negativas 33, u recíprocas opuestas 34. En general, dados los números reales a y b,
\(\text{If}\: m = \frac { a } { b } \text { then } m _ { \perp } = - \frac { b } { a }\)
La notación matemática\(m_{⊥}\) dice “\(m\)perpendicular”. Por ejemplo, el recíproco opuesto de\(m = −\frac{3}{5}\) es\(m⊥ = \frac{5}{3}\). Podemos verificar que dos pendientes produzcan líneas perpendiculares si su producto es\(−1\).
\(m \cdot m _ { \perp } = - \frac { 3 } { 5 } \cdot \frac { 5 } { 3 } = - \frac { 15 } { 15 } = - 1\color{Cerulean}{✓}\)
Ejemplo\(\PageIndex{4}\):
Encuentra la ecuación de la línea que pasa a través\((−5, −2)\) y perpendicular a\(x + 4y = 4\).
Solución
Para encontrar la pendiente de la línea dada, resuelva para\(y\).
\(\begin{aligned} x + 4 y & = 4 \\ 4 y & = - x + 4 \\ y & = \frac { - x + 4 } { 4 } \\ y & = \frac { - x } { 4 } + \frac { 4 } { 4 } \\ y & = - \frac { 1 } { 4 } x + 1 \end{aligned}\)
La línea dada tiene pendiente\(m = −\frac{1}{4}\), y por lo tanto,\(m⊥ = +\frac{4}{1} = 4\). Sustituya esta pendiente y el punto dado en forma de punto-pendiente.
\(\begin{array} { l l } { \color{Cerulean} { Point } } & { \color{Cerulean} { Slope } } \\ { ( - 5 , - 2 ) } & { m _ { \perp } = 4 } \end{array}\)
\(\begin{aligned} y - y _ { 1 } & = m \left( x - x _ { 1 } \right) \\ y - ( - 2 ) & = 4 ( x - ( - 5 ) ) \\ y + 2 & = 4 ( x + 5 ) \\ y + 5 & = 4 x + 20 \\ y & = 4 x + 18 \end{aligned}\)
Contestar
\[f(x)=4x+18\]
Geométricamente, vemos que la línea\(y=4x+18\), mostrada como una línea discontinua en la gráfica, pasa\((-5, -2)\) y es perpendicular a la línea dada\(y=\frac{1}{4}x+1\).
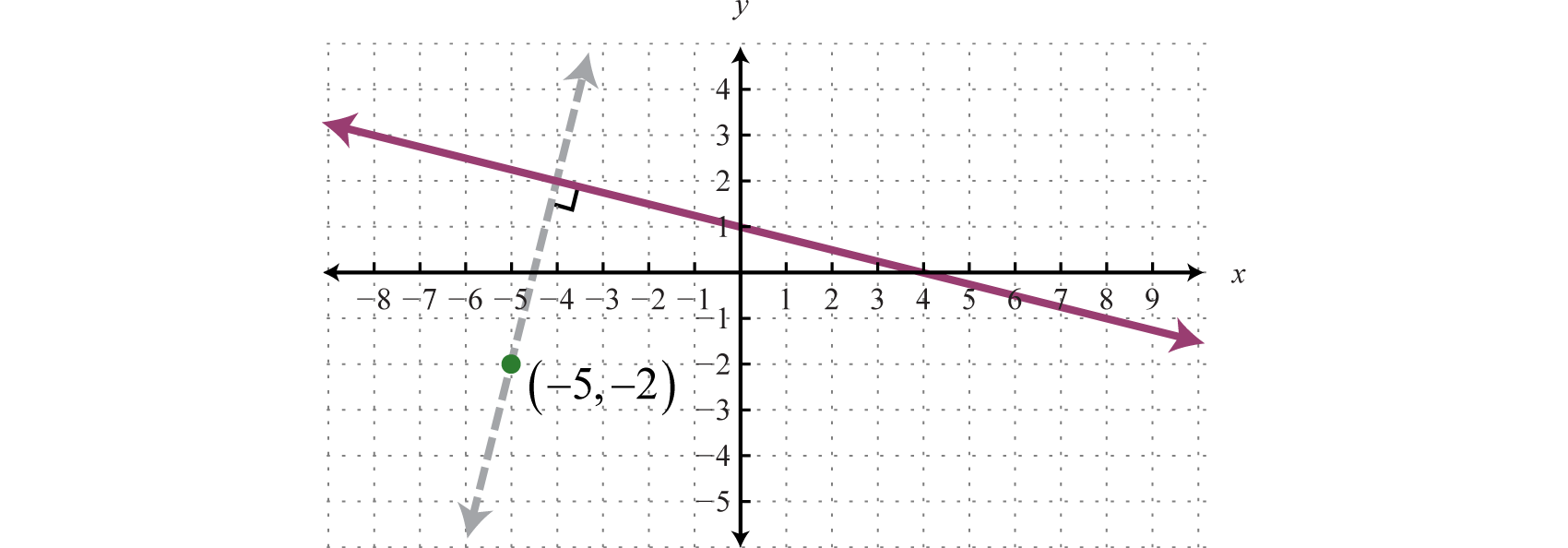
Ejercicio\(\PageIndex{1}\)
Encuentra la ecuación de la línea que pasa a través\((−5, −2)\) y perpendicular a\(\frac{1}{3} x − \frac{1}{2} y = −2\).
- Contestar
-
\(y = - \frac { 3 } { 2 } x - \frac { 19 } { 2 }\)
www.youtube.com/v/ncnjw7jd2sk
Modelado de Aplicaciones Lineales
Los datos se pueden utilizar para construir funciones que modelan aplicaciones del mundo real. Una vez determinada una ecuación que se ajusta a datos dados, podemos usar la ecuación para hacer ciertas predicciones; esto se llama modelado matemático 35.
Ejemplo\(\PageIndex{5}\):
El costo de un alquiler diario de camiones es\($48.00\), más un adicional\($0.45\) por cada milla conducida. Escribe una función que dé el costo del alquiler diario de camiones y utilízala para determinar el costo total de rentar la camioneta por un día y conducirla\(60\) millas.
Solución
El costo total del alquiler de camiones depende del número de millas recorridas. Si dejamos\(x\) representar el número de millas recorridas, entonces\(0.45x\) representa el costo variable de rentar el camión. Usa esto y el costo fijo,\($48.00\), para escribir una función que modele el costo total,
\(C ( x ) = 0.45 x + 48\)
Utilice esta función para calcular el costo del alquiler cuando\(x = 60\) millas.
\(\begin{aligned} C ( 60 ) & = 0.45 ( 60 ) + 48 \\ & = 27 + 48 \\ & = 75 \end{aligned}\)
Respuesta:
El costo total de rentar la camioneta para el día y manejarla\(60\) millas sería\($75\).
Podemos usar el modelo\(C (x) = 0.45x + 48\) para responder muchas más preguntas. Por ejemplo, ¿cuántas millas se pueden recorrer para mantener como máximo el costo del alquiler\($66\)? Para responder a esta pregunta, establecer una desigualdad que exprese el costo menor o igual a\($66\).
\(\begin{aligned} C ( x ) & \leq \$ 66 \\ 0.45 x + 48 & \leq 66 \end{aligned}\)
Resuelva\(x\) para determinar el número de millas que se pueden conducir.
\(\begin{aligned} 0.45 x + 48 & \leq 66 \\ 0.45 x & \leq 18 \\ x & \leq 40 \end{aligned}\)
Para limitar el costo de alquiler a\($66\), el camión se puede conducir\(40\) millas o menos.
Ejemplo\(\PageIndex{6}\):
Una empresa compró una nueva pieza de equipo para\($12,000\). Cuatro años después se valoró en\($9,000\) dólares. Utilice estos datos para construir una función lineal que modele el valor de la pieza de equipo a lo largo del tiempo.
Solución
El valor del artículo depende del número de años posteriores a su compra. Por lo tanto, la edad del equipo es la variable independiente. Utilice pares ordenados donde los\(x\) valores -representan la edad y los\(y\) valores -representan el valor correspondiente.
\((age, value)\)
A partir del problema, podemos determinar dos pares ordenados. Se compró nuevo\((age = 0)\), el costo del artículo\($12,000\), y\(4\) años después el artículo se valoró en\($9,000\). Por lo tanto, podemos escribir los siguientes dos pares\((age, value)\) ordenados:
\(( 0,\:12,000 ) \quad \text { and } \quad ( 4,\: 9,000 )\)
Utilice estos dos pares ordenados para construir un modelo lineal. Comience por encontrar la pendiente\(m\).
\(\begin{aligned} m & = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } \\ & = \frac { 9,000 - 12,000 } { 4 - 0 } \\ & = \frac { - 3,000 } { 4 } \\ & = - 750 \end{aligned}\)
Aquí tenemos\(m = −750\). El par ordenado\((0, 12,000)\) da la\(y\) -intercepción; por lo tanto,\(b = 12,000\).
\(\begin{array} { l } { y = m x + b } \\ { y = - 750 x + 12,000 } \end{array}\)
Por último, escribir este modelo como una función que dé el valor de la pieza de equipo a lo largo del tiempo. Elija el nombre de la función\(V\), el valor y la variable\(t\) en lugar de\(x\) representar el tiempo en años.
\(V ( t ) = - 750 t + 12,000\)
Respuesta:
\(V ( t ) = - 750 t + 12,000\)
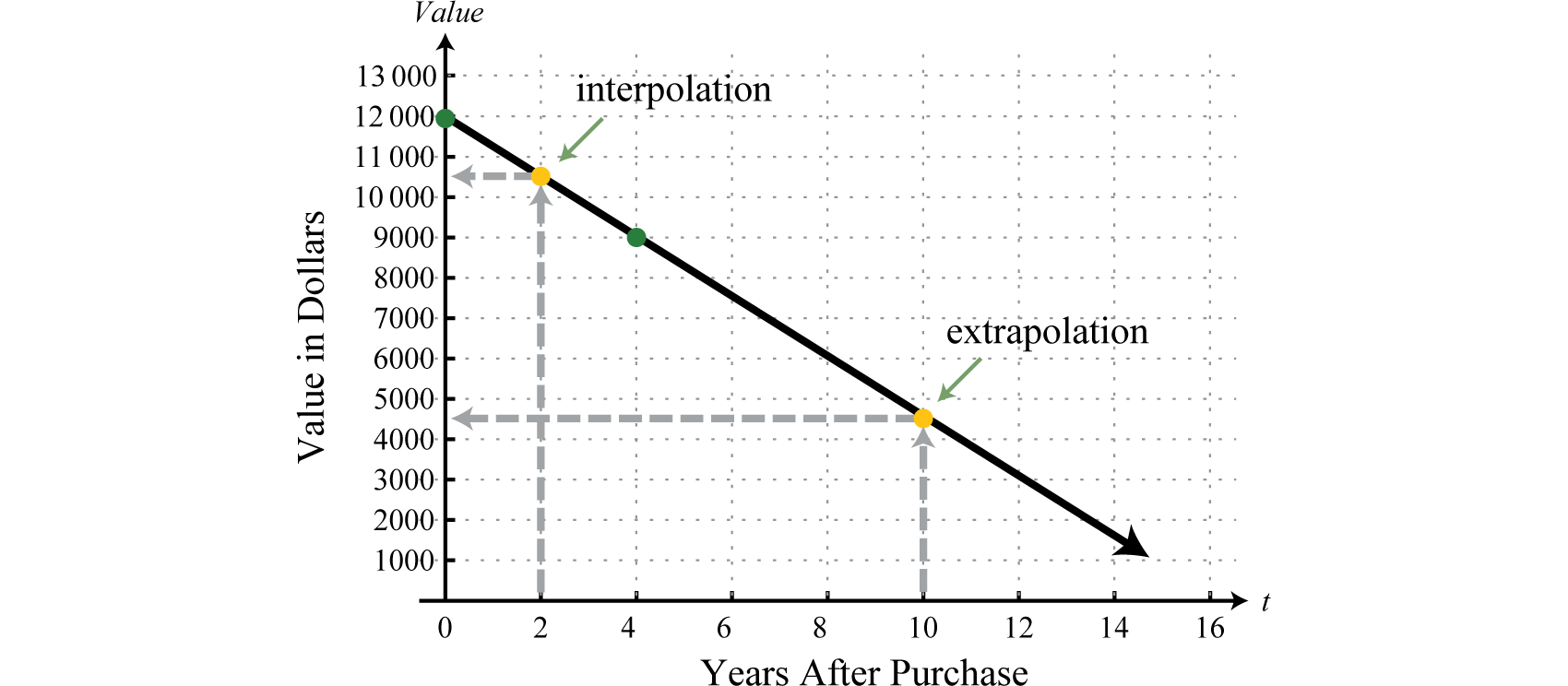
La función\(V (t) = −750t + 12,000\) denominada modelo de depreciación lineal 36. Utiliza una ecuación lineal para expresar el valor decreciente de un ítem a lo largo del tiempo. El uso de esta función para determinar el valor del ítem entre los puntos de datos dados se llama interpolación 37. Por ejemplo, podemos usar la función para determinar el valor del ítem donde\(t = 2\),
\(\begin{aligned} V ( 2 ) & = - 750 ( 2 ) + 12,000 \\ & = 10,500 \end{aligned}\)
La función muestra que el artículo valía\($10,500\) dos años después de su compra. El uso de este modelo para predecir el valor fuera de los puntos de datos dados se denomina extrapolación 38. Por ejemplo, podemos usar la función para determinar el valor del ítem cuando\(t = 10\):
\(\begin{aligned} V ( 10 ) & = - 750 ( 10 ) + 12,000 \\ & = - 7,500 + 12,000 \\ & = 4,500 \end{aligned}\)
El modelo predice que la pieza de equipo valdrá\($4,500\) diez años después de su compra.
En una aplicación de negocios, los ingresos resultan de la venta de una serie de artículos. Por ejemplo, si se puede vender un artículo\($150\) y dejamos\(n\) representar el número de unidades vendidas, entonces podemos formar la siguiente función de ingresos 39:
\(R(n)=150n\)
Utilice esta función para determinar los ingresos generados por la venta de\(n=100\) unidades,
\(R ( 100 ) = 150 ( 100 ) = 15,000\)
La función muestra que los ingresos generados por la venta de\(100\) artículos es\($15,000\). Por lo general, la venta de artículos no representa toda la historia. Hay una serie de costos asociados con la generación de ingresos. Por ejemplo, si hay una tarifa de instalación única de\($5,280\) y cada artículo cuesta\($62\) producir, entonces podemos formar la siguiente función de costo 40:
\(C ( n ) = 62 n + 5,280\)
Aquí\(n\) representa el número de artículos producidos. Utilice esta función para determinar el costo asociado a\(n = 100\) las unidades de producción:
\(C ( 100 ) = 62 ( 100 ) + 5,280 = 11,480\)
La función muestra que el costo asociado con la producción de 100 artículos es de $11,480. El beneficio es ingresos menos costos:
\(\begin{aligned} \color{Cerulean} { Profit } & = \color {Cerulean} { Revenue -Cost } \\ & = 15,000 - 11,480 \\ & = 3,520 \end{aligned}\)
Por lo tanto, el beneficio generado por la producción y venta de\(100\) artículos es\($3,520\). En general, dada una función de ingresos\(R\) y una función de costo\(C\), podemos formar una función de ganancia 41 restando de la siguiente manera:
\(P ( n ) = R ( n ) - C ( n )\)
Ejemplo\(\PageIndex{7}\):
El costo en dólares de producir n artículos viene dado por la fórmula\(C (n) = 62n + 5,280\). El ingreso en dólares viene dado por\(R (n) = 150n\), donde\(n\) representa el número de artículos vendidos. Escribir una función que dé el beneficio generado por la producción y venta de n artículos. Utilice la función para determinar cuántos artículos deben producirse y venderse para obtener una ganancia de al menos\($7,000\).
Solución
Obtener la función de beneficio restando la función de costo de la función de ingresos.
\(\begin{aligned} P ( n ) & = R ( n ) - C ( n ) \\ & = 150 n - ( 62 n + 5,280 ) \\ & = 150 n - 62 n - 5,280 \\ & = 88 n - 5,280 \end{aligned}\)
Por lo tanto,\(P (n) = 88n + 5,280\) modela el beneficio. Para determinar el número de artículos que deben producirse y venderse para obtener ganancias al menos\($7,000\), resuelva lo siguiente:
\(\begin{aligned} P ( n ) & \geq 7,000 \\ 88 n - 5,280 & \geq 7,000 \\ 88 n & \geq 12,280 \\ n & \geq 139.5 \end{aligned}\)
Redondear porque el número de unidades producidas y vendidas debe ser un número entero. Para ver esto, calcule el beneficio dónde\(n\) está\(139\) y\(140\) las unidades.
\(\begin{array} { l } { P ( 139 ) = 88 ( 139 ) - 5,280 = 6,952 } \\ { P ( 140 ) = 88 ( 140 ) - 5,280 = 7,040 } \end{array}\)
Respuesta:
\(140\)o más artículos deben ser producidos y vendidos con el fin de obtener un beneficio de al menos\($7,000\).
En ocasiones los costos superan los ingresos, en cuyo caso, la ganancia será negativa. Por ejemplo, utilizar la función de ganancia del ejemplo anterior,\(P (n) = 88n − 5,280\), para calcular el beneficio generado donde\(n = 50\).
\(P ( 50 ) = 88 ( 50 ) - 5,280 = - 880\)
Esto indica que cuando se producen y venden\(50\) unidades la utilidad correspondiente es una pérdida de\($880\).
A menudo es importante determinar cuántos artículos se deben producir y vender para alcanzar el punto de equilibrio. Romper el equilibrio significa no tener ni una ganancia ni una pérdida; en este caso, la ganancia será igual a cero. Para determinar el punto de equilibrio 42, establezca la función de ganancia igual a cero y resuelva:
\(\begin{aligned} P ( n ) & = 88 n - 5,280 \\ 0 & = 88 n - 5,280 \\ 5,280 & = 88 n \\ 60 & = n \end{aligned}\)
Por lo tanto,\(60\) los artículos deben ser producidos y vendidos para alcanzar el punto de equilibrio.

Ejercicio\(\PageIndex{2}\)
Se pueden vender camisetas personalizadas para\($6.50\) cada una. Además de una tarifa de instalación inicial de\($120\), cada camiseta cuesta\($3.50\) producir.
- Escribir una función que modele los ingresos y una función que modele el costo.
- Determinar una función que modele el beneficio y utilízelo para determinar el beneficio de producir y vender\(150\) camisetas.
- Calcula el número de playeras que deben venderse para igualar.
- Contestar
-
a. Ingresos:\(R (x) = 6.50x\); costo:\(C (x) = 3.50x + 120\);
b. beneficio:\(P (x) = 3x + 120\);\($330\)
c.\(40\)
Claves para llevar
- Dados dos puntos podemos encontrar la ecuación de una línea.
- Las líneas paralelas tienen la misma pendiente.
- Las líneas perpendiculares tienen pendientes que son recíprocas opuestas. En otras palabras, si\(m = \frac{a}{b}\), entonces\(m_{⊥} = −\frac{b}{a}\).
- Para encontrar una ecuación de una línea, primero use la información dada para determinar la pendiente. Luego usa la pendiente y un punto en la línea para encontrar la ecuación usando la forma de punto-pendiente.
- Para construir una función lineal que modele una aplicación del mundo real, primero identifique las variables dependientes e independientes. A continuación, encuentra dos pares ordenados que describan la situación dada. Utilice estos dos pares ordenados para construir una función lineal al encontrar la pendiente y la\(y\) intersección.
Ejercicio\(\PageIndex{3}\)
Encuentra la función lineal\(f\) que pasa por los puntos dados.
- \((−1, 2)\)y\((3, −4)\)
- \((3, −2)\)y\((−1, −4)\)
- \((−5, −6)\)y\((−4, 2)\)
- \((2, −7)\)y\((3, −5)\)
- \((10, −15)\)y\((7, −6)\)
- \((−9, 13)\)y\((−8, 12)\)
- \((−12, 22)\)y\((6, −20)\)
- \((6, −12)\)y\((−4, 13)\)
- \((\frac{1}{3}, \frac{4}{5})\)y\((\frac{1}{2} ,1)\)
- \((−\frac{3}{2}, −\frac{5}{2})\)y\((1, \frac{5}{6})\)
- \((−5, 10)\)y\((−1, 10)\)
- \((4, 0)\)y\((−7, 0)\)
- Contestar
-
1. \(f (x) = −\frac{3}{2} x + \frac{1}{2}\)
3. \(f (x) = 8x + 34\)
5. \(f (x) = −3x + 15\)
7. \(f (x) = −\frac{7}{3} x − 6\)
9. \(f (x) = \frac{6}{5} x + \frac{2}{5}\)
11. \(f (x) = 10\)
Ejercicio\(\PageIndex{4}\)
Encuentra la ecuación de la función lineal dada.
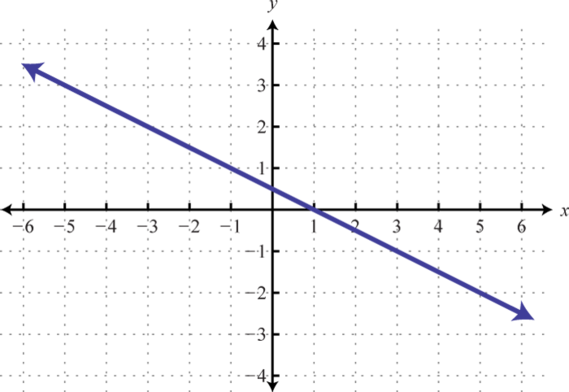
1.
2.
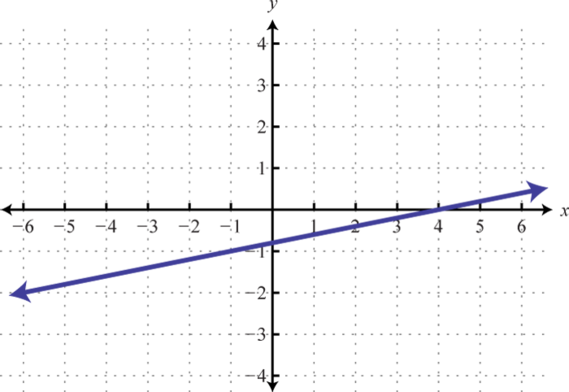
3.
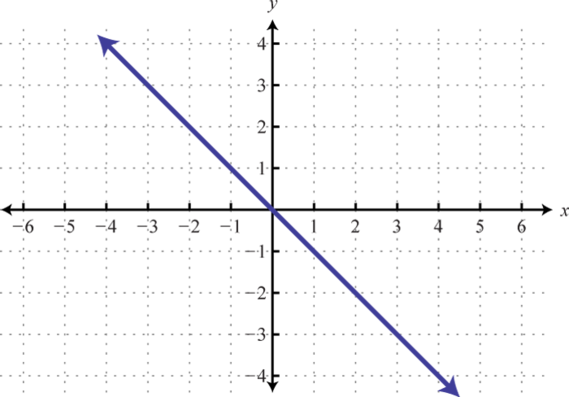
4.
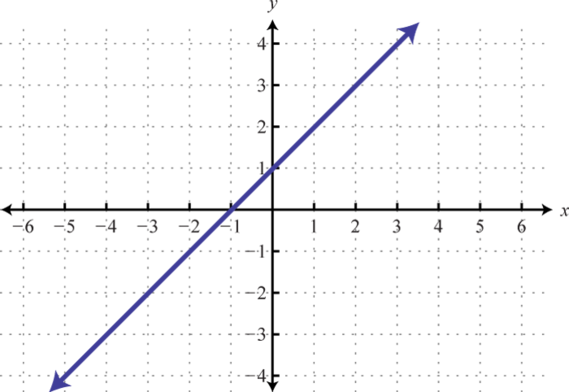
5.
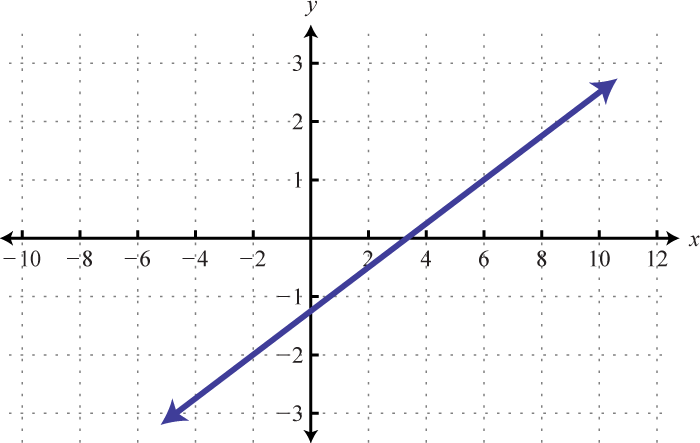
6.
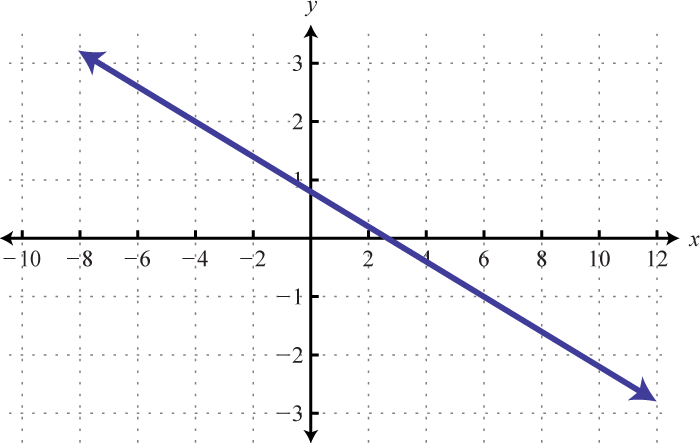
7.
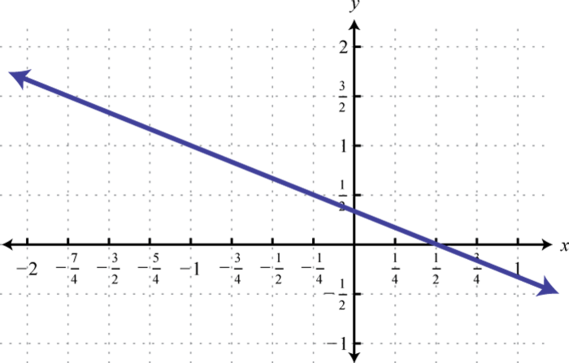
8.
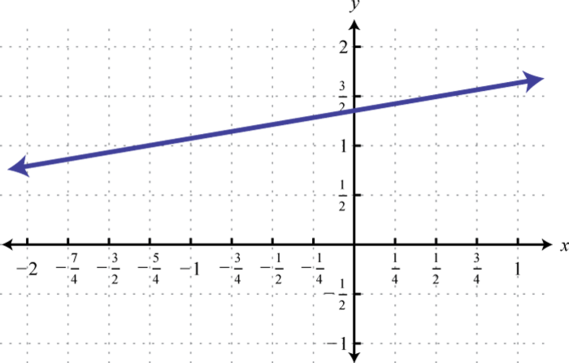
9.
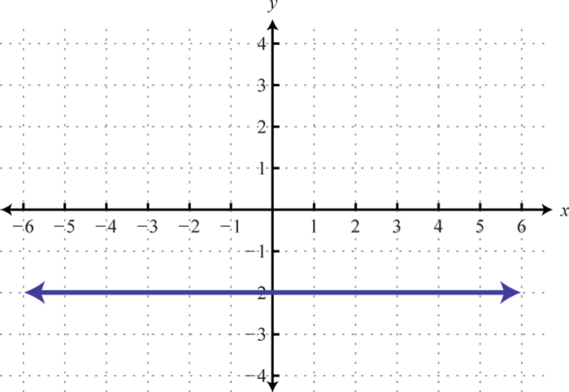
10.
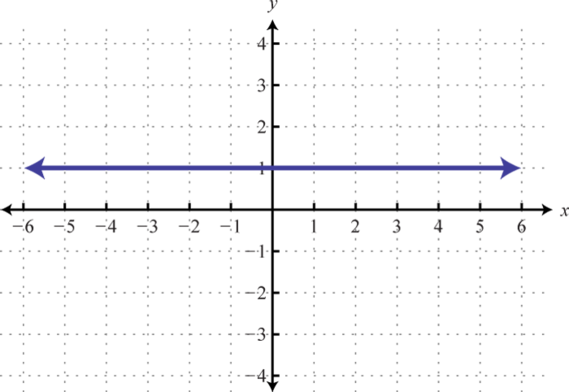
- Contestar
-
1. \(f (x) = − \frac{1}{2} x + \frac{1}{2}\)
3. \(f (x) = −x\)
5. \(f (x) = \frac{3}{8} x − \frac{5}{4}\)
7. \(f (x) = −\frac{2}{3} x + \frac{1}{3}\)
9. \(f (x) = −2\)
Ejercicio\(\PageIndex{5}\)
Encuentra la ecuación de la línea:
- Paralelo\(y = −\frac{5}{3}x +\frac{1}{2}\) y de paso\((−3, 4)\).
- Paralelo\(y = −\frac{3}{4}x −\frac{7}{3}\) y de paso\((−8, −1)\).
- Paralelo\(y = \frac{1}{3}x + 6\) y de paso\((2, −5)\).
- Paralelo\(y = \frac{1}{4}x + \frac{5}{3}\) y de paso\((5, 6)\).
- Paralelo\(4x − 5y = 15\) y de paso\((−1, −2)\).
- Paralelo\(3x − 4y = 2\) y de paso\((−6, 8)\).
- Paralelo\(2x + 12y = 9\) y de paso\((10, −9)\).
- Paralelo\(9x + 24y = 2\) y de paso\((−12, −4)\).
- Paralelo\(\frac{2}{15}x + \frac{1}{3}y = \frac{1}{10}\) y de paso\((−15, 4)\).
- Paralelo\(\frac{1}{3}x + \frac{2}{7}y = 1\) y de paso\((12, −11)\).
- Perpendicular a\(y = 5x + 2\) y de paso\((10, −5)\).
- Perpendicular a\(y = −2x + 1\) y de paso\((−8, −11)\).
- Perpendicular a\(y = \frac{3}{2}x − 5\) y de paso\((5, −3)\).
- Perpendicular a\(y = \frac{3}{4}x − \frac{1}{2}\) y de paso\((−6, −4)\).
- Perpendicular a\(12x + 15y = 3\) y de paso\((12, 15)\).
- Perpendicular a\(24x + 15y = 12\) y de paso\((2, −1)\).
- Perpendicular a\(14x − y = 3\) y de paso\((7, 3)\).
- Perpendicular a\(x − y = 4\) y de paso\((6, −2)\).
- Perpendicular a\(\frac{2}{15}x − \frac{3}{5}y = −1\) y de paso\((1, −1)\).
- Perpendicular a\(\frac{3}{4}x − \frac{2}{3}y = \frac{1}{2}\) y de paso\((−3, 6)\).
- Dar la ecuación de la línea que coincide con el\(x\) eje -eje.
- Dar la ecuación de la línea que coincide con el\(y\) eje -eje.
- Dada cualquier línea en forma estándar,\(ax + by = c\), determinar la pendiente de cualquier línea perpendicular.
- Dada cualquier línea en forma estándar,\(ax + by = c\), determinar la pendiente de cualquier línea paralela.
- Contestar
-
1. \(y = −\frac{5}{3}x − 1\)
3. \(y = \frac{1}{3}x − \frac{17}{3}\)
5. \(y = \frac{4}{5}x − \frac{6}{5}\)
7. \(y = −\frac{1}{6}x − \frac{22}{3}\)
9. \(y = −\frac{2}{5}x − 2\)
11. \(y = −\frac{1}{5}x − 3\)
13. \(y = −\frac{2}{3}x + \frac{1}{3}\)
15. \(y = \frac{5}{4}x\)
17. \(y = −\frac{1}{14}x + \frac{7}{2}\)
19. \(y = −\frac{9}{2}x + \frac{7}{2}\)
21. \(y = 0\)
23. \(m_{⊥} = \frac{b}{a}\)
Ejercicio\(\PageIndex{6}\)
Usa álgebra para resolver lo siguiente.
- Una empresa desea adquirir bolígrafos estampados con el logotipo de la empresa. Además de una tarifa de instalación inicial de\($90\), cada pluma cuesta\($1.35\) producir. Escribir una función que dé el costo en términos del número de bolígrafos producidos. Utilice la función para determinar el costo de producir\(500\) bolígrafos con el logotipo de la compañía estampado en él.
- Una compañía de alquiler de autos cobra una tarifa diaria de\($42.00\) más\($0.51\) por milla conducida. Escribe una función que dé el costo de rentar el auto por un día en cuanto al número de millas recorridas. Utilice la función para determinar el costo de rentar el auto por un día y conducirlo\(76\) millas.
- Un determinado plan de telefonía celular cobra\($16\) por mes y\($0.15\) por minuto de uso. Escribe una función que dé el costo del teléfono por mes en función del número de minutos de uso. Utilice la función para determinar el número de minutos de uso si la factura del primer mes fue\($46\).
- Una empresa de servicios web cobra\($2.50\) un mes más\($0.14\) por gigabyte de almacenamiento en su sistema. Escribir una función que dé el costo de almacenamiento por mes en términos del número de gigabytes almacenados. ¿Cuántos gigabytes se almacenan si la factura de este mes era\($6.00\)?
- Mary ha estado haciendo un seguimiento de sus facturas de teléfono celular durante los últimos dos meses. La factura del primer mes era\($45.00\) por\(150\) minutos de uso. La factura del segundo mes era\($25.00\) por\(50\) minutos de uso. Encuentra una función lineal que dé la factura mensual total en función de los minutos de uso.
- Una empresa en su primer año de negocios produjo\(1,200\) folletos por un costo total de\($5,050\). Al año siguiente, la compañía produjo\(500\) más folletos a un costo de\($2,250\). Utilice esta información para encontrar una función lineal que dé el costo total de producir folletos a partir del número de folletos producidos.
- Un Webmaster ha notado que el número de usuarios registrados ha ido en constante aumento desde que comenzó una campaña publicitaria. Antes de comenzar a anunciarse, tenía usuarios\(2,200\) registrados, y después de\(4\) meses de publicidad ahora tiene usuarios\(5,480\) registrados. Utilice estos datos para escribir una función lineal que dé el número total de usuarios registrados, dado el número de meses después de comenzar a publicitar. Utilice la función para predecir el número de usuarios\(8\) meses en la campaña publicitaria.
- Un granjero de maíz en California pudo producir\(154\) bushels de maíz por acre\(2\) años después de iniciar su operación. Actualmente, tras\(7\) años de operación, ha incrementado su rendimiento a\(164\) bushels por acre. Utilice esta información para escribir una función lineal que dé el rendimiento total por acre basado en el número de años de operación, y utilízala para predecir el rendimiento para el próximo año.
- Se compró una camioneta comercial nueva\($22,500\) y se espera que no tenga valor en\(12\) años. Utilice esta información para escribir una función de depreciación lineal para el valor de la camioneta. Utilizar la función para determinar el valor de la camioneta después de\(8\) años de uso.
- La vida útil promedio de un robot de soldadura industrial es de\(10\) años, después de lo cual se considera que no tiene valor. Si se compró un robot de soldadura industrial nuevo para\($58,000\), escriba una función que le dé el valor del robot en términos del número de años de operación. Utilice la función para valorar el robot después de\(3\) años de operación.
- Un negocio compró un equipo nuevo para\($2,400\). Después de\(5\) años de uso el equipo se valora en\($1,650\). Encuentre una función lineal que le dé el valor del equipo en términos de años de uso. Utilice la función para determinar el número de años después de los cuales la pieza del equipo no tendrá valor.
- Un vendedor gana un sueldo base de\($2,400\) un mes más un\(5\)% de comisión sobre todas las ventas. Escribir una función que dé el salario mensual del vendedor en términos de ventas. Utilice la función para determinar las ventas mensuales requeridas para ganar al menos\($3,600\) un mes.
- Cuando se contrató a cierto profesor en\(2005\), la matrícula en una universidad eran\(8,500\) estudiantes. Cinco años después, en\(2010\), la matrícula creció a\(11,200\) estudiantes. Determinar una función de crecimiento lineal que modele la población estudiantil en años posteriores\(2005\). Utilizar el modelo para predecir el año en el que la matrícula superará a\(13,000\) los alumnos.
- En\(1980\), la población de California era de alrededor de\(24\) un millón de personas. Veinte años después, en el año\(2000\), la población era de alrededor del\(34\) millón. Utilice estos datos para construir una función lineal que modele el crecimiento poblacional en años posteriores\(1980\). Utilizar la función para predecir el año en que la población alcanzará el\(40\) millón.
- Se compra un auto clásico\($24,500\) y se espera que aumente de valor cada año por\($672\). Escribir una función lineal que modele la apreciación del automóvil en términos del número de años posteriores a la compra. Utilice la función para predecir el valor del automóvil en\(7\) años.
- Una empresa reportó ventas en el primer y segundo trimestre de\($52,000\) y\($64,500\), respectivamente.
- Escribir una función lineal que modele las ventas del año en términos del trimestre\(n\).
- Utilice el modelo para predecir las ventas en el tercer y cuarto trimestre.
- Un motor de búsqueda en particular asigna un ranking a una página web en función del número de enlaces que dirigen a los usuarios a la página web. Si no se encuentran enlaces, a la página web se le asigna un ranking de\(1\). Si se encuentran\(20\) enlaces que dirigen a los usuarios a la página web, el buscador asigna un ranking de página de\(3.5\).
- Encuentra una función lineal que dé a la página web un ranking basado en el número de enlaces que dirigen a los usuarios hacia ella.
- ¿Cuántos enlaces serán necesarios para obtener un ranking de páginas de\(5\)?
- Las ventas en línea de un producto en particular están relacionadas con el número de clics en su anuncio. Se encontró que los\(1,520\) clics en un mes resultan en\($2,748\) ventas en línea, y que los\(1,840\) clics resultan en\($2,956\) ventas en línea. Escribir una función lineal que modele las ventas en línea del producto en función del número de clics en su anuncio. ¿Cuántos clics necesitaríamos esperar\($3,385\) en las ventas mensuales en línea de este producto en particular?
- Un negocio de fabricación de bicicletas puede producir\(x\) bicicletas a un costo, en dólares, dado por la fórmula\(C (x) = 85x + 2,400\). La empresa vende cada bicicleta a un precio mayorista de\($145\). El ingreso, en dólares, viene dado por\(R (x) = 145x\), donde\(x\) representa el número de bicicletas vendidas. Escribir una función que dé ganancias en cuanto al número de bicicletas producidas y vendidas. Utilice la función para determinar el número de bicicletas que necesitan ser producidas y vendidas para alcanzar el punto de equilibrio.
- El costo, en dólares, de producir lámparas\(n\) personalizadas viene dado por la fórmula\(C (n) = 28n + 360\). Cada lámpara se puede vender en línea para\($79\). El ingreso en dólares, viene dado por\(R (n) = 79n\), donde\(n\) representa el número de lámparas vendidas. Escribir una función que dé el beneficio de producir y vender lámparas\(n\) personalizadas. Utilice la función para determinar cuántas lámparas se deben producir y vender para obtener al menos\($1,000\) ganancias.
- Un fabricante puede producir un juego de mesa a un costo de\($12\) por unidad después de una inversión inicial fija de reutillaje de\($12,500\). Los juegos se pueden vender por\($22\) cada uno a minoristas.
- Escribe una función que dé los costos de fabricación cuando se producen\(n\) juegos.
- Escribir una función que dé los ingresos de la venta de\(n\) juegos a los minoristas.
- Escribir una función que dé el beneficio de producir y vender\(n\) unidades.
- ¿Cuántas unidades se deben vender para obtener una ganancia de al menos\($37,500\)?
- Una máquina expendedora se puede arrendar a un\($90\) costo mensual. Los artículos utilizados para almacenar la máquina pueden ser comprados por\($0.50\) cada uno y vendidos para\($1.25\) cada uno.
- Escribir una función que dé el costo mensual de arrendamiento y almacenamiento de la máquina expendedora con\(n\) artículos.
- Escribir una función que dé los ingresos generados por la venta de\(n\) artículos.
- Escribir una función que dé el beneficio de almacenar y vender\(n\) artículos por mes.
- ¿Cuántos artículos deben venderse cada mes para alcanzar el punto de equilibrio?
- Contestar
-
1. \(C ( x ) = 1.35 x + 90 ; \$ 765\)
3. \(C ( x ) = 0.15 x + 16 ;\: 200 \:\text{minutes}\)
5. \(C ( x ) = 0.20 x + 15\)
7. \(U ( x ) = 820 x + 2,200 \:; 8,760 \: \text{users}\)
9. \(V ( t ) = - 1,875 t + 22,500 ;\: \$ 7,500\)
11. \(V ( t ) = - 150 t + 2,400\: ; 16\: \text{years}\)
13. \(P ( x ) = 540 x + 8,500 ;\: 2013\)
15. \(V ( t ) = 672 t + 24,500 ;\: \$ 29,204\)
17. (1)\(r ( n ) = 0.125 n + 1\); (2)\(32\) enlaces
19. \(P ( x ) = 60 x - 2,400\: ; 40\:\text{bicycles}\)
21. (1)\(C ( n ) = 12 n + 12,500\); (2)\(R ( n ) = 22 n\); (3)\(P ( n ) = 10 n - 12,500\); (4) al menos\(5,000\) unidades
Ejercicio\(\PageIndex{1}\)
- Investigar y discutir la depreciación lineal. En un modelo de depreciación lineal, ¿qué representan la pendiente y la\(y\) intercepción?
- Anota tus propios pasos para encontrar la ecuación de una línea. Publica tus pasos en el panel de discusión.
- Contestar
-
1. La respuesta puede variar
Notas al pie
30 Cualquier línea no vertical se puede escribir en la forma\(y − y_{1} = m (x − x_{1} )\), donde\(m\) está la pendiente y\((x_{1} , y_{1} )\) es cualquier punto de la línea.
31 Líneas en un mismo plano que no se cruzan; sus pendientes son las mismas.
32 Líneas en un mismo plano que se cruzan en ángulo recto; sus pendientes son recíprocas opuestas.
33 Se utiliza cuando se refiere a recíprocos opuestos.
34 Dos números reales cuyo producto es\(−1\). Dado un número real\(\frac{a}{b}\), lo recíproco opuesto es\(−\frac{b}{a}\).
35 Usar datos para encontrar ecuaciones matemáticas que describan, o modelen, aplicaciones del mundo real.
36 Función lineal utilizada para describir el valor decreciente de un ítem a lo largo del tiempo.
37 Usar una función lineal para estimar un valor entre puntos de datos dados.
38 Usar una función lineal para estimar valores que se extienden más allá de los puntos de datos dados.
39 Una función que modela los ingresos en función de un número de unidades vendidas.
40 Una función que modela el costo de producir un número de unidades.
41 Una función que modela el beneficio como ingresos menos costo.
42 El punto en el que la ganancia no es ni negativa ni positiva; la ganancia es igual a cero.


