2.6: Resolver ecuaciones de valores absolutos y desigualdades

Objetivos de aprendizaje

• Revisar la definición de valor absoluto.
• Resolver ecuaciones de valor absoluto.
• Resolver desigualdades de valor absoluto.

Ecuaciones de Valor Absoluto

Recordemos que el valor absoluto ⁶³ de un número real\(a\), denotado\(|a|\), se define como la distancia entre cero (el origen) y la gráfica de ese número real en la recta numérica. Por ejemplo,\(|−3|=3\) y\(|3|=3\).

Figura\(\PageIndex{1}\)

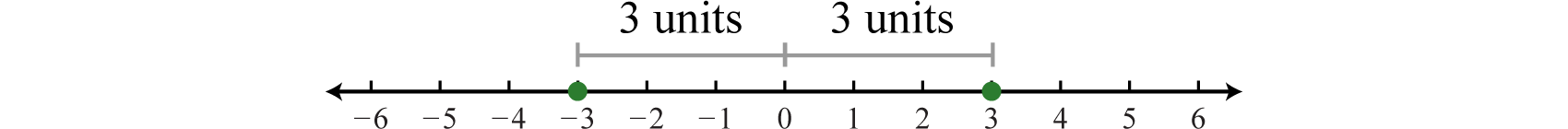
Además, el valor absoluto de un número real puede definirse algebraicamente como una función por partes.

\(| a | = \left\{ \begin{array} { l } { a \text { if } a \geq 0 } \\ { - a \text { if } a < 0 } \end{array} \right.\)

Dada esta definición,\(|3| = 3\) y\(|−3| = − (−3) = 3\) .Por lo tanto, la ecuación\(|x| = 3\) tiene dos soluciones para\(x\), a saber\(\{±3\}\). En general, dada cualquier expresión algebraica\(X\) y cualquier número positivo\(p\):

\(\text{If}\: | X | = p \text { then } X = - p \text { or } X = p\)

Es decir, el argumento del valor absoluto ⁶⁴\(X\) puede ser positivo o negativo\(p\). Utilice este teorema para resolver ecuaciones de valor absoluto algebraicamente.

Ejemplo\(\PageIndex{1}\):

Resolver:\(|x+2|=3\).

Solución

En este caso, el argumento del valor absoluto es\(x+2\) y debe ser igual a\(3\) o\(−3\).

Figura\(\PageIndex{2}\)

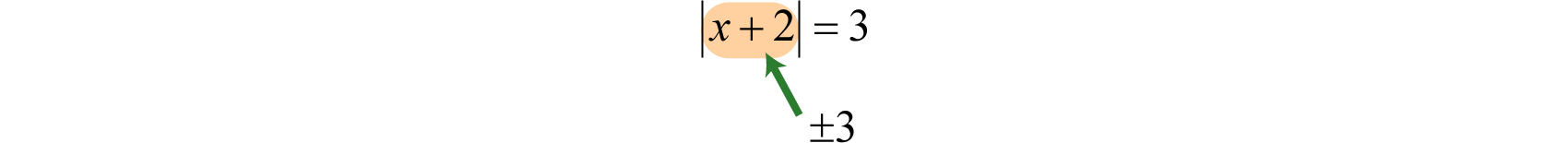
Por lo tanto, para resolver esta ecuación de valor absoluto, establecer\(x+2\) igual a\(±3\) y resolver cada ecuación lineal como de costumbre.

\(\begin{array} { c } { | x + 2 | = 3 } \\ { x + 2 = - 3 \quad \quad\text { or } \quad\quad x + 2 = 3 } \\ { x = - 5 \quad\quad\quad\quad\quad\quad\quad x = 1 } \end{array}\)

Respuesta:

Las soluciones son\(−5\) y\(1\).

Para visualizar estas soluciones, grafica las funciones a cada lado del signo igual en el mismo conjunto de ejes de coordenadas. En este caso,\(f (x) = |x + 2|\) es una función de valor absoluto desplazada dos unidades horizontalmente hacia la izquierda, y\(g (x) = 3\) es una función constante cuya gráfica es una línea horizontal. Determinar los\(x\) -valores donde\(f (x) = g (x)\).

Figura\(\PageIndex{3}\)

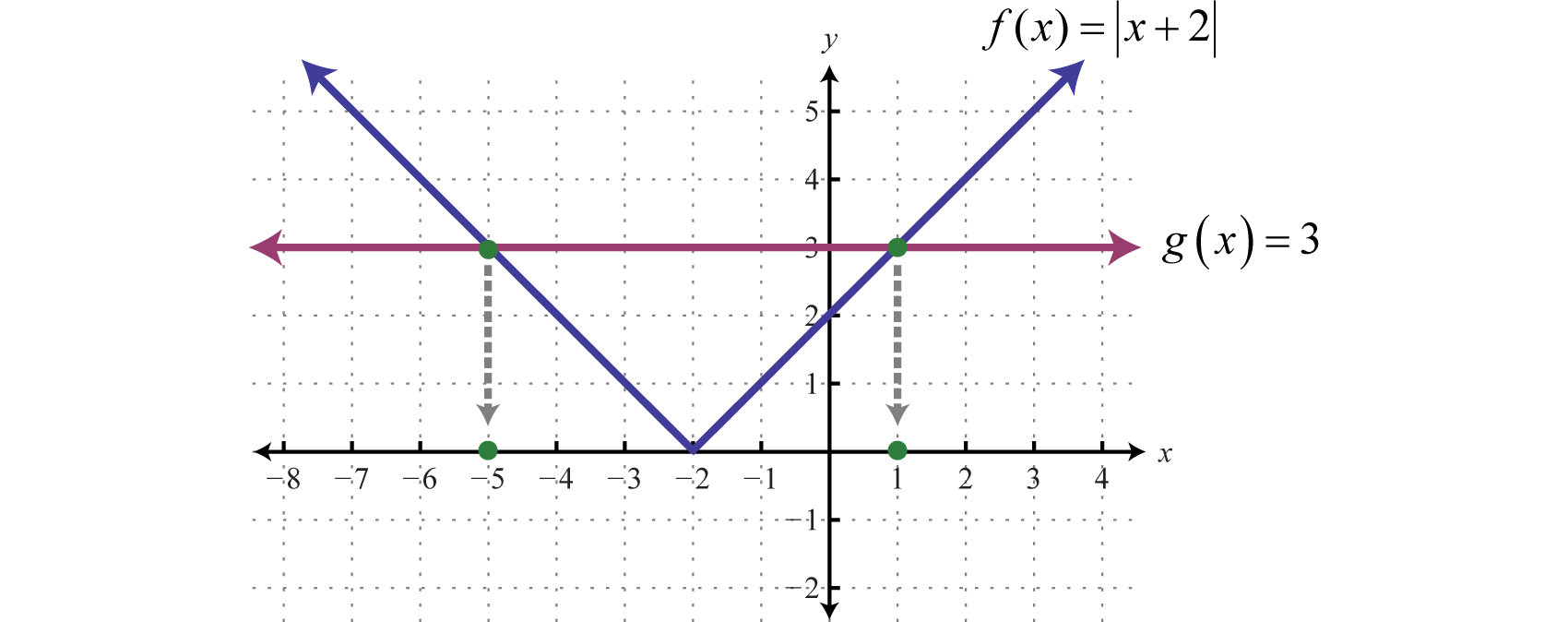
De la gráfica podemos ver que ambas funciones coinciden donde\(x = −5\) y\(x = 1\). Las soluciones corresponden a los puntos de intersección.

Ejemplo\(\PageIndex{2}\):

Resolver:\(| 2 x + 3 | = 4\).

Solución

Aquí el argumento del valor absoluto es\(2x+3\) y puede ser igual a\(-4\) o\(4\).

\(\begin{array} { r l } { | 2 x + 3 | } & { = \quad 4 } \\ { 2 x + 3 = - 4 } & { \text { or }\quad 2 x + 3 = 4 } \\ { 2 x = - 7 } & \quad\quad\:\: { 2 x = 1 } \\ { x = - \frac { 7 } { 2 } } & \quad\quad\:\: { x = \frac { 1 } { 2 } } \end{array}\)

Verifique si estas soluciones satisfacen la ecuación original.

Mesa\(\PageIndex{1}\)

Comprobar\(x=-\frac{7}{2}\)	Comprobar\(x=\frac{1}{2}\)
\(\begin{aligned} | 2 x + 3 | & = 4 \\ \left| 2 \left( \color{Cerulean}{- \frac { 7 } { 2 }} \right) + 3 \right| & = 4 \\ | - 7 + 3 | & = 4 \\ | - 4 | & = 4 \\ 4 & = 4 \:\:\color{Cerulean}{✓} \end{aligned}\)	\(\begin{array} { r } { | 2 x + 3 | = 4 } \\ { \left| 2 \left( \color{Cerulean}{\frac { 1 } { 2 }} \right) + 3 \right| = 4 } \\ { | 1 + 3 | = 4 } \\ { | 4 | = 4 } \\ { 4 = 4 } \:\:\color{Cerulean}{✓} \end{array}\)

Respuesta:

Las soluciones son\(-\frac{7}{2}\) y\(\frac{1}{2}\).

Para aplicar el teorema, se debe aislar el valor absoluto. Los pasos generales para resolver ecuaciones de valor absoluto se describen en el siguiente ejemplo.

Ejemplo\(\PageIndex{3}\):

Resolver:\(2 |5x − 1| − 3 = 9\).

Solución

Paso 1: Aísle el valor absoluto para obtener el formulario\(|X| = p\).

\(\begin{aligned} 2 | 5 x - 1 | - 3 & = 9 \:\:\:\color{Cerulean} { Add\: 3\: to\: both\: sides. } \\ 2 | 5 x - 1 | & = 12 \:\:\color{Cerulean} { Divide\: both\: sides\: by\: 2 } \\ | 5 x - 1 | & = 6 \end{aligned}\)

Paso 2: Establecer el argumento del valor absoluto igual a\(±p\). Aquí el argumento es\(5x − 1\) y\(p = 6\).

\(5 x - 1 = - 6 \text { or } 5 x - 1 = 6\)

Paso 3: Resuelve cada una de las ecuaciones lineales resultantes.

\(\begin{array} { r l } { 5 x - 1 = - 6 \quad\:\:\text { or } \quad\quad5 x - 1 } & { \:\:\:\:\:\:= 6 } \\ { 5 x = - 5 }\quad\:\quad\quad\quad\quad\quad\quad\: & { 5 x = 7 } \\ { x = - 1 } \quad\quad\quad\quad\quad\quad\quad\:\:& { x = \frac { 7 } { 5 } } \end{array}\)

Paso 4: Verificar las soluciones en la ecuación original.

Mesa\(\PageIndex{2}\)

Comprobar\(x=-1\)	Comprobar\(x=\frac{7}{5}\)
\(\begin{aligned} 2 | 5 x - 1 | - 3 & = 9 \\ 2 | 5 ( \color{Cerulean}{- 1}\color{Black}{ )} - 1 | - 3 & = 9 \\ 2 | - 5 - 1 | - 3 & = 9 \\ 2 | - 6 | - 3 & = 9 \\ 12 - 3 & = 9 \\ 9 & = 9 \color{Cerulean}{✓}\end{aligned}\)	\(\begin{aligned} 2 | 5 x - 1 | - 3 & = 9 \\ 2 \left| 5 \left( \color{Cerulean}{\frac { 7 } { 5 }} \right) - 1 \right| - 3 & = 9 \\ 2 | 7 - 1 | - 3 & = 9 \\ 2 | 6 | - 3 & = 9 \\ 12 - 3 & = 9 \\ 9 & = 9 \color{Cerulean}{✓} \end{aligned}\)

Respuesta:

Las soluciones son\(-1\) y\(\frac{7}{5}\)

Ejercicio\(\PageIndex{1}\)

Resolver:\(2 - 7 | x + 4 | = - 12\).

Contestar

\(-6, -2\)

www.youtube.com/v/g0eJbqreymu

No todas las ecuaciones de valor absoluto tendrán dos soluciones.

Ejemplo\(\PageIndex{4}\):

Resolver:\(| 7 x - 6 | + 3 = 3\).

Solución

Comience aislando el valor absoluto.

\(\begin{array} { l } { | 7 x - 6 | + 3 = 3 \:\:\:\color{Cerulean} { Subtract\: 3\: on\: both\: sides.} } \\ { \quad | 7 x - 6 | = 0 } \end{array}\)

Sólo cero tiene el valor absoluto de cero,\(|0| = 0\). En otras palabras,\(|X| = 0\) tiene una solución, a saber\(X = 0\). Por lo tanto, establecer el argumento\(7x − 6\) igual a cero y luego resolver para\(x\).

\(\begin{aligned} 7 x - 6 & = 0 \\ 7 x & = 6 \\ x & = \frac { 6 } { 7 } \end{aligned}\)

Geométricamente, una solución corresponde a un punto de intersección.

Figura\(\PageIndex{4}\)

Respuesta:

La solución es\(\frac{6}{7}\).

Ejemplo\(\PageIndex{5}\):

Resolver:\(|x+7|+5=4\).

Solución

Comience aislando el valor absoluto.

\(\begin{aligned} | x + 7 | + 5 & = 4 \:\:\color{Cerulean} { Subtract \: 5\: on\: both\: sides.} \\ | x + 7 | & = - 1 \end{aligned}\)

En este caso, podemos ver que el valor absoluto aislado es igual a un número negativo. Recordemos que el valor absoluto siempre será positivo. Por lo tanto, concluimos que no hay solución. Geométricamente, no hay punto de intersección.

Figura\(\PageIndex{5}\)

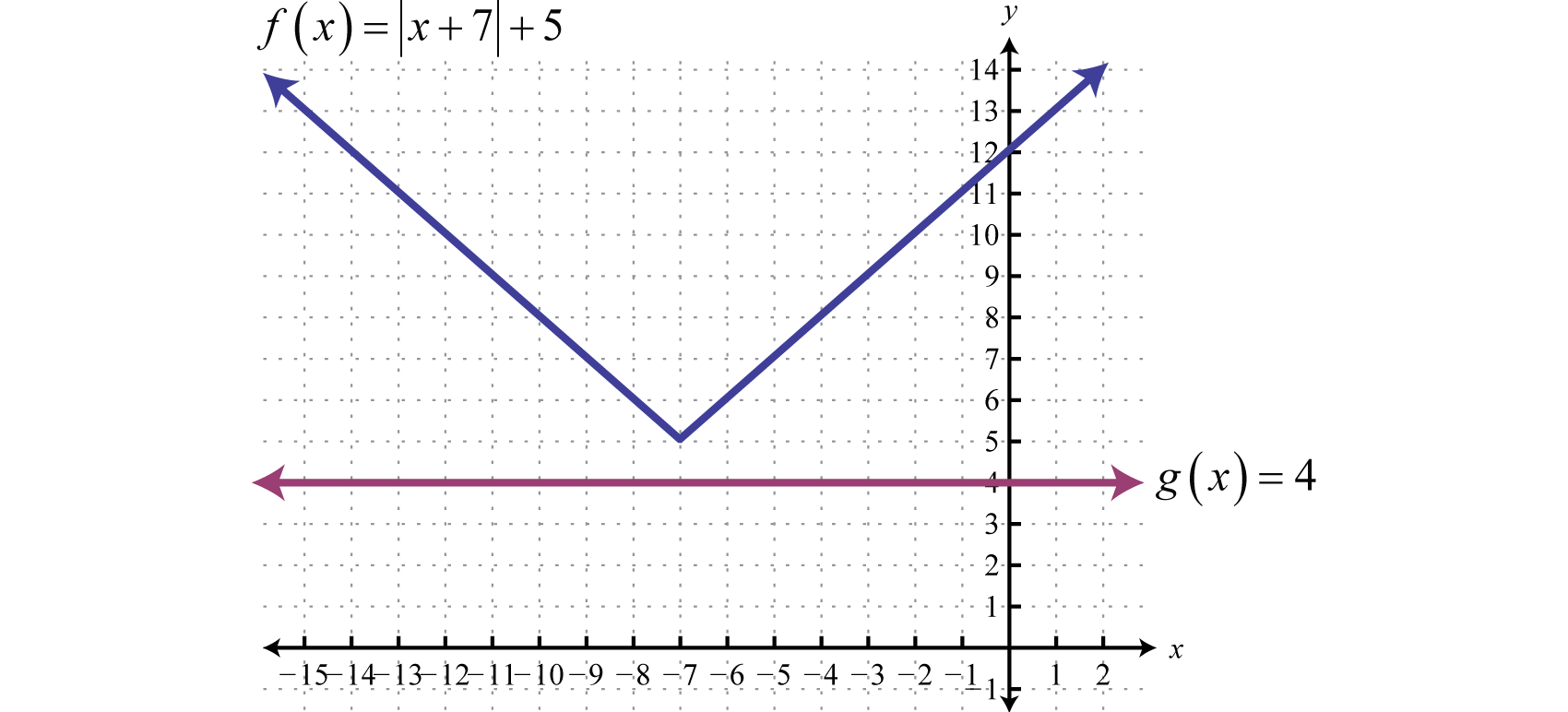
Respuesta:

No hay solución,\(Ø\).

Si se le da una ecuación con dos valores absolutos de la forma\(| a | = | b |\), entonces\(b\) debe ser igual\(a\) o opuesto. Por ejemplo, si\(a=5\), entonces\(b = \pm 5\) y tenemos:

\(| 5 | = | - 5 | \text { or } | 5 | = | + 5 |\)

En general, dadas las expresiones algebraicas\(X\) y\(Y\):

\(\text{If} | X | = | Y | \text { then } X = - Y \text { or } X = Y\).

En otras palabras, si dos expresiones de valor absoluto son iguales, entonces los argumentos pueden ser iguales u opuestos.

Ejemplo\(\PageIndex{6}\):

Resolver:\(| 2 x - 5 | = | x - 4 |\).

Solución

Establezca\(2x-5\) igual a\(\pm ( x - 4 )\) y luego resuelva cada ecuación lineal.

\(\begin{array} { c } { | 2 x - 5 | = | x - 4 | } \\ { 2 x - 5 = - ( x - 4 ) \:\: \text { or }\:\: 2 x - 5 = + ( x - 4 ) } \\ { 2 x - 5 = - x + 4 }\quad\quad\quad 2x-5=x-4 \\ { 3 x = 9 }\quad\quad\quad\quad\quad\quad \quad\quad x=1 \\ { x = 3 \quad\quad\quad\quad\quad\quad\quad\quad\quad\:\:\:\:} \end{array}\)

Para verificar, sustituimos estos valores en la ecuación original.

Mesa\(\PageIndex{3}\)

Comprobar\(x=1\)	Comprobar\(x=3\)
\(\begin{aligned} | 2 x - 5 | & = | x - 4 | \\ | 2 ( \color{Cerulean}{1}\color{Black}{ )} - 5 | & = | ( \color{Cerulean}{1}\color{Black}{ )} - 4 | \\ | - 3 | & = | - 3 | \\ 3 & = 3 \color{Cerulean}{ ✓}\end{aligned}\)	\(\begin{aligned} | 2 x - 5 | & = | x - 4 | \\ | 2 ( \color{Cerulean}{3}\color{Black}{ )} - 5 | & = | ( \color{Cerulean}{3}\color{Black}{ )} - 4 | \\ | 1 | & = | - 1 | \\ 1 & = 1 \color{Cerulean}{✓}\end{aligned}\)

Como ejercicio, use una utilidad gráfica para graficar ambos\(f(x)= |2x-5|\) y\(g(x)=|x-4|\) en el mismo conjunto de ejes. Verifique que las gráficas se crucen donde\(x\) es igual a\(1\) y\(3\).

Respuesta:

Las soluciones son\(1\) y\(3\).

Ejercicio\(\PageIndex{2}\)

Resolver:\(| x + 10 | = | 3 x - 2 |\).

Contestar

\(-2, 6\)

www.youtube.com/v/cskwmsqcbmu

Desigualdades de valor absoluto

Comenzamos por examinar las soluciones a la siguiente desigualdad:

\(| x | \leq 3\)

El valor absoluto de un número representa la distancia desde el origen. Por lo tanto, esta ecuación describe todos los números cuya distancia desde cero es menor o igual a\(3\). Podemos graficar este conjunto de soluciones sombreando todos esos números.

Figura\(\PageIndex{6}\)

Ciertamente podemos ver que hay infinitamente muchas soluciones para\(|x|≤3\) delimitar por\(−3\) y\(3\). Exprese este conjunto de soluciones usando notación de conjunto o notación de intervalo de la siguiente manera

\(\begin{array} { c } { \{ x | - 3 \leq x \leq 3 \} \color{Cerulean} { Set\: Notation } } \\ { [ - 3,3 ] \quad \color{Cerulean}{ Interval \:Notation } } \end{array}\)

En este texto, optaremos por expresar soluciones en notación de intervalos. En general, dada cualquier expresión algebraica\(X\) y cualquier número positivo\(p\):

\(\text{If} | X | \leq p \text { then } - p \leq X \leq p\).

Este teorema también es válido para las desigualdades estrictas. En otras palabras, podemos convertir cualquier desigualdad de valor absoluto que implique "menos que" en una desigualdad compuesta que pueda resolverse como de costumbre.

Ejemplo\(\PageIndex{7}\):

Resuelve y grafica el conjunto de soluciones:\(|x+2|<3\).

Solución

Encuadernado el argumento\(x+2\) por\(−3\)\(3\) y y resolver.

\(\begin{array} { c } { | x + 2 | < 3 } \\ { - 3 < x + 2 < 3 } \\ { - 3 \color{Cerulean}{- 2}\color{Black}{ <} x + 2 \color{Cerulean}{- 2}\color{Black}{ <} 3 \color{Cerulean}{- 2} } \\ { - 5 < x < 1 } \end{array}\)

Aquí utilizamos puntos abiertos para indicar desigualdades estrictas en la gráfica de la siguiente manera.

Figura\(\PageIndex{7}\)

Respuesta:

Usando notación de intervalos,\((−5,1)\).

La solución a se\(| x + 2 | < 3\) puede interpretar gráficamente si dejamos\(f ( x ) = | x + 2 |\)\(g(x)=3\) y luego determinar dónde\(f ( x ) < g ( x )\) graficando ambos\(f\) y\(g\) sobre el mismo conjunto de ejes.

Figura\(\PageIndex{7}\)

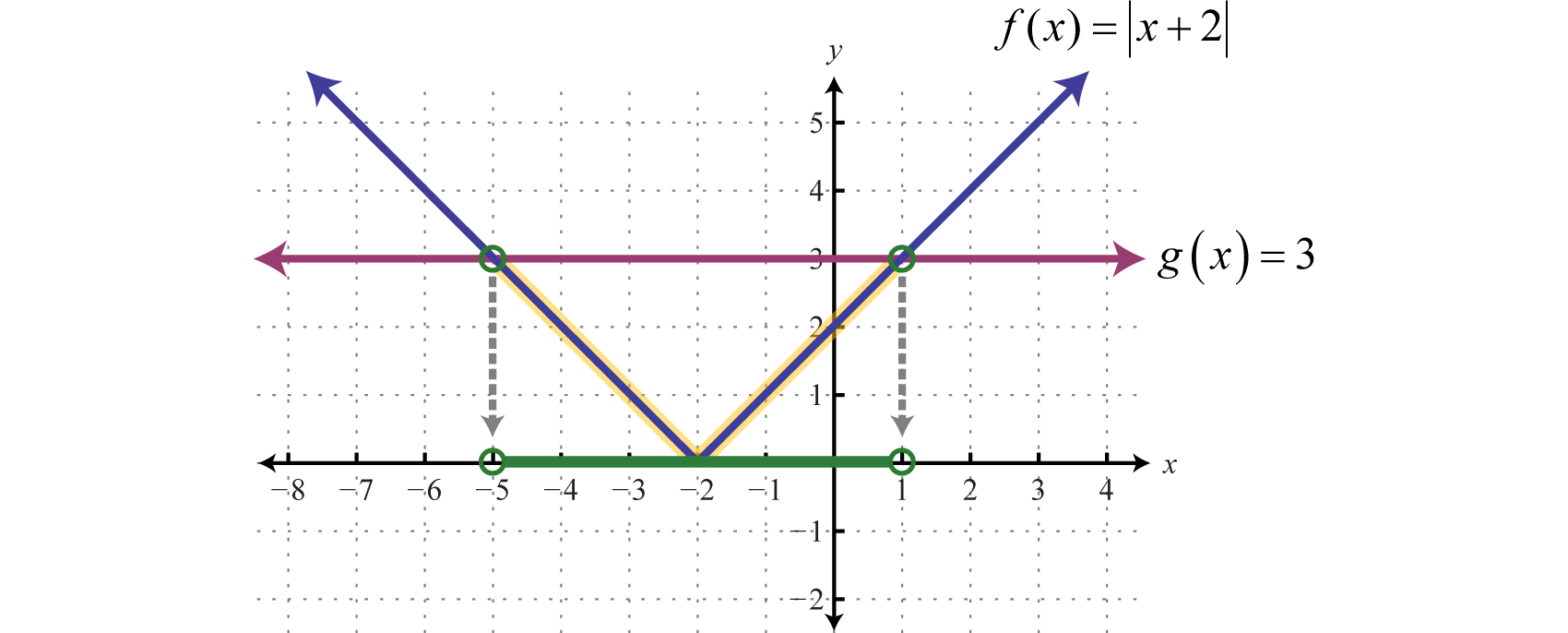
La solución consiste en todos los\(x\) -valores donde la gráfica de\(f\) está por debajo de la gráfica de\(g\). En este caso, podemos ver que\(|x + 2| < 3\) donde están los\(x\) -valores entre\(−5\) y\(1\). Para aplicar el teorema, primero debemos aislar el valor absoluto.

Ejemplo\(\PageIndex{8}\):

Resolver:\(4 |x + 3| − 7 ≤ 5\).

Solución

Comience aislando el valor absoluto.

\(\begin{array} { c } { 4 | x + 3 | - 7 \leq 5 } \\ { 4 | x + 3 | \leq 12 } \\ { | x + 3 | \leq 3 } \end{array}\)

A continuación, aplicar el teorema y reescribir la desigualdad de valor absoluto como una desigualdad compuesta.

\(\begin{array} { c } { | x + 3 | \leq 3 } \\ { - 3 \leq x + 3 \leq 3 } \end{array}\)

Resolver.

\(\begin{aligned} - 3 \leq x + 3 \leq & 3 \\ - 3 \color{Cerulean}{- 3} \color{Black}{ \leq} x + 3 \color{Cerulean}{- 3} & \color{Black}{ \leq} 3 \color{Cerulean}{- 3} \\ - 6 \leq x \leq 0 \end{aligned}\)

Sombra las soluciones en una recta numérica y presente la respuesta en notación de intervalos. Aquí utilizamos puntos cerrados para indicar desigualdades inclusivas en la gráfica de la siguiente manera:

Figura\(\PageIndex{8}\)

Respuesta:

Usando la notación de intervalos,\([−6,0]\)

Ejercicio\(\PageIndex{3}\)

Resuelve y grafica el conjunto de soluciones:\(3 + | 4 x - 5 | < 8\).

Contestar

Notación de intervalos:\((0, \frac{5}{2})\)

Figura\(\PageIndex{9}\)

www.youtube.com/V/SX6PPL2FBQ0

A continuación, examinamos las soluciones a una desigualdad que implica "mayor que”, como en el siguiente ejemplo:

\(| x | \geq 3\)

Esta desigualdad describe todos los números cuya distancia desde el origen es mayor o igual a\(3\). En una gráfica, podemos sombrear todos esos números.

Figura\(\PageIndex{10}\)

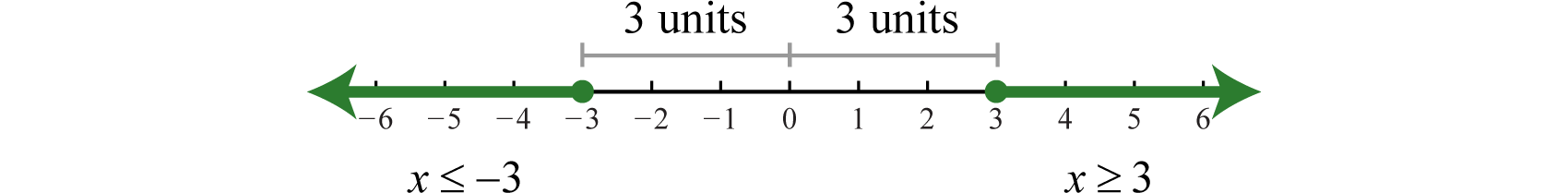
Hay infinitamente muchas soluciones que se pueden expresar usando notación de conjuntos y notación de intervalos de la siguiente manera:

\(\begin{array} { l } { \{ x | x \leq - 3 \text { or } x \geq 3 \} \:\:\color{Cerulean} { Set\: Notation } } \\ { ( - \infty , - 3 ] \cup [ 3 , \infty ) \:\:\color{Cerulean} { Interval\: Notation } } \end{array}\)

En general, dada cualquier expresión algebraica\(X\) y cualquier número positivo\(p\):

\(\text{If} | X | \geq p \text { then } X \leq - p \text { or } X \geq p\).

El teorema también es válido para las desigualdades estrictas. En otras palabras, podemos convertir cualquier desigualdad de valor absoluto que implique “mayor que” en una desigualdad compuesta que describa dos intervalos.

Ejemplo\(\PageIndex{9}\):

Resuelve y grafica el conjunto de soluciones:\(|x+2|>3\).

Solución

El argumento\(x+2\) debe ser menor\(−3\) o mayor que\(3\).

\(\begin{array} { c } { | x + 2 | > 3 } \\ { x + 2 < - 3 \quad \text { or } \quad x + 2 > 3 } \\ { x < - 5 }\quad\quad\quad\quad\quad\: x>1 \end{array}\)

Figura\(\PageIndex{11}\)

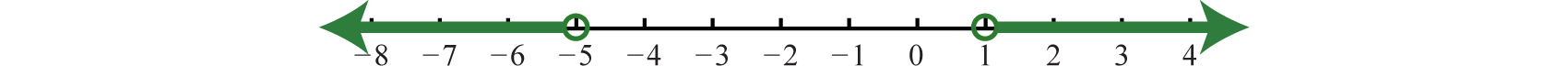
Respuesta:

Usando notación de intervalos,\((−∞,−5)∪(1,∞)\).

La solución a se\(|x + 2| > 3\) puede interpretar gráficamente si dejamos\(f (x) = |x + 2|\)\(g (x) = 3\) y luego determinar dónde\(f(x) > g (x)\) graficando ambos\(f\) y\(g\) sobre el mismo conjunto de ejes.

Figura\(\PageIndex{12}\)

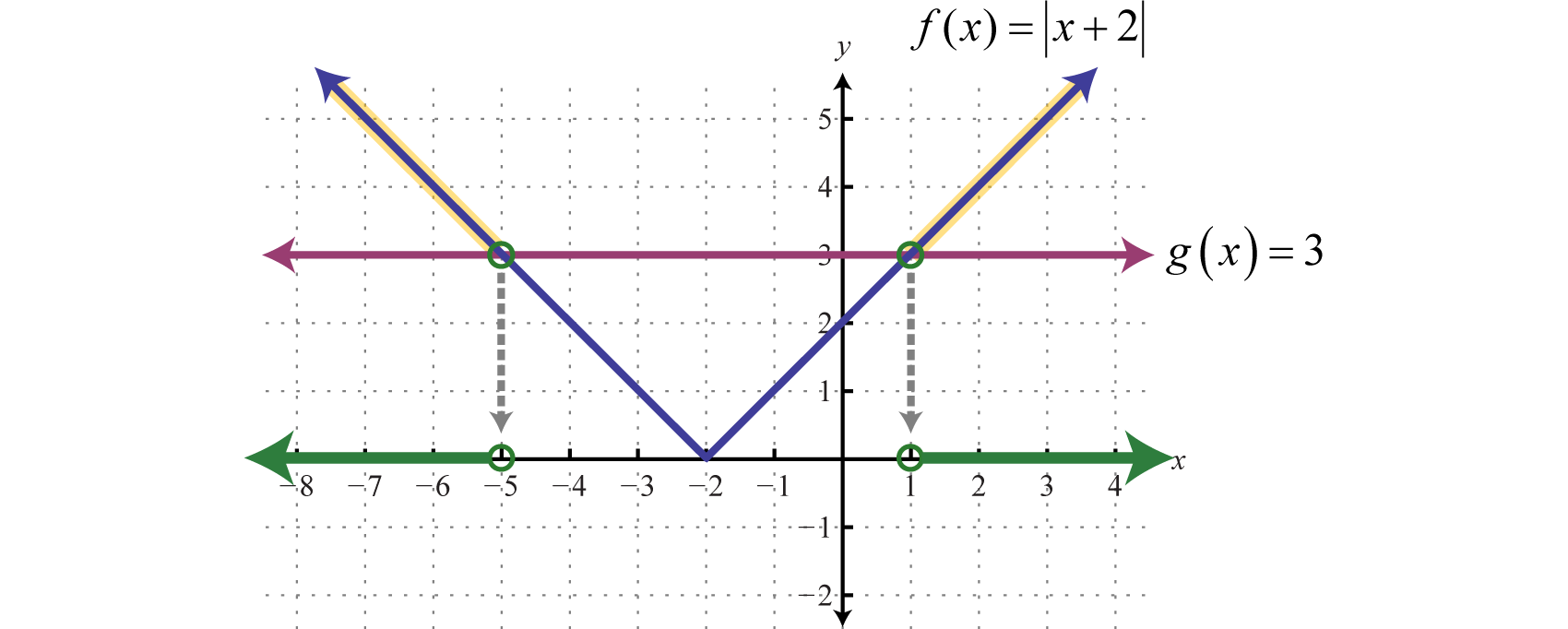
La solución consiste en todos los\(x\) -valores donde la gráfica de\(f\) está por encima de la gráfica de\(g\). En este caso, podemos ver que\(|x + 2| > 3\) donde los\(x\) -valores son menores que\(−5\) o son mayores que\(1\). Para aplicar el teorema primero debemos aislar el valor absoluto.

Ejemplo\(\PageIndex{10}\):

Resolver:\(3 + 2 |4x − 7| ≥ 13\).

Solución

Comience aislando el valor absoluto.

\(\begin{array} { r } { 3 + 2 | 4 x - 7 | \geq 13 } \\ { 2 | 4 x - 7 | \geq 10 } \\ { | 4 x - 7 | \geq 5 } \end{array}\)

A continuación, aplicar el teorema y reescribir la desigualdad de valor absoluto como una desigualdad compuesta.

\(\begin{array} &\quad\quad\quad\quad\:\:\:|4x-7|\geq 5 \\ 4 x - 7 \leq - 5 \quad \text { or } \quad 4 x - 7 \geq 5 \end{array}\)

Resolver.

\(\begin{array} { l } { 4 x - 7 \leq - 5 \text { or } 4 x - 7 \geq 5 } \\ \quad\:\:\:\:{ 4 x \leq 2 } \quad\quad\quad\:\:\: 4x\geq 12\\ \quad\:\:\:\:{ 4 x \leq \frac { 2 } { 4 } } \quad\quad\quad\quad x\geq 3 \\ \quad\quad{ 4 x \leq \frac { 1 } { 2 } } \end{array}\)

Sombra las soluciones en una recta numérica y presente la respuesta usando notación de intervalo.

Figura\(\PageIndex{13}\)

Respuesta:

Usando la notación de intervalos,\((−∞,12]∪[3,∞)\)

Ejercicio\(\PageIndex{4}\)

Resolver y graficar:\(3 | 6 x + 5 | - 2 > 13\).

Contestar

Usando la notación de intervalos,\(\left( - \infty , - \frac { 5 } { 3 } \right) \cup ( 0 , \infty )\)

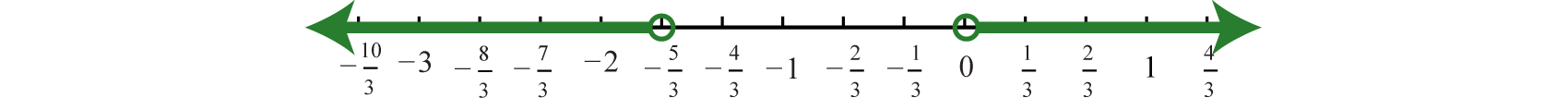
Figura\(\PageIndex{14}\)

www.youtube.com/v/p6hjrz6w4f4

Hasta este punto, los conjuntos de soluciones de desigualdades lineales de valores absolutos han consistido en un solo intervalo delimitado o dos intervalos no acotados. No siempre es así.

Ejemplo\(\PageIndex{11}\):

Resolver y graficar:\(|2x−1|+5>2\).

Solución

Comience aislando el valor absoluto.

\(\begin{array} { c } { | 2 x - 1 | + 5 > 2 } \\ { | 2 x - 1 | > - 3 } \end{array}\)

Observe que tenemos un valor absoluto mayor que un número negativo. Para cualquier número real x el valor absoluto del argumento siempre será positivo. De ahí que cualquier número real resolverá esta desigualdad.

Figura\(\PageIndex{15}\)

Geométricamente, podemos ver que siempre\(f(x)=|2x−1|+5\) es mayor que\(g(x)=2\).

Figura\(\PageIndex{16}\)

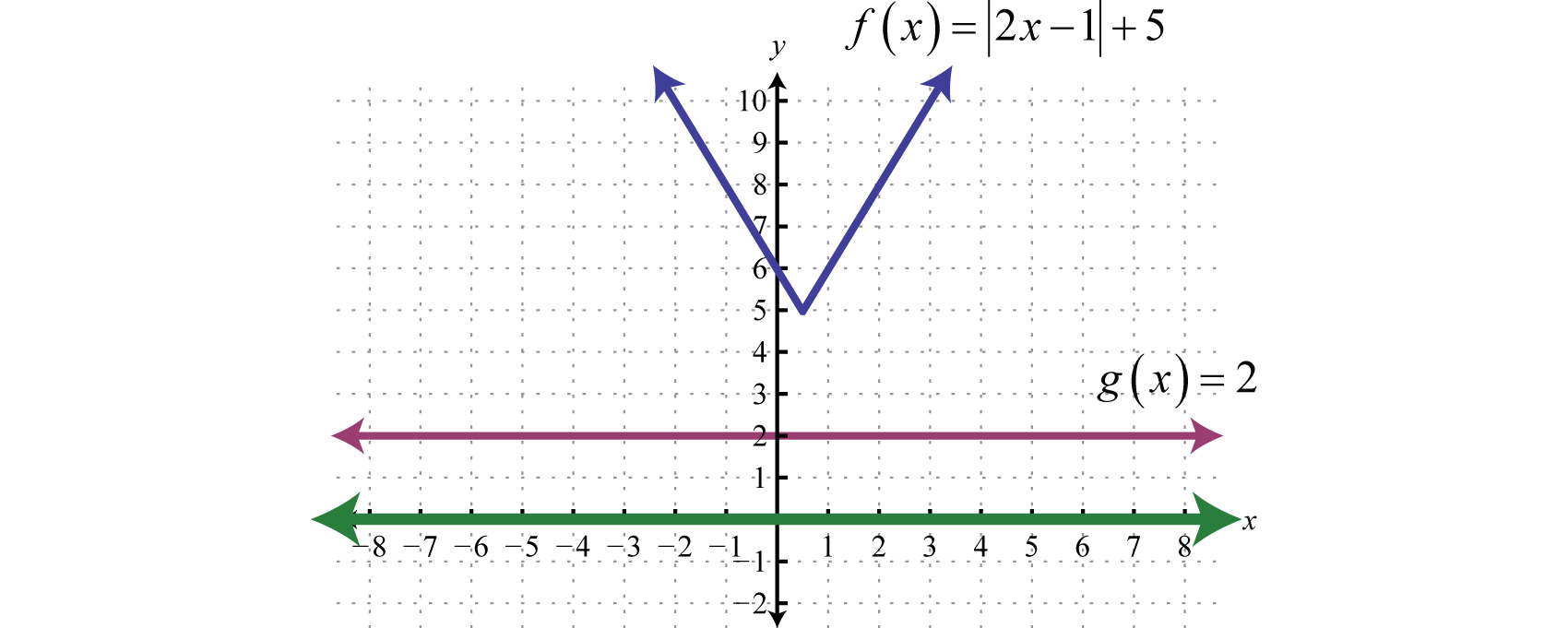
Respuesta:

Todos los números reales,\(ℝ\).

Ejemplo\(\PageIndex{12}\):

Resolver y graficar:\(|x+1|+4≤3\).

Solución

Comience aislando el valor absoluto.

\(\begin{array} { l } { | x + 1 | + 4 \leq 3 } \\ { | x + 1 | \leq - 1 } \end{array}\)

En este caso, podemos ver que el valor absoluto aislado es ser menor o igual que un número negativo. Nuevamente, el valor absoluto siempre será positivo; de ahí que podamos concluir que no hay solución.

Geométricamente, podemos ver que nunca\(f(x)=|x+1|+4\) es menor que\(g(x)=3\).

Figura\(\PageIndex{17}\)

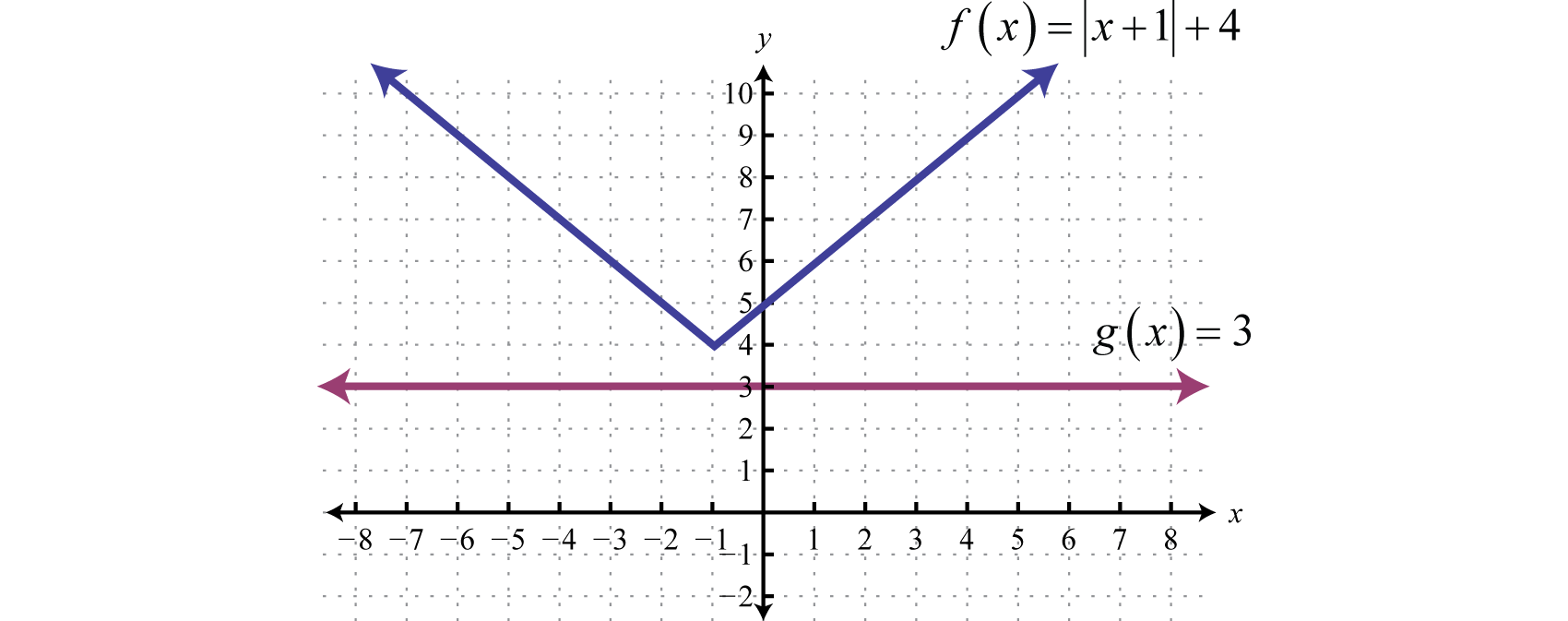
Respuesta:\(Ø\)

En resumen, hay tres casos para ecuaciones de valor absoluto y desigualdades. Las relaciones\(=, <, \leq, > \) y\(≥\) determinar qué teorema aplicar.

Caso 1: Una ecuación de valor absoluto:

\(\begin{array} { c } { \text { If } | X | = p } \\ { \text { then } X = - p \text { or } X = p } \end{array}\)

Figura\(\PageIndex{18}\)

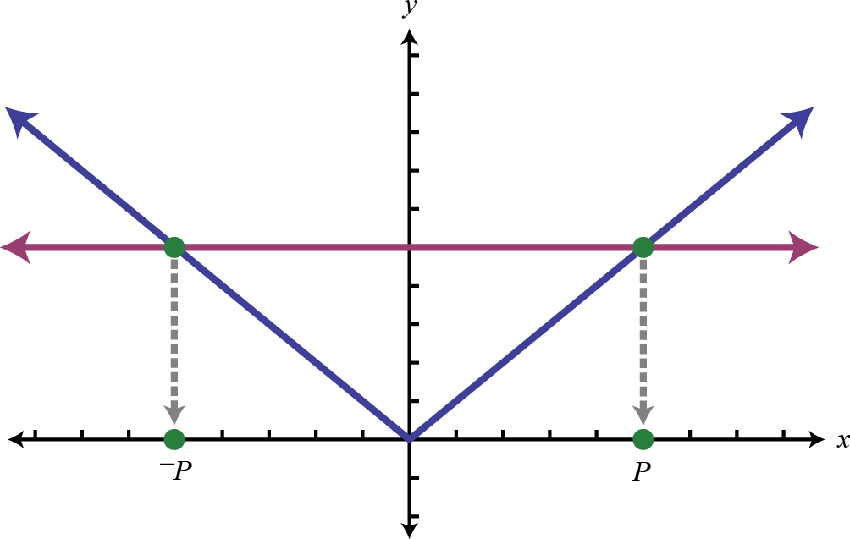
Caso 2: Una desigualdad de valor absoluto que involucra "menor que”.

\(\begin{array} { c } { \text { If } | X | \leq p } \\ { \text { then } - p \leq X \leq p } \end{array}\)

Figura\(\PageIndex{19}\)

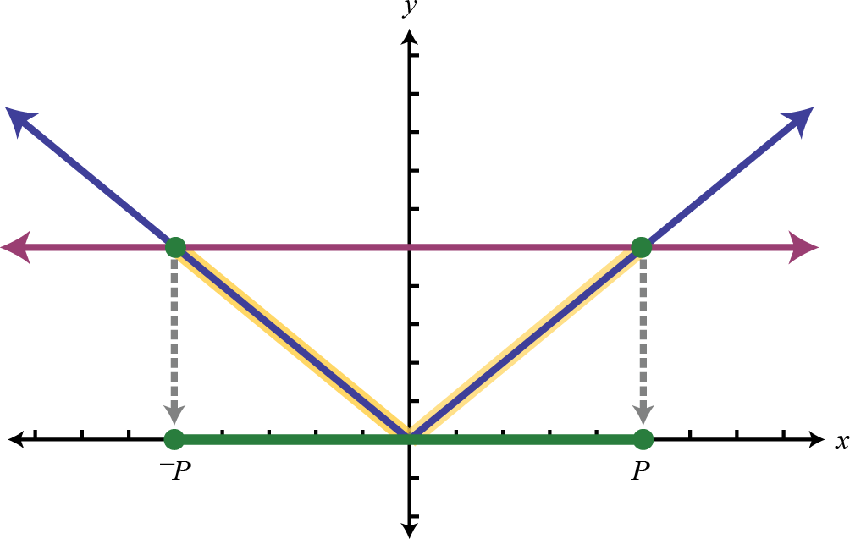
Caso 3: Una desigualdad de valor absoluto que implica "mayor que”.

\(\begin{array} { c } { \text { If } | X | \geq p } \\ { \text { then } X \leq - p \text { or } X \geq p } \end{array}\)

Figura\(\PageIndex{20}\)

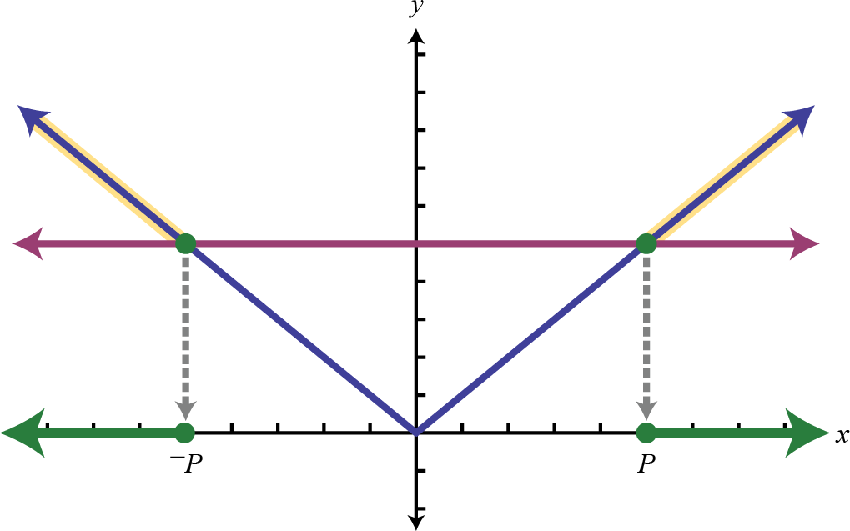
Claves para llevar

• Para resolver una ecuación de valor absoluto, como\(|X| = p\), sustituirla por las dos ecuaciones\(X = −p\)\(X = p\) y luego resolver cada una como de costumbre. Las ecuaciones de valor absoluto pueden tener hasta dos soluciones.
• Resolver una desigualdad de valor absoluto que implique “menos que”, como\(|X| ≤ p\), sustituirla por la desigualdad compuesta\(−p ≤ X ≤ p\) y luego resolverla como de costumbre.
• Resolver una desigualdad de valor absoluto que implique “mayor que”, como\(|X| ≥ p\), sustituirla por la desigualdad compuesta\(X ≤ −p\) o\(X ≥ p\) y luego resolverla como de costumbre.
• Recuerda aislar el valor absoluto antes de aplicar estos teoremas.

Ejercicio\(\PageIndex{5}\)

1. \(|x| = 9\)
2. \(|x| = 1\)
3. \(|x − 7| = 3\)
4. \(|x − 2| = 5\)
5. \(|x + 12| = 0\)
6. \(|x + 8| = 0\)
7. \(|x + 6| = −1\)
8. \(|x − 2| = −5\)
9. \(|2y − 1| = 13\)
10. \(|3y − 5| = 16\)
11. \(|−5t + 1| = 6\)
12. \(|−6t + 2| = 8\)
13. \(\left| \frac { 1 } { 2 } x - \frac { 2 } { 3 } \right| = \frac { 1 } { 6 }\)
14. \(\left| \frac { 2 } { 3 } x + \frac { 1 } { 4 } \right| = \frac { 5 } { 12 }\)
15. \(|0.2x + 1.6| = 3.6\)
16. \(|0.3x − 1.2| = 2.7\)
17. \(| 5 (y − 4) + 5| = 15\)
18. \(| 2 (y − 1) − 3y| = 4\)
19. \(|5x − 7| + 3 = 10\)
20. \(|3x − 8| − 2 = 6\)
21. \(9 + |7x + 1| = 9\)
22. \(4 − |2x − 3| = 4\)
23. \(3 |x − 8| + 4 = 25\)
24. \(2 |x + 6| − 3 = 17\)
25. \(9 + 5 |x − 1| = 4\)
26. \(11 + 6 |x − 4| = 5\)
27. \(8 − 2 |x + 1| = 4\)
28. \(12 − 5 |x − 2| = 2\)
29. \(\frac{1}{2} |x − 5| − \frac{2}{3} = −\frac{1}{6}\)
30. \(\frac { 1 } { 3 } \left| x + \frac { 1 } { 2 } \right| + 1 = \frac { 3 } { 2 }\)
31. \(−2 |7x + 1| − 4 = 2\)
32. \(−3 |5x − 3| + 2 = 5\)
33. \(1.2 |t − 2.8| − 4.8 = 1.2\)
34. \(3.6 | t + 1.8| − 2.6 = 8.2\)
35. \(\frac{1}{2} |2 (3x − 1) − 3| + 1 = 4\)
36. \(\frac{2}{3} |4 (3x + 1) − 1| − 5 = 3\)
37. \(|5x − 7| = |4x − 2|\)
38. \(|8x − 3| = |7x − 12|\)
39. \(|5y + 8| = |2y + 3|\)
40. \(|7y + 2| = |5y − 2|\)
41. \(|5 (x − 2)| = |3x|\)
42. \(|3 (x + 1)| = |7x|\)
43. \(\left| \frac { 2 } { 3 } x + \frac { 1 } { 2 } \right| = \left| \frac { 3 } { 2 } x - \frac { 1 } { 3 } \right|\)
44. \(\left| \frac { 3 } { 5 } x - \frac { 5 } { 2 } \right| = \left| \frac { 1 } { 2 } x + \frac { 2 } { 5 } \right|\)
45. \(|1.5t − 3.5| = |2.5t + 0.5|\)
46. \(|3.2t − 1.4| = |1.8t + 2.8|\)
47. \(|5 − 3 (2x + 1)| = |5x + 2|\)
48. \(|3 − 2 (3x − 2)| = |4x − 1|\)

Contestar

1. \(−9, 9\)

3. \(4, 10\)

5. \(−12\)

7. \(Ø\)

9. \(−6, 7\)

11. \(−1, \frac{7}{5}\)

13. \(1, \frac{5}{3}\)

15. \(−26, 10\)

17. \(0, 6\)

19. \(0, \frac{14}{5}\)

21. \(−\frac{1}{7}\)

23. \(1, 15\)

25. \(Ø\)

27. \(−3, 1\)

29. \(4, 6\)

31. \(Ø\)

33. \(−2.2, 7.8\)

35. \(−\frac{1}{6}, \frac{11}{6}\)

37. \(1, 5\)

39. \(−\frac{5}{3}, −\frac{11}{7}\)

41. \(\frac{5}{4} , 5\)

43. \(−\frac{1}{13} , 1\)

45. \(−4, 0.75\)

47. \(0, 4\)

Ejercicio\(\PageIndex{6}\)

Resuelve y grafica el conjunto de soluciones. Además, dar la solución establecida en notación de intervalos.

1. Resolver para\(x: p |ax + b| − q = 0\)
2. Resolver para\(x: |ax + b| = |p + q|\)

Responder

1. \(x = \frac { - b q \pm q } { a p }\)

Ejercicio\(\PageIndex{7}\)

Resuelve y grafica el conjunto de soluciones. Además, dar la solución establecida en notación de intervalos.

1. \(|x| < 5\)
2. \(|x| ≤ 2\)
3. \(|x + 3| ≤ 1\)
4. \(|x − 7| < 8\)
5. \(|x − 5| < 0\)
6. \(|x + 8| < −7\)
7. \(|2x − 3| ≤ 5\)
8. \(|3x − 9| < 27\)
9. \(|5x − 3| ≤ 0\)
10. \(|10x + 5| < 25\)
11. \(\left| \frac { 1 } { 3 } x - \frac { 2 } { 3 } \right| \leq 1\)
12. \(\left| \frac { 1 } { 12 } x - \frac { 1 } { 2 } \right| \leq \frac { 3 } { 2 }\)
13. \(|x| ≥ 5\)
14. \(|x| > 1\)
15. \(|x + 2| > 8\)
16. \(|x − 7| ≥ 11\)
17. \(|x + 5| ≥ 0\)
18. \(|x − 12| > −4\)
19. \(|2x − 5| ≥ 9\)
20. \(|2x + 3| ≥ 15\)
21. \(|4x − 3| > 9\)
22. \(|3x − 7| ≥ 2\)
23. \(\left| \frac { 1 } { 7 } x - \frac { 3 } { 14 } \right| > \frac { 1 } { 2 }\)
24. \(\left| \frac { 1 } { 2 } x + \frac { 5 } { 4 } \right| > \frac { 3 } { 4 }\)

Responder

1. \(( - 5,5 )\);

Figura\(\PageIndex{21}\)

3. \([ - 4 , - 2 ]\);

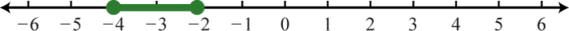
Figura\(\PageIndex{22}\)

5. \(\emptyset\);

Figura\(\PageIndex{23}\)

7. \([ - 1,4 ]\);

Figura\(\PageIndex{24}\)

9. \(\left\{ \frac { 3 } { 5 } \right\}\);

Figura\(\PageIndex{25}\)

11. \([ - 1,5 ]\);

Figura\(\PageIndex{26}\)

13. \(( - \infty , - 5 ] \cup [ 5 , \infty )\);

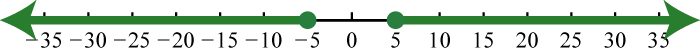
Figura\(\PageIndex{27}\)

15. \(( - \infty , - 10 ) \cup ( 6 , \infty )\);

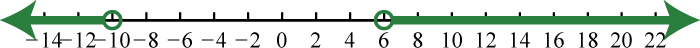
Figura\(\PageIndex{28}\)

17. \(\mathbb { R }\);

Figura\(\PageIndex{29}\)

19. \(( - \infty , - 2 ] \cup [ 7 , \infty )\);

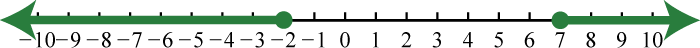
Figura\(\PageIndex{30}\)

21. \(\left( - \infty , - \frac { 3 } { 2 } \right) \cup ( 3 , \infty )\);

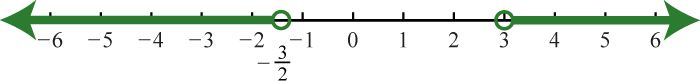
Figura\(\PageIndex{31}\)

23. \(( - \infty , - 2 ) \cup ( 5 , \infty )\);

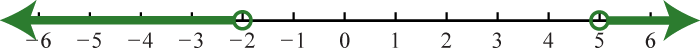
Figura\(\PageIndex{32}\)

Ejercicio\(\PageIndex{8}\)

Resuelve y grafica el conjunto de soluciones.

1. \(|3 (2x − 1)| > 15\)
2. \(|3 (x − 3)| ≤ 21\)
3. \(−5 |x − 4| > −15\)
4. \(−3 |x + 8| ≤ −18\)
5. \(6 − 3 |x − 4| < 3\)
6. \(5 − 2 |x + 4| ≤ −7\)
7. \(6 − |2x + 5| < −5\)
8. \(25 − |3x − 7| ≥ 18\)
9. \(|2x + 25| − 4 ≥ 9\)
10. \(|3 (x − 3)| − 8 < −2\)
11. \(2 |9x + 5| + 8 > 6\)
12. \(3 |4x − 9| + 4 < −1\)
13. \(5 |4 − 3x| − 10 ≤ 0\)
14. \(6 |1 − 4x| − 24 ≥ 0\)
15. \(3 − 2 |x + 7| > −7\)
16. \(9 − 7 |x − 4| < −12\)
17. \(|5 (x − 4) + 5| > 15\)
18. \(|3 (x − 9) + 6| ≤ 3\)
19. \(\left| \frac { 1 } { 3 } ( x + 2 ) - \frac { 7 } { 6 } \right| - \frac { 2 } { 3 } \leq - \frac { 1 } { 6 }\)
20. \(\left| \frac { 1 } { 10 } ( x + 3 ) - \frac { 1 } { 2 } \right| + \frac { 3 } { 20 } > \frac { 1 } { 4 }\)
21. \(12 + 4 |2x − 1| ≤ 12\)
22. \(3 − 6 |3x − 2| ≥ 3\)
23. \(\frac{1}{2} |2x − 1| + 3 < 4\)
24. 2 |\ frac {1} {2} x +\ frac {2} {3} | − 3 ≤ −1\)
25. \(7 − |−4 + 2 (3 − 4x)| > 5\)
26. \(9 − |6 + 3 (2x − 1)| ≥ 8\)
27. \(\frac { 3 } { 2 } - \left| 2 - \frac { 1 } { 3 } x \right| < \frac { 1 } { 2 }\)
28. \(\frac { 5 } { 4 } - \left| \frac { 1 } { 2 } - \frac { 1 } { 4 } x \right| < \frac { 3 } { 8 }\)

Responder

1. \(( - \infty , - 2 ) \cup ( 3 , \infty )\);

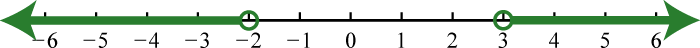
Figura\(\PageIndex{33}\)

3. \(( 1,7 )\);

Figura\(\PageIndex{34}\)

5. \(( - \infty , 3 ) \cup ( 5 , \infty )\);

Figura\(\PageIndex{35}\)

7. \(( - \infty , - 8 ) \cup ( 3 , \infty )\);

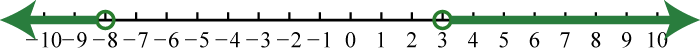
Figura\(\PageIndex{36}\)

9. \(( - \infty , - 19 ] \cup [ - 6 , \infty )\);

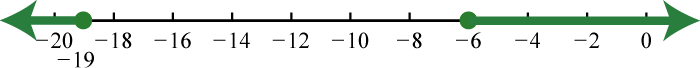
Figura\(\PageIndex{37}\)

11. \(\mathbb { R }\);

Figura\(\PageIndex{38}\)

13. \(\left[ \frac { 2 } { 3 } , 2 \right]\);

Figura\(\PageIndex{39}\)

15. \(( - 12 , - 2 )\);

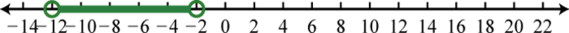
Figura\(\PageIndex{40}\)

17. \(( - \infty , 0 ) \cup ( 6 , \infty )\);

Figura\(\PageIndex{41}\)

19. \([ 0,3 ]\);

Figura\(\PageIndex{42}\)

21. \(\frac { 1 } { 2 }\);

Figura\(\PageIndex{43}\)

23. \(\left( - \frac { 1 } { 2 } , \frac { 3 } { 2 } \right)\);

Figura\(\PageIndex{44}\)

25. \(\left( 0 , \frac { 1 } { 2 } \right)\);

Figura\(\PageIndex{45}\)

27. \(( - \infty , 3 ) \cup ( 9 , \infty )\);

Figura\(\PageIndex{46}\)

Ejercicio\(\PageIndex{9}\)

Supongamos que todas las variables en el denominador son distintas de cero.

1. Resuelve para\(x\) donde\(a, p > 0: p |ax + b| − q ≤ 0\)
2. Resuelve para\(x\) donde\(a, p > 0: p |ax + b| − q ≥ 0\)

Responder

1. \(\frac { - q - b p } { a p } \leq x \leq \frac { q - b p } { a p }\)

Ejercicio\(\PageIndex{10}\)

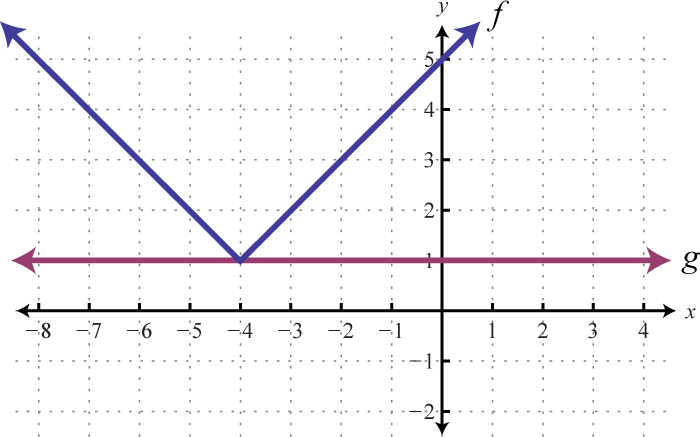
Dada la gráfica de\(f\) y\(g\), determinar los\(x\) -valores donde:

a)\(f ( x ) = g ( x )\)

b)\(f ( x ) > g ( x )\)

c)\(f ( x ) < g ( x )\)

1.

Figura\(\PageIndex{47}\)

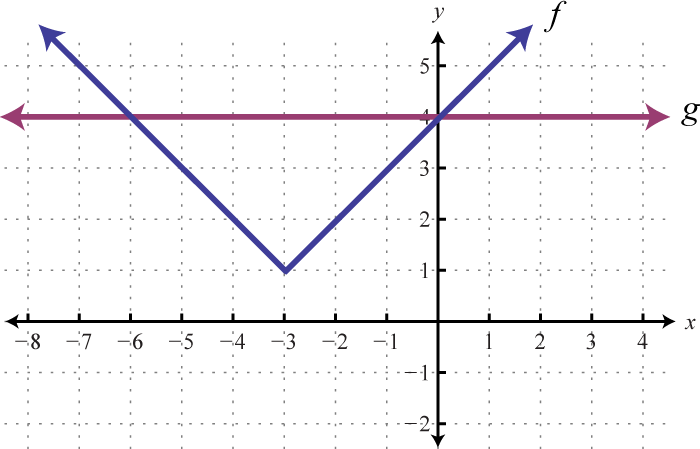
2.

Figura\(\PageIndex{48}\)

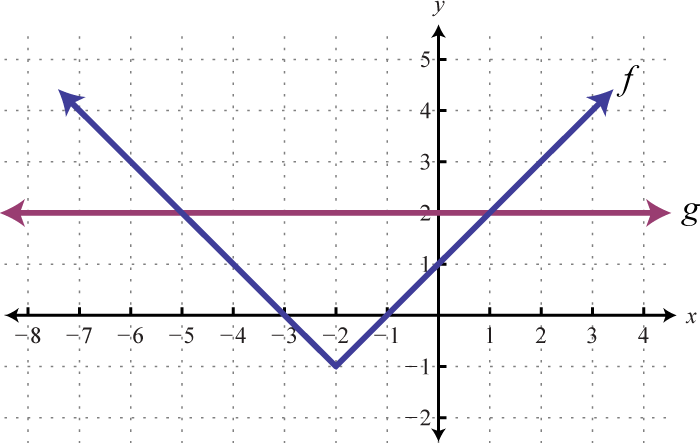
3.

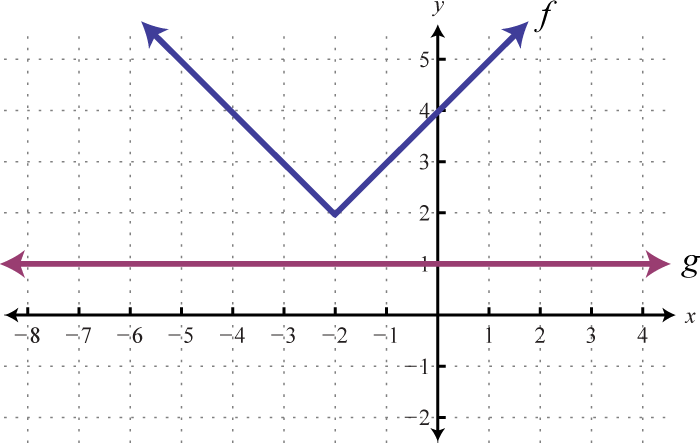
Figura\(\PageIndex{49}\)

4.

Figura\(\PageIndex{50}\)

Responder

1. a)\(−6, 0\), b)\((−∞, −6) ∪ (0, ∞)\), c\((−6, 0)\)

3. a)\(Ø\), b)\(ℝ\), c\(Ø\)

Ejercicio\(\PageIndex{11}\)

1. Hacer tres tarjetas de notas, una para cada uno de los tres casos descritos en esta sección. Por un lado escribe el teorema, y por el otro escribe una solución completa a un ejemplo representativo. Comparta su estrategia para identificar y resolver ecuaciones de valores absolutos y desigualdades en el tablero de discusión.
2. Haz tus propios ejemplos de ecuaciones de valor absoluto y desigualdades que no tengan solución, al menos una para cada caso descrito en esta sección. Ilustra tus ejemplos con una gráfica.

Responder

1. La respuesta puede variar

Notas al pie

⁶³ La distancia desde la gráfica de un número\(a\) a cero en una recta numérica, denotada\(|a|\).

⁶⁴ El número o expresión dentro del valor absoluto.