8.E: Secciones Cónicas (Ejercicios)
- Page ID
- 109916
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ejercicio\(\PageIndex{1}\)
Calcular la distancia y el punto medio entre los dos puntos dados.
- \((0,2)\)y\((-4,-1)\)
- \((6,0)\)y\((-2,-6)\)
- \((-2,4)\)y\((-6,-8)\)
- \(\left(\frac{1}{2},-1\right)\)y\(\left(\frac{5}{2},-\frac{1}{2}\right)\)
- \((0,-3 \sqrt{2})\)y\((\sqrt{5},-4 \sqrt{2})\)
- \((-5 \sqrt{3}, \sqrt{6})\)y\((-3 \sqrt{3}, \sqrt{6})\)
- Contestar
-
1. Distancia:\(5\) unidades; punto medio:\(\left(-2, \frac{1}{2}\right)\)
3. Distancia:\(4\sqrt{10}\) unidades; punto medio:\((-4,-2)\)
5. Distancia:\(\sqrt{7}\) unidades; punto medio:\(\left(\frac{\sqrt{5}}{2},-\frac{7 \sqrt{2}}{2}\right)\)
Ejercicio\(\PageIndex{2}\)
Determinar el área de un círculo cuyo diámetro está definido por los dos puntos dados.
- \((-3,3)\)y\((3,-3)\)
- \((-2,-9)\)y\((-10,-15)\)
- \(\left(\frac{2}{3},-\frac{1}{2}\right)\)y\(\left(-\frac{1}{3}, \frac{3}{2}\right)\)
- \((2 \sqrt{5},-2 \sqrt{2})\)y\((0,-4 \sqrt{2})\)
- Contestar
-
1. \(18\pi\)unidades cuadradas
3. \(\frac{5 \pi}{4}\)unidades cuadradas
Ejercicio\(\PageIndex{3}\)
Reescribe en forma estándar y da el vértice.
- \(y=x^{2}-10 x+33\)
- \(y=2 x^{2}-4 x-1\)
- \(y=x^{2}-3 x-1\)
- \(y=-x^{2}-x-2\)
- \(x=y^{2}+10 y+10\)
- \(x=3 y^{2}+12 y+7\)
- \(x=-y^{2}+8 y-3\)
- \(x=5 y^{2}-5 y+2\)
- Contestar
-
1. \(y=(x-5)^{2}+8 ;\)vértice:\((5,8)\)
3. \(y=\left(x-\frac{3}{2}\right)^{2}-\frac{13}{4} ;\)vértice:\(\left(\frac{3}{2},-\frac{13}{4}\right)\)
5. \(x=(y+5)^{2}-15 ;\)vértice:\((-15,-5)\)
7. \(x=-(y-4)^{2}+13 ;\)vértice:\((13,4)\)
Ejercicio\(\PageIndex{4}\)
Reescribir en forma estándar y gráfica. Asegúrate de encontrar el vértice y todas las intercepciones.
- \(y=x^{2}-20 x+75\)
- \(y=-x^{2}-10 x+75\)
- \(y=-2 x^{2}-12 x-24\)
- \(y=4 x^{2}+4 x+6\)
- \(x=y^{2}-10 y+16\)
- \(x=-y^{2}+4 y+12\)
- \(x=-4 y^{2}+12 y\)
- \(x=9 y^{2}+18 y+12\)
- \(x=-4 y^{2}+4 y+2\)
- \(x=-y^{2}-5 y+2\)
- Contestar
-
1. \(y=(x-10)^{2}-25\);
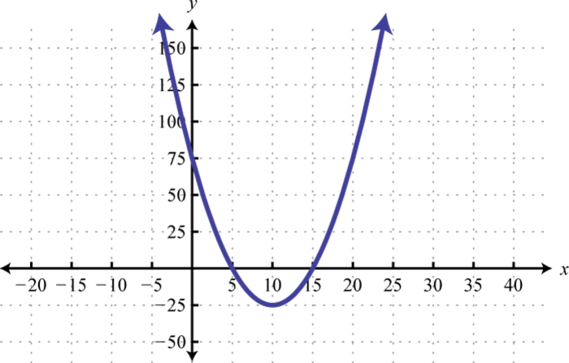
Figura 8.E.1 3. \(y=-2(x+3)^{2}-6\);
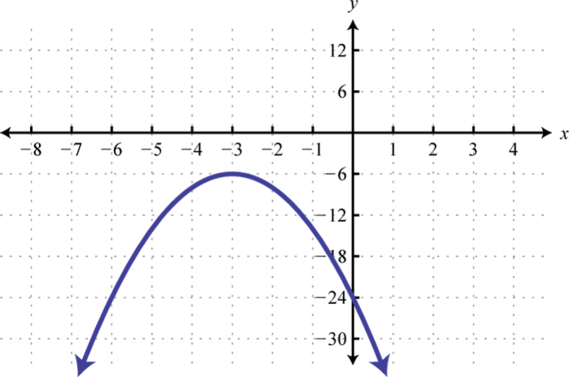
Figura 8.E.2 5. \(x=(y-5)^{2}-9\);

Figura 8.E.3 7. \(x=-4\left(y-\frac{3}{2}\right)^{2}+9\);
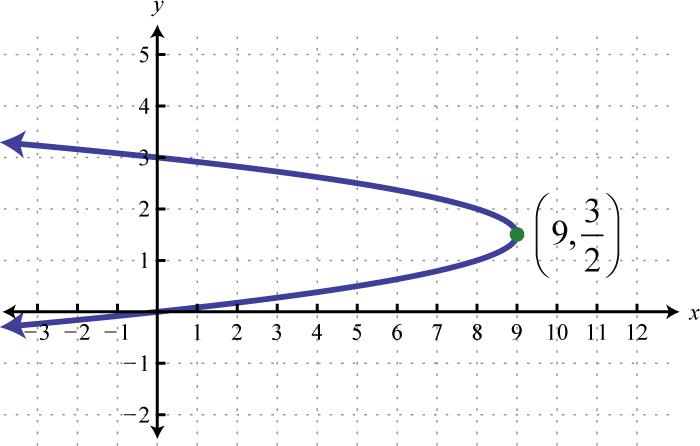
Figura 8.E.4 9. \(x=-4\left(y-\frac{1}{2}\right)^{2}+3\);
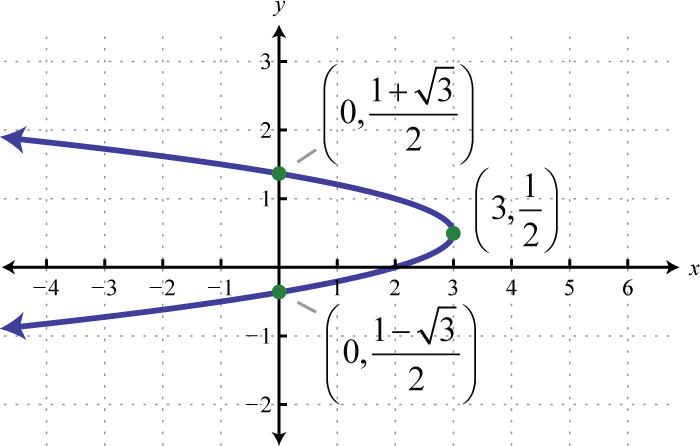
Figura 8.E.5
Ejercicio\(\PageIndex{5}\)
Determinar el centro y el radio dada la ecuación de un círculo en forma estándar.
- \((x-6)^{2}+y^{2}=9\)
- \((x+8)^{2}+(y-10)^{2}=1\)
- \(x^{2}+y^{2}=5\)
- \(\left(x-\frac{3}{8}\right)^{2}+\left(y+\frac{5}{2}\right)^{2}=\frac{1}{2}\)
- Contestar
-
1. Centro:\((6,0) ;\) radio:\(r=3\)
3. Centro:\((0,0) ;\) radio:\(r=\sqrt{5}\)
Ejercicio\(\PageIndex{6}\)
Determine la forma estándar para la ecuación del círculo:
- Centro\((-7,2)\) con radio\(r=10\)
- Centro\(\left(\frac{1}{3},-1\right)\) con radio\(r=\frac{2}{3}\)
- Centro\((0,-5)\) con radio\(r=2 \sqrt{7}\)
- Centro\((1,0)\) con radio\(r=\frac{5 \sqrt{3}}{2}\)
- Círculo cuyo diámetro está definido por\((-4,10)\) y\((-2,8)\)
- Círculo cuyo diámetro está definido por\((3,-6)\) y\((0,-4)\)
- Contestar
-
1. \((x+7)^{2}+(y-2)^{2}=100\)
3. \(x^{2}+(y+5)^{2}=28\)
5. \((x+3)^{2}+(y-9)^{2}=2\)
Ejercicio\(\PageIndex{7}\)
Encuentra los\(x\) - y\(y\) -interceptos.
- \((x-3)^{2}+(y+5)^{2}=16\)
- \((x+5)^{2}+(y-1)^{2}=4\)
- \(x^{2}+(y-2)^{2}=20\)
- \((x-3)^{2}+(y+3)^{2}=8\)
- \(x^{2}+y^{2}-12 y+27=0\)
- \(x^{2}+y^{2}-4 x+2 y+1=0\)
- Contestar
-
1. \(x\)-intercepta: ninguno;\(y\) -intercepta:\((0,-5 \pm \sqrt{7})\)
3. \(x\)-intercepta:\((\pm 4,0)\);\(y\) -intercepta:\((0,2 \pm 2 \sqrt{5})\)
5. \(x\)-intercepta: ninguno;\(y\) -intercepta:\((0,3),(0,9)\)
Ejercicio\(\PageIndex{8}\)
Gráfica.
- \((x+8)^{2}+(y-6)^{2}=4\)
- \((x-20)^{2}+\left(y+\frac{15}{2}\right)^{2}=\frac{225}{4}\)
- \(x^{2}+y^{2}=24\)
- \((x-1)^{2}+y^{2}=\frac{1}{4}\)
- \(x^{2}+(y-7)^{2}=27\)
- \((x+1)^{2}+(y-1)^{2}=2\)
- Contestar
-
1.

Figura 8.E.6 3.
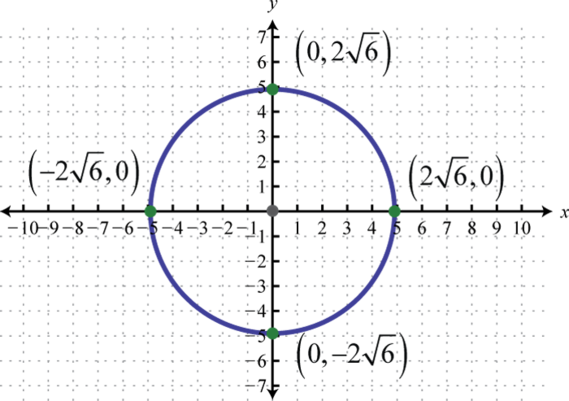
Figura 8.E.7 5.
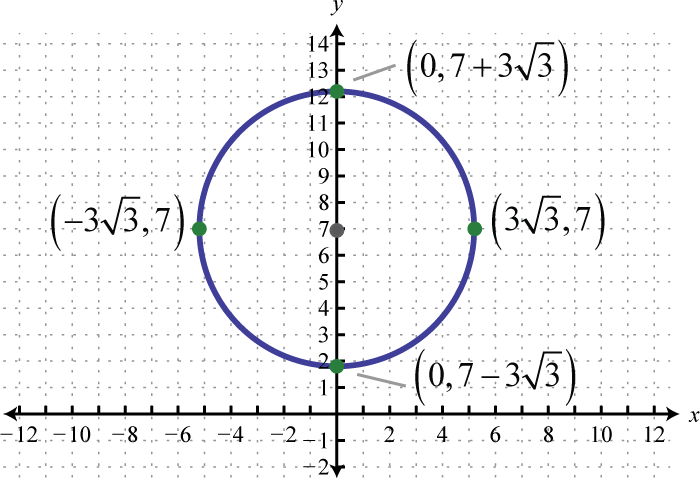
Figura 8.E.8
Ejercicio\(\PageIndex{9}\)
Reescribir en forma estándar y gráfica.
- \(x^{2}+y^{2}-6 x+4 y-3=0\)
- \(x^{2}+y^{2}+8 x-10 y+16=0\)
- \(2 x^{2}+2 y^{2}-2 x-6 y-3=0\)
- \(4 x^{2}+4 y^{2}+8 y+1=0\)
- \(x^{2}+y^{2}-5 x+y-\frac{1}{2}=0\)
- \(x^{2}+y^{2}+12 x-8 y=0\)
- Contestar
-
1. \((x-3)^{2}+(y+2)^{2}=16\);

Figura 8.E.9 3. \(\left(x-\frac{1}{2}\right)^{2}+\left(y-\frac{3}{2}\right)^{2}=4\);
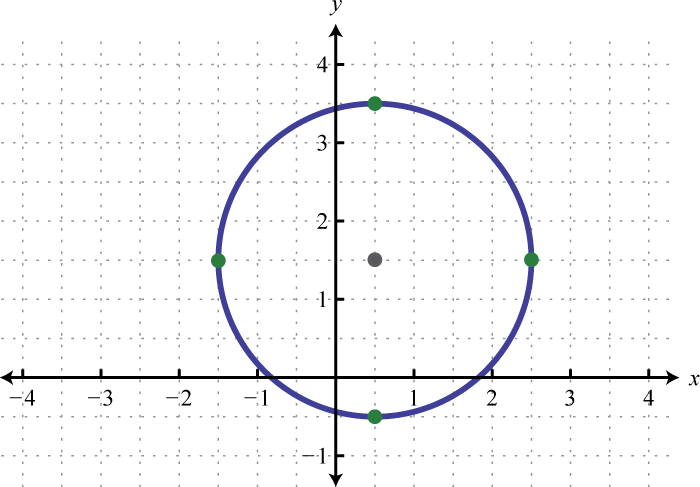
Figura 8.E.10 5. \(\left(x-\frac{5}{2}\right)^{2}+\left(y+\frac{1}{2}\right)^{2}=7\);

Figura 8.E.11
Ejercicio\(\PageIndex{10}\)
Dada la ecuación de una elipse en forma estándar, determine su centro, orientación, radio mayor y radio menor.
- \(\frac{(x+12)^{2}}{16}+\frac{(y-10)^{2}}{4}=1\)
- \(\frac{(x+3)^{2}}{3}+\frac{y^{2}}{25}=1\)
- \(x^{2}+\frac{(y-5)^{2}}{12}=1\)
- \(\frac{(x-8)^{2}}{5}+\frac{(y+8)}{18}=1\)
- Contestar
-
1. Centro:\((−12, 10)\); orientación: horizontal; radio mayor:\(4\) unidades; radio menor:\(2\) unidades
3. Centro:\((0, 5)\); orientación: vertical; radio mayor:\(2\sqrt{3}\) unidades; radio menor:\(1\) unidad
Ejercicio\(\PageIndex{11}\)
Determinar la forma estándar para la ecuación de la elipse dada la siguiente información.
- Centro\((0,-4)\) con\(a=3\) y\(b=4\)
- Centro\((3,8)\) con\(a=1\) y\(b=\sqrt{7}\)
- Centro\((0,0)\) con\(a=5\) y\(b=\sqrt{2}\)
- Centro\((-10,-30)\) con\(a=10\) y\(b=1\)
- Contestar
-
1. \(\frac{x^{2}}{9}+\frac{(y+4)^{2}}{16}=1\)
3. \(\frac{x^{2}}{25}+\frac{y^{2}}{2}=1\)
Ejercicio\(\PageIndex{12}\)
Encuentra los\(x\) - y\(y\) -interceptos.
- \(\frac{(x+2)^{2}}{4}+\frac{y^{2}}{9}=1\)
- \(\frac{(x-1)^{2}}{2}+\frac{(y+1)^{2}}{3}=1\)
- \(5 x^{2}+2 y^{2}=20\)
- \(5(x-3)^{2}+6 y^{2}=120\)
- Contestar
-
1. \(x\)-intercepta:\((-4,0),(0,0) ; y\) -intercepta:\((0,0)\)
3. \(x\)-intercepta:\((\pm 2,0) ; y\) -intercepta:\((0, \pm \sqrt{10})\)
Ejercicio\(\PageIndex{13}\)
Gráfica.
- \(\frac{(x-10)^{2}}{25}+\frac{(y+5)^{2}}{4}=1\)
- \(\frac{(x+6)^{2}}{9}+\frac{(y-8)^{2}}{36}=1\)
- \(\frac{\left(x-\frac{3}{2}\right)^{2}}{4}+\left(y-\frac{7}{2}\right)^{2}=1\)
- \(\left(x-\frac{2}{3}\right)^{2}+\frac{y^{2}}{4}=1\)
- \(\frac{x^{2}}{2}+\frac{y^{2}}{5}=1\)
- \(\frac{(x+2)^{2}}{8}+\frac{(y-3)^{2}}{12}=1\)
- Contestar
-
1.
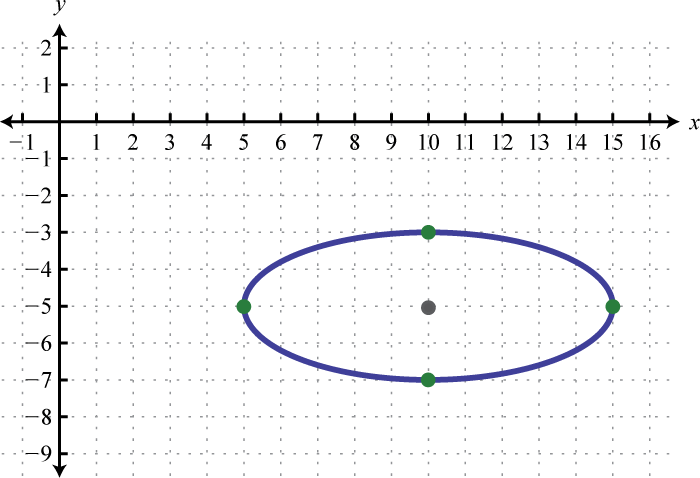
Figura 8.E.12 3.
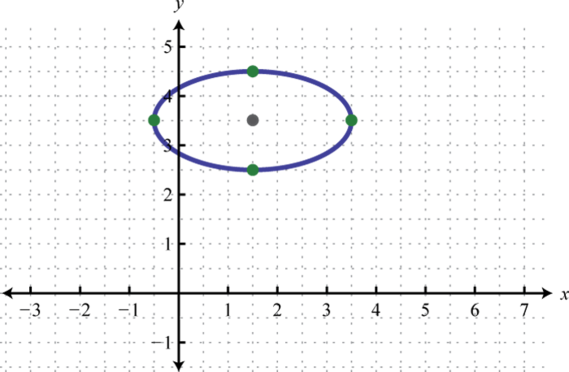
Figura 8.E.13 5.
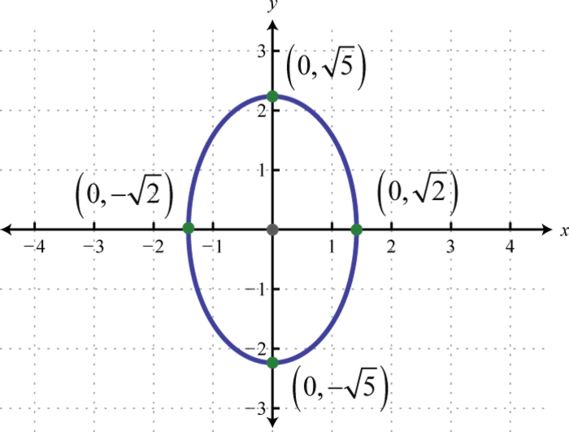
Figura 8.E.14
Ejercicio\(\PageIndex{14}\)
Reescribir en forma estándar y gráfica.
- \(4 x^{2}+9 y^{2}-8 x+90 y+193=0\)
- \(9 x^{2}+4 y^{2}+108 x-80 y+580=0\)
- \(x^{2}+9 y^{2}+6 x+108 y+324=0\)
- \(25 x^{2}+y^{2}-350 x-8 y+1,216=0\)
- \(8 x^{2}+12 y^{2}-16 x-36 y-13=0\)
- \(10 x^{2}+2 y^{2}-50 x+14 y+7=0\)
- Contestar
-
1. \(\frac{(x-1)^{2}}{9}+\frac{(y+5)^{2}}{4}=1\);
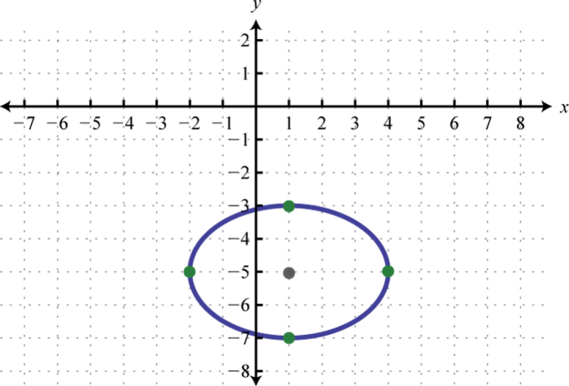
Figura 8.E.15 3. \(\frac{(x+3)^{2}}{9}+(y+6)^{2}=1\);

Figura 8.E.16 5. \(\frac{(x-1)^{2}}{6}+\frac{\left(y-\frac{3}{2}\right)^{2}}{4}=1\);

Figura 8.E.17
Ejercicio\(\PageIndex{15}\)
Dada la ecuación de una hipérbola en forma estándar, determinar su centro, en qué dirección se abre la gráfica, y los vértices.
- \(\frac{(x-10)^{2}}{4}-\frac{(y+5)^{2}}{16}=1\)
- \(\frac{(x+7)^{2}}{2}-\frac{(y-8)^{2}}{8}=1\)
- \(\frac{(y-20)^{2}}{3}-(x-15)^{2}=1\)
- \(3 y^{2}-12(x-1)^{2}=36\)
- Contestar
-
1. Centro:\((10,-5)\); abre izquierda y derecha; vértices:\((8,-5),(12,-5)\)
3. Centro:\((15,20)\); se abre hacia arriba y hacia abajo; vértices:\((15,20-\sqrt{3}),(15,20+\sqrt{3})\)
Ejercicio\(\PageIndex{16}\)
Determinar la forma estándar para la ecuación de la hipérbola.
- El centro\((-25,10), a=3, b=\sqrt{5},\) se abre hacia arriba y hacia abajo.
- El centro\((9,-12), a=5 \sqrt{3}, b=7,\) se abre a izquierda y derecha.
- El centro\((-4,0), a=1, b=6,\) se abre a izquierda y derecha.
- El centro\((-2,-3), a=10 \sqrt{2}, b=2 \sqrt{3},\) se abre hacia arriba y hacia abajo.
- Contestar
-
1. \(\frac{(y-10)^{2}}{5}-\frac{(x+25)^{2}}{9}=1\)
3. \((x+4)^{2}-\frac{y^{2}}{36}=1\)
Ejercicio\(\PageIndex{17}\)
Encuentra los\(x\) - y\(y\) -interceptos.
- \(\frac{(x-1)^{2}}{4}-\frac{(y+3)^{2}}{9}=1\)
- \(\frac{(x+4)^{2}}{8}-\frac{(y-2)^{2}}{12}=1\)
- \(4(y-2)^{2}-x^{2}=16\)
- \(6(y+1)^{2}-3(x-1)^{2}=18\)
- Contestar
-
1. \(x\)-intercepta:\((1 \pm 2 \sqrt{2}, 0) ; y\) -intercepta: ninguna
3. \(x\)-intercepta:\((0,0) ; y\) -intercepta:\((0,0),(0,4)\)
Ejercicio\(\PageIndex{18}\)
Gráfica.
- \(\frac{(x-10)^{2}}{25}-\frac{(y+5)^{2}}{100}=1\)
- \(\frac{(x-4)^{2}}{4}-\frac{(y-8)^{2}}{16}=1\)
- \(\frac{(y-3)^{2}}{9}-\frac{(x-6)^{2}}{81}=1\)
- \(\frac{(y+1)^{2}}{4}-\frac{(x+1)^{2}}{25}=1\)
- \(\frac{y^{2}}{27}-\frac{(x-3)^{2}}{9}=1\)
- \(\frac{x^{2}}{2}-\frac{y^{2}}{3}=1\)
- Contestar
-
1.
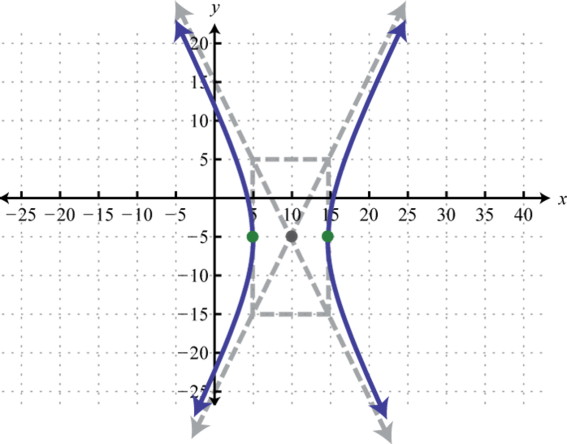
Figura 8.E.18 3.
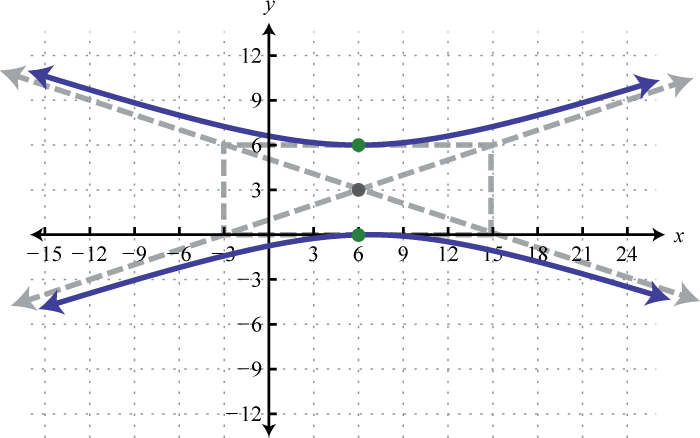
Figura 8.E.19 5.
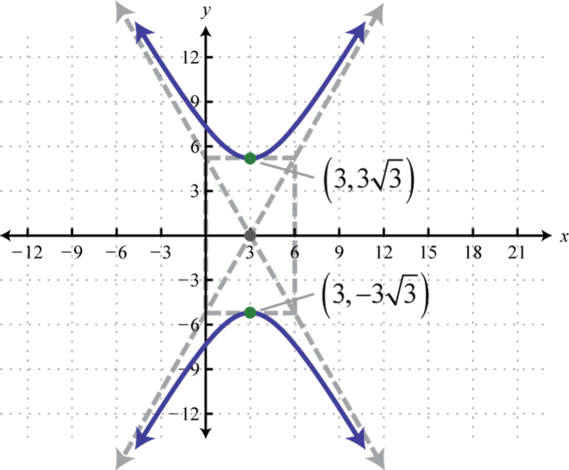
Figura 8.E.20
Ejercicio\(\PageIndex{19}\)
Reescribir en forma estándar y gráfica.
- \(4 x^{2}-9 y^{2}-8 x-90 y-257=0\)
- \(9 x^{2}-y^{2}-108 x+16 y+224=0\)
- \(25 y^{2}-2 x^{2}-100 y+50=0\)
- \(3 y^{2}-x^{2}-2 x-10=0\)
- \(8 y^{2}-12 x^{2}+24 y-12 x-33=0\)
- \(4 y^{2}-4 x^{2}-16 y-28 x-37=0\)
- Contestar
-
1. \(\frac{(x-1)^{2}}{9}-\frac{(y+5)^{2}}{4}=1\);
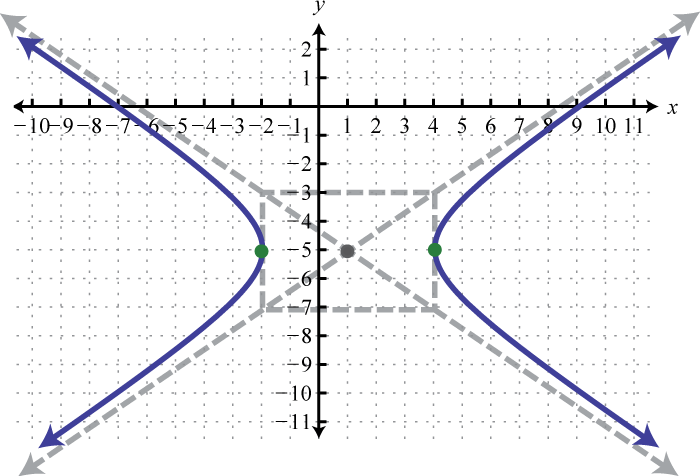
Figura 8.E.21 3. \(\frac{(y-2)^{2}}{2}-\frac{x^{2}}{25}=1\);
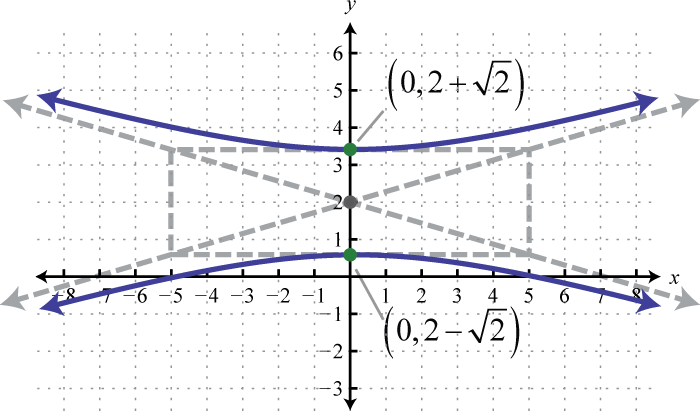
Figura 8.E.22 5. \(\frac{\left(y+\frac{3}{2}\right)^{2}}{6}-\frac{\left(x+\frac{1}{2}\right)^{2}}{4}=1\)

Figura 8.E.23
Ejercicio\(\PageIndex{20}\)
Identificar las secciones cónicas y reescribir en forma estándar.
- \(x^{2}+y^{2}-2 x-8 y+16=0\)
- \(x^{2}+2 y^{2}+4 x-24 y+74=0\)
- \(x^{2}-y^{2}-6 x-4 y+3=0\)
- \(x^{2}+y-10 x+22=0\)
- \(x^{2}+12 y^{2}-12 x+24=0\)
- \(x^{2}+y^{2}+10 y+22=0\)
- \(4 y^{2}-20 x^{2}+16 y+20 x-9=0\)
- \(16 x-16 y^{2}+24 y-25=0\)
- \(9 x^{2}-9 y^{2}-6 x-18 y-17=0\)
- \(4 x^{2}+4 y^{2}+4 x-8 y+1=0\)
- Contestar
-
1. Círculo;\((x-1)^{2}+(y-4)^{2}=1\)
3. hipérbola;\(\frac{(x-3)^{2}}{2}-\frac{(y+2)^{2}}{2}=1\)
5. Elipse;\(\frac{(x-6)^{2}}{12}+y^{2}=1\)
7. hipérbola;\(\frac{(y+2)^{2}}{5}-\left(x-\frac{1}{2}\right)^{2}=1\)
9. hipérbola;\(\left(x-\frac{1}{3}\right)^{2}-(y+1)^{2}=1\)
Ejercicio\(\PageIndex{21}\)
Dada la gráfica, escribir la ecuación en forma general.
1.
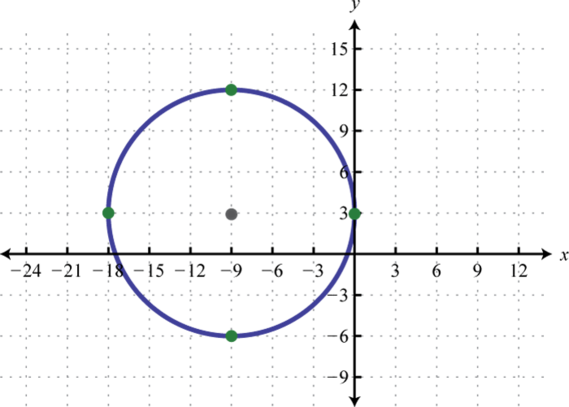
2.
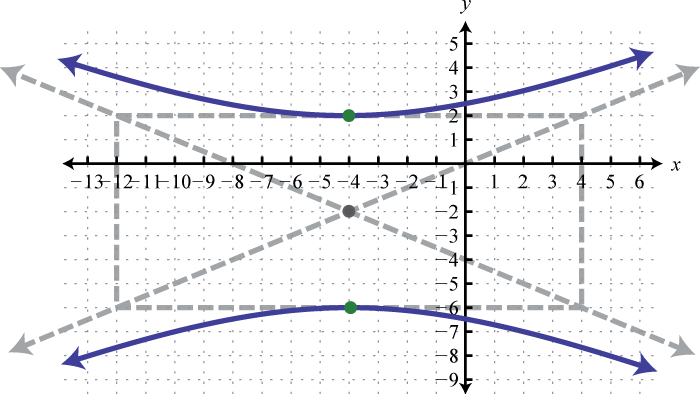
3.

4.

5.
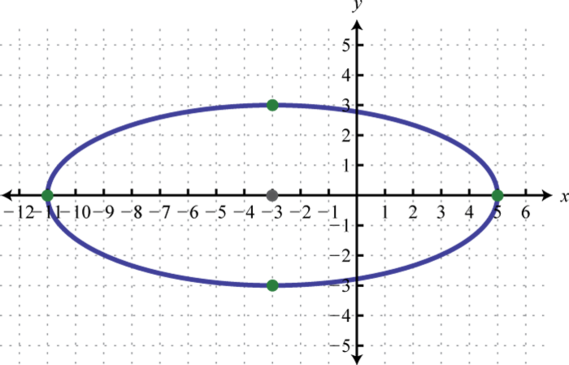
6.

- Contestar
-
1. \(x^{2}+y^{2}+18 x-6 y+9=0\)
3. \(9 x^{2}-y^{2}+72 x-12 y+72=0\)
5. \(9 x^{2}+64 y^{2}+54 x-495=0\)
Ejercicio\(\PageIndex{22}\)
Resolver.
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=8} \\ {x-y=4}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {x+2 y=1}\end{array}\right.\)
- \(\left\{\begin{array}{c}{x^{2}+3 y^{2}=4} \\ {2 x-y=1}\end{array}\right.\)
- \(\left\{\begin{array}{c}{2 x^{2}+y^{2}=5} \\ {x+y=3}\end{array}\right.\)
- \(\left\{\begin{array}{c}{3 x^{2}-2 y^{2}=1} \\ {x-y=2}\end{array}\right.\)
- \(\left\{\begin{array}{c}{x^{2}-3 y^{2}=10} \\ {x-2 y=1}\end{array}\right.\)
- \(\left\{\begin{array}{c}{2 x^{2}+y^{2}=11} \\ {4 x+y^{2}=5}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=1} \\ {2 x^{2}+4 y=5}\end{array}\right.\)
- \(\left\{\begin{array}{c}{5 x^{2}-y^{2}=10} \\ {x^{2}+y=2}\end{array}\right.\)
- \(\left\{\begin{array}{l}{2 x^{2}+y^{2}=1} \\ {2 x-4 y^{2}=-3}\end{array}\right.\)
- \(\left\{\begin{array}{c}{x^{2}+4 y^{2}=10} \\ {x y=2}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y+x^{2}=0} \\ {x y-8=0}\end{array}\right.\)
- \(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=10} \\ {\frac{1}{x}-\frac{1}{y}=6}\end{array}\right.\)
- \(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=1} \\ {y-x=2}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x-2 y^{2}=3} \\ {y=\sqrt{x-4}}\end{array}\right.\)
- \(\left\{\begin{array}{c}{(x-1)^{2}+y^{2}=1} \\ {y-\sqrt{x}=0}\end{array}\right.\)
- Contestar
-
1. \((2,-2)\)
3. \(\left(-\frac{1}{13},-\frac{15}{13}\right),(1,1)\)
5. \((-9,-11),(1,-1)\)
7. \((-1,-3),(-1,3)\)
9. \((-\sqrt{2}, 0),(\sqrt{2}, 0),(-\sqrt{7},-5),(\sqrt{7},-5)\)
11. \((\sqrt{2}, \sqrt{2}) \cdot(-\sqrt{2},-\sqrt{2}) \cdot\left(2 \sqrt{2}, \frac{\sqrt{2}}{2}\right) \cdot\left(-2 \sqrt{2},-\frac{\sqrt{2}}{2}\right)\)
13. \(\left(\frac{1}{8}, \frac{1}{2}\right)\)
15. \((5,1)\)
Examen de muestra
Ejercicio\(\PageIndex{23}\)
- Teniendo en cuenta dos puntos\((-4,-6)\) y\((2,-8)\):
- Calcula la distancia entre ellos.
- Encuentra el punto medio entre ellos.
- Determinar el área de un círculo cuyo diámetro está definido por los puntos\((4, −3)\) y\((−1, 2)\).
- Contestar
-
1. (1)\(2\sqrt{10}\) unidades; (2)\((-1,-7)\)
Ejercicio\(\PageIndex{24}\)
Reescribir en forma estándar y gráfica. Encuentra el vértice y todas las intercepciones si las hay.
- \(y=-x^{2}+6 x-5\)
- \(x=2 y^{2}+4 y-6\)
- \(x=-3 y^{2}+3 y+1\)
- Encuentra la ecuación de un círculo en forma estándar con\(2 \sqrt{5}\) unidades de centro\((−6, 3)\) y radio.
- Contestar
-
1. \(y=-(x-3)^{2}+4\);
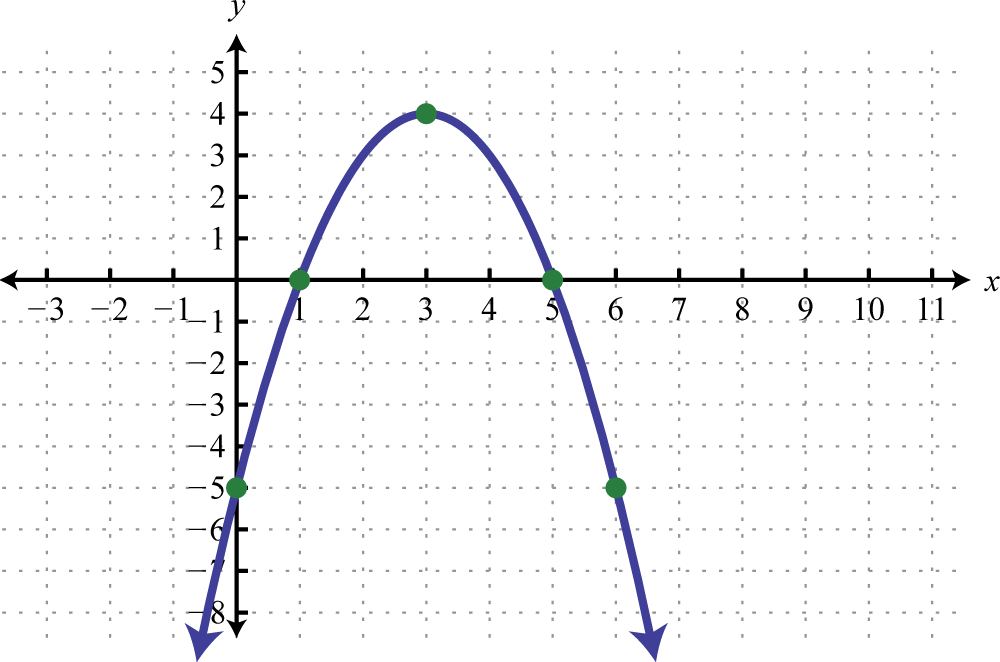
Figura 8.E.30 3. \(x=-3\left(y-\frac{1}{2}\right)^{2}+\frac{7}{4}\);
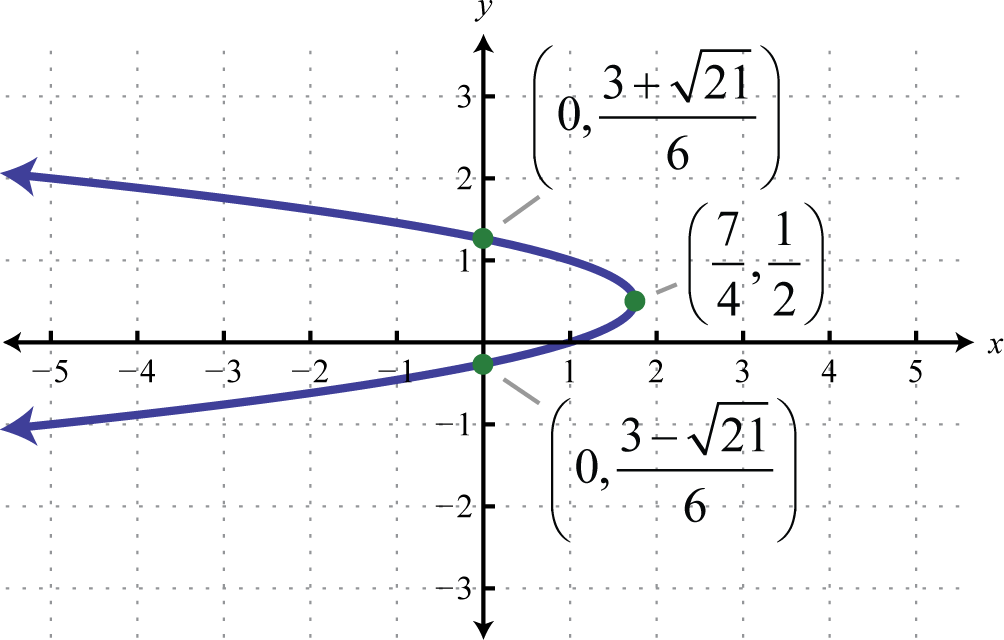
Figura 8.E.31
Ejercicio\(\PageIndex{25}\)
Esbozar la gráfica de la sección cónica dada su ecuación en forma estándar.
- \((x-4)^{2}+(y+1)^{2}=45\)
- \(\frac{(x+3)^{2}}{4}+\frac{y^{2}}{9}=1\)
- \(\frac{y^{2}}{3}-\frac{x^{2}}{9}=1\)
- \(\frac{x^{2}}{16}-(y-2)^{2}=1\)
- Contestar
-
1.

Figura 8.E.32 3.
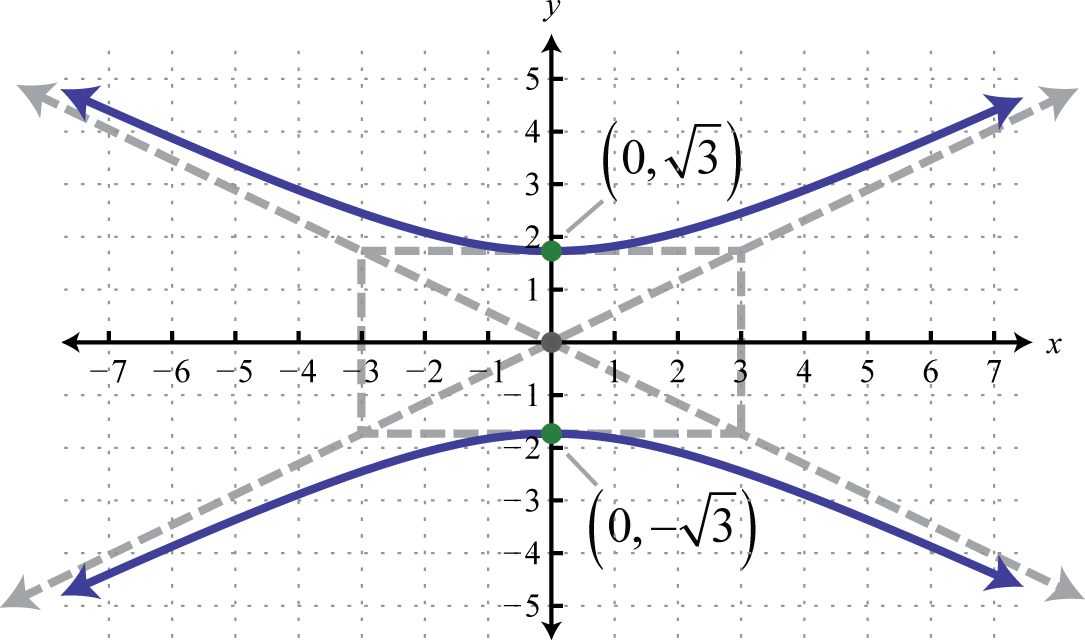
Figura 8.E.33
Ejercicio\(\PageIndex{26}\)
Reescribir en forma estándar y gráfica.
- \(9 x^{2}+4 y^{2}-144 x+16 y+556=0\)
- \(x-y^{2}+6 y+7=0\)
- \(x^{2}+y^{2}+20 x-20 y+100=0\)
- \(4 y^{2}-x^{2}+40 y-30 x-225=0\)
- Contestar
-
1. \(\frac{(x-8)^{2}}{4}+\frac{(y+2)^{2}}{9}=1\);
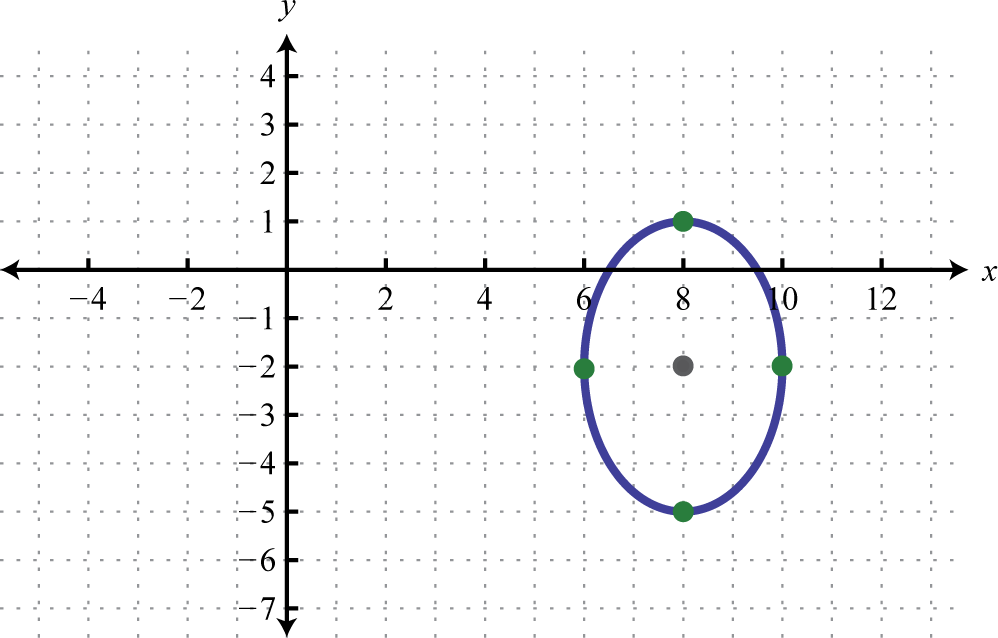
Figura 8.E.34 3. \((x+10)^{2}+(y-10)^{2}=100\);
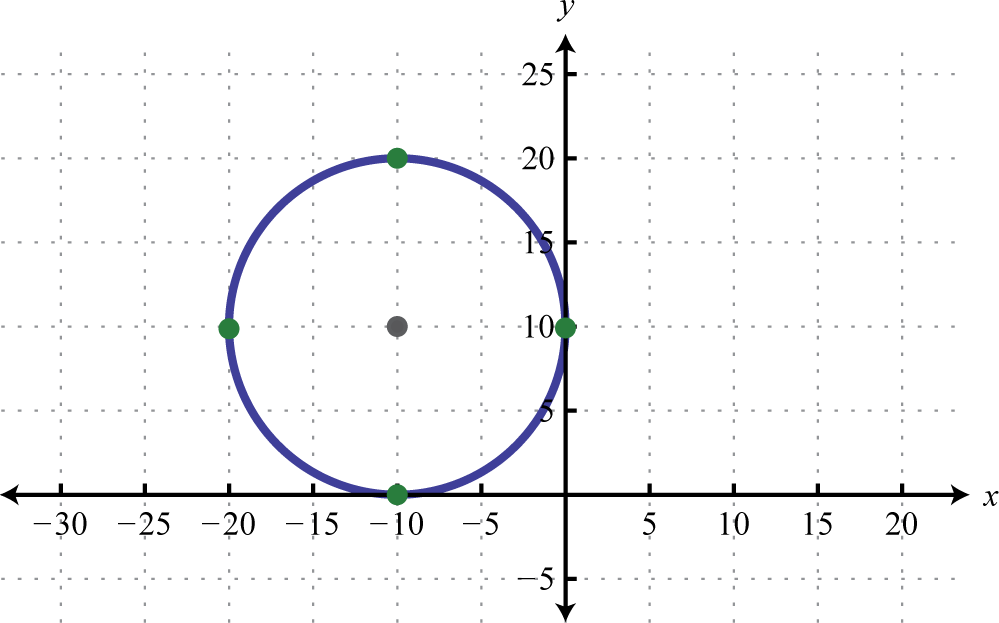
Figura 8.E.35
Ejercicio\(\PageIndex{27}\)
Encuentra los\(x\) - y\(y\) -interceptos.
- \(x=-2(y-4)^{2}+9\)
- \(\frac{(y-1)^{2}}{12}-(x+1)^{2}=1\)
- Contestar
-
1. \(x\)-interceptar:\((-23,0) ; y\) -intercepta:\(\left(0, \frac{8 \pm 3 \sqrt{2}}{2}\right)\)
Ejercicio\(\PageIndex{28}\)
Resolver.
- \(\left\{\begin{array}{l}{x+y=2} \\ {y=-x^{2}+4}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y-x^{2}=-3} \\ {x^{2}+y^{2}=9}\end{array}\right.\)
- \(\left\{\begin{array}{c}{2 x-y=1} \\ {(x+1)^{2}+2 y^{2}=1}\end{array}\right.\)
- \(\left\{\begin{array}{c}{x^{2}+y^{2}=6} \\ {x y=3}\end{array}\right.\)
- Contestar
-
1. \((-1,3),(2,0)\)
3. \(\emptyset\)
Ejercicio\(\PageIndex{29}\)
- Encuentra la ecuación de una elipse en forma estándar con vértices\((−3, −5)\)\((5, −5)\) y un radio menor\(2\) unidades de longitud.
- Encuentra la ecuación de una hipérbola en forma estándar abriendo izquierda y derecha con vértices\((\pm \sqrt{5}, 0)\) y un eje conjugado que mide\(10\) unidades.
- Dada la gráfica de la elipse, determinar su ecuación en forma general.
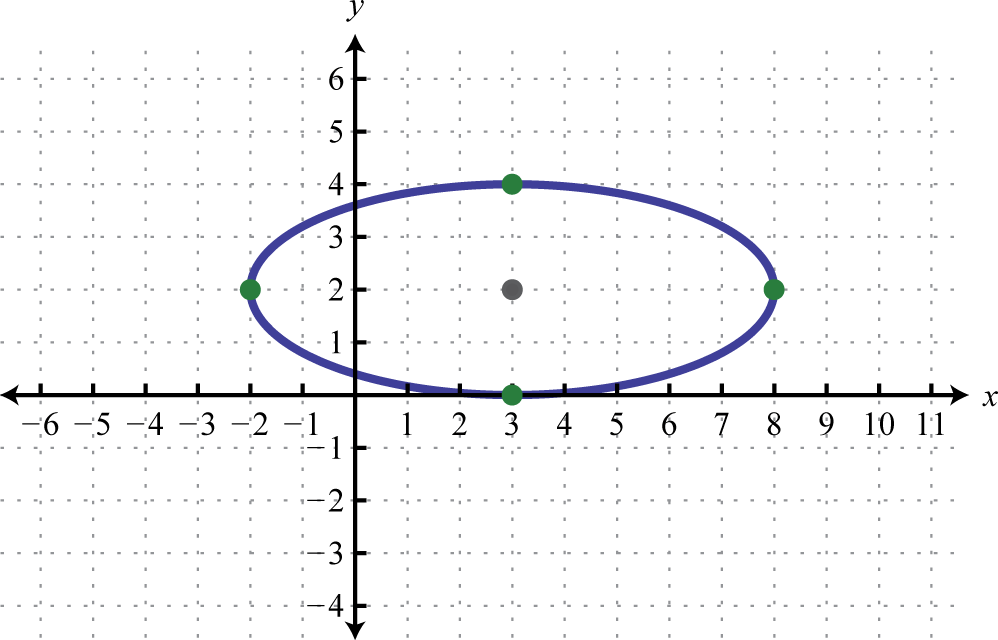
4. Una cubierta rectangular tiene un área de pies\(80\) cuadrados y un perímetro que mide\(36\) pies. Encuentra las dimensiones de la cubierta.
5. La diagonal de un rectángulo mide\(2\sqrt{13}\) centímetros y el perímetro mide\(20\) centímetros. Encuentra las dimensiones del rectángulo.
- Contestar
-
1. \(\frac{(x-1)^{2}}{16}+\frac{(y+5)^{2}}{4}=1\)
3. \(4 x^{2}+25 y^{2}-24 x-100 y+36=0\)
5. \(6\)centímetros por\(4\) centímetros


