8.3: Elipses
- Page ID
- 109911
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Grafica una elipse en forma estándar.
- Determinar la ecuación de una elipse dada su gráfica.
- Reescribe la ecuación de una elipse en forma estándar.
La elipse en forma estándar
Una elipse 14 es el conjunto de puntos en un plano cuyas distancias desde dos puntos fijos, llamados focos, tienen una suma que es igual a una constante positiva. En otras palabras, si los puntos\(F1\) y\(F2\) son los focos (plural de foco) y\(d\) es alguna constante positiva dada entonces\((x,y)\) es un punto en la elipse si\(d=d_{1}+d_{2}\) como se muestra a continuación:
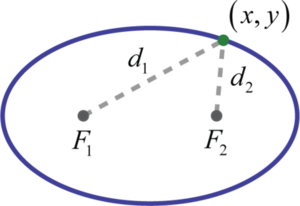
Además, se puede formar una elipse por la intersección de un cono con un plano oblicuo que no es paralelo al lado del cono y no interseca la base del cono. Los puntos en esta forma ovalada donde la distancia entre ellos es máxima se denominan vértices 15 y definen el eje mayor 16. El centro de una elipse es el punto medio entre los vértices. El eje menor 17 es el segmento lineal a través del centro de una elipse definida por dos puntos en la elipse donde la distancia entre ellos es mínima. Los extremos del eje menor se denominan co-vértices 18.
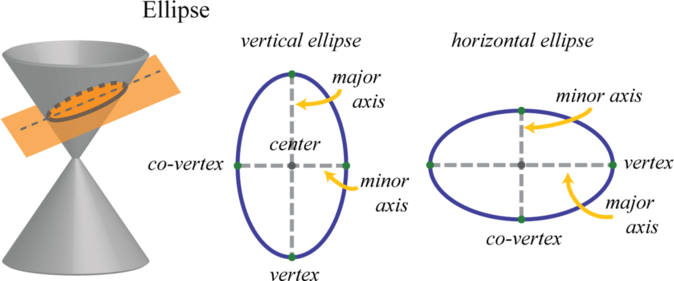
Si el eje mayor de una elipse es paralelo al\(x\) eje -en un plano de coordenadas rectangular, decimos que la elipse es horizontal. Si el eje mayor es paralelo al\(y\) -eje, decimos que la elipse es vertical. En esta sección, sólo nos preocupa bosquejar estos dos tipos de elipses. Sin embargo, la elipse tiene muchas aplicaciones del mundo real y se fomenta la investigación adicional sobre este rico tema. En un plano de coordenadas rectangulares, donde está el centro de una elipse horizontal\((h,k)\), tenemos
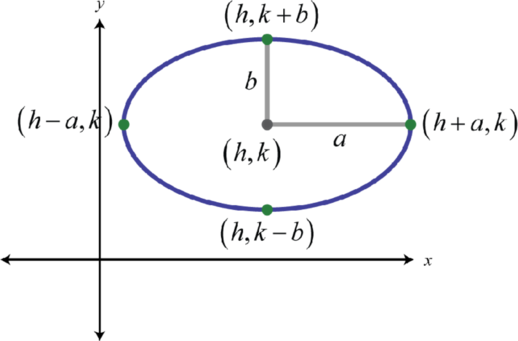
Como se muestra\(a>b\) donde\(a\), la mitad de la longitud del eje mayor, se llama el radio mayor 19. Y\(b\), la mitad de la longitud del eje menor, se llama el radio menor 20. La ecuación de una elipse en forma estándar 21 sigue:
\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)
Los vértices son\((h±a,k)\) y\((h,k±b)\) y la orientación depende de\(a\) y\(b\). Si\(a>b\), entonces la elipse es horizontal como se muestra arriba y si\(a<b\), entonces la elipse es vertical y\(b\) se convierte en el radio mayor. ¿Qué crees que pasa cuando\(a=b\)?
| Ecuación | Centro | \(a\) | \(b\) | Orientación |
|---|---|---|---|---|
| \(\frac{(x-1)^{2}}{4}+\frac{(y-8)^{2}}{9}=1\) | \((1,8)\) | \ (a\)” style="vertical-align:middle; ">\(a=2\) | \ (b\)” style="vertical-align:middle; ">\(b=3\) | Vertical |
| \(\frac{(x-3)^{2}}{2}+\frac{(y+5)^{2}}{16}=1\) | \((3,-5)\) | \ (a\)” style="vertical-align:middle; ">\(a=\sqrt{2}\) | \ (b\)” style="vertical-align:middle; ">\(b=4\) | Vertical |
| \(\frac{(x+1)^{2}}{1}+\frac{(y-7)^{2}}{8}=1\) | \((-1,7)\) | \ (a\)” style="vertical-align:middle; ">\(a=1\) | \ (b\)” style="vertical-align:middle; ">\(b=2 \sqrt{2}\) | Vertical |
| \(\frac{x^{2}}{25}+\frac{(y+6)^{2}}{10}=1\) | \((0,-6)\) | \ (a\)” style="vertical-align:middle; ">\(a=5\) | \ (b\)” style="vertical-align:middle; ">\(b=\sqrt{10}\) | Horizontal |
La gráfica de una elipse está completamente determinada por su centro, orientación, radio mayor y radio menor, todo lo cual se puede determinar a partir de su ecuación escrita en estándar a partir de.
Ejemplo\(\PageIndex{1}\):
Gráfica:\(\frac{(x+3)^{2}}{4}+\frac{(y-2)^{2}}{25}=1\).
Solución
Escrito en esta forma podemos ver que el centro de la elipse es\((−3,2)\),\(a=\sqrt{4}=2\), y\(b=\sqrt{25}=5\). Del centro marca puntos 2 unidades a la izquierda y derecha y 5 unidades arriba y abajo.
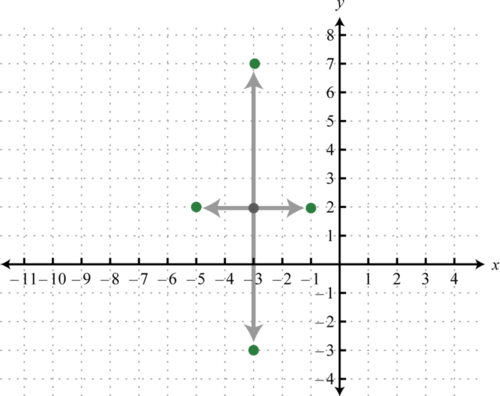
Después dibuja una elipse a través de estos cuatro puntos.
Contestar
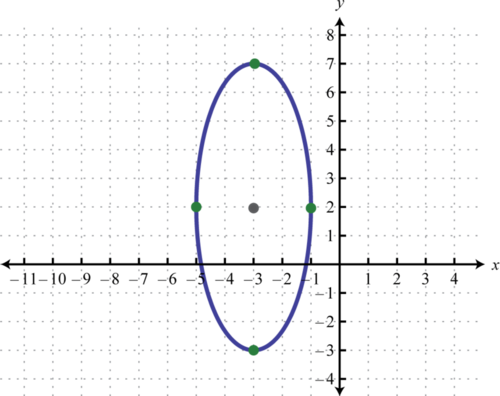
Al igual que con cualquier gráfica, nos interesa encontrar las\(x\) -y\(y\) -intercepciones.
Ejemplo\(\PageIndex{2}\)
Encuentra las intercepciones:\(\frac{(x+3)^{2}}{4}+\frac{(y-2)^{2}}{25}=1\).
Solución
Para encontrar el conjunto\(x\) -intercepts\(y=0\):
\(\begin{aligned} \frac{(x+3)^{2}}{4}+\frac{(0-2)^{2}}{25} &=1 \\ \frac{(x+3)^{2}}{4}+\frac{4}{25} &=1 \\ \frac{(x+3)^{2}}{4} &=1-\frac{4}{25} \\ \frac{(x+3)^{2}}{4} &=\frac{21}{25} \end{aligned}\)
En este punto extraemos la raíz aplicando la propiedad raíz cuadrada.
\(\begin{aligned} \frac{x+3}{2} &=\pm \sqrt{\frac{21}{25}} \\ x+3 &=\pm \frac{2 \sqrt{21}}{5} \\ x &=-3 \pm \frac{2 \sqrt{21}}{5}=\frac{-15 \pm 2 \sqrt{21}}{5} \end{aligned}\)
\(x=0\)Fijando y resolviendo\(y\) leads a soluciones complejas, por lo tanto, no hay\(y\) -intercepciones. Esto se deja como un ejercicio.
Respuesta:
\(x\)-intercepta:\(\left(\frac{-15 \pm 2 \sqrt{21}}{5}, 0\right)\);\(y\) -intercepta: ninguna.
A diferencia de un círculo, la forma estándar para una elipse requiere un\(1\) en un lado de su ecuación.
Ejemplo\(\PageIndex{3}\):
Grafica y etiqueta las intercepciones:\((x-2)^{2}+9(y-1)^{2}=9\).
Solución
Para obtener la forma estándar, con\(1\) en el lado derecho, dividir ambos lados por\(9\).
\(\begin{aligned} \frac{(x-2)^{2}+9(y-1)^{2}}{\color{Cerulean}{9}} &\color{black}{=}\frac{9}{\color{Cerulean}{9}} \\ \frac{(x-2)^{2}}{9}+\frac{9(y-1)^{2}}{9} &=\frac{9}{9} \\ \frac{(x-2)^{2}}{9}+\frac{(y-1)^{2}}{1} &=1 \end{aligned}\)
Por lo tanto, el centro de la elipse es\((2,1)\),\(a=\sqrt{9}=3\), y\(b=\sqrt{1}=1\). El gráfico sigue:
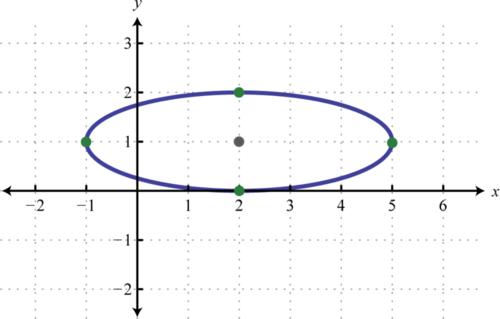
Para encontrar las intercepciones podemos usar el formulario estándar\(\frac{(x-2)^{2}}{9}+(y-1)^{2}=1\):
| \(x\)-intercepta conjunto\(y=0\) | \(y\)-intercepta conjunto\(x=0\) |
| \(\begin{array}{r}{\frac{(x-2)^{2}}{9}+(\color{Cerulean}{0}\color{black}{-}1)^{2}=1} \\ {\frac{(x-2)^{2}}{9}+1=1} \\ {(x-2)^{2}=0} \\ {x-2=0} \\ {x=2}\end{array}\) | \(\begin{aligned} \frac{(\color{Cerulean}{0}\color{black}{-}2)^{2}}{9}+(y-1)^{2} &=1 \\ \frac{4}{9}+(y-1)^{2} &=1 \\(y-1)^{2} &=\frac{5}{9} \\ y-1 &=\pm \sqrt{\frac{5}{9}} \\ y &=1 \pm \frac{\sqrt{5}}{3}=\frac{3 \pm \sqrt{5}}{3} \end{aligned}\) |
Por lo tanto la\(x\) -intercepción es\((2,0)\) y las\(y\) -intercepciones son\(\left(0, \frac{3+\sqrt{5}}{3}\right)\) y\(\left(0, \frac{3-\sqrt{5}}{3}\right)\).
Respuesta:
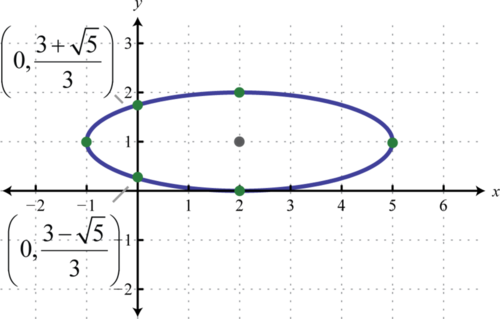
Considera la elipse centrada en el origen,
\(x^{2}+\frac{y^{2}}{4}=1\)
Dada esta ecuación podemos escribir,
\(\frac{(x-0)^{2}}{1^{2}}+\frac{(y-0)^{2}}{2^{2}}=1\)
En esta forma, es claro que el centro es\((0,0)\),\(a=1\), y\(b=2\). Además, si resolvemos para\(y\) obtenemos dos funciones:
\(\begin{aligned} x^{2}+\frac{y^{2}}{4} &=1 \\ \frac{y^{2}}{4} &=1-x^{2} \\ y^{2} &=4\left(1-x^{2}\right) \\ y &=\pm \sqrt{4\left(1-x^{2}\right)} \\ y &=\pm 2 \sqrt{1-x^{2}} \end{aligned}\)
La función definida por\(y=2 \sqrt{1-x^{2}}\) es la mitad superior de la elipse y la función definida por\(y=-2 \sqrt{1-x^{2}}\) es la mitad inferior.
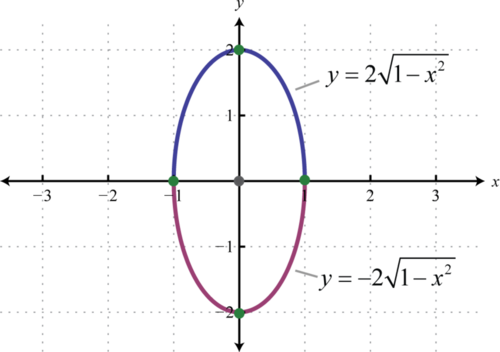
Ejercicio\(\PageIndex{1}\)
Gráfica:\(9(x-3)^{2}+4(y+2)^{2}=36\).
- Contestar
-
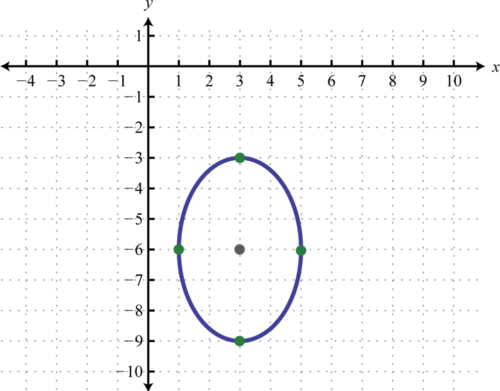
Figura\(\PageIndex{9}\)
La elipse en forma general
Hemos visto que la gráfica de una elipse está completamente determinada por su centro, orientación, radio mayor y radio menor; que se puede leer de su ecuación en forma estándar. Sin embargo, la ecuación no siempre se da en forma estándar. La ecuación de una elipse en forma general 22 sigue:
\(p x^{2}+q y^{2}+c x+d y+e=0\)
donde\(p,q>0\). Los pasos para graficar una elipse dada su ecuación en forma general se describen en el siguiente ejemplo.
Ejemplo\(\PageIndex{4}\):
Gráfica\(2 x^{2}+9 y^{2}+16 x-90 y+239=0\).
Solución
Comience por reescribir la ecuación en forma estándar.
Paso 1: Agrupar los términos con las mismas variables y mover la constante hacia el lado derecho. Factor para que el coeficiente principal de cada agrupación sea\(1\).
\(\begin{aligned} 2 x^{2}+9 y^{2}+16 x-90 y+239 &=0 \\ \left(2 x^{2}+16 x+\_\_\_\right.)+\left(9 y^{2}-90 y+\_\_\_\right)&=-239 \\ 2\left(x^{2}+8x+\_\_\_ \right)+9\left(y^{2}-10y+\_\_\_ \right)&=-239 \end{aligned}\)
Paso 2: Completar el cuadrado para cada agrupación. En este caso, para los términos que impliquen\(x\) uso\(\left(\frac{8}{2}\right)^{2}=4^{2}=16\) y para los términos que impliquen\(y\) uso\(\left(\frac{-10}{2}\right)^{2}=(-5)^{2}=25\). El factor frente a la agrupación afecta el valor utilizado para equilibrar la ecuación en el lado derecho:
\(2\color{black}{\left(x^{2}+8 x\color{Cerulean}{+16}\right)+}9\color{black}{\left(y^{2}-10 y\color{OliveGreen}{+25}\right)=}-239\color{Cerulean}{+32}\color{OliveGreen}{+225}\)
Debido a la propiedad distributiva, agregar\(16\) dentro de la primera agrupación equivale a agregar\(2⋅16=32\). De igual manera, agregar\(25\) dentro de la segunda agrupación equivale a sumar\(9⋅25=225\). Ahora factor y luego dividir para obtener\(1\) en el lado derecho.
\(\begin{aligned}2(x+4)^{2}+9(y-5)^{2}&=18 \\ \frac{2(x+4)^{2}+9(y-5)^{2}}{\color{Cerulean}{18}}&\color{black}{=}\frac{18}{\color{Cerulean}{18}} \\ \frac{2(x+4)^{2}}{18}+\frac{9(y-5)^{2}}{18}&=\frac{18}{18} \\ \frac{(x+4)^{2}}{9}+\frac{(y-5)^{2}}{2}&=1\end{aligned}\)
Paso 3: Determinar el centro,\(a\), y\(b\). En este caso, el centro es\((−4,5)\),\(a=\sqrt{9}=3\), y\(b=\sqrt{2}\).
Paso 4: Usa a para marcar los vértices a la izquierda y derecha del centro, usa b para marcar los vértices arriba y abajo desde el centro, y luego bosquejar la gráfica. En este caso, los vértices a lo largo de los ejes menores no\((-4,5 \pm \sqrt{2})\) son aparentes y deben ser etiquetados.
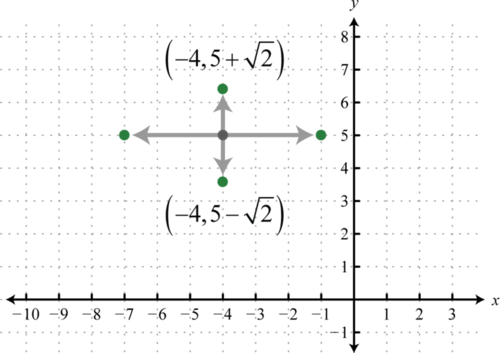
Respuesta:

Ejemplo\(\PageIndex{5}\):
Determinar el centro de la elipse así como las longitudes de los ejes mayor y menor:\(5 x^{2}+y^{2}-3 x+40=0\).
Solución
En este ejemplo, sólo necesitamos completar el cuadrado para los términos que implican\(x\).
\(\begin{aligned} 5 x^{2}+y^{2}-30 x+40 &=0 \\ \left(5 x^{2}-30 x+ \_\_\_\right)+y^{2}&=-40 \\5\left(x^{2}-6x+\_\_\_ \right)+y^{2}&=-40 \end{aligned}\)
Utilízalo\(\left(\frac{-6}{2}\right)^{2}=(-3)^{2}=9\) para que la primera agrupación sea balanceada por\(5⋅9=45\) en el lado derecho.
\(\begin{aligned} 5\color{black}{\left(x^{2}-6 x\color{Cerulean}{+9}\right)+}y^{2} &=-40\color{Cerulean}{+45} \\ 5(x-3)^{2}+y^{2} &=5 \\ \frac{5(x-3)^{2}+y^{2}}{\color{Cerulean}{5}} &\color{black}{=}\frac{5}{\color{Cerulean}{5}} \\ \frac{(x-3)^{2}}{1}+\frac{y^{2}}{5} &=1 \end{aligned}\)
Aquí, el centro es\((3,0)\),\(a=\sqrt{1}=1\), y\(b=\sqrt{5}\). Porque\(b\) es mayor que\(a\), la longitud del eje mayor es\(2b\) y la longitud del eje menor es\(2a\).
Contestar
Centro:\((3,0)\); eje mayor: 2\(\sqrt{5}\) unidades; eje menor:\(2\) unidades.
Ejercicio\(\PageIndex{2}\)
Gráfica\(x^{2}+4 y^{2}+10 x-16 y+25=0\).
- Contestar
-
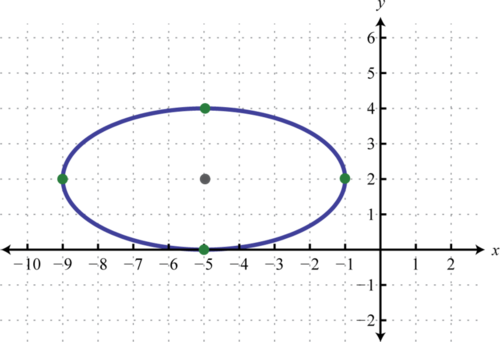
Figura\(\PageIndex{12}\) www.youtube.com/v/mhp7s5h2820
Claves para llevar
- La gráfica de una elipse está completamente determinada por su centro, orientación, radio mayor y radio menor.
- El centro, orientación, radio mayor, y el radio menor son evidentes si la ecuación de una elipse se da en forma estándar:\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\).
- Para graficar una elipse, marca puntos\(a\) unidades izquierda y derecha desde el centro y puntos\(b\) unidades arriba y abajo desde el centro. Dibuja una elipse a través de estos puntos.
- La orientación de una elipse está determinada por\(a\) y\(b\). Si\(a>b\) entonces la elipse es más ancha que alta y se considera una elipse horizontal. Si a<ba<b entonces la elipse es más alta que ancha y se considera una elipse vertical.
- Si la ecuación de una elipse se da en forma general\(p x^{2}+q y^{2}+c x+d y+e=0\) donde\(p,q>0\), agrupe los términos con las mismas variables, y complete el cuadrado para ambas agrupaciones.
- Reconocemos la ecuación de una elipse si es cuadrática en ambas\(x\) y\(y\) y los coeficientes de cada término cuadrado tienen el mismo signo.
Ejercicio\(\PageIndex{3}\)
Dada la ecuación de una elipse en forma estándar, determine su centro, orientación, radio mayor y radio menor.
- \(\frac{(x-1)^{2}}{4}+\frac{(y+2)^{2}}{49}=1\)
- \(\frac{(x+3)^{2}}{64}+\frac{(y-2)^{2}}{9}=1\)
- \(\frac{x^{2}}{3}+(y+9)^{2}=1\)
- \(\frac{(x-1)^{2}}{8}+y^{2}=1\)
- \(4(x+5)^{2}+9(y+5)^{2}=36\)
- \(16(x-1)^{2}+3(y+10)^{2}=48\)
- Contestar
-
1. Centro:\((1, −2)\); orientación: vertical; radio mayor:\(7\) unidades; radio menor:\(2\) unidades;\(a = 2; b = 7\)
3. Centro:\((0, −9)\); orientación: horizontal; radio mayor:\(\sqrt{3}\) unidades; radio menor:\(1\) unidad;\(a=\sqrt{3} ; b=1\)
5. Centro:\((−5, −5)\); orientación: horizontal; radio mayor:\(3\) unidades; radio menor:\(2\) unidades;\(a = 3; b = 2\)
Ejercicio\(\PageIndex{4}\)
Determinar la forma estándar para la ecuación de una elipse dada la siguiente información.
- Centro\((3,4)\) con\(a=5\) y\(b=2\).
- Centro\((-1,9)\) con\(a=7\) y\(b=3\).
- Centro\((5,-1)\) con\(a=\sqrt{6}\) y\(b=2 \sqrt{3}\).
- Centro\((-7,-2)\) con\(a=5 \sqrt{2}\) y\(b=\sqrt{7}\).
- Centro\((0,-3)\) con\(a=1\) y\(b=\sqrt{5}\).
- Centro\((0,0)\) con\(a=\sqrt{2}\) y\(b=4\).
- Contestar
-
1. \(\frac{(x-3)^{2}}{25}+\frac{(y-4)^{2}}{4}=1\)
3. \(\frac{(x-5)^{2}}{6}+\frac{(y+1)^{2}}{12}=1\)
5. \(x^{2}+\frac{(y+3)^{2}}{5}=1\)
Ejercicio\(\PageIndex{5}\)
Gráfica.
- \(\frac{(x-4)^{2}}{4}+\frac{(y+2)^{2}}{9}=1\)
- \(\frac{(x+1)^{2}}{25}+\frac{(y-2)^{2}}{4}=1\)
- \(\frac{(x-5)^{2}}{16}+\frac{(y+6)^{2}}{1}=1\)
- \(\frac{(x+4)^{2}}{4}+\frac{(y+3)^{2}}{36}=1\)
- \(\frac{(x-2)^{2}}{9}+\frac{(y-1)^{2}}{64}=1\)
- \(\frac{(x+1)^{2}}{49}+(y+3)^{2}=1\)
- \(4(x+3)^{2}+9(y-3)^{2}=36\)
- \(16 x^{2}+(y-1)^{2}=16\)
- \(4(x-2)^{2}+25 y^{2}=100\)
- \(81 x^{2}+y^{2}=81\)
- \(\frac{(x-2)^{2}}{8}+\frac{(y-4)^{2}}{9}=1\)
- \(\frac{(x+1)^{2}}{4}+\frac{(y-1)^{2}}{12}=1\)
- \(\frac{(x-6)^{2}}{2}+\frac{(y+2)^{2}}{5}=1\)
- \(\frac{(x+3)^{2}}{18}+\frac{(y-5)^{2}}{3}=1\)
- \(3 x^{2}+2(y-3)^{2}=6\)
- \(5(x+1)^{2}+3 y^{2}=15\)
- \(4 x^{2}+6 y^{2}=24\)
- \(5 x^{2}+10 y^{2}=50\)
- Contestar
-
1.
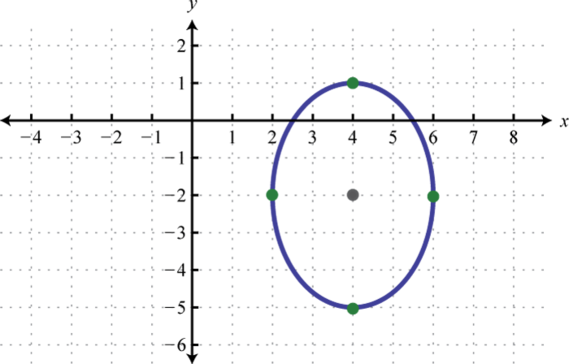
Figura\(\PageIndex{13}\) 3.
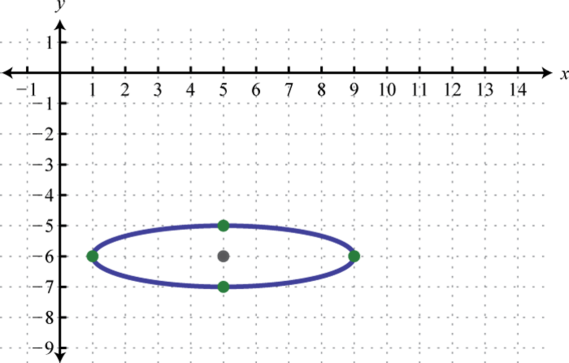
Figura\(\PageIndex{14}\) 5.

Figura\(\PageIndex{15}\) 7.
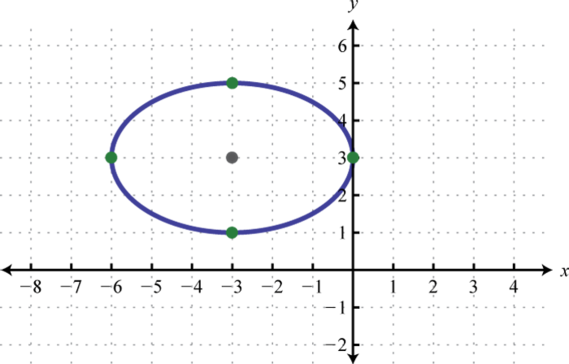
Figura\(\PageIndex{16}\) 9.

Figura\(\PageIndex{17}\) 11.
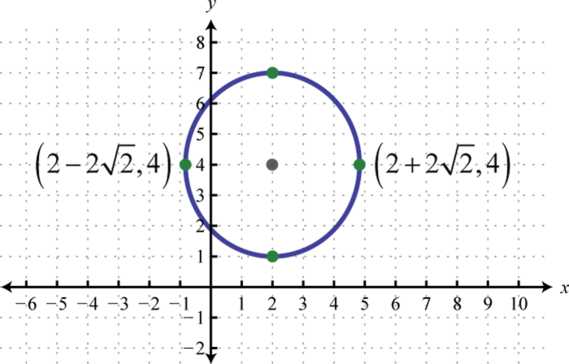
Figura\(\PageIndex{18}\) 13.
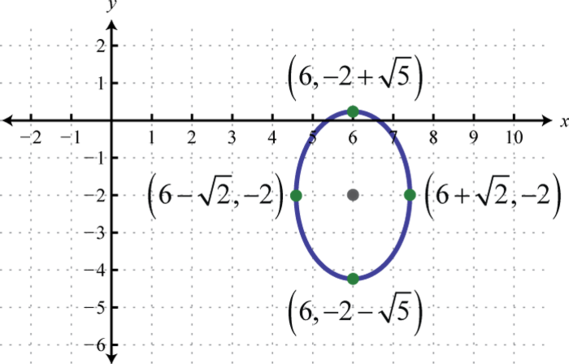
Figura\(\PageIndex{19}\) 15.

Figura\(\PageIndex{20}\) 17.
Figura\(\PageIndex{21}\)
Ejercicio\(\PageIndex{6}\)
Encuentra las\(x\) - y\(y\) -intercepciones.
- \(\frac{(x-3)^{2}}{4}+\frac{(y-2)^{2}}{9}=1\)
- \(\frac{(x+3)^{2}}{16}+\frac{(y-7)^{2}}{9}=1\)
- \(\frac{(x-2)^{2}}{4}+\frac{(y+6)^{2}}{36}=1\)
- \(\frac{(x+1)^{2}}{25}+\frac{(y-1)^{2}}{9}=1\)
- \(5 x^{2}+2(y-4)^{2}=20\)
- \(4(x-3)^{2}+9 y^{2}=72\)
- \(5 x^{2}+2 y^{2}=10\)
- \(3 x^{2}+4 y^{2}=24\)
- Contestar
-
1. \(x\)-intercepta:\(\left(\frac{9 \pm 2 \sqrt{5}}{3}, 0\right)\);\(y\) -intercepta: ninguna
3. \(x\)-intercepta:\((2,0)\);\(y\) -intercepta:\((0,-6\)
5. \(x\)-intercepta: ninguno;\(y\) -intercepta:\((0,4 \pm \sqrt{10})\)
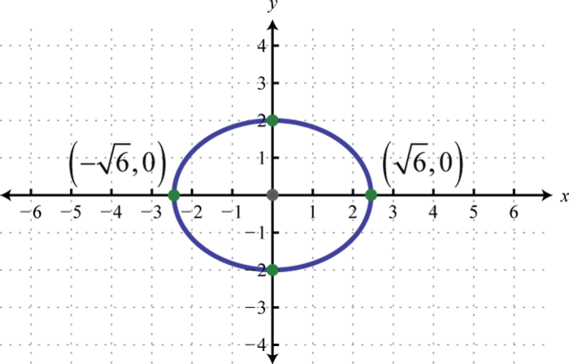
7. \(x\)-intercepta:\((\pm \sqrt{2}, 0)\);\(y\) -intercepta:\((0, \pm \sqrt{5})\)
Ejercicio\(\PageIndex{7}\)
Encuentra la ecuación de la elipse.
- Elipse con vértices\((±5, 0)\) y\((0, ±6)\).
- Elipse cuyo eje mayor tiene vértices\((2, 9)\) y\((2, −1)\) y eje menor tiene vértices\((−2, 4)\) y\((6, 4)\).
- Elipse cuyo eje mayor tiene vértices\((−8, −2)\)\((0, −2)\) y el eje menor tiene una longitud de\(4\) unidades.
- Elipse cuyo eje mayor tiene vértices\((−2, 2)\)\((−2, 8)\) y el eje menor tiene una longitud de\(2\) unidades.
- Contestar
-
1. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
3. \(\frac{(x+4)^{2}}{16}+\frac{(y+2)^{2}}{4}=1\)
Ejercicio\(\PageIndex{8}\)
Reescribir en forma estándar y gráfica.
- \(4 x^{2}+9 y^{2}+8 x-36 y+4=0\)
- \(9 x^{2}+25 y^{2}-18 x+100 y-116=0\)
- \(4 x^{2}+49 y^{2}+24 x+98 y-111=0\)
- \(9 x^{2}+4 y^{2}-72 x+24 y+144=0\)
- \(x^{2}+64 y^{2}-12 x+128 y+36=0\)
- \(16 x^{2}+y^{2}-96 x-4 y+132=0\)
- \(36 x^{2}+4 y^{2}-40 y-44=0\)
- \(x^{2}+9 y^{2}-2 x-8=0\)
- \(x^{2}+9 y^{2}-4 x-36 y-41=0\)
- \(16 x^{2}+y^{2}+160 x-10 y+361=0\)
- \(4 x^{2}+5 y^{2}+32 x-20 y+64=0\)
- \(2 x^{2}+3 y^{2}-8 x-30 y+65=0\)
- \(8 x^{2}+5 y^{2}-16 x+10 y-27=0\)
- \(7 x^{2}+2 y^{2}+28 x-16 y+46=0\)
- \(36 x^{2}+16 y^{2}-36 x-32 y-119=0\)
- \(16 x^{2}+100 y^{2}+64 x-300 y-111=0\)
- \(x^{2}+4 y^{2}-20 y+21=0\)
- \(9 x^{2}+y^{2}+12 x-2 y-4=0\)
- Contestar
-
1. \(\frac{(x+1)^{2}}{9}+\frac{(y-2)^{2}}{4}=1\);
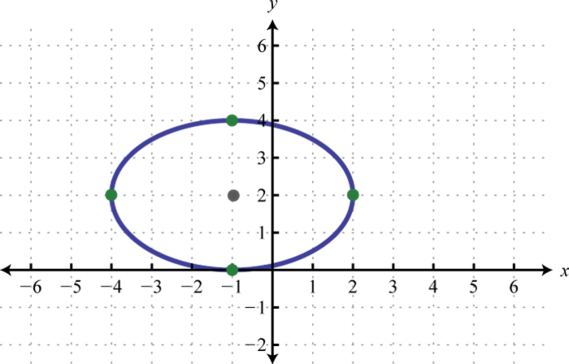
Figura\(\PageIndex{22}\) 3. \(\frac{(x+3)^{2}}{49}+\frac{(y+1)^{2}}{4}=1\);
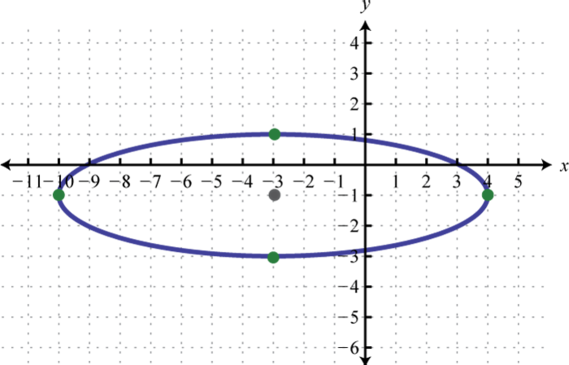
Figura\(\PageIndex{23}\) 5. \(\frac{(x-6)^{2}}{64}+(y+1)^{2}=1\);
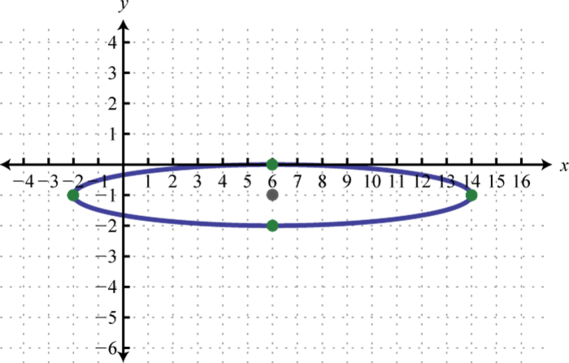
Figura\(\PageIndex{24}\) 7. \(\frac{x^{2}}{4}+\frac{(y-5)^{2}}{36}=1\);
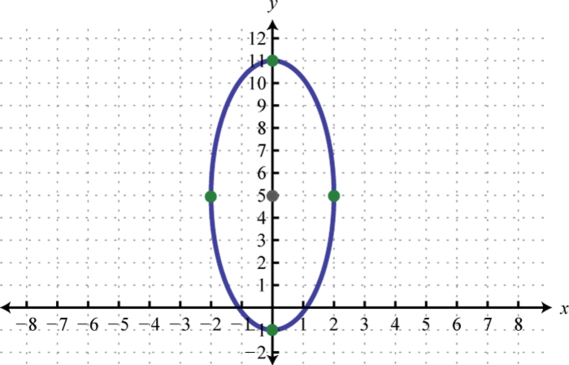
Figura\(\PageIndex{25}\) 9. \(\frac{(x-2)^{2}}{81}+\frac{(y-2)^{2}}{9}=1\);
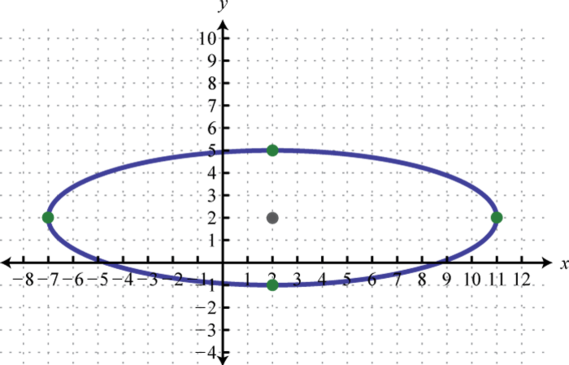
Figura\(\PageIndex{26}\) 11. \(\frac{(x+4)^{2}}{5}+\frac{(y-2)^{2}}{4}=1\);
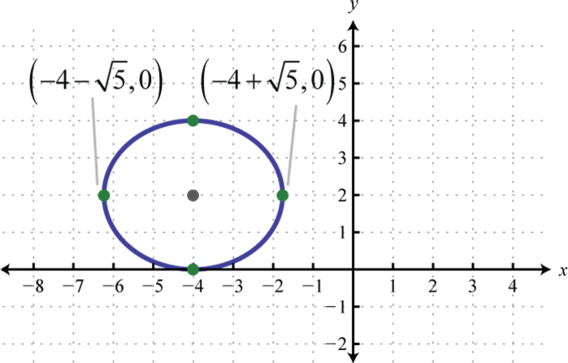
Figura\(\PageIndex{27}\) 13. \(\frac{(x-1)^{2}}{5}+\frac{(y+1)^{2}}{8}=1\);

Figura\(\PageIndex{28}\) 15. \(\frac{\left(x-\frac{1}{2}\right)^{2}}{4}+\frac{(y-1)^{2}}{9}=1\);
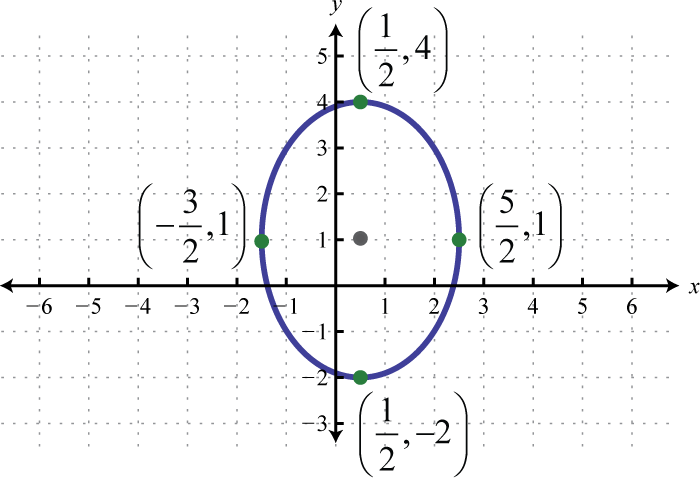
Figura\(\PageIndex{29}\) 17. \(\frac{x^{2}}{4}+\left(y-\frac{5}{2}\right)^{2}=1\);

Figura\(\PageIndex{30}\)
Ejercicio\(\PageIndex{9}\)
Dada la forma general determinar las intercepciones.
- \(5 x^{2}+4 y^{2}-20 x+24 y+36=0\)
- \(4 x^{2}+3 y^{2}-8 x+6 y-5=0\)
- \(6 x^{2}+y^{2}-12 x+4 y+4=0\)
- \(8 x^{2}+y^{2}-6 y-7=0\)
- \(5 x^{2}+2 y^{2}-20 x-8 y+18=0\)
- \(2 x^{2}+3 y^{2}-4 x-5 y+1=0\)
- Contestar
-
1. \(x\)-intercepta: ninguno;\(y\) -intercepta:\((0,-3)\)
3. \(x\)-intercepta:\(\left(\frac{3 \pm \sqrt{3}}{3}, 0\right)\);\(y\) -intercepta:\((0,-2)\)
5. \(x\)-intercepta:\(\left(\frac{10 \pm \sqrt{10}}{5}, 0\right)\);\(y\) -intercepta: ninguna
Ejercicio\(\PageIndex{10}\)
Determinar el área de la elipse. (El área de una elipse viene dada por la fórmula\(A = πab\), donde\(a\) y\(b\) son las longitudes del radio mayor y el radio menor).
- \(\frac{(x-10)^{2}}{25}+\frac{(y+3)^{2}}{5}=1\)
- \(\frac{(x+1)^{2}}{18}+\frac{y^{2}}{36}=1\)
- \(7 x^{2}+3 y^{2}-14 x+36 y+94=0\)
- \(4 x^{2}+8 y^{2}+20 x-8 y+11=0\)
- Contestar
-
1. \(5\pi \sqrt{5}\)unidades cuadradas
3. \(\pi \sqrt{21}\)unidades cuadradas
Ejercicio\(\PageIndex{11}\)
Dada la gráfica de una elipse, determinar su ecuación en forma general.
1.
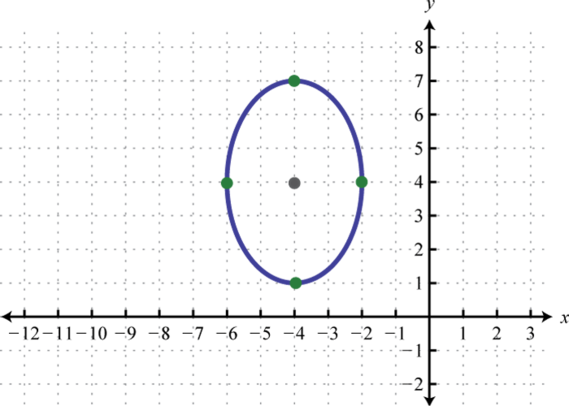
2.
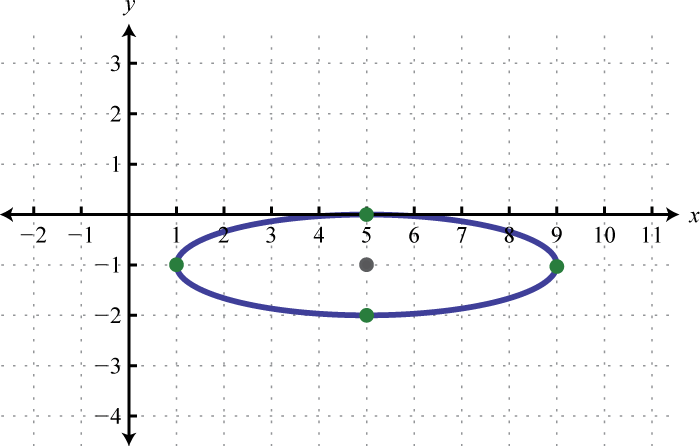
3.
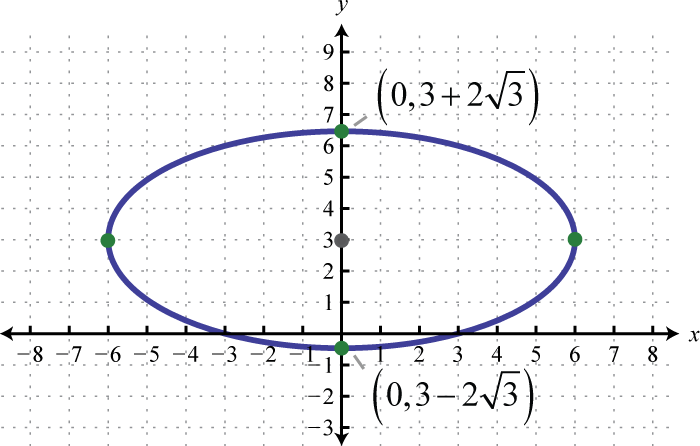
4.
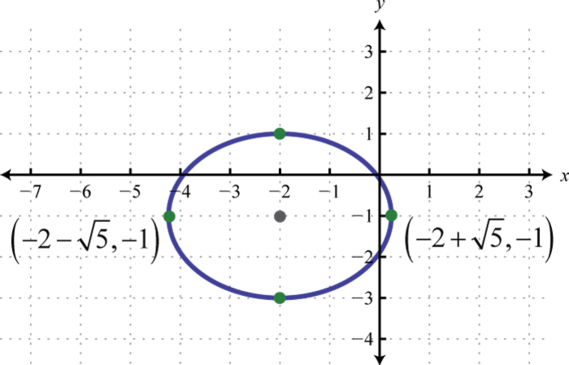
- Contestar
-
1. \(9 x^{2}+4 y^{2}+72 x-32 y+172=0\)
3. \(x^{2}+3 y^{2}-18 y-9=0\)
Ejercicio\(\PageIndex{12}\)
- Explica por qué un círculo puede ser considerado como una elipse muy especial.
- Haz tu propia ecuación de elipse, escríbalo en forma general y gráficalo.
- ¿Todas las elipses tienen intercepciones? ¿Cuáles son los posibles números de intercepciones para una elipse? Explique.
- Investigue y discuta ejemplos reales de elipses.
- Contestar
-
1. La respuesta puede variar
3. La respuesta puede variar
Notas al pie
14 El conjunto de puntos en un plano cuyas distancias desde dos puntos fijos tienen una suma que es igual a una constante positiva.
15 Puntos en la elipse que marcan los puntos finales del eje mayor.
16 El segmento de línea a través del centro de una elipse definida por dos puntos en la elipse donde la distancia entre ellos es máxima.
17 El segmento de línea a través del centro de una elipse definida por dos puntos en la elipse donde la distancia entre ellos es mínima.
18 Puntos en la elipse que marcan los extremos del eje menor.
19 La mitad de la longitud del eje mayor.
20 La mitad de la longitud del eje menor.
21 La ecuación de una elipse escrita en la\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) forma.El centro es\((h, k)\) y el mayor de\(a\) y\(b\) es el radio mayor y el menor es el radio menor.
22 La ecuación de una elipse escrita en la forma\(p x^{2}+q y^{2}+c x+d y+e=0\) donde\(p, q > 0\).


