8.5: Resolviendo sistemas no lineales

Última actualización
Guardar como PDF

Page ID: 109917

Anonymous
LibreTexts

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Objetivos de aprendizaje

Identificar sistemas no lineales.
Resolver sistemas no lineales utilizando el método de sustitución.

Sistemas no lineales

Un sistema de ecuaciones donde al menos una ecuación no es lineal se denomina sistema no lineal ³². En esta sección utilizaremos el método de sustitución para resolver sistemas no lineales. Recordemos que las soluciones a un sistema con dos variables son pares ordenados\((x,y)\) que satisfacen ambas ecuaciones.

Ejemplo\(\PageIndex{1}\):

Resolver:\(\left\{\begin{array}{l}{x+2 y=0} \\ {x^{2}+y^{2}=5}\end{array}\right.\).

Solución

En este caso comenzamos resolviendo para x en la primera ecuación.

\(\left\{\begin{array}{c}{x+2 y=0} \\ {x^{2}+y^{2}=5}\end{array}\Longrightarrow x=-2y \right.\)

Sustituir\(x=−2y\) en la segunda ecuación y luego resolver para\(y\).

\(\begin{aligned}(\color{Cerulean}{-2y }\color{black}{)}^{2}+y^{2} &=5 \\ 4 y^{2}+y^{2} &=5 \\ 5 y^{2} &=5 \\ y^{2} &=1 \\ y &=\pm 1 \end{aligned}\)

Aquí hay dos respuestas para\(y\);\(x=−2y\) utilízalo para encontrar los\(x\) valores -correspondientes.

Mesa\(\PageIndex{1}\)
Usando\(y=-1\)	Usando\(y=1\)
\ (y=-1\) ">\(\begin{aligned} x &=-2 y \\ &=-2(-1) \\ &=2 \end{aligned}\)	\ (y=1\) ">\(\begin{aligned} x &=-2 y \\ &=-2(1) \\ &=-2 \end{aligned}\)

Esto nos da dos soluciones de par ordenadas,\((2,−1)\) y\((−2,1)\).

Respuesta:

\((2,−1), (−2,1)\)

En el ejemplo anterior, el sistema dado consistía en una línea y un círculo. Graficando estas ecuaciones en el mismo conjunto de ejes, podemos ver que las dos soluciones de pares ordenados corresponden a los dos puntos de intersección.

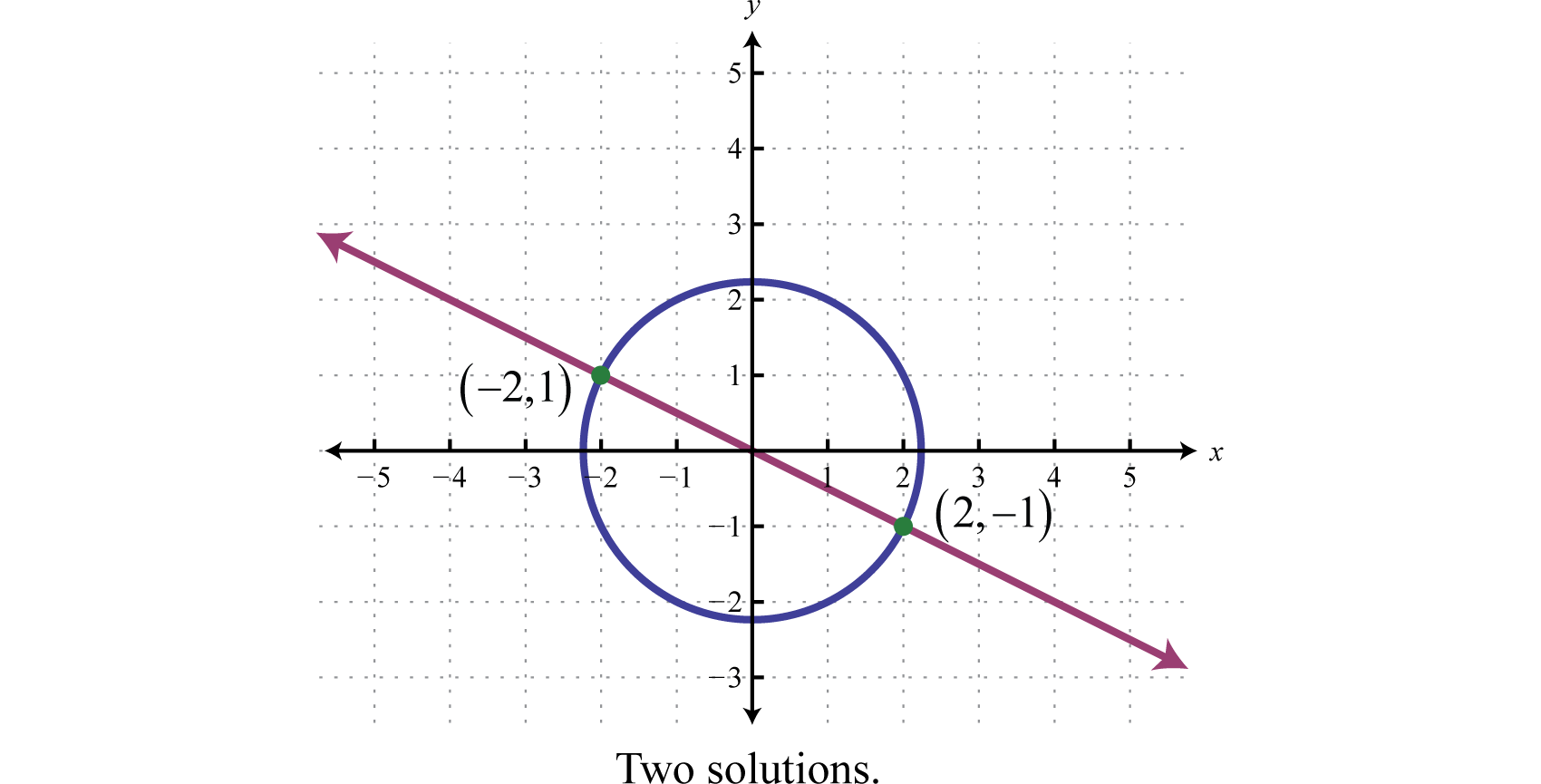
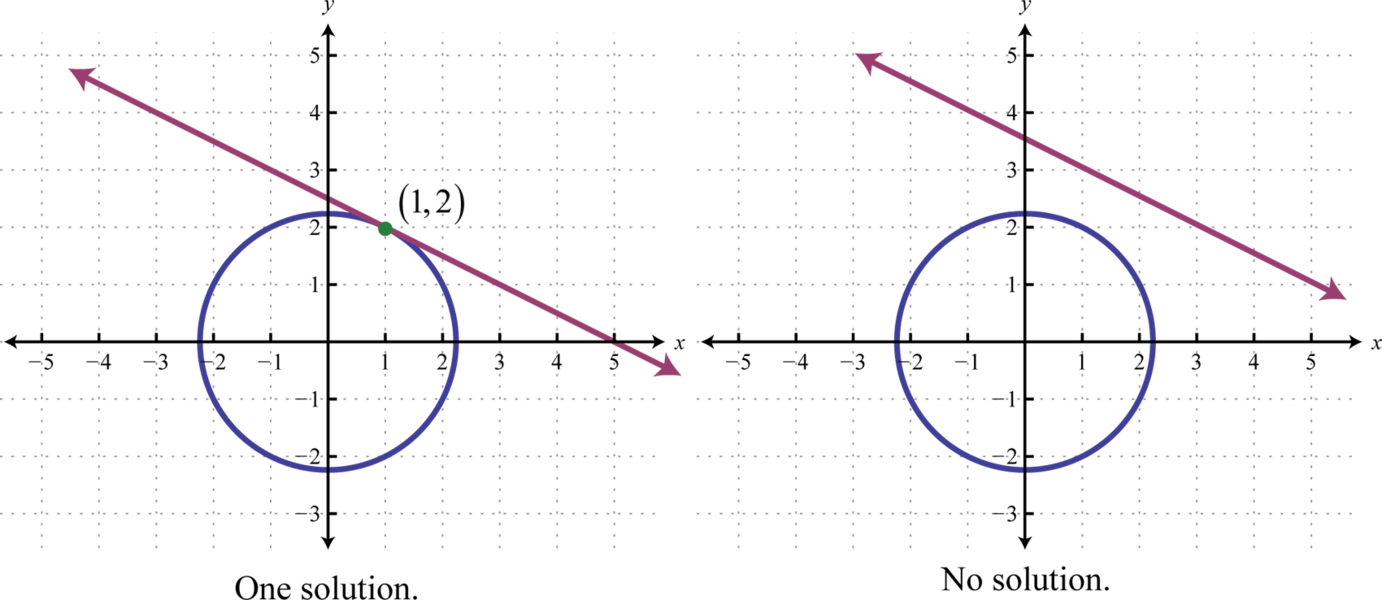
Si se nos da un sistema que consiste en un círculo y una línea, entonces hay\(3\) posibilidades de soluciones reales: dos soluciones como se muestra arriba, una solución o ninguna solución.

Ejemplo\(\PageIndex{2}\)

Resolver:\(\left\{\begin{array}{c}{x+y=3} \\ {x^{2}+y^{2}=2}\end{array}\right.\).

Solución

Resuelve para\(y\) en la primera ecuación.

\(\left\{\begin{array}{c}{x+y} \\ {x^{2}+y^{2}}\end{array}\right.\)

A continuación, sustituya\(y=3−x\) en la segunda ecuación y luego resuelva para\(x\).

\(\begin{array}{r}{x^{2}+(\color{Cerulean}{3-x}\color{black}{)}^{2}=2} \\ {x^{2}+9-6 x+x^{2}=2} \\ {2 x^{2}-6 x+9=2} \\ {2 x^{2}-6 x+7=0}\end{array}\)

La ecuación resultante no factoriza. Además, usando\(a=2\),\( b=−6\), y\(c=7\) podemos ver que el discriminante es negativo:

\(\begin{aligned} b^{2}-4 a c &=(-6)^{2}-4(2)(7) \\ &=36-56 \\ &=-20 \end{aligned}\)

Concluimos que no hay soluciones reales a esta ecuación y, por lo tanto, no hay solución para el sistema.

Respuesta:

\(Ø\)

Ejercicio\(\PageIndex{1}\)

Resolver:\(\left\{\begin{aligned} x-y &=5 \\ x^{2}+(y+1)^{2} &=8 \end{aligned}\right.\)

Responder

\((2,−3)\)

www.youtube.com/V/ToirJW-8sna

Si se le da un círculo y una parábola, entonces hay\(5\) posibilidades de soluciones.

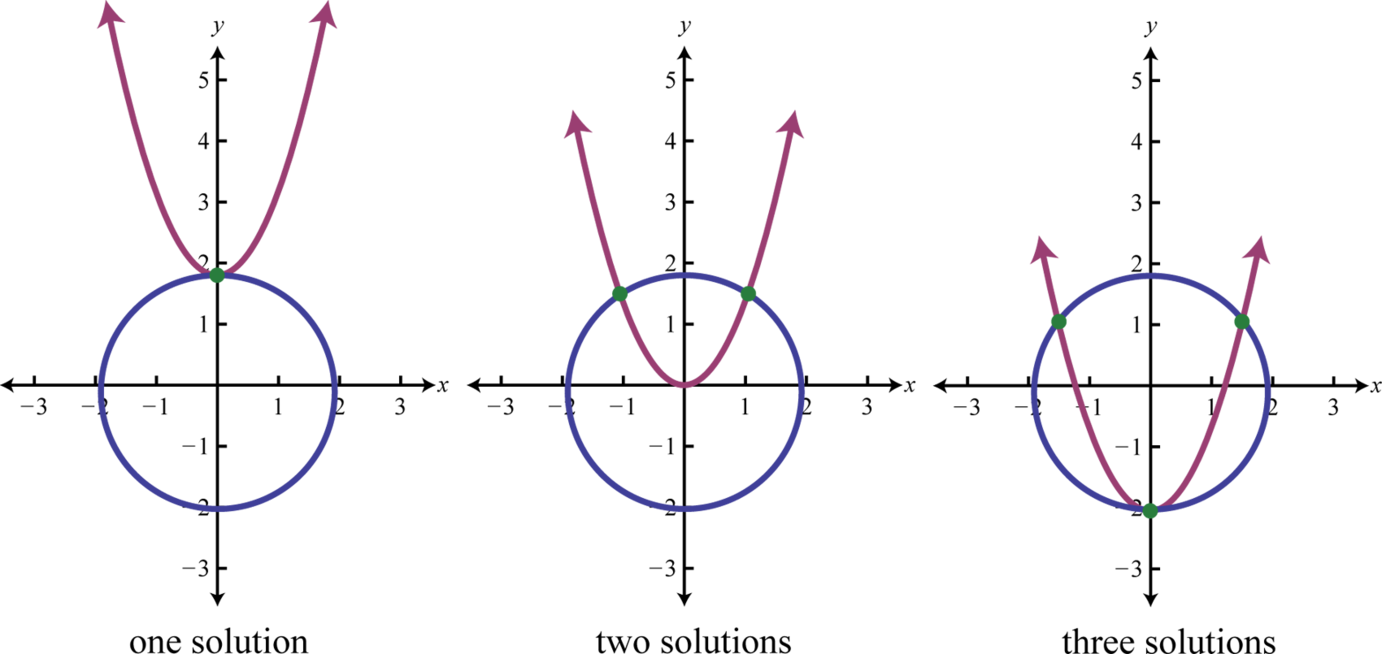
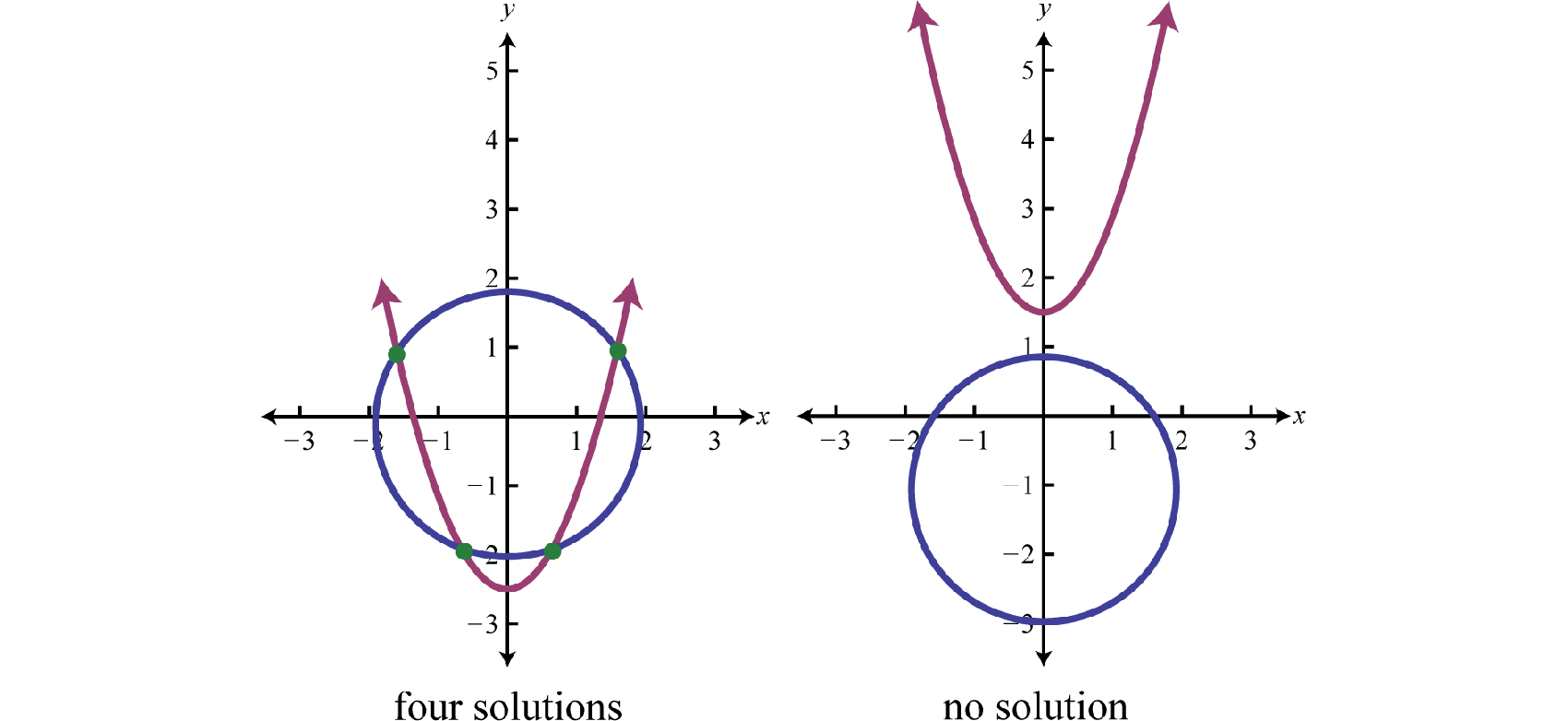
Al usar el método de sustitución, podemos realizar el paso de sustitución usando expresiones algebraicas completas. El objetivo es producir una sola ecuación en una variable que pueda resolverse utilizando las técnicas aprendidas hasta este punto en nuestro estudio del álgebra.

Ejemplo\(\PageIndex{3}\):

Resolver:\(\left\{\begin{array}{c}{x^{2}+y^{2}=2} \\ {y-x^{2}=-2}\end{array}\right.\).

Solución

Podemos resolver para\(x^{2}\) en la segunda ecuación.

\(\left\{\begin{array}{l}{x^{2}+y^{2}=2} \\ {y-x^{2}=-2 \quad \Rightarrow \quad y+2=x^{2}}\end{array}\right.\)

Sustituir\(x^{2}=y+2\) en la primera ecuación y luego resolver para\(y\).

\(\begin{aligned} \color{Cerulean}{y+2}\color{black}{+}y^{2} &=2 \\ y^{2}+y &=0 \\ y(y+1) &=0 \\ y &=0 \quad \text { or } \quad y=-1 \end{aligned}\)

Volver a sustituir en\(x^{2}=y+2\) para encontrar los\(x\) -valores correspondientes.

Mesa\(\PageIndex{2}\)
Usando\(y=-1\)	Usando\(y=0\)
\ (y=-1\) ">\(\begin{aligned} x^{2} &=y+2 \\ x^{2} &=\color{Cerulean}{-1}\color{black}{+}2 \\ x^{2} &=1 \\ x &=\pm 1 \end{aligned}\)	\ (y=0\) ">\(\begin{aligned} x^{2} &=y+2 \\ x^{2} &=\color{Cerulean}{0}\color{black}{+}2 \\ x^{2} &=2 \\ x &=\pm \sqrt{2} \end{aligned}\)

Esto nos lleva a cuatro soluciones,\((±1,−1)\) y\((\pm \sqrt{2}, 0)\).

Respuesta:

\((\pm 1,-1),(\pm \sqrt{2}, 0)\)

Ejemplo\(\PageIndex{4}\)

Resolver:\(\left\{\begin{aligned}(x-1)^{2}-2 y^{2} &=4 \\ x^{2}+y^{2} &=9 \end{aligned}\right.\)

Solución

Podemos resolver para\(y^{2}\) en la segunda ecuación,

\(\left\{\begin{array}{r}{(x-1)^{2}-2 y^{2}=4} \\ {x^{2}+y^{2}=9}\end{array}\right. \Longrightarrow y^{2}=9-x^{2}\)

Sustituir\(y^{2}=9−x^{2}\) en la primera ecuación y luego resolver para\(x\).

\(\begin{aligned}(x-1)^{2}-2\color{black}{\left(\color{Cerulean}{9-x^{2}}\right) }&=4 \\ x^{2}-2 x+1-18+2 x^{2} &=0 \\ 3 x^{2}-2 x-21 &=0 \\(3 x+7)(x-3) &=0 \\ 3 x+7 &=0 \text { or } x-3=0 \\ x &=-\frac{7}{3} \quad x=3 \end{aligned}\)

Volver a sustituir en\(y^{2}=9−x^{2}\) para encontrar los\(y\) -valores correspondientes.

Mesa\(\PageIndex{3}\)
Usando\(x=-\frac{7}{3}\)	Usando\(x=3\)
\ (x=-\ frac {7} {3}\) ">\(\begin{array}{l}{y^{2}=9-\color{black}{\left(\color{Cerulean}{-\frac{7}{3}}\right)^{2}}} \\ {y^{2}=\frac{9}{1}-\frac{49}{9}} \\ {y^{2}=\frac{32}{9}} \\ {y=\pm \frac{\sqrt{32}}{3}=\pm \frac{4 \sqrt{2}}{3}}\end{array}\)	\ (x=3\) ">\(\begin{aligned} y^{2} &=9-(\color{Cerulean}{3}\color{black}{)}^{2} \\ y^{2} &=0 \\ y &=0 \end{aligned}\)

Esto lleva a tres soluciones,\(\left(-\frac{7}{3}, \pm \frac{4 \sqrt{2}}{3}\right)\) y\((3,0)\).

Respuesta:

\((3,0),\left(-\frac{7}{3}, \pm \frac{4 \sqrt{2}}{3}\right)\)

Ejemplo\(\PageIndex{5}\)

Resolver:\(\left\{\begin{aligned} x^{2}+y^{2} &=2 \\ x y &=1 \end{aligned}\right.\).

Solución

Resuelve para\(y\) en la segunda ecuación.

\(\left\{\begin{array}{r}{x^{2}+y^{2}=2} \\ {x y=1}\end{array}\right.\Longrightarrow y=\frac{1}{x}\)

Sustituir\(y=\frac{1}{x}\) en la primera ecuación y luego resolver para\(x\).

\(x^{2}+\left(\frac{1}{x}\right)^{2}=2\)
\(x^{2}+\frac{1}{x^{2}}=2\)

Esto nos deja con una ecuación racional. Toma nota de eso\(x≠0\) y multiplica ambos lados por\(x^{2}\).

\(\begin{aligned} \color{Cerulean}{x^{2}}\color{black}{\left(x^{2}+\frac{1}{x^{2}}\right)} &=2 \cdot \color{Cerulean}{x^{2}} \\ x^{4}+1 &=2 x^{2} \\ x^{4}-2 x^{2}+1 &=0 \\\left(x^{2}-1\right)\left(x^{2}-1\right) &=0 \end{aligned}\)

En este punto podemos ver que ambos factores son los mismos. Aplicar la propiedad cero del producto.

\(\begin{aligned} x^{2}-1 &=0 \\ x^{2} &=1 \\ x &=\pm 1 \end{aligned}\)

Volver a sustituir en\(y=\frac{1}{x}\) para encontrar los\(y\) -valores correspondientes.

Usando\(x=-1\)	Usando\(x=1\)
\ (x=-1\) ">\(\begin{aligned} y &=\frac{1}{x} \\ &=\frac{1}{\color{Cerulean}{-1}} \\ &=-1 \end{aligned}\)	\ (x=1\) ">\(\begin{aligned} y &=\frac{1}{x} \\ &=\frac{1}{\color{Cerulean}{1}} \\ &=1 \end{aligned}\)

Esto lleva a dos soluciones.

Respuesta:

\((1,1),(-1,-1)\)

Ejercicio\(\PageIndex{2}\)

Resolver:\(\left\{\begin{array}{r}{\frac{1}{x}+\frac{1}{y}=4} \\ {\frac{1}{x^{2}}+\frac{1}{y^{2}}=40}\end{array}\right.\)

Contestar

\(\left(-\frac{1}{2}, \frac{1}{6}\right)\left(\frac{1}{6},-\frac{1}{2}\right)\)

www.youtube.com/v/n8jj_ybegkm

Claves para llevar

Utilice el método de sustitución para resolver sistemas no lineales.
Agilice el proceso de resolución mediante el uso de expresiones algebraicas completas en el paso de sustitución para obtener una sola ecuación con una variable.
Comprender la interpretación geométrica del sistema puede ayudar a encontrar soluciones reales.

Ejercicio\(\PageIndex{3}\)

Resolver.

\(\left\{\begin{array}{c}{x^{2}+y^{2}=10} \\ {x+y=4}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}=5} \\ {x-y=-3}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=30} \\ {x-3 y=0}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}=10} \\ {2 x-y=0}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}=18} \\ {2 x-2 y=-12}\end{array}\right.\)
\(\left\{\begin{aligned}(x-4)^{2}+y^{2} &=25 \\ 4 x-3 y &=16 \end{aligned}\right.\)
\(\left\{\begin{array}{c}{3 x^{2}+2 y^{2}=21} \\ {3 x-y=0}\end{array}\right.\)
\(\left\{\begin{aligned} x^{2}+5 y^{2} &=36 \\ x-2 y &=0 \end{aligned}\right.\)
\(\left\{\begin{array}{c}{4 x^{2}+9 y^{2}=36} \\ {2 x+3 y=6}\end{array}\right.\)
\(\left\{\begin{array}{c}{4 x^{2}+y^{2}=4} \\ {2 x+y=-2}\end{array}\right.\)
\(\left\{\begin{array}{c}{2 x^{2}+y^{2}=1} \\ {x+y=1}\end{array}\right.\)
\(\left\{\begin{array}{c}{4 x^{2}+3 y^{2}=12} \\ {2 x-y=2}\end{array}\right.\)
\(\left\{\begin{aligned} x^{2}-2 y^{2} &=35 \\ x-3 y &=0 \end{aligned}\right.\)
\(\left\{\begin{array}{c}{5 x^{2}-7 y^{2}=39} \\ {2 x+4 y=0}\end{array}\right.\)
\(\left\{\begin{array}{c}{9 x^{2}-4 y^{2}=36} \\ {3 x+2 y=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {x-2 y=-12}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x^{2}+3 y=9} \\ {8 x-4 y=12}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x-4 y^{2}=3} \\ {3 x-12 y=6}\end{array}\right.\)
\(\left\{\begin{aligned} 4 x^{2}+3 y^{2} &=12 \\ x-\frac{3}{2} &=0 \end{aligned}\right.\)
\(\left\{\begin{aligned} 5 x^{2}+4 y^{2} &=40 \\ y-3 &=0 \end{aligned}\right.\)
La suma de los cuadrados de dos enteros positivos es\(10\). Si el primer entero se agrega al doble del segundo entero, la suma es\(7\). Encuentra los enteros.
La diagonal de un rectángulo mide\(\sqrt{5}\) unidades y tiene un perímetro igual a\(6\) unidades. Encuentra las dimensiones del rectángulo.
¿Para qué valores de\(b\) tendrá soluciones reales el siguiente sistema? \(\left\{\begin{array}{c}{x^{2}+y^{2}=1} \\ {y=x+b}\end{array}\right.\)
¿Para qué valores de\(m\) será el siguiente sistema tener soluciones reales? \(\left\{\begin{array}{c}{x^{2}-y^{2}=1} \\ {y=m x}\end{array}\right.\)

Contestar

1. \((1,3),(3,1)\)

3. \((-3 \sqrt{3},-\sqrt{3}),(3 \sqrt{3}, \sqrt{3})\)

5. \((-3,3)\)

7. \((-1,-3),(1,3)\)

9. \((0,2),(3,0)\)

11. \((0,1),\left(\frac{2}{3}, \frac{1}{3}\right)\)

13. \((-3 \sqrt{5},-\sqrt{5}),(3 \sqrt{5}, \sqrt{5})\)

15. \(\emptyset\)

17. \(\left(\frac{-3+3 \sqrt{5}}{2},-6+3 \sqrt{5}\right) ,\left(\frac{-3-3 \sqrt{5}}{2},-6-3 \sqrt{5}\right)\)

19. \(\left(\frac{3}{2},-1\right),\left(\frac{3}{2}, 1\right)\)

21. \(1,3\)

23. \(b \in[-\sqrt{2}, \sqrt{2}]\)

Ejercicio\(\PageIndex{4}\)

Resolver.

\(\left\{\begin{array}{c}{x^{2}+y^{2}=4} \\ {y-x^{2}=2}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {y-x^{2}=-2}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}=4} \\ {y-x^{2}=3}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}=4} \\ {4 y-x^{2}=-4}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+3 y^{2}=9} \\ {y^{2}-x=3}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+3 y^{2}=9} \\ {x+y^{2}=-4}\end{array}\right.\)
\(\left\{\begin{aligned} 4 x^{2}-3 y^{2} &=12 \\ x^{2}+y^{2} &=1 \end{aligned}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {x^{2}-y^{2}=1}\end{array}\right.\)
\(\left\{\begin{aligned} x^{2}+y^{2} &=1 \\ 4 y^{2}-x^{2}-4 y &=0 \end{aligned}\right.\)
\(\left\{\begin{aligned} x^{2}+y^{2} &=4 \\ 2 x^{2}-y^{2}+4 x &=0 \end{aligned}\right.\)
\(\left\{\begin{aligned} 2(x-2)^{2}+y^{2} &=6 \\(x-3)^{2}+y^{2} &=4 \end{aligned}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}-6 y=0} \\ {4 x^{2}+5 y^{2}+20 y=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+4 y^{2}=25} \\ {4 x^{2}+y^{2}=40}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}-2 y^{2}=-10} \\ {4 x^{2}+y^{2}=10}\end{array}\right.\)
\(\left\{\begin{array}{c}{2 x^{2}+y^{2}=14} \\ {x^{2}-(y-1)^{2}=6}\end{array}\right.\)
\(\left\{\begin{array}{c}{3 x^{2}-(y-2)^{2}=12} \\ {x^{2}+(y-2)^{2}=1}\end{array}\right.\)
La diferencia de los cuadrados de dos enteros positivos es\(12\). La suma del entero mayor y el cuadrado del menor es igual a\(8\). Encuentra los enteros.
La diferencia entre la longitud y la anchura de un rectángulo es\(4\) unidades y la diagonal mide\(8\) unidades. Encuentra las dimensiones del rectángulo. Redondear a la décima más cercana.
La diagonal de un rectángulo mide\(p\) unidades y tiene un perímetro igual a\(2q\) unidades. Encuentra las dimensiones del rectángulo en términos de\(p\) y\(q\).
El área de un rectángulo es unidades\(p\) cuadradas y su perímetro es\(2q\) unidades. Encuentra las dimensiones del rectángulo en términos de\(p\) y\(q\).

Contestar

1. \((0,2)\)

3. \(\emptyset\)

5. \((-3,0),(0,-\sqrt{3}),(0, \sqrt{3})\)

7. \(\emptyset\)

9. \((0,1),\left(-\frac{2 \sqrt{5}}{5},-\frac{1}{5}\right),\left(\frac{2 \sqrt{5}}{5},-\frac{1}{5}\right)\)

11. \((3,-2),(3,2)\)

13. \((-3,-2),(-3,2),(3,-2),(3,2)\)

15. \((-\sqrt{7}, 0),(\sqrt{7}, 0),\left(-\frac{\sqrt{55}}{3}, \frac{4}{3}\right),\left(\frac{\sqrt{55}}{3}, \frac{4}{3}\right)\)

17. \(2,4\)

19. \(\frac{q+\sqrt{2 p^{2}-q^{2}}}{2}\)unidades por\(\frac{q-\sqrt{2 p^{2}-q^{2}}}{2}\) unidades

Ejercicio\(\PageIndex{5}\)

Resolver.

\(\left\{\begin{aligned} x^{2}+y^{2} &=26 \\ x y &=5 \end{aligned}\right.\)
\(\left\{\begin{aligned} x^{2}+y^{2} &=10 \\ x y &=3 \end{aligned}\right.\)
\(\left\{\begin{aligned} 2 x^{2}-3 y^{2} &=5 \\ x y &=1 \end{aligned}\right.\)
\(\left\{\begin{array}{c}{3 x^{2}-4 y^{2}=-11} \\ {x y=1}\end{array}\right.\)
\(\left\{\begin{array}{c}{x^{2}+y^{2}=2} \\ {x y-2=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {2 x y-1=0}\end{array}\right.\)
\(\left\{\begin{aligned} 4 x-y^{2} &=0 \\ x y &=2 \end{aligned}\right.\)
\(\left\{\begin{array}{c}{3 y-x^{2}=0} \\ {x y-9=0}\end{array}\right.\)
\(\left\{\begin{aligned} 2 y-x^{2} &=0 \\ x y-1 &=0 \end{aligned}\right.\)
\(\left\{\begin{aligned} x-y^{2} &=0 \\ x y &=3 \end{aligned}\right.\)
La diagonal de un rectángulo mide\(2\sqrt{10}\) unidades. Si el área del rectángulo es unidades\(12\) cuadradas, encuentra sus dimensiones.
El área de un rectángulo es de metros\(48\) cuadrados y el perímetro mide\(32\) metros. Encuentra las dimensiones del rectángulo.
El producto de dos enteros positivos es\(72\) y su suma es\(18\). Encuentra los enteros.
La suma de los cuadrados de dos enteros positivos es\(52\) y su producto es\(24\). Encuentra los enteros.

Contestar

1. \((-5,-1),(5,1),(-1,-5),(1,5)\)

3. \(\left(-\sqrt{3},-\frac{\sqrt{3}}{3}\right),\left(\sqrt{3}, \frac{\sqrt{3}}{3}\right)\)

5. \(\emptyset\)

7. \((1,2)\)

9. \(\left(\sqrt[3]{2}, \frac{\sqrt[3]{4}}{2}\right)\)

11. \(2\)unidades por\(6\) unidades

13. \(6,12\)

Ejercicio\(\PageIndex{6}\)

Resolver.

\(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=4} \\ {\frac{1}{x}-\frac{1}{y}=2}\end{array}\right.\)
\(\left\{\begin{array}{l}{\frac{2}{x}-\frac{1}{y}=5} \\ {\frac{1}{x}+\frac{1}{y}=2}\end{array}\right.\)
\(\left\{\begin{array}{l}{\frac{1}{x}+\frac{2}{y}=1} \\ {\frac{3}{x}-\frac{1}{y}=2}\end{array}\right.\)
\(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=6} \\ {\frac{1}{x^{2}}+\frac{1}{y^{2}}=20}\end{array}\right.\)
\(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=2} \\ {\frac{1}{x^{2}}+\frac{1}{y^{2}}=34}\end{array}\right.\)
\(\left\{\begin{array}{l}{x y-16=0} \\ {2 x^{2}-y=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y^{2}=4} \\ {y=\sqrt{x}}\end{array}\right.\)
\(\left\{\begin{array}{c}{y^{2}-(x-1)^{2}=1} \\ {y=\sqrt{x}}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=2^{x}} \\ {y=2^{2 x}-56}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=3^{2 x}-72} \\ {y-3^{x}=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=e^{4 x}} \\ {y=e^{2 x}+6}\end{array}\right.\)
\(\left\{\begin{array}{l}{y-e^{2 x}=0} \\ {y-e^{x}=0}\end{array}\right.\)

Contestar

1. \(\left(\frac{1}{3}, 1\right)\)

3. \(\left(\frac{7}{5}, 7\right)\)

5. \(\left(-\frac{1}{3}, \frac{1}{5}\right),\left(\frac{1}{5},-\frac{1}{3}\right)\)

7. \((2, \sqrt{2})\)

9. \((3,8)\)

11. \(\left(\frac{\ln 3}{2}, 9\right)\)

Ejercicio\(\PageIndex{7}\)

¿Cuántas soluciones reales se pueden obtener de un sistema que consiste en un círculo y una hipérbola? Explique.
Haga su propio sistema no lineal, resuelva y proporcione la respuesta. Además, proporcionar una gráfica y discutir la interpretación geométrica de las soluciones.

Contestar: 1. La respuesta puede variar

Notas al pie

³² Un sistema de ecuaciones donde al menos una ecuación no es lineal.

Search

Text Color

Text Size

Margin Size

Font Type