2.4: Fórmulas

Última actualización
Guardar como PDF

Page ID: 111610

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Las fórmulas de la ciencia suelen contener letras variables distintas de la variable “Fórmulas” es el plural para “fórmula”. x. En efecto, las fórmulas en la ciencia suelen utilizar varias letras. Por ejemplo, la Ley Universal de Gravitación de Isaac Newton dice que la magnitud de la fuerza de atracción entre dos cuerpos celestes viene dada por la fórmula:

\[F=\frac{G M m}{r^{2}} \nonumber \]

donde$m$ generalmente denota la masa del cuerpo más pequeño,$M$ la masa del cuerpo más grande, y$r$ es la distancia entre los dos cuerpos. La letra$G$ representa la constante gravitacional universal, teniendo valor$6.67428×10^{-11}$$N(m/kg)^2$.

Caso Variable

Obsérvese el uso de la letra mayúscula y minúscula M en la Ley de Gravitación de Newton. Al trabajar con fórmulas científicas, se debe mantener el caso de las letras dadas. No se le permite sustituir minúscula por mayúscula, o mayúscula por minúscula en su trabajo.

En la Sección 2.2, describimos la meta que debe cumplirse cuando se nos pide “resolver una ecuación para”$x$.

Resolver para$x$

Cuando se le pide que resuelva una ecuación para$x$, el objetivo es manipular la ecuación en la forma final

\[x=\text {“Stuff”} \nonumber \]
donde “Stude” es una expresión matemática válida que puede contener otras variables, símbolos matemáticos, etc., pero no debe contener ninguna ocurrencia de la variable$x$.

Así, para resolver una ecuación para$x$, necesitamos aislar los términos que contienen$x$ en un lado de la ecuación, y todos los términos restantes en el otro lado de la ecuación.

Ejemplo$\PageIndex{1}$

Resolver para$x : x+a=b$.

Solución

Para deshacer los efectos de sumar a, resta a de ambos lados de la ecuación.

\[\begin{aligned} x+a &= b \quad \color{Red} \text { Original equation. } \\ x+a-a &= b-a \quad \color{Red} \text { Subtract } a \text { from both sides. } \\ x &= b-a \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Ejercicio$\PageIndex{1}$

Resolver para$x : x-c=d$.

Contestar: $x=c+d$

En Ejemplo$\PageIndex{1}$, tenga en cuenta que la respuesta$x = b−a$ tiene la forma requerida$x = \text {“Stuff”}$,, donde “Stude” es una expresión matemática válida que contiene otras variables, símbolos matemáticos, etc., pero no contiene ninguna ocurrencia de la variable$x$. Ahora bien, ¿y si nos pidieran resolver la misma ecuación para$a$, en lugar de$x$?

Ejemplo$\PageIndex{2}$

Resolver para$a : x+a=b$.

Solución

Se nos instruye para resolver la ecuación$x+a = b$ para$a$. Esto quiere decir que nuestra respuesta final debe tener la forma$a = \text {“Stuff”}$, donde “Stude” es una expresión matemática válida que contiene otras variables, símbolos matemáticos, etc., pero no contiene ninguna ocurrencia de la variable$a$. Esto significa que debemos aislar todos los términos que contienen la variable$a$ en un lado de la ecuación, y todos los términos restantes en el otro lado de la ecuación. Ahora, para deshacer el efecto de sumar$x$, restar$x$ de ambos lados de la ecuación.

\[\begin{aligned} x+a &= b \quad \color{Red} \text { Original equation. } \\ x+a-x &= b-x \quad \color{Red} \text { Subtract } x \text { from both sides. } \\ a &= b-x \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Tenga en cuenta que tenemos$a = \text {“Stuff”}$, donde “Stude” no contiene ocurrencia de$a$, la variable para la que estamos resolviendo.

Ejercicio$\PageIndex{2}$

Resolver para$x : x-c=d$.

Contestar: $c=x-d$

Ejemplo$\PageIndex{3}$

La fórmula$F = kx$, conocida como “Ley de Hooke”, predice la fuerza$F$ requerida para estirar unas$x$ unidades de resorte. Resuelve la ecuación para$k$.

Solución

Se nos instruye para resolver la ecuación$F = kx$ para$k$. Esto quiere decir que nuestra respuesta final debe tener la forma$k = \text {“Stuff”}$, donde “Stude” es una expresión matemática válida que puede contener otras variables, símbolos matemáticos, etc., pero puede que no contenga ninguna ocurrencia de la variable$k$. Esto significa que debemos aislar todos los términos que contienen la variable$k$ en un lado de la ecuación, y todos los términos restantes en el otro lado de la ecuación. Sin embargo, tenga en cuenta que todos los términos que contienen la variable ya$k$ están aislados en un lado de la ecuación. Los términos que no contienen la variable$k$ se aíslan en el otro lado de la ecuación. Ahora bien, para “deshacer” el efecto de multiplicar por$x$, dividir ambos lados de la ecuación por$x$.

\[\begin{aligned} F&= kx \quad \color{Red} \text { Original equation. } \\ \dfrac{F}{x}&= \dfrac{kx}{x} \quad \color{Red} \text { Divide both sides by } x \\ \dfrac{F}{x}&= k \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Decir eso$F/x = k$ equivale a decir eso$k = F/x$. Podemos dejar nuestra respuesta en el formulario que se muestra en el último paso, pero algunos instructores insisten en que escribamos la respuesta de la siguiente manera:

\[k=\dfrac{F}{x} \quad \color{Red} \dfrac{F}{x}=k \text { is equivalent to } k=\dfrac{F}{x} \nonumber \]

Tenga en cuenta que tenemos$k = \text {“Stuff”}$, donde “Stude” no contiene ocurrencia de$k$, la variable para la que estamos resolviendo.

Ejercicio$\PageIndex{3}$

Resolver para$m : E=m c^{2}$.

Contestar: $m=\dfrac{E}{c^{2}}$

Ejemplo$\PageIndex{4}$

La fórmula$V = RI$ se llama “Ley de Ohm”. Ayuda a calcular la caída de voltaje$V$ a través de una resistencia$R$ en un circuito eléctrico con corriente$I$. Resuelve la ecuación para$R$.

Solución

Se nos instruye para resolver la ecuación$V = RI$ para$R$. Esto quiere decir que nuestra respuesta final debe tener la forma$R = \text {“Stuff”}$, donde “Stude” es una expresión matemática válida que puede contener otras variables, símbolos matemáticos, etc., pero puede que no contenga ninguna ocurrencia de la variable$R$. Esto significa que debemos aislar todos los términos que contienen la variable$R$ en un lado de la ecuación, y todos los términos restantes en el otro lado de la ecuación. Sin embargo, tenga en cuenta que todos los términos que contienen la variable ya$R$ están aislados en un lado de la ecuación. Los términos que no contienen la variable R se aíslan en el otro lado de la ecuación. Ahora bien, para “deshacer” el efecto de multiplicar por$I$, dividir ambos lados de la ecuación por$I$.

\[\begin{aligned} V&= R I \quad \color{Red} \text { Original equation. } \\ \dfrac{V}{I}&=\dfrac{R I}{I} \quad \color{Red} \text { Divide both sides by } I \\ \dfrac{V}{I}&= R \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Esto también se puede escribir en la siguiente forma:

\[R=\dfrac{V}{I} \quad \color{Red} V / I=R \text { is equivalent to } R=V / I \nonumber \]

Tenga en cuenta que tenemos$R = \text {“Stuff”}$, donde “Stude” no contiene ocurrencia de$R$, la variable para la que estamos resolviendo.

Ejercicio$\PageIndex{4}$

Resolver para$t : d=s t$.

Contestar: $t=\dfrac{d}{s}$

Despeje de fracciones

Si las fracciones ocurren en una fórmula, limpie las fracciones de la fórmula multiplicando ambos lados de la fórmula por el denominador común.

Ejemplo$\PageIndex{5}$

La fórmula$K=\dfrac{1}{2} m v^{2}$ se utiliza para calcular la energía cinética$K$ de una partícula de masa que$m$ se mueve con velocidad$v$. Resuelve la ecuación para$m$.

Solución

Se nos pide que resolvamos la ecuación$K = (1 /2)mv^2$ para$m$. Primero, despejar las fracciones multiplicando ambos lados por el denominador común.

\[\begin{aligned} K &= \dfrac{1}{2} mv^{2} \quad \color{Red} \text { Original equation. } \\ 2(K) &= 2\left(\dfrac{1}{2} mv^{2}\right) \quad \color{Red} \text { Multiply both sides by } 2 \\ 2K &= mv^{2} \quad \color{Red} \text { Simplify. Cancel } 2^{\prime} \text { s. } \end{aligned} \nonumber \]

Tenga en cuenta que todos los términos que contienen$m$, la variable para la que estamos resolviendo, ya están aislados en un lado de la ecuación. Solo necesitamos dividir ambas partes por$v^2$ para completar la solución.

\[\begin{aligned} \dfrac{2 K}{v^2}&= \dfrac{m v^{2}}{v^{2}} \quad \color{Red} \text { Divide both sides by } v^{2} \\ \dfrac{2 K}{v^2}&= m \quad \color{Red} \text { Simplify. Cancel } v^{2} \text { for } v^{2} \end{aligned} \nonumber \]

Tenga en cuenta que la respuesta final tiene la forma$m = \text {“Stuff”}$, donde “Stude” no contiene ninguna ocurrencia de la variable$m$.

Ejercicio$\PageIndex{5}$

Resolver para$g : s=\dfrac{1}{2} g t^{2}$.

Contestar: $g=\dfrac{2 s}{t^{2}}$

Ejemplo$\PageIndex{6}$

Como se mencionó anteriormente, la Ley Universal de Gravitación de Newton se describe mediante la fórmula\[F=\dfrac{G M m}{r^{2}} \nonumber \] Resolver esta ecuación para$m$.

Solución

Se nos pide que resolvamos la ecuación$F = GMm/r^2$ para$m$. Primero, despejar las fracciones multiplicando ambos lados por el denominador común.

\[\begin{aligned} F &= \dfrac{G M m}{r^{2}} \quad \color{Red} \text { Original equation. } \\ r^{2}(F) &= r^{2}\left(\dfrac{G M m}{r^{2}}\right) \quad \color{Red} \text { Multiply both sides by } r^{2} \\ r^{2} F &= G M m \quad \color{Red} \text { Simplify. Cancel } r^{2} \text { for } r^{2} \end{aligned} \nonumber \]

\[\begin{aligned} \dfrac{r^{2} F}{G M}&= \dfrac{G M m}{G M} \quad \color{Red} \text { Divide both sides by } G M \\ \dfrac{r^{2} F}{G M}&= m \quad \color{Red} \text { Simplify. Cancel } G M \text { for } G M \end{aligned} \nonumber \]

Tenga en cuenta que la respuesta final tiene la forma$m = \text {“Stuff”}$, donde “Stude” no contiene ninguna ocurrencia de la variable$m$.

Ejercicio$\PageIndex{6}$

Resolver para$q_{2} : F=\dfrac{k q_{1} q_{2}}{r^{2}}$.

Contestar: $q_{2}=\dfrac{F r^{2}}{k q_{1}}$

Fórmulas geométricas

Veamos algunas fórmulas comúnmente utilizadas a partir de la geometría.

Ejemplo$\PageIndex{7}$

Dejar$W$ y$L$ representar el ancho y largo de un rectángulo, respectivamente, y dejar$P$ representar su perímetro.

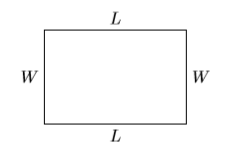
$fig 2.4.1a.png$

El perímetro (distancia alrededor) del rectángulo se encuentra sumando sus cuatro lados, luego combinando términos similares.

\[\begin{aligned} P&=L+W+L+W \quad \color{Red} \text { Summing the four sides. } \\ P&=2 W+2L \quad \color{Red} \text { Combine like terms. } \end{aligned} \nonumber \]

Resolver$P =2W +2L$ para$L$. Entonces, dado que el perímetro es$300$ pies y el ancho es$50$ pies, usa tu resultado para calcular la longitud.

Solución

Primero se nos pide que$P =2W +2L$ resolvamos$L$. Primero, aísle todos los términos que contengan la variable$L$ en un lado de la ecuación.

\[\begin{aligned} P&= 2W+2L \quad \color{Red} \text { Original equation. } \\ P-2W&= 2W+2L-2W \quad \color{Red} \text { Subtract } 2W \text { from both sides. } \\ P-2W&= 2L \quad \color{Red} \text { Simplify. } \\ \dfrac{P-2W}{2}&= \dfrac{2L}{2} \quad \color{Red} \text { Divide both sides by } 2 \\ \dfrac{P-2W}{2}&=L \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Tenga en cuenta que el resultado final tiene$L = \text {“Stuff"}$, donde “Stude” no contiene ninguna ocurrencia de la variable$L$.

La segunda parte de este ejemplo solicita que encontremos la longitud del rectángulo, dado que el perímetro es$P = 300$ pies y el ancho es$W = 50$ pies. Para calcular la longitud, sustituir$P = 300$ y$W = 50$ en$L =( P - 2W)/2$.

\[\begin{aligned} &L= \dfrac{P-2 W}{2} \quad \color{Red} \text { Perimeter formula solved for } L \\ L&= \dfrac{300-2(50)}{2} \quad \color{Red} 300 \text { for } P, 50 \text { for } W\\ L &= \dfrac{300-100}{2} \quad \color{Red} \text { Multiply: } 2(50)=100 \\ L &= \dfrac{200}{2} \quad \color{Red} \text { Subtract: } 300-100=200 \\ L &= 100 \quad \color{Red} \text { Divide: } 200 / 2=100 \end{aligned} \nonumber \]

De ahí que la longitud del rectángulo sea$100$ pies.

Ejercicio$\PageIndex{7}$

El perímetro de un rectángulo es de$160$ metros y su ancho es de$30$ metros. Encuentra su longitud.

Contestar: $L=50$metros

Ejemplo$\PageIndex{8}$

Dejar$b$ y$h$ representar la longitud de la base y la altura de un triángulo, respectivamente, y dejar$A$ representar el área del triángulo.

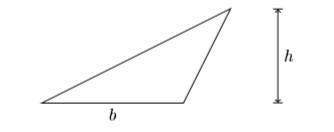
$fig 2.4.1b.png$

El área del triángulo se calcula usando la fórmula: Es$A=\dfrac{1}{2} bh$ decir, el área de un triángulo es “la mitad de la base por la altura”.

Resuelve la fórmula$A=\dfrac{1}{2} bh$ para$h$. En segundo lugar, dado que el área está$A = 90$ en ² (pulgadas$90$ cuadradas) y la longitud de la base está$15$ en ($15$pulgadas), se encuentra la altura del triángulo.

Solución

Primero se nos pide que$A = (1 /2)bh$ resolvamos$h$. Debido a que la ecuación tiene fracciones, el primer paso es borrar las fracciones multiplicando ambos lados por el mínimo denominador común.

\[\begin{aligned} A &= \dfrac{1}{2} bh \quad \color{Red} \text { Area of a triangle formula. } \\ 2(A) &= 2\left(\dfrac{1}{2} bh\right) \quad \color{Red} \text { Multiply both sides by } 2 \\ 2A &= bh \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Ahora, ya tenemos todos los términos que contienen la variable$h$ en un lado de la ecuación, por lo que podemos resolver$h$ dividiendo ambos lados de la ecuación por$b$.

\[\begin{aligned} \dfrac{2 A}{b}&= \dfrac{b h}{b} \quad \color{Red} \text { Divide both sides by } b \\ \dfrac{2 A}{b}&= h \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Tenga en cuenta que el resultado final tiene$h = \text {“Stuff"}$, donde “Stude” no contiene ninguna ocurrencia de la variable$h$.

La segunda parte de este ejemplo solicita que encontremos la altura del triángulo, dado que el área está$A = 90$ en$2$ y la longitud de la base está$b = 15$ en. Para calcular la altura del triángulo, sustituto$A = 90$ y$b = 15$ en$h =2A/b$.

\[\begin{aligned} h &= \dfrac{2 A}{b} \quad \color{Red} \text { Area formula solved for } h \\ h &= \dfrac{2(90)}{15} \quad \color{Red} \text {Substitue }90 \text { for } A, 15 \text { for } b\\ h &=\dfrac{180}{15} \quad \color{Red} \text { Multiply: } 2(90)=180 \\ h &= 12 \quad \color{Red} \text {Divide: } 180 / 15=12 \end{aligned} \nonumber \]

De ahí que la altura del triángulo sea$12$ pulgadas.

Ejercicio$\PageIndex{8}$

El área de un triángulo es$140$ cm ² y la longitud de su base es$70$ cm. Encuentra la altura del triángulo.

Contestar: $4$cm