2.5: Aplicaciones

Última actualización
Guardar como PDF

Page ID: 111599

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

La solución de un problema verbal debe incorporar cada uno de los siguientes pasos.

Requisitos para soluciones de problemas de Word

Configura un Diccionario de Variables. Debes dejar saber a tus lectores qué representa cada variable en tu problema. Esto se puede lograr de varias maneras:
- Declaraciones como “Vamos a$P$ representar el perímetro del rectángulo”.
- Etiquetar valores desconocidos con variables en una tabla.
- Etiquetar cantidades desconocidas en un boceto o diagrama.
Configura una ecuación.Cada solución a un problema de palabras debe incluir una ecuación cuidadosamente elaborada que describa con precisión las restricciones en la declaración del problema.
Resuelve la Ecuación. Siempre debes resolver la ecuación establecida en el paso anterior.
Responda a la Pregunta. Este paso se pasa por alto fácilmente. Por ejemplo, el problema podría preguntar por la edad de Jane, pero la solución de tu ecuación da la edad de la hermana de Jane, Liz. Asegúrate de responder la pregunta original hecha en el problema. Su solución debe escribirse en una oración con las unidades correspondientes.
Mira hacia atrás. Es importante señalar que este paso no implica que simplemente deba verificar su solución en su ecuación. Después de todo, es posible que tu ecuación modele incorrectamente la situación del problema, por lo que podrías tener una solución válida a una ecuación incorrecta. La pregunta importante es: “¿Tiene sentido tu respuesta con base en las palabras de la declaración original del problema?”

Demos una prueba de manejo a estos requisitos.

Ejemplo$\PageIndex{1}$

Tres veces más de cinco veces un cierto número es$-62$. Encuentra el número.

Solución

En la solución, abordamos cada paso de los Requisitos para Soluciones de Problemas de Word.

Configura un Diccionario de Variables. Vamos a$x$ representar el número desconocido.
Configura una Ecuación. “Tres veces más de cinco veces un cierto número es$-62$” se convierte en:

$fig 2.5.1a.png$

Resuelve la Ecuación. Para resolver$x$, primero restar$3$ de ambos lados de la ecuación. \[\begin{aligned} 3+5 x &= -62 \quad \color {Red} \text { Original equation. } \\ 3+5 x-3 &= -62-3 \quad \color {Red} \text { Subtract } 3 \text { from both sides. } \\ 5x &= -65 \quad \color {Red} \text { Simplify. } \\ \dfrac{5 x}{5} &= \dfrac{-65}{5} \quad \color {Red} \text { Divide both sides by } 5 \\ x &= -13 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Responda a la Pregunta. El número desconocido es$-13$.
Mira hacia atrás. Calcular “tres veces más de cinco veces”$-13$. \[\begin{aligned} 3+5(-13) &=3+(-65) \\ &=-62 \end{aligned} \nonumber \]De ahí que tres veces más de cinco veces$-13$ sea$-62$, según se requiera. Nuestra solución es correcta.

Ejercicio$\PageIndex{1}$

$27$ more than $5$ times a certain number is $-148$. What is the number?

Responder: $-35$

Ejemplo$\PageIndex{2}$

La suma de tres enteros consecutivos es$-66$. Encuentra el más pequeño de estos tres enteros.

Solución

En la solución, abordamos cada paso de los Requisitos para Soluciones de Problemas de Word.

Configura un Diccionario de Variables. Let$k$ representa el menor de tres enteros consecutivos.
Configura una Ecuación. Un ejemplo de tres enteros consecutivos es$34$,$35$, y$36$. Estos no son los enteros que buscamos, sino que sirven para ayudar en la comprensión del problema. Observe cómo cada entero consecutivo es uno más grande que el entero anterior. Si$k$ es el menor de tres enteros consecutivos, entonces los siguientes dos enteros consecutivos son$k +1$ y$k +2$. La “suma de tres enteros consecutivos es$-66$” se convierte en:

$fig 2.5.1b.png$

Resuelve la Ecuación. Para resolver$k$, primero simplifique el lado izquierdo de la ecuación combinando términos similares. \[\begin{aligned} k+(k+1)+(k+2) &=-66 \quad \color {Red} \text { Original equation. }\\ 3k+3 &=-66 \quad \color {Red} \text { Combine like terms. }\\ 3k+3-3 &=-66-3 \quad \color {Red} \text { Subtract } 3 \text { from both sides.}\\ 3k &=-69 \quad \color {Red} \text { Simplify. }\\ \dfrac{3k}{3} &=\dfrac{-69}{3} \quad \color {Red} \text { Divide both sides by } 3.\\ k &=-23 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Responda a la Pregunta. El más pequeño de tres enteros consecutivos es$-23$.
Mira hacia atrás. Si$k = -23$ es el menor de tres enteros consecutivos, entonces los siguientes dos enteros consecutivos son$-22$ y$-21$. Comprobemos la suma de estos tres enteros consecutivos. \[-23+(-22)+(-21)=-66 \nonumber \]De ahí que la suma de los tres enteros consecutivos sea$-66$, según se requiera. Nuestra solución es correcta

Ejercicio$\PageIndex{2}$

La suma de tres enteros impares consecutivos es$-225$. What are the integers?

Responder: $-77,-75,-73$

Ejemplo$\PageIndex{3}$

Un carpintero corta una tabla que mide$60$ pulgadas en tres piezas. La segunda pieza es el doble de larga que la primera pieza, y la tercera es tres veces más larga que la primera pieza. Encuentra la longitud de cada pieza cortada por el carpintero.

Solución

En la solución, abordamos cada paso de los Requisitos para Soluciones de Problemas de Word.

Configura un Diccionario de Variables. Dejar$L$ representar la longitud de la primera pieza. Entonces la segunda pieza, que es el doble de larga que la primera pieza, tiene longitud$2L$. La tercera pieza, que es tres veces más larga que la primera pieza, tiene longitud$3L$. Construyamos una mesita para ayudar a resumir la información proporcionada en este problema.

Pieza	Largo (pulg)
Primera pieza	L
Segunda pieza	2L
Tercera pieza	3L
Longitud total	60

Configura una Ecuación. Como puede ver en la tabla anterior, la segunda columna muestra que la suma de las tres piezas es$60$ pulgadas. En símbolos:\[L+2 L+3 L=60 \nonumber \]
Resuelve la Ecuación. Para resolver$L$, primero simplifique el lado izquierdo de la ecuación combinando términos similares. \[\begin{aligned} L+2 L+3 L &= 60 \quad \color {Red} \text { Original equation. } \\ 6L &= 60 \quad \color {Red} \text { Combine like terms. } \\ \dfrac{6L}{6} &= \dfrac{60}{6} \quad \color {Red} \text { Divide both sides by } 6 \\ L &= 10 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Responda a la Pregunta. La primera pieza tiene longitud L = 10 pulgadas. La segunda pieza tiene longitud 2L = 20 pulgadas. La tercera pieza tiene longitud 3L = 30 pulgadas. En forma tabular, esto es aún más evidente.

Pieza	Largo (pulg)	Largo (pulg)
Primera pieza	L	10
Segunda pieza	2L	20
Tercera pieza	3L	30
Longitud total	60	60

Mira hacia atrás. No solo la segunda longitud es el doble de la primera y la tercera longitud tres veces la primera, verifica la suma de sus longitudes:\[10+20+30=60 \nonumber \] Eso es un total de$60$ pulgadas. Tenemos la solución correcta.

Ejercicio$\PageIndex{3}$

Han corta una tabla que$230$ inches in three pieces. The second piece is twice as long as the mide la primera pieza, y la tercera pieza es$30$ inches longer than the second piece. Find the length of each piece cut by Han.

Responder: $40,80,110$en

Ejemplo$\PageIndex{4}$

Los tres lados de un triángulo son enteros pares consecutivos. Si el perímetro (suma de los tres lados) del triángulo es$156$ centímetros, busque la longitud de cada lado del triángulo.

Solución

En la solución, abordamos cada paso de los Requisitos para Soluciones de Problemas de Word.

Configura un Diccionario de Variables. Un ejemplo de tres enteros pares consecutivos es$18$,$20$, y$22$. Estos no son los enteros que buscamos, pero sí nos dan algún sentido del significado de tres enteros pares consecutivos. Tenga en cuenta que cada entero par consecutivo es dos más grande que el entero anterior. Así, si$k$ es la longitud del primer lado del triángulo, entonces los dos lados siguientes son$k+2$ y$k+4$. En este ejemplo, nuestro diccionario de variables tomará la forma de una ﬁgura bien etiquetada.

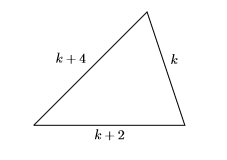
$fig 2.5.1c.png$

Configura una Ecuación. El perímetro del triángulo es la suma de los tres lados. Si el perímetro es de$156$ centímetros, entonces:\[k+(k+2)+(k+4)=156 \nonumber \]
Resuelve la Ecuación. Para resolver para k, primero simplifique el lado izquierdo de la ecuación combinando términos similares. \[\begin{aligned} k+(k+2)+(k+4) &=156 \quad \color {Red} \text { Original equation. }\\ 3k+6 &=156 \quad \color {Red} \text { Combine like terms. }\\ 3k+6-6 &=156-6 \quad \color {Red} \text { Subtract } 6 \text { from both sides.}\\ 3k &=150 \quad \color {Red} \text { Simplify. }\\ \dfrac{3k}{3} &=\dfrac{150}{3} \quad \color {Red} \text { Divide both sides by } 3.\\ k &=50 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Responda a la Pregunta. Así, el primer lado tiene$50$ centímetros de longitud. Porque los siguientes dos enteros pares consecutivos son$k+2=52$ y$k+4= 54$, los tres lados del triángulo miden$50$,$52$, y$54$ centímetros, respectivamente.
Mira hacia atrás. Una imagen ayuda a nuestra comprensión. Los tres lados son enteros pares consecutivos.

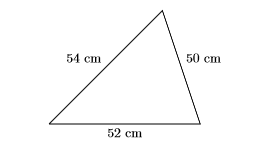
$fig 2.5.1d.png$

Obsérvese que el perímetro (suma de los tres lados) es:\[50 \mathrm{cm}+52 \mathrm{cm}+54 \mathrm{cm}=156 \mathrm{cm} \nonumber \] Así, el perímetro es$156$ centímetros, como debería ser. Nuestra solución es correcta.

Ejercicio$\PageIndex{4}$

Los tres lados de un triángulo son números enteros consecutivos. Si el perímetro (suma de los tres lados) del triángulo$453$ centimeters, se encuentra la longitud de cada lado del triángulo.

Responder: $150,151,152 $cm

Ejemplo$\PageIndex{5}$

Un hecho bien conocido de la geometría es el hecho de que la suma de los ángulos de un triángulo es$180^{\circ}$. Supongamos que tenemos un triángulo cuyo segundo ángulo es$10$ grados mayor que el doble de su primer ángulo y cuyo tercer ángulo es$50$ grados mayor que su primer ángulo. Encuentra la medida de cada ángulo del triángulo.

Solución

En la solución, abordamos cada paso de los Requisitos para Soluciones de Problemas de Word.

Configura un Diccionario de Variables. El alfabeto griego comienza con las letras$\alpha, \beta, \gamma, \delta, \epsilon, \ldots,$ de la misma manera que el alfabeto inglés comienza con las letras A los$a, b, c, d, e, \ldots$ matemáticos les encanta usar letras griegas, especialmente en el estudio de la trigonometría. La letra griega$\theta$ (pronunciada “theta”) es particularmente favorecida al representar un ángulo de un triángulo. Entonces, dejaremos$\theta$ representar la medida de grado del primer ángulo del triángulo. El segundo ángulo es$10$ grados mayor que el doble del primer ángulo, por lo que el segundo ángulo es$2\theta+10$. El tercer ángulo es$50$ grados mayor que el primer ángulo, por lo que el tercer ángulo es$\theta+50$. Nuevamente, configuraremos una ﬁgure bien etiquetada para nuestro diccionario de variables.

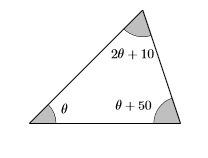
$fig 2.5.1e.png$

Configura una Ecuación. La suma de los ángulos es$180^{\circ}$, entonces:\[\theta+(2 \theta+10)+(\theta+50)=180 \nonumber \]
Resuelve la Ecuación. Para resolver$\theta$, primero simplifique el lado izquierdo de la ecuación combinando términos similares. \[\begin{aligned} \theta+(2 \theta+10)+(\theta+50) & =180 \quad \color {Red} \text { Original equation. }\\ 4 \theta+60 & =180 \quad \color {Red} \text { Combine like terms. }\\ 4 \theta+60-60 & =180-60 \quad \color {Red} \text { Subtract } 60 \text { from both sides.}\\ 4 \theta & =120 \quad \color {Red} \text { Simplify. }\\ \dfrac{4 \theta}{4} & =\dfrac{120}{4} \quad \color {Red} \text { Divide both sides by } 4.\\ \theta & =30 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Responda a la Pregunta. Así, el primer ángulo son$\theta=30$ grados, el segundo ángulo son$2\theta+10=70$ grados y el tercer ángulo son$\theta+50=80$ grados.
Mira hacia atrás. Una imagen ayuda a nuestra comprensión. Tenga en cuenta que el segundo ángulo es 10 grados mayor que el doble del primer ángulo. Tenga en cuenta que el tercer ángulo es$50$ grados mayor que el primer ángulo.

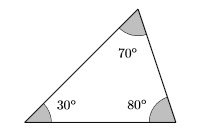
$fig 2.5.1f.png$

Obsérvese que la suma de los ángulos es:\[30^{\circ}+70^{\circ}+80^{\circ}=180^{\circ} \nonumber \] Así, la suma de los tres ángulos es de 180 grados, como debería ser. Tenemos la solución correcta.

Ejercicio$\PageIndex{5}$

El segundo ángulo de un triángulo es tres veces mayor que el primer ángulo. El tercer ángulo del triángulo es un$40$ degrees larger than the second angle. How many degrees are in each angle?

Responder: $20^{\circ}, 60^{\circ}, 100^{\circ}$

Ejemplo$\PageIndex{6}$

Martha hereda$\$21,000$ y decide invertir el dinero en tres cuentas separadas. El monto que invierte en la segunda cuenta es el doble de lo que invierte en la primera cuenta. El monto que invierte en la tercera cuenta es$\$1,000$ mayor que el monto que invierte en la segunda cuenta. ¿Cuánto invirtió en cada cuenta?

Solución

En la solución, abordamos cada paso de los Requisitos para Soluciones de Problemas de Word.

Configura un Diccionario de Variables. Usaremos una tabla en este ejemplo para ayudar a configurar nuestro diccionario de variables. $x$Sea la cantidad invertida en la primera cuenta. El monto invertido en la segunda cuenta es el doble de lo invertido en la primera cuenta, así$2x$ es el monto invertido en la segunda cuenta. La inversión en tercera cuenta es$\$1,000$ mayor que la cantidad invertida en la segunda cuenta, por lo que es$2x + 1000$.

Cuenta #	Monto invertido
Cuenta #1	x
Cuenta #2	2x
Cuenta #3	2x+1000
Total Invertido	21000

Configura una Ecuación. La segunda columna de la tabla revela la ecuación requerida. Las tres inversiones deben sumar a$\$21,000$. \[x+2 x+(2 x+1000)=21000 \nonumber \]
Resuelve la Ecuación. Para resolver$x$, primero simplifique el lado izquierdo de la ecuación combinando términos similares. \[\begin{aligned} x+2 x+(2 x+1000) &=21000 \quad \color {Red} \text { Original equation. }\\ 5 x+1000 &=21000 \quad \color {Red} \text { Combine like terms. }\\ 5 x+1000-1000 &=21000-1000 \quad \color {Red} \text { Subtract } 1000 \text { from both sides.}\\ 5 x &=20000 \quad \color {Red} \text { Simplify. }\\ \dfrac{5 x}{5} &=\dfrac{20000}{5} \quad \color {Red} \text { Divide both sides by } 5.\\ x &=4000 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Responda a la Pregunta. Sustituir$x = 4000$ en cada entrada de la segunda columna de la tabla anterior para producir los resultados en la siguiente tabla.

Cuenta #	Monto invertido	Monto invertido
Cuenta #1	x	$4,000
Cuenta #2	2x	$8,000
Cuenta #3	2x+1000	$9,000
Total Invertido	21000	21,000

Mira hacia atrás. Como podemos ver en nuestra tabla de respuestas, el monto$\$8,000$ invertido en la segunda cuenta es el doble del monto invertido en la primera cuenta. El monto$\$9,000$ invertido en la tercera cuenta es$\$1,000$ mayor que el monto invertido en la segunda cuenta. Además, la inversión total es:\[\$ 4,000+\$ 8,000+\$ 9,000=\$ 21,000 \nonumber \] Así, la inversión total es$\$21,000$, como debería ser. Tenemos la solución correcta.

Ejercicio$\PageIndex{6}$

Jim hereda$\$15,000$. He invests part in a fund that pays $5\%$ per year and the rest in a fund that pays $4\%$ per year. At the end of one year, the combined interest from both investments was $\$4,250$. How much did he invest in each fund?

Responder: $\$ 5,000$en$5\%$ y$\$ 10,000$ en$4\% $.

Ejemplo$\PageIndex{7}$

Jeestá haciendo senderismo por la$2,650$ milla Paciﬁc Crest Trail de México a Canadá. Poco antes de cruzar de Oregón a Washington se encuentra cuatro veces más lejos del inicio del sendero que desde el final. ¿Cuánto más tiene que caminar?

Solución

En la solución, abordamos cada paso de los Requisitos para Soluciones de Problemas de Word.

Configura un Diccionario de Variables. Dejar$d$ representar la distancia que queda para que Je, camine. Debido a que Jede se encuentra cuatro veces más lejos del inicio del sendero que del final, la distancia Jede ya completada es$4d$. Construyamos una mesita para ayudar a resumir la información proporcionada en este problema.

Sección de Sendero	Distancia (mi)
Distancia hasta el fin	d
Distancia desde el inicio	4d
Distancia total	2650

Configura una Ecuación. Como puede ver en la tabla anterior, la segunda columna muestra que la suma de las dos distancias es$2650$ millas. En símbolos:\ [d+4 d=2650\ nonumber\
Resuelve la Ecuación. Para resolver$d$, primero simplifique el lado izquierdo de la ecuación combinando términos similares. \[\begin{aligned} d+4d & =2650 \quad \color {Red} \text { Original equation. } \\ 5d & =2650 \quad \color {Red} \text { Combine like terms. } \\ \dfrac{5d}{5} & =\dfrac{2650}{5} \quad \color {Red} \text { Divide both sides by } 5 \\ d & =530 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Responda a la Pregunta. Je, todavía le quedan$530$ kilómetros por recorrer.
Mira hacia atrás. Debido a que la cantidad que queda para caminar es$d = 530$ millas, la distancia de Jede desde el inicio del sendero es$4d = 4(530)$, o$2,120$ millas. Si organizamos estos resultados en forma tabular, es evidente que no sólo la distancia desde el inicio del sendero es cuatro veces mayor que la distancia que queda hasta el final, sino que la suma de sus longitudes es igual a la longitud total del sendero.

Sección de Sendero	Distancia (mi)	Distancia (mi)
Distancia hasta el fin	d	530
Distancia desde el inicio	4d	2120
Distancia total	2650	2650

Así, tenemos la solución correcta.

Ejercicio$\PageIndex{7}$

Margaret va en bicicleta por un carril que mide$100$ miles. If Magaret está cuatro veces más lejos del inicio del viaje que del final, ¿cuántas millas más tiene que recorrer antes de finalizar su paseo?

Responder: $20$millas

Ejemplo$\PageIndex{8}$

Hoy$15\%$ de la clase de séptimo grado de la hermana Damaris estaban enfermos y se quedaron en casa de la escuela. Si solo hay$34$ estudiantes presentes, ¿cuál es el tamaño real de la clase de la hermana Damaris'?

Solución

En la solución, abordamos cada paso de los Requisitos para Soluciones de Problemas de Word.

Configura un Diccionario de Variables. Vamos a$S$ representar el tamaño real de la clase de la hermana Damaris'.
Configura una Ecuación. Si$15\%$ de la clase de la hermana Damaris' estaba ausente, entonces$85\%$ de su clase estaba presente. Hay$34$ estudiante presente, por lo que la frase “$85\%$de la clase de la hermana Damaris' es$34$” se traduce en la ecuación,\[0.85 S=34 \nonumber \] donde hemos cambiado$85\%$ a un decimal moviendo el punto decimal dos lugares hacia la izquierda.
Resuelve la Ecuación. Para resolver para$S$, primero borra los decimales multiplicando ambos lados de la ecuación por$100$. \[\begin{aligned} 0.85S &= 34 \quad \color {Red} \text { Original equation. } \\ 85S &= 3400 \quad \color {Red} \text { Multiply both sides by } 100. \\ \dfrac{85S}{85}&= \dfrac{3400}{85} \quad \color {Red} \text { Divide both sides by } 85 \\ S&= 40 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Responda a la Pregunta. El tamaño de la clase de la hermana Damaris es$40$.
Mira hacia atrás. Nos dicen que$15\%$ de la clase de la hermana Damari está ausente. Si calculamos$15\%$ de$40$, obtenemos:\[0.15(40)=6 \nonumber \] Así, hubo 6 estudiantes ausentes, entonces$40-6$, o$34$ estudiantes estuvieron presentes. Así, tenemos la solución correcta.

Ejercicio$\PageIndex{8}$

$20\%$de la clase de Mary estaban enfermos y se quedaron en casa de la escuela. Si tan solo$36$ students are present, what is the actual size of Mary’s class?

Responder: $45$

Search

Text Color

Text Size

Margin Size

Font Type