5.1: Funciones

Última actualización
Guardar como PDF

Page ID: 111671

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Comenzamos con la definición de una relación.

Relación

Una relación es una colección de pares ordenados.

La colección de pares ordenados\[R =\{(0,3),(0,4),(1,5),(2,6)\} \nonumber \] es un ejemplo de una relación.

Si recogemos el primer elemento de cada par ordenado en un conjunto, tenemos lo que se llama el dominio de la relación.

Dominio

El dominio de una relación es el conjunto de todos los primeros elementos de los pares ordenados.

Por ejemplo, en la relación\[R = \{(0,3),(0,4),(1,5),(2,6)\} \nonumber \] si recogemos el primer elemento de cada par ordenado en$R$, obtenemos el dominio:\[\text {Domain of R} = \{0,1,2\} \nonumber \] Aunque el número cero aparece dos veces como primer elemento en los pares ordenados de$R$, tenga en cuenta que lo enumeramos solo una vez al enumerar los elementos en el dominio de $R$.

De manera similar, si recolectamos los segundos elementos de cada par ordenado en un conjunto, tenemos lo que se llama el rango de una relación.

Rango

El rango de una relación es el conjunto de todos los segundos elementos de los pares ordenados.

Por ejemplo, en la relación\[R = \{(0,3),(0,4),(1,5),(2,6)\} \nonumber \] si recogemos el segundo elemento de cada par ordenado en$R$, obtenemos el rango:\[\text {Range of R} = \{3,4,5,6\} \nonumber \]

Ejemplo$\PageIndex{1}$

Indicar el dominio y el alcance de la relación\[T = \{(5,3),(6,3),(7,4)\} \nonumber \]

Solución

Recoge el primer elemento de cada par ordenado$T$ para listar el dominio:

Dominio de$T=\{5,6,7\}$

Recoge el segundo elemento de cada par ordenado$T$ para enumerar el rango:

Rango de$T=\{3,4\}$

Tenga en cuenta que aunque el número tres aparezca dos veces en la segunda posición, lo enumeramos solo una vez al describir el rango.

Ejercicio$\PageIndex{1}$

Indicar el dominio y el alcance de la relación\[S =\{(−1,7),(2,5),(2,3)\} \nonumber \]

Contestar: Dominio de$S = \{−1,2\}$, Range of $S = \{3,5,7\}$

Ejemplo$\PageIndex{2}$

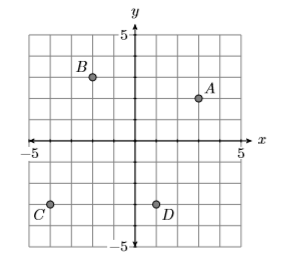
Indicar el dominio y el rango de la relación que se muestra en la Figura$\PageIndex{1}$.

higo 5.1.1.png — Figura$\PageIndex{1}$: Podemos presentar una relación como una colección de pares ordenados en una gráfica.

Solución

$A$El punto tiene coordenadas$(3,2)$, el punto$B$ tiene coordenadas$(−2,3)$, el punto$C$ tiene coordenadas$(−4,−3)$ y el punto$D$ tiene coordenadas$(1,−3)$. Podemos recoger estos puntos en un conjunto. \[S = \{(3,2),(−2,3),(−4,−3),(1,−3)\} \nonumber \]

Si recogemos cada elemento en la primera posición de cada par ordenado, tenemos el dominio.

Dominio de$S = \{−4,−2,1,3\}$

Tenga en cuenta que es tradicional listar los elementos del dominio en orden (de menor a mayor). A continuación, si recogemos cada elemento en la segunda posición de cada par ordenado, tenemos el rango.

Rango de$S = \{−3,2,3\}$

Nuevamente, es tradicional enumerar los elementos en orden. Obsérvese nuevamente que no repetimos$−3$ el número al enumerar el rango, a pesar de que se usa dos veces como segundo elemento de un par ordenado en el conjunto$S$.

Ejercicio$\PageIndex{2}$

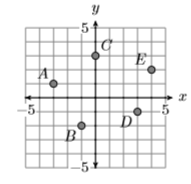
Indicar el dominio y el rango de la relación que se muestra a continuación.

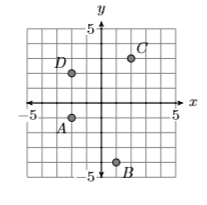
$Ex 5.1.2.png$

Contestar: Dominio de$S =\{−2,1,2\}$, Range of $S =\{−4,−1,2,3\}$

Diagramas de mapeo

Un diagrama de mapeo es una construcción útil que ayuda a analizar una relación. Consideremos la relación anterior$R =\{(0,3),(0,4),(1,5),(2,6)\}$, que tenía dominio$\mathcal{D} = \{0,1,2\}$ y rango$\mathcal{R} = \{3,4,5,6\}$. Para construir un diagrama de mapeo para$R$, enumere los elementos en el dominio de$R$ a la izquierda, enumere los elementos del rango de$R$ a la derecha, luego use flechas para indicar los pares ordenados (ver Figura$\PageIndex{2}$).

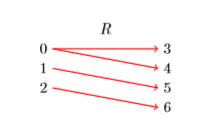
higo 5.1.2.png — Figura$\PageIndex{2}$: Uso de un diagrama de mapeo para describir la relación$R$.

Observe cómo$(0,3)$ se indica el par ordenado dibujando una flecha que conecta$0$ de la izquierda a$3$ la derecha. Decimos que la relación “mapea$0$$3$” y escribe$R : 0 \rightarrow 3$. De manera similar:

El par ordenado$(0,4)$ se indica dibujando una flecha que conecta$0$ de la izquierda a$4$ la derecha; es decir,$R$ “mapas$0$ a$4$” o$R :0→ 4$.
El par ordenado$(1,5)$ se indica dibujando una flecha que conecta$1$ de la izquierda a$5$ la derecha; es decir,$R$ “mapas$1$ a$5$” o$R :1→ 5$.
El par ordenado$(2,6)$ se indica dibujando una flecha que conecta$2$ de la izquierda a$6$ la derecha; es decir,$R$ “mapas$2$ a$6$” o$R :2→ 6$.

Ejemplo$\PageIndex{3}$

Crear un diagrama de mapeo para la relación en Ejemplo$\PageIndex{1}$.

Solución

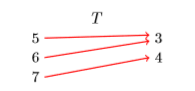
La relación de Ejemplo$\PageIndex{1}$ es$T=\{(5,3),(6,3),(7,4)\}$. Enumere$\mathcal{D}=\{5,6,7\}$ el dominio a la izquierda,$\mathcal{R}=\{3,4\}$ el rango a la derecha, luego use flechas para indicar los pares ordenados (ver Figura$\PageIndex{3}$).

higo 5.1.3.png — Figura$\PageIndex{3}$: Diagrama de mapeo para la relación$T$.

Deﬁnición de la función

Una función es un tipo de relación muy especial.

Función

Una relación es una función si y solo si cada objeto en el dominio está emparejado con exactamente un objeto en el rango.

Como primer ejemplo, considere la relación$R = \{(0,3),(0,4),(1,5),(2,6)\}$ cuyo diagrama de mapeo se representa en la Figura$\PageIndex{2}$. Tenga en cuenta que$0$ en el dominio se empareja con dos objetos,$3$ y$4$, en el rango. De ahí que la relación$R$ sea no es una función.

Como segundo ejemplo, considere la relación$T =\{(5,3),(6,3),(7,4)\}$, cuyo diagrama de mapeo se representa en la Figura$\PageIndex{3}$. En este ejemplo, cada objeto de dominio se empareja con exactamente un objeto range:$5$ solo se envía a$3$,$6$ solo se envía a$3$, y$7$ solo se envía a$4$. De ahí que la relación$T$ sea una función. El hecho de que el objeto range$3$ se use dos veces no importa. Es el hecho de que cada objeto de dominio se envía a exactamente un objeto de rango lo que importa.

Ejemplo$\PageIndex{4}$

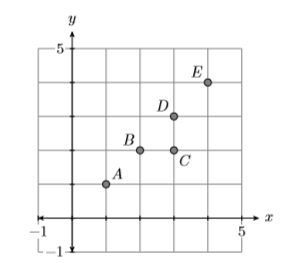
Considera la relación que se muestra en la Figura$\PageIndex{4}$. ¿Es una función?

higo 5.1.4.png — Figura$\PageIndex{4}$: ¿Es esta relación una función?

Solución

La gráfica de la Figura$\PageIndex{4}$ consiste en los puntos$A(1,1)$$B(2,2)$,$C(3,2)$,$D(3,3)$, y$E(4,4)$. El dominio es$\mathcal{D}=\{1,2,3,4\}$ y el rango es$\mathcal{R}=\{1,2,3,4\}$. Un diagrama de mapeo (ver Figura$\PageIndex{5}$) nos ayudará a decidir si la relación representada por la gráfica es una función. Pon el dominio a la izquierda, el rango a la derecha, luego usa flechas para indicar los pares ordenados. Llamemos a la relación$f$.

Ex 5.1.4.png — Figura$\PageIndex{5}$: Diagrama de mapeo para la relación$f$ representada en la Figura$\PageIndex{4}$.

En la Figura$\PageIndex{5}$, observe cómo el objeto de dominio$3$ se “envía a” o se empareja con dos objetos de rango,$2$ y$3$. De ahí que la relación no$f$ sea una función.

Ejercicio$\PageIndex{4}$

Considera la relación que se muestra a continuación. ¿Es una función?

$Ex 5.1.4.png$

Contestar: Sí, la relación es una función.

Ejemplo$\PageIndex{5}$

La siguiente relación empareja automóviles con su kilometraje de gasolina. Determinar si la relación es una función.

\[T =\{\text {(Bentley Mulsanne,18),(Kia Soul,30),(Lamborghini Gallardo,20), (Smart Fortwo,41),(Jaguar XF,23)} \} \nonumber \]

Solución

En la Figura$\PageIndex{6}$, creamos un diagrama de mapeo que indica la relación entre los automóviles y su kilometraje de gasolina. Tenga en cuenta que cada objeto de dominio de la izquierda está emparejado con exactamente un objeto de rango a la derecha. De ahí que esta relación sea una función.

higo 5.1.6.png — Figura$\PageIndex{6}$: Diagrama de mapeo para la relación$T$.

Ejercicio$\PageIndex{5}$

La siguiente relación empareja a las personas con su edad. Determinar si la relación es una función.

\[S = \{\text {(Mary,23),(Joe,18), (Alfonzo,20),(Zoe,18), (Maria,22),(Chris,23) } \} \nonumber \]

Contestar: Sí, la relación es una función.

Ejemplo$\PageIndex{6}$

La siguiente relación empareja a un ave en particular con el estado que ha adoptado a esa ave como su ave estatal. Determinar si la relación es una función.

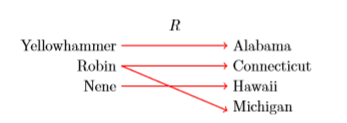
\[R=\{\text { (Yellowhammer, Alabama), (Robin, Connecticut), (Nene, Hawaii), (Robin, Michigan) } \} \nonumber \]

Solución

En Figura$\PageIndex{7}$, creamos un diagrama de mapeo que indica la relación entre las aves y sus adopciones estatales. Tenga en cuenta que el objeto de dominio “Robin” está emparejado con dos objetos de rango, “Connecticut” y “Michigan”, de ahí que esta relación no sea una función.

higo 5.1.7.png — Figura$\PageIndex{7}$: Diagrama de mapeo para la relación$R$.

Ejercicio$\PageIndex{6}$

La siguiente relación empareja a las personas con los tipos de autos que poseen. Determinar si la relación es una función.

\[S = \{\text {(Bernard,station wagon), (Tina,truck), (Gilberto,sedan), (Kate,sport utility), (Bernard,sedan), (Kate,minivan)} \} \nonumber \]

Contestar: No, la relación no es una función.

Notación de diagrama de mapeo

El objetivo de esta sección es introducir la notación de funciones. Comencemos con el diagrama de mapeo en la Figura$\PageIndex{8}$.

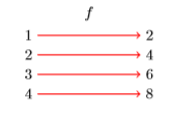
higo 5.1.8.png — Figura$\PageIndex{8}$: Diagrama de mapeo.

El diagrama de mapeo en la Figura$\PageIndex{8}$ revela los siguientes hechos:

$f$mapas$1$ a$2$ o$f :1→ 2$
$f$mapas$2$ a$4$ o$f :2→ 4$
$f$mapas$3$ a$6$ o$f :3→ 6$
$f$mapas$4$ a$8$ o$f :4→ 8$

Observe cómo la notación$f :4→ 8$ se correlaciona muy bien con el diagrama de mapeo en la Figura$\PageIndex{8}$. La notación$f :4→ 8$ se lee “$f$mapas$4$ a$8$” o “$f$envía$4$ a”$8$.

Una mirada más cercana al diagrama de mapeo en la Figura$\PageIndex{8}$ revela un patrón interesante. La “regla” parece ser que la relación$f$ duplica cada entrada en su dominio: dos veces$1$ es$2$, dos$2$ veces$3$ es$6$, dos veces es, etc. Es posible dar una descripción general de esta “regla” escribiendo: Es\[f : x→ 2x (5.1) \label{Eq5.1.1} \] decir,$f$ envía$4$ $x$a dos veces$x$, o equivalentemente,$2x$. Por ejemplo, podríamos preguntar “¿a dónde$f$ envía$15$?” Para responder a esta pregunta, la$x$ sustituiríamos por$15$ en la regla\ ref {Eq5.1.1} para obtener\[f : 15→ 2(15) \nonumber \] o equivalentemente, También\[f : 15→ 30 \nonumber \] podríamos preguntar “¿a dónde$f$ envía$−7$?” Para responder a esta pregunta, reemplazaríamos$x$ con$−7$ en la regla\ ref {Eq5.1.1} para obtener\[f : −7→ 2(−7) \nonumber \] o equivalentemente,\[f : −7 →−14 \nonumber \]

Ejemplo$\PageIndex{7}$

Dada la regla$f : x → 2x + 3$, contesta la pregunta “¿$f$a dónde envía$8$?”

Solución

Para encontrar donde “$f$envía”$8$, sustituya$8$$x$ en la regla$f : x → 2x + 3$ para obtener\[f :8→ 2(8) + 3 \nonumber \] o equivalentemente,\[f :8→ 19 \nonumber \]

Ejercicio$\PageIndex{7}$

Dada la regla$f : x → 3x−5$, answer the question “where does $f$ send $−2$?”

Contestar: $ f : −2 →−11$

Ejemplo$\PageIndex{8}$

Dada la regla$f : x → x/(x+3)$, contesta la pregunta “¿$f$a dónde envía$−1$?”

Solución

Para encontrar donde “$f$envía”$−1$, sustituya$−1$$x$ en la regla$f : x→ x/(x + 3)$ para obtener\[f :-1 \rightarrow \frac{-1}{-1+3} \nonumber \] o equivalentemente,\[f :-1 \rightarrow-\dfrac{1}{2} \nonumber \]

Ejercicio$\PageIndex{8}$

Dada la regla$f : x → 2x^2 +5x$, answer the question “where does $f$ send $3$?”

Contestar: $f : 3 \rightarrow 33$

En Ejemplos$\PageIndex{7}$ y$\PageIndex{8}$, tenga en cuenta que cada vez que sustituya un valor$x$ en la regla dada, obtiene una respuesta única. Esto significa que cada objeto en el dominio de$f$ se envía a un objeto único en el rango de$f$, haciendo las reglas en Ejemplos$\PageIndex{7}$ y$\PageIndex{8}$ funciones. Esto nos lleva a una descripción detallada de una función.

Regla de tres

Una función consta de tres partes:

un conjunto de objetos que los matemáticos llaman el dominio
un segundo conjunto de objetos que los matemáticos llaman el rango
una regla que describe cómo asignar cada objeto en el dominio a exactamente un objeto en el rango.

Notación de funciones

Aunque la notación del diagrama de mapeo$f : x→ 3−4x$ es bastante fácil de entender, la notación de función estándar utilizada es$f(x)=3−4x$. Con notación de diagrama de mapeo, si queremos responder a la pregunta “¿a dónde$f$ envía$12$?” , escribimos:

\[\begin{array}{c}{f : x \rightarrow 3-4 x} \\ {f : 12 \rightarrow 3-4(12)} \\ {f : 12 \rightarrow 3-48} \\ {f : 12 \rightarrow-45}\end{array} \nonumber \]

De ahí,$f : 12→−45$; es decir,$f$ envía$12$ a$−45$. La notación de funciones usa exactamente el mismo concepto; es decir,$12$ sustituto de$x$.

Consejos para usar la notación de funciones

Reemplazar todas las ocurrencias de variables en la notación con paréntesis abiertos. Dejar espacio entre paréntesis para sustituir el valor dado de la variable.
Sustituir los valores dados de las variables en los paréntesis abiertos preparados en el primer paso.
Evaluar la expresión resultante de acuerdo con el Orden de Operaciones Rector de Reglas.

Dado$f(x)=3−4x$, para evaluar$f(12)$, primero reafirmar la notación de función, luego reemplazar cada ocurrencia de la variable con paréntesis abiertos.

\[\begin{aligned} f(x)&= 3-4 x \quad \color {Red} \text { Original function notation. } \\ f(\; \; ) &= 3-4(\; \; ) \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Ahora sustituya$x$ en$12$ los paréntesis abiertos preparados en el último paso.

\[\begin{aligned} f({\color {Red} 12})&= 3-4({\color {Red} 12}) \quad \color {Red} \text { Substitute } 12 \text { for } x \text { in the open parentheses positions. } \\ f(12) &= 3-48 \quad \color {Red} \text { Multiply. } \\ f(12) &= -45 \quad \color {Red} \text { Subtract. } \end{aligned} \nonumber \]

De ahí,$f(12) =−45$; es decir,$f$ envía$12$ a$−45$.

Ejemplo$\PageIndex{9}$

Dado$f(x)=4−5x−x^2$, evaluar$f(−3)$.

Solución

Comience reemplazando cada ocurrencia de la variable$x$ con paréntesis abiertos.

\[\begin{aligned} f(x) &=4-5 x-x^{2} \quad \color {Red} \text { Original function notation. }\\ f( & )=4-5(\quad)-(\quad)^{2} \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Ahora sustituya$x$ en$−3$ los paréntesis abiertos preparados en el último paso.

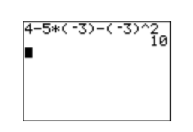
\[\begin{aligned} f({\color {Red}-3}) &= 4-5({\color {Red}-3})-({\color {Red}-3})^{2} \quad \color {Red} \text { Substitute }-3 \text { for } x \text { in the open parentheses positions. } \\ f(-3) &= 4-5(-3)-9 \quad \color {Red} \text { Evaluate exponent: }(-3)^{2}=9 \\ f(-3) &= 4+15-9 \quad \color {Red}\text { Multiply: }-5(-3)=15\\ f(-3) &= 10 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]

Por lo tanto,$f(−3) = 10$. Consulta esto en tu calculadora (ver Figura$\PageIndex{9}$).

higo 5.1.9.png — Figura$\PageIndex{9}$: Comprobación de la calculadora.

El siguiente ejemplo demuestra una de las ventajas de la notación de funciones. Por ejemplo, es fácil hacer referencia a la función en la que se quiere sustituir el$x$ -value dado.

Ejemplo$\PageIndex{10}$

Dado$f(x)=5−x$ y$g(x)=x^2 −9$, encontrar$f(−1)$ y$g(−2)$.

Solución

Se nos dan dos deﬁniciones de función,$f$ y$g$, pero primero se nos pide que lo busquemos$f(−1)$. Esto significa que debemos reemplazar cada ocurrencia de$x$ con$−1$ en la función$f(x)=5−x$.

\[\begin{aligned} f(x) &= 5-x \quad \color {Red} \text { Original function notation. } \\ f(\;\;) &= 5-(\;\;) \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Ahora sustituya$x$ en$−1$ los paréntesis abiertos preparados en el último paso.

\[\begin{aligned} f(-1) &= 5-(-1) \quad \color {Red} \text { Substitute }-1 \text { for } x \text { in the open } \\ &= 5+1 \quad \color {Red}\text { Add the opposite. } \\ &= 6 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]

Por lo tanto,$f(−1) = 6$. A continuación se nos pide que busquemos$g(−2)$. Esto significa que debemos reemplazar cada ocurrencia de$x$ con$−2$ en la función$g(x)=x^2 −9$.

\[\begin{aligned} g(x) &= x^{2}-9 \quad \color {Red} \text { Original function notation. } \\ g(\;\;) &= (\;\;)^{2}-9 \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Ahora sustituya$x$ en$−2$ los paréntesis abiertos preparados en el último paso.

\[\begin{aligned} g({\color {Red}-2}) &= ({\color {Red}-2})^{2}-9 \quad \color {Red} \text { Substitute }-2 \text { for } x \text { in the open parentheses position. } \\ &= 4-9 \quad \color {Red} \text { Exponent first: }(-2)^{2}=4 \\ &= -5 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]

Por lo tanto,$g(−2) =−5$.

Ejercicio$\PageIndex{10}$

Dado f$(x)=3x^2 −20$ and $g(x)=4x +6/x$, ﬁnd$f(−3)$ and $g(2)$.

Contestar: $f(−3) = 7$y$g(2) = 10$

Intercambiar$y$ y$f(x)$

En la mayoría de los casos,$y$ y$f(x)$ son completamente intercambiables. Por ejemplo, compara y contrasta los siguientes dos ejemplos.

Pregunta: Dado$y =3 x + 7$, encontrar$y$ cuando$x$ es igual$5$.

Solución: Reemplazar$x$ con$5$.

\[\begin{array}{l}{y=3 x+7} \\ {y=3(5)+7} \\ {y=15+7} \\ {y=22}\end{array} \nonumber \]

Pregunta: Dado$f(x)=3 x + 7$, evaluar$f(5)$

Solución: Reemplazar$x$ con$5$.

\[\begin{array}{l}{f(x)=3 x+7} \\ {f(5)=3(5)+7} \\ {f(5)=15+7} \\ {f(5)=22}\end{array} \nonumber \]

En cada caso, la respuesta es$22$. Sin embargo, en el primer caso, la respuesta$y = 22$ disfraza el hecho de que$5$ se utilizó un$x$ -valor de para llegar al resultado. Por otro lado, cuando usamos notación de función, la respuesta final$f(5) = 22$ indica que usamos un$x$ -valor de$5$ para determinar que el$y$ -value es$22$. Esta es otra ventaja de la notación de funciones.

Veamos una aplicación final que demuestra que$y$ y$f(x)$ son intercambiables.

Ejemplo$\PageIndex{11}$

Esbozar la gráfica de$f(x)=2x−3$.

Solución

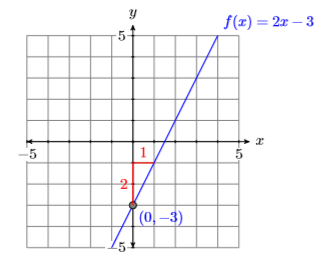
Porque$y$ y$f(x)$ son intercambiables, la instrucción es idéntica a “bosquejar la gráfica de”$y =2 x−3$. La gráfica es una línea, con pendiente$2$ e$y$ -intercepción en$(0,−3)$. Trace la$y$ -intercepción en$(0,−3)$, luego mueva hacia arriba$2$ y$1$ hacia la derecha para crear una línea con pendiente$2$ (ver Figura$\PageIndex{10}$). Observe cómo hemos etiquetado la gráfica con su ecuación usando la notación de funciones.

higo 5.1.10.png — Figura$\PageIndex{10}$: La gráfica de$f(x)=2x−3$ es una línea.

Ejercicio$\PageIndex{11}$

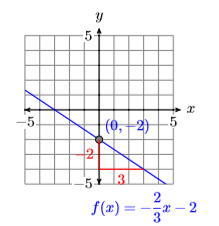
Esbozar el gráfico de$f(x)=-\dfrac{2}{3} x-2$

Contestar: $Ex 5.1.11.png$

Search

Text Color

Text Size

Margin Size

Font Type

Diagramas de mapeo

Deﬁnición de la función

Notación de diagrama de mapeo

Notación de funciones

Intercambiar\(y\) y\(f(x)\)