5.2: Polinomios

Última actualización
Guardar como PDF

Page ID: 111677

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Comenzamos con la definición de un término.

Definición: Término

Un término es un solo número (llamado término constante) o el producto de un número y una o más variables.

Por ejemplo, cada uno de los siguientes es un término.

\[ -5 \quad-3 x^{2} \quad 12 y^{2} z^{3} \quad 13 a^{2} b c^{3} \nonumber \]

Observe cómo el primer término es un solo número, mientras que los términos restantes son productos de un número y una o más variables. Por ejemplo,$−3x^2$ es el producto de$−3$,$x$, y$x$.

Definición: Coecient

Cuando un término es un producto de un número y una o más variables, el número se denomina coeciente del término. En el caso de un término que sea un solo número, el número en sí se llama coeciente.

Así, por ejemplo, los coecientes de los términos\[-5 \quad-3 x^{2} \quad 12 y^{2} z^{3} \quad 13 a^{2} b c^{3} \nonumber \] son$−5$,$−3$,$12$, y$13$, respectivamente.

Definición: Grado

El grado de un término es la suma de los exponentes en cada variable del término. Un término constante (número único sin variables) tiene grado cero.

Así, por ejemplo, los grados de los términos\[-5 \quad-3 x^{2} \quad 12 y^{2} z^{3} \quad 13 a^{2} b c^{3} \nonumber \] son$0$,$2$,$5$, y$6$, respectivamente. En el último ejemplo, tenga en cuenta que$13a^2bc^3$ es equivalente a$13a^2b^1c^3$, por lo que sumando exponentes, obtenemos:

\[\begin{aligned} \text { Degree of } 13 a^{2} b c^{3} &=\text { Degree of } 13 a^{2} b^{1} c^{3} \\ &=2+1+3 \\ &=6 \end{aligned} \nonumber \]

Definición: Monomial

Las palabras monomial y término son equivalentes.

Así,\[-5 \quad-3 x^{2} \quad 12 y^{2} z^{3} \quad 13 a^{2} b c^{3} \nonumber \] son los monomios.

Definición: Binomial

Un binomio es una expresión matemática que contiene exactamente dos términos, separados por signos más o menos.

Por ejemplo, cada una de las expresiones matemáticas\[2 x+3 y \quad-3 a^{2}-3 b^{2} \quad x y+7 \quad-3 x^{2} y+5 x y^{2} \nonumber \] es un binomio. Cada expresión tiene exactamente dos términos.

Definición: Trinomial

Un trinomio es una expresión matemática que contiene exactamente tres términos, separados por signos más o menos.

Por ejemplo, cada una de las expresiones matemáticas\[2 x^{2}+3 x+7 \quad a^{2}+2 a b+b^{2} \quad x^{4}-2 x^{2} y^{2}+3 y^{4} \nonumber \] es un trinomio. Cada expresión tiene exactamente tres términos.

Una bicicleta tiene dos ruedas, un binomio tiene dos términos. Un triciclo tiene tres ruedas, un trinomio tiene tres términos. Pero una vez que superamos los tres términos, cesa la asignación de nombres especiales y usamos la palabra genérica polinomio, que significa “muchos términos”.

Definición: Polinomio

Un polinomio es una expresión matemática muy denominada, con términos separados por signos más o menos. Los coecientes de un polinomio son los coecientes de sus términos.

Cada una de las expresiones anteriores,\[12 y^{2} z^{3} \quad-3 a^{2}-3 b^{2} \quad x^{4}-2 x^{2} y^{2}+3 y^{4} \nonumber \] aunque se les asignaron los nombres particulares monomial, binomial y trinomio, respectivamente, también son expresiones “muchas denominadas” y también pueden llamarse polinomios. Sin embargo, debido a que la palabra polinomio significa “muchos términos”, también podemos usar la palabra polinomio para describir expresiones matemáticas con más de tres términos, tales como:\[x^{4}-4 x^{3} y+6 x^{2} y^{2}-4 x y^{3}+y^{4} \nonumber \] Los coedecientes de$x^{4}-4 x^{3} y+6 x^{2} y^{2}-4 x y^{3}+y^{4}$ are$1$,$−4$,$6$,$−4$, y$1$.

Poderes ascendentes y descendentes

Cuando se nos pide simplificar una expresión polinómica, debemos combinar cualquier término similar que encontremos, y cuando sea posible, organizar la respuesta en potencias ascendentes o descendentes.

Ejemplo$\PageIndex{1}$

Simplifica la siguiente expresión polinómica, ordenando tu respuesta en los poderes descendentes de$x$. Una vez que hayas completado esa tarea, haz un segundo arreglo, ordenando tus términos en poderes ascendentes de$x$. \[2 x^{3}+7 x-3 x^{2}+11 x+8 x^{2}+11+15 x \nonumber \]

Solución

Para arreglar nuestra respuesta en potencias descendentes de$x$, queremos colocar el término con el poder más alto de$x$ primero y el término con el poder más bajo del$x$ último. Usamos las propiedades conmutativas y asociativas para cambiar el orden y reagruparnos, luego combinamos términos similares.

\[\begin{aligned} 2 x^{3}+7 x &-3 x^{2}+11 x+8 x^{2}+11+15 x \\ &=2 x^{3}+\left(-3 x^{2}+8 x^{2}\right)+(7 x+11 x+15 x)+11 \\ &=2 x^{3}+5 x^{2}+33 x+11 \end{aligned} \nonumber \]

Observe cómo los poderes de$x$ comenzar en$3$, luego bajan en orden.

Para organizar nuestra respuesta final en poderes ascendentes de$x$, ponemos el poder más bajo de$x$ primero, luego el poder más alto del$x$ último, reagrupando y combinando términos similares.

\[\begin{aligned} 2 x^{3}+7 x &-3 x^{2}+11 x+8 x^{2}+11+15 x \\ &=11+(7 x+11 x+15 x)+\left(-3 x^{2}+8 x^{2}\right)+2 x^{3} \\ &=11+33 x+5 x^{2}+2 x^{3} \end{aligned} \nonumber \]

Obsérvese cómo empezamos con el término constante, luego los poderes de$x$ incremento en orden.

Ejercicio$\PageIndex{1}$

Simplifique el siguiente polinomio, y organice su respuesta en poderes ascendentes de\[3 x^{2}-5 x^{3}+8 x+9 x^{2}-7 x+2 x^{3} \nonumber \]

Responder: $x+12 x^{2}-3 x^{3}$

Cuando tenemos un polinomio en una sola variable, como el polinomio en Ejemplo$\PageIndex{1}$, disponer los términos en orden ascendente o descendente es bastante sencillo. Sin embargo, un polinomio en dos o más variables es un poco más difícil, y a veces imposible, de organizar en un orden decente.

Ejemplo$\PageIndex{2}$

Simplifique la siguiente expresión polinómica, luego organice su respuesta en poderes descendentes de$x$. \[x^{3}+2 x y^{2}-6 x^{2} y+y^{3}-3 x y^{2}+4 x^{2} y \nonumber \]

Solución

Nuevamente usaremos las propiedades conmutativas y asociativas para cambiar el orden y reagruparnos, poniendo los términos con los poderes más altos de$x$ primero, luego seguiremos con términos que contengan potencias inferiores de$x$ en orden.

\[\begin{aligned} x^{3}+2 x y^{2} &-6 x^{2} y+y^{3}-3 x y^{2}+4 x^{2} y \\ &=x^{3}+\left(-6 x^{2} y+4 x^{2} y\right)+\left(2 x y^{2}-3 x y^{2}\right)+y^{3} \\ &=x^{3}-2 x^{2} y-x y^{2}+y^{3} \end{aligned} \nonumber \]

Obsérvese que este es un orden muy natural, los poderes de$x$ disminuir mientras que simultáneamente los poderes de$y$ aumento.

Ejercicio$\PageIndex{2}$

Simplifique el siguiente polinomio, y organice su respuesta en potencias descendentes de$x$:\[-4 x^{2} y^{2}+3 x y^{3}+6 x^{3} y-x y^{3}+2 x^{2} y^{2} \nonumber \]

Responder: $6 x^{3} y-2 x^{2} y^{2}+2 x y^{3}$

No todos los ejemplos tendrán un buen orden presentado en Ejemplo$\PageIndex{2}$, con las potencias de una variable descendiendo mientras que las potencias de la otra variable ascienden simultáneamente. A veces tenemos que hacer algunas elecciones muy subjetivas sobre el orden de los términos.

Ejemplo$\PageIndex{3}$

Simplifique la siguiente expresión polinómica, luego organice su respuesta en algún tipo de orden razonable. \[a^{3} b^{3}+2 a^{2} b-3 a^{2} b^{3}+4 a^{3} b^{3}+5 a^{4}+3 a^{2} b+b^{5} \nonumber \]

Solución

Tratemos de arreglar los términos para que los poderes de un desciendan. Nuevamente, utilizamos las propiedades conmutativas y asociativas para cambiar el orden y reagruparnos.

\[\begin{aligned} a^{3} b^{3}+2 a^{2} b &-3 a^{2} b^{3}+4 a^{3} b^{3}+5 a^{4}+3 a^{2} b+b^{5} \\ &=5 a^{4}+\left(a^{3} b^{3}+4 a^{3} b^{3}\right)+\left(2 a^{2} b+3 a^{2} b\right)-3 a^{2} b^{3}+b^{5} \\ &=5 a^{4}+5 a^{3} b^{3}+5 a^{2} b-3 a^{2} b^{3}+b^{5} \end{aligned} \nonumber \]

Obsérvese que en nuestro arreglo$a$ final, los poderes de descender, pero los poderes de$b$ rebotar arriba y abajo, pero al menos tenemos los poderes de$a$ descender. Eso debería ayudarnos a detectar si nos hemos perdido un término al tiempo que simplificamos el problema dado.

Ejercicio$\PageIndex{3}$

Simplifique el siguiente polinomio, y organice su respuesta en poderes ascendentes de$b$: \[5 a^{3} b^{2}+4 a b^{3}-2 a^{2} b+3 a^{3} b^{2}-a b^{3} \nonumber \]

Responder: $-2 a^{2} b+8 a^{3} b^{2}+3 a b^{3}$

El grado de un polinomio

Para encontrar el grado de un polinomio, ubicar el término del polinomio que tiene el grado más alto.

El grado de un polinomio

El grado de un polinomio es el grado del término que tiene el grado más alto.

Encontrar el grado de polinomio de una sola variable es bastante fácil.

Ejemplo$\PageIndex{4}$

¿Cuál es el grado del polinomio$x^{3}-4 x^{2}+5-6 x+2 x^{7}$?

Solución

Primero, arreglemos el polinomio en potencias descendentes de x.

\[2 x^{7}+x^{3}-4 x^{2}-6 x+5 \nonumber \]

Organizar el polinomio en potencias descendentes de$x$ hace más fácil ver que el término del polinomio con el grado más alto es$2x^7$. Por lo tanto, el grado del polinomio es$7$.

Ejercicio$\PageIndex{4}$

¿Cuál es el grado del polinomio$2 x^{3}+8 x^{2}+3 x^{4}+2 x+10$?

Responder: $4$

Encontrar el grado de polinomio de más de una variable es un poco más complicado.

Ejemplo$\PageIndex{5}$

¿Cuál es el grado del polinomio$x^{4}-2 x^{3} y^{7}+y^{5}$?

Solución

Obsérvese que el polinomio ya está dispuesto en potencias descendentes de$x$, un arreglo que probablemente sea tan bueno como lo vamos a conseguir. En la siguiente tabla, enumeramos el grado de cada término. Recuerde, el grado de cualquier término se encuentra sumando los exponentes en sus variables.

\[\begin{array}{cc}{\text { Term }} & {\text { Degree }} \\ \hline x^{4} & {4} \\ {-2 x^{3} y^{7}} & {10} \\ {y^{5}} & {5} \\ \hline\end{array} \nonumber \]

De ahí que el término con mayor grado sea$-2 x^{3} y^{7}$, haciendo$10$ el grado del polinomio.

Ejercicio$\PageIndex{5}$

¿Cuál es el grado del polinomio$x^{2} y^{4}-6 x^{2} y^{2}+5 x^{2} y^{5}-2 x y$?

Responder: $7$

Funciones polinómicas

Primero definimos lo que queremos decir con una función polinómica.

Función polinomial

Una función polinómica es una función determinada por una regla que asigna a cada objeto de dominio un objeto de rango definido por una expresión polinómica.

Los cursos avanzados, como el cálculo multivariado, utilizan frecuentemente funciones polinómicas de más de una variable como$f(x, y)=x^{2}+y^{2}$. Sin embargo, en este curso, nuestro enfoque estará en las funciones polinómicas de una sola variable, como$p(x)=3-4 x-9 x^{2}$ y$q(x)=x^{3}-9 x^{2}+11$.

Ejemplo$\PageIndex{6}$

Dada la función polinomial$p(x)=x^{3}-8 x-11$, evaluar$p(−3)$.

Solución

Para evaluar$p(−3)$, primero reinicie la definición de la función, luego reemplace cada ocurrencia de la variable$x$ con paréntesis abiertos.

\[\begin{aligned} p(x) &= x^{3}-8 x-11 \quad \color {Red} \text { Original function definition. } \\ p(\;\;) &= (\;\;)^{3}-8(\;\;)-11 \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

A continuación, sustituya$−3$$x$ en los paréntesis abiertos preparados en el último paso.

\[\begin{aligned} p(-3) &= (-3)^{3}-8(-3)-11 \quad \color {Red} \text { Substitute }-3 \text { for } x \text { in the open parentheses positions.} \\ p(-3) &= -27-8(-3)-11 \quad \color {Red} \text { Exponent first: }(-3)^{3}=-27 \\ p(-3) &= -27+24-11 \quad \color {Red} \text { Multiply: }-8(-3)=24 \\ p(-3) &= -14 \quad \color {Red} \text { Add. } \end{aligned} \nonumber \]

De ahí,$p(−3) = −14$. Puedes verificar fácilmente este resultado en tu calculadora (ver Figura$\PageIndex{1}$).

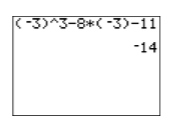
higo 5.2.1.png — Figura$\PageIndex{1}$: Comprobación de la calculadora.

Ejercicio$\PageIndex{6}$

Dada la función polinómica$p(x)=-3 x^{2}+7 x+4$, evaluar$p(2)$.

Responder: $6$

La Gráfica de una Función Polinómica

Una de las funciones polinómicas más importantes en todas las matemáticas y ciencias es el polinomio que tiene grado dos.

Polinomio cuadrático

El polinomio de segundo grado que tiene la forma\[p(x)=a x^{2}+b x+c \nonumber \] se llama polinomio cuadrático. La gráfica de este polinomio se llama parábola.

La parábola tiene aproximadamente forma de U. Algunos se abren hacia arriba, otros se abren hacia abajo, dependiendo del signo del término principal.

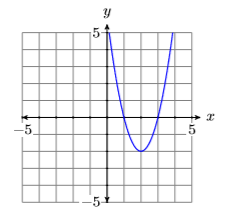
En Figura$\PageIndex{2}$, el término principal de la parábola$p(x)=2 x^{2}-8 x+6$ tiene dos positivos como su coecient, por lo que se abre hacia arriba.

higo 5.2.2.png — Figura$\PageIndex{2}$: La gráfica de$p(x)=2 x^{2}-8 x+6$ se abre.

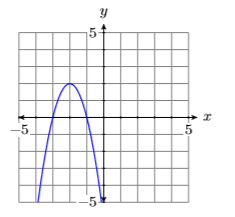
En Figura$\PageIndex{3}$, el término principal de la parábola$p(x)=-2 x^{2}-8 x-6$ tiene dos negativos como su coeciente, por lo que se abre hacia abajo.

higo 5.2.3.png — Figura$\PageIndex{3}$: La gráfica de$p(x)=-2 x^{2}-8 x-6$ se abre hacia abajo.

Nota

El signo del término principal de$p(x)=ax^2 +bx+c$ determina si la parábola se abre hacia arriba o hacia abajo.

Si$a>0$, la parábola se abre hacia arriba.
Si$a<0$, la parábola se abre hacia abajo.

El punto de inflexión de una parábola tiene un nombre especial.

El vértice de una parábola

La gráfica del polinomio de segundo grado$p(x)=ax^2+bx+c$ tiene un único punto de inflexión, llamado el vértice de la parábola.

Ejemplo$\PageIndex{7}$

Usa tu calculadora gráfica para bosquejar la gráfica del polinomio cuadrático$p(x)=−3x^2 + 12x + 25$.

Solución

El grado del polinomio$p(x)=−3x^2 + 12x + 25$ es dos, por lo que es un polinomio cuadrático y su gráfica es una parábola. Además, su término principal tiene tres negativos como su coecient, por lo que sabemos que la parábola se abre hacia abajo. Ingrese$y = −3x^2 + 12x + 25$ como$Y 1=-3 * X \wedge 2+12 * X+25$ en el menú Y= (vea la primera imagen en la Figura$\PageIndex{4}$), luego seleccione 6:ZEstándar en el menú ZOOM para producir la tercera imagen en la Figura$\PageIndex{4}$.

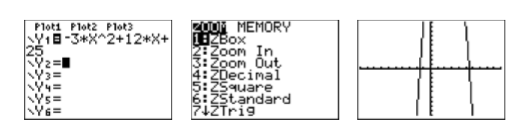
higo 5.2.4.png — Figura$\PageIndex{4}$: Dibujando la gráfica de$p(x)=−3x^2 + 12x + 25$.

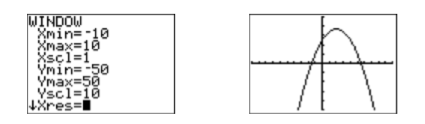
Obsérvese que la gráfica de la Figura$\PageIndex{4}$ parece tener la forma de U de una parábola que se abre hacia abajo. Su vértice (punto de inflexión) no es visible, pero uno conjeturaría que se encuentra en la parte superior de la pantalla. Necesitamos ajustar los parámetros WINDOW para que el vértice de la parábola sea visible en la pantalla de visualización. Después de alguna experimentación, nos establecemos en los parámetros mostrados en la primera imagen de la Figura$\PageIndex{5}$, luego presionamos el botón GRAPH para producir la segunda imagen en la Figura$\PageIndex{5}$.

higo 5.2.5.png — Figura$\PageIndex{5}$: Ajusta los parámetros de **VENTANA** para que el vértice sea visible en la pantalla de visualización.

Al informar su resultado en su tarea, siga las Directrices para el envío de la calculadora del Capítulo 3, Sección2.

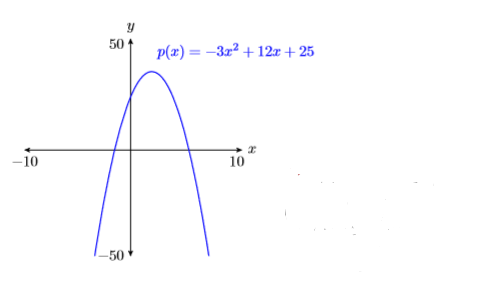
$higo 5.2.5a.png$

Dibuja ejes con una regla.
Etiquete el eje horizontal$x$ y el eje vertical$y$.
Indique los parámetros WINDOW$\mathrm{Xmin}, \mathrm{Xmax}, \mathrm{Ymin}$, y$\mathrm{Ymax}$\) al final de cada eje.
A mano alzada la curva y etiquetarla con su ecuación.

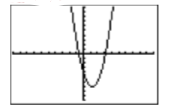
Ejercicio$\PageIndex{7}$

Usa tu calculadora gráfica para bosquejar la gráfica del polyno mial cuadrático$p(x)=2x^2 −5x−4$.

Responder: $Ex 5.2.7.png$

Cuando el grado del polinomio es mayor que dos, el número de puntos de inflexión de la gráfica podría aumentar. Esto hace que algunas curvas sean muy interesantes. En cursos más avanzados, como álgebra intermedia y universitaria, se te presentará una variedad de técnicas que te ayudarán a determinar las ventanas de visualización adecuadas para las gráficas de estos polinomios de grado superior. No obstante, en esta sección introductoria, te ayudaremos sugiriendo una buena ventana de visualización para cada polinomio, una que te permitirá ver todos los puntos de inflexión de la gráfica del polinomio.

Ejemplo$\PageIndex{8}$

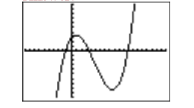
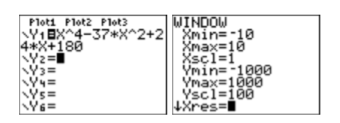
Usa tu calculadora gráfica para bosquejar el gráfico de la función polinómica$p(x)=x^{4}-37 x^{2}+24 x+180$. Establezca los parámetros de su ventana de la siguiente manera:$\mathbf{X} \min =-10, \mathbf{X} \max =10, \mathbf{X} \operatorname{scl}=1, \mathbf{Y} \min =-1000, \mathbf{Y} \max = 1000,$ y$\mathbf{Y} \operatorname{scl} =100$.

Solución

Ingrese la función polinómica en$\mathbf{Y} \mathbf{1}$ del menú Y=, luego ingrese los parámetros de ventana sugeridos en el menú VENTANA (ver Figura$\PageIndex{6}$).

higo 5.2.6.png — Figura$\PageIndex{6}$: Ingresa el polinomio y ajusta los parámetros de VENTANA.

Presione el botón GRAPAR en la fila superior de su calculadora para producir la gráfica de la función polinómica que se muestra en la Figura$\PageIndex{7}$.

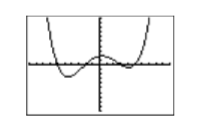
higo 5.2.7.png — Figura$\PageIndex{7}$: La gráfica de$p(x)=x^4 −37x^2 + 24x + 180$.

¡Curva de aspecto dulce!

Ejercicio$\PageIndex{8}$

Usa tu calculadora gráfica para bosquejar la gráfica del polinomio cuadrático p (x) =x3 −14x2 + 20x + 60. Establezca los parámetros de su ventana de la siguiente manera:$\mathbf{X} \min =-10, \mathbf{X} \max =20, \mathbf{X} \operatorname{scl}=1, \mathbf{Y} \min =-200, \mathbf{Y} \max = 200,$ y$\mathbf{Y} \operatorname{scl} =20$.

Responder: $Ex 5.2.8.png$

Search

Text Color

Text Size

Margin Size

Font Type