5.3: Aplicaciones de polinomios

Última actualización
Guardar como PDF

Page ID: 111688

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En esta sección investigamos las aplicaciones del mundo real de las funciones polinómicas.

Ejemplo$\PageIndex{1}$

El precio promedio de un galón de gas al inicio de cada mes para el periodo que inicia en noviembre de 2010 y termina en mayo de 2011 se dan en el margen. Los datos se trazan en la Figura$\PageIndex{1}$ y se fijan con el siguiente polinomio de tercer grado, donde t es el número de meses que han pasado desde octubre de 2010.

\[p(t)=-0.0080556 t^{3}+0.11881 t^{2}-0.30671 t+3.36 \label{Eq5.3.1} \]

Usa la gráfica y luego el polinomio para estimar el precio de un galón de gas en California en febrero de 2011.

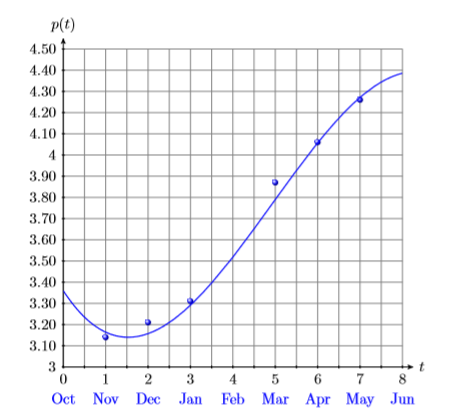
higo 5.3.1.png — Figura$\PageIndex{1}$: Ajuste del precio del gas versus mes con un polinomio cúbico.

\[\begin{array}{c|c}\hline \text { Month } & {\text { Price }} \\ \hline \text { Nov. } & {3.14} \\ {\text { Dec. }} & {3.21} \\ {\text { Jan }} & {3.31} \\ {\text { Mar. }} & {3.87} \\ {\text { Apr. }} & {4.06} \\ {\text { May }} & {4.26} \\ \hline\end{array} \nonumber \]

Solución

Localizar Febrero ($t = 4$) en el eje horizontal. A partir de ahí, dibuje una flecha vertical hacia arriba hasta la gráfica, y desde ese punto de intersección, una segunda flecha horizontal sobre el eje vertical (ver Figura$\PageIndex{2}$). Parecería que el precio por galón en febrero era aproximadamente$\$3.51$.

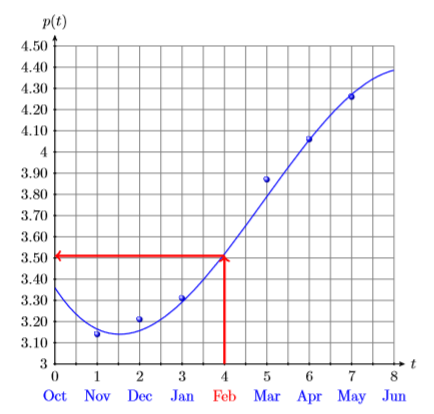
higo 5.3.2.png — Figura$\PageIndex{2}$: Aproximación del precio del gas durante febrero.

A continuación, utilizaremos el polinomio de tercer grado fitted para aproximar el precio por galón para el mes de febrero de 2011. Comience con la función determinada por la ecuación\ ref {Eq5.3.1} y sustituya$4$$t$.

\[\begin{aligned} p(t) &=-0.0080556 t^{3}+0.11881 t^{2}-0.30671 t+3.36 \\ p(4) &=-0.0080556(4)^{3}+0.11881(4)^{2}-0.30671(4)+3.36 \end{aligned} \nonumber \]

Utilice la calculadora para evaluar$p(4)$ (ver Figura$\PageIndex{3}$). Redondeo al más cercano

higo 5.3.3.png — Figura$\PageIndex{3}$: Evaluando$p(4)$.

centavo, el precio en febrero era$\$3.52$ por galón.

Ejemplo$\PageIndex{2}$

Si un proyectil se enciende en el aire, su altura sobre el suelo en cualquier momento viene dada por la fórmula

\[y=y_{0}+v_{0} t-\dfrac{1}{2} g t^{2} \label{Eq5.3.2} \]

donde

$y$= altura sobre el suelo en el momento$t$

$y_0$= altura inicial sobre el suelo en el momento$t = 0$

$v_0$= velocidad inicial en el tiempo$t = 0$

$g$= aceleración por gravedad

$t$= el tiempo transcurrido desde el lanzamiento del proyectil

Si se lanza un proyectil con una velocidad inicial de$100$ metros por segundo ($100$m/s) desde una azotea$8$ a metros ($8$m) sobre el nivel del suelo, ¿en qué momento alcanzará el proyectil primero una altura de$400$ metros ($400$m)? Nota: Cerca de la superficie terrestre, la aceleración debida a la gravedad es aproximadamente$9.8$ metros por segundo por segundo ($9.8$(m/s) /s o$9.8$ m/s ²).

Solución

Se nos da la altura inicial es$y_0 = 8$ m, la velocidad inicial es$v_0 = 100$ m/s, y la aceleración por gravedad es$g =9.8$ m/s ². Sustituya estos valores en la Ecuación\ ref {Eq5.3.2}, luego simplifique para producir el siguiente resultado:

\[\begin{array}{l}{y=y_{0}+v_{0} t-\dfrac{1}{2} g t^{2}} \\ {y=8+100 t-\dfrac{1}{2}(9.8) t^{2}} \\ {y=8+100 t-4.9 t^{2}}\end{array} \nonumber \]

Ingrese$y=8+100 t-4.9 t^{2}$ como$\mathbf{Y} \mathbf{1}=\mathbf{8}+100^{*} \mathbf{X}-4.9^{*} \mathbf{X} \wedge \mathbf{2}$ en el menú Y= (vea la primera imagen en la Figura$\PageIndex{4}$). Después de alguna experimentación, nos fijamos en los parámetros VENTANA mostrados en la segunda imagen de la Figura$\PageIndex{4}$. Pulsa el botón GRAPH para producir la gráfica de la figura$y=8+100 t-4.9 t^{2}$ mostrada en la tercera imagen$\PageIndex{4}$.

En este ejemplo, el eje horizontal es en realidad el$t$-axis. So when we set $\mathrm{Xmin}$ and $\mathrm{Xmax}$, we’re actually setting bounds on the $t$-axis.

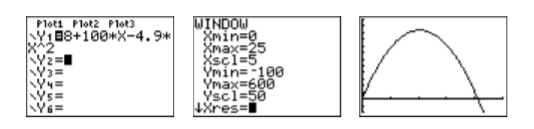
higo 5.3.4.png — Figura$\PageIndex{4}$: Croquizar la gráfica de$y = 8 + 100t−4.9t^2$.

Para encontrar cuando el proyectil alcanza una altura de$400$ metros ($400$m), sustituya$400$$y$ para obtener:

\[400=8+100 t-4.9 t^{2} \label{Eq5.3.3} \]

Ingrese el lado izquierdo de la Ecuación\ ref {Eq5.3.3} en$\mathbf{Y} \boldsymbol{2}$ en el menú Y=, como se muestra en la primera imagen de la Figura$\PageIndex{5}$. Pulse el botón GRAPH para producir el resultado mostrado en la segunda imagen de la Figura$\PageIndex{5}$. Tenga en cuenta que hay dos puntos de intersección, lo cual tiene sentido ya que el proyectil golpea$400$ metros en el camino hacia arriba y$400$ metros en el camino hacia abajo.

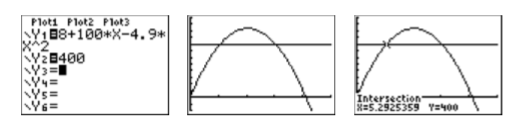
higo 5.3.5.png — Figura$\PageIndex{5}$: Determinar cuándo el primer objeto alcanza los$400$ metros.

Para encontrar el primer punto de intersección, seleccione 5:intersectar en el menú CALC. Presione INTRO en respuesta a “Primera curva”, luego presione ENTRAR nuevamente en respuesta a “Segunda curva”. Para tu conjetura, usa las teclas de flecha para acercar el cursor al primer punto de intersección que al segundo. En este punto, presione ENTRAR en respuesta a “Guess”. El resultado se muestra en la tercera imagen de la Figura$\PageIndex{5}$. El primer proyectil alcanza una altura de$400$ metros aproximadamente$5.2925359$ segundos después del lanzamiento.

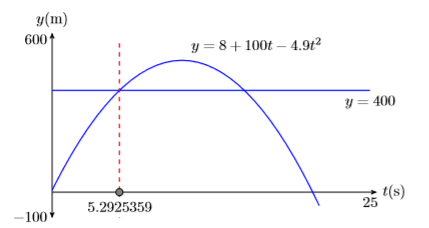
higo 5.3.6.png — Figura$\PageIndex{6}$: Reportando tu solución gráfica en tu tarea.

La parábola mostrada en la Figura$\PageIndex{6}$ is not the actual ﬂight path of the projectile. The graph only predicts the height of the projectile as a function of time.

Reportando la solución en tu tarea: Duplica la imagen en la ventana de visualización de tu calculadora en tu página de tareas. Usa una regla para dibujar todas las líneas, pero a mano alzada cualquier curva.

Etiquete los ejes horizontal y vertical con$t$ y$y$, respectivamente (ver Figura$\PageIndex{6}$). Incluya las unidades (segundos (s) y metros (m)).
Coloca tus parámetros WINDOW al final de cada eje (ver Figura$\PageIndex{6}$). Incluya las unidades (segundos (s) y metros (m)).
Etiquetar cada gráfica con su ecuación (ver Figura$\PageIndex{6}$).
Dibuje una línea vertical discontinua a través del primer punto de intersección. Sombra y etiquete el punto (con su$t$ valor) donde la línea vertical discontinua cruza el$t$ eje. Esta es la primera solución de la ecuación$400 = 8+100t−4.9t^2$ (ver Figura$\PageIndex{6}$).

Redondeando a la décima de segundo más cercana, el proyectil tarda aproximadamente$t ≈ 5.3$ segundos en alcanzar primero una altura de$400$ metros.

La frase “sombrear y etiquetar el punto” significa fillar en el punto del$t$-axis, then write the $t$-value of the point just below the shaded point.

Ejercicio$\PageIndex{2}$

Si se lanza un proyectil con una velocidad inicial$60$ meters per second from a rooftop $12$ meters above ground level, at what time will the projectile de primer alcance una altura de$150$ meters?

Responder: $\approx 3.0693987$segundos

Ceros e$x$ intercepciones de una función

Recordemos eso$f(x)$ y$y$ son intercambiables. Por lo tanto, si se nos pide encontrar dónde una función es igual a cero, entonces necesitamos encontrar los puntos en la gráfica de la función que tienen un$y$ -valor igual a cero (ver Figura$\PageIndex{7}$).

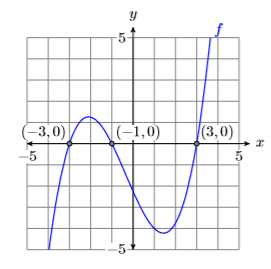
higo 5.3.7.png — Figura$\PageIndex{7}$: Localización de los ceros de una función.

Ceros y$x$-intercepts

Los puntos donde la gráfica fuera cruza el$x$ eje -se denominan las$x$ -intercepciones de la gráfica de$f$. El$x$ -valor de cada$x$ -intercepción se llama cero de la función$f$.

La gráfica de$f$ cruza el$x$ eje -en la Figura$\PageIndex{7}$ en$(−3,0)$,$(−1,0)$, y$(3 ,0)$. Por lo tanto:

Los$x$ -interceptos de f son:$(−3,0)$,$(−1,0)$, y$(3,0)$
Los ceros de$f$ son:$−3$,$−1$, y$3$

Idea clave

Una función es cero donde su gráfica cruza el$x$ eje.

Ejemplo$\PageIndex{3}$

Encuentra los cero (s) de la función$f(x)=1 .5x +5 .25$.

Solución

Recuerda,$f(x)=1 .5x +5 .25$ y$y =1 .5x +5 .25$ son equivalentes. Estamos buscando el valor de$x$ que hace$y = 0$ o$f(x) = 0$. Entonces, comenzaremos con$f(x) = 0$, luego reemplazaremos$f(x)$ con$1 .5x +5 .25$.

\[\begin{aligned} f(x) &= 0 \quad \color {Red} \text { We want the value of } x \text { that makes the function equal to zero. } \\ 1.5 x+5.25 &= 0 \quad \color {Red} \text { Replace } f(x) \text { with } 1.5 x+5.25 \end{aligned} \nonumber \]

Ahora resolvemos para$x$.

\[\begin{aligned} 1.5 x &= -5.25 \quad \color {Red} \text { Subtract } 5.25 \text { from both sides. } \\ x &= \dfrac{-5.25}{1.5} \quad \color {Red} \text { Divide both sides by } 1.5 \\ x &= -3.5 \quad \color {Red} \text { Divide: }-5.25 / 1.5=-3.5 \end{aligned} \nonumber \]

Cheque: Sustituto$−3.5$$x$ en la función$f(x)=1 .5x +5 .25$.

\[\begin{aligned} f(x) &=1.5 x+5.25 \quad \color {Red} \text { The original function. } \\ f(-3.5) &=1.5(-3.5)+5.25 \quad \color {Red} \text { Substitute }-3.5 \text { for } x \\ f(-3.5) &=-5.25+5.25 \quad \color {Red} \text { Multiply: } 1.5(-3.5)=-5.25 \\ f(-3.5) &=0 \quad \color {Red} \text { Add. } \end{aligned} \nonumber \]

Tenga en cuenta que$−3.5$, cuando se sustituye por$x$, hace que la función sea$f(x)=1 .5x+5 .25$ igual a cero. Es por ello$−3.5$ que se llama cero de la función.

Solución de calculadora gráfica: Deberíamos ser capaces de encontrar el cero dibujando la gráfica$f$ y anotando dónde cruza el$x$ eje. Comience cargando la función$f(x)=1 .5x +5 .25$ en$\mathbf{Y1} $ en el menú Y= (vea la primera imagen en la Figura$\PageIndex{8}$).

Seleccione 6:ZStandard en el menú ZOOM para producir la gráfica de$f$ (ver la segunda imagen en la Figura$\PageIndex{8}$). Presiona 2ND CALC para abrir el menú CALCULAR (ver la tercera imagen en la Figura$\PageIndex{8}$). Para encontrar el cero de la función$f$:

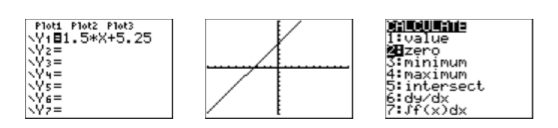
higo 5.3.8.png — Figura$\PageIndex{8}$: Encontrar el cero de$f(x)=1 .5x +5 .25$.

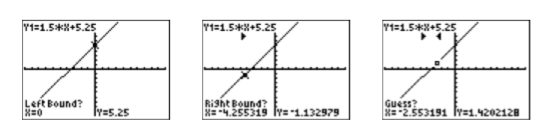
Seleccione 2:cero en el menú CALCULAR. La calculadora responde pidiendo un “¿Izquierda?” (ver la primera imagen en la Figura$\PageIndex{9}$). Use el botón de flecha izquierda para mover el cursor de manera que quede a la izquierda$x$ de la intersección de$f$ y presione ENTRAR.
La calculadora responde pidiendo un “¿Encuadernado a la derecha?” (ver la segunda imagen en la Figura$\PageIndex{9}$). Use el botón de flecha derecha para mover el cursor de manera que quede a la derecha$x$ de la intersección de$f$ y presione ENTRAR.
La calculadora responde pidiendo un “¿Adivina?” (ver la tercera imagen en la Figura$\PageIndex{9}$). Siempre y cuando su cursor se encuentre entre las marcas de borde izquierdo y derecho en la parte superior de la pantalla (vea la tercera imagen en la Figura$\PageIndex{9}$), tiene una conjetura válida. Dado que el cursor ya se encuentra entre los límites izquierdo y derecho, simplemente presione ENTRAR para usar la posición actual del cursor como su suposición.

higo 5.3.9.png — Figura$\PageIndex{9}$: Usando **2:cero** del menú **CALCULAR**.

La calculadora responde aproximando el cero de la función como se muestra en la Figura$\PageIndex{10}$.

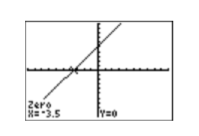
higo 5.3.10.png — Figura$\PageIndex{10}$: $−3.5$es un cero apagado.

Tenga en cuenta que la aproximación encontrada usando la calculadora concuerda muy bien con el cero encontrado usando la técnica algebraica.

Ejercicio$\PageIndex{3}$

Encuentra el (los) cero (s) de la función$f(x)=2 .6x−9.62$.

Responder: $3.7$

Ejemplo$\PageIndex{4}$

¿Cuánto tiempo tardará el proyectil en Ejemplo en volver$\PageIndex{2}$ al nivel del suelo?

Solución

En Ejemplo$\PageIndex{2}$, la altura del proyectil sobre el suelo en función del tiempo viene dada por la ecuación\[y = 8 + 100t−4.9t^2 \nonumber \] Cuando el proyectil regresa al suelo, su altura sobre el suelo será de cero metros. Para encontrar el momento en que esto sucede, sustituya$y = 0$ en la última ecuación y resuelva por$t$. \[0 = 8 + 100t−4.9t^2 \nonumber \]Ingrese la ecuación$y = 8 + 100t − 4.9t^2$ en$\mathbf{Y1} $ en el menú Y= de su calculadora (vea la primera imagen en la Figura$\PageIndex{11}$), luego establezca los parámetros VENTANA que se muestran en la segunda imagen de la Figura$\PageIndex{11}$. Pulse el botón GRAPH para producir la gráfica de la función que se muestra en la tercera imagen de la Figura$\PageIndex{11}$.

higo 5.3.11.png — Figura$\PageIndex{11}$: Croquizar la gráfica de$y = 8 + 100t−4.9t^2$.

En este ejemplo, el eje horizontal es en realidad el$t$-axis. So when we set $\mathrm{Xmin}$ and $\mathrm{Xmax}$, we’re actually setting bounds on the $t$-axis.

Para encontrar el momento en que el proyectil vuelve al nivel del suelo, necesitamos encontrar donde la gráfica de$y = 8+100t−4.9t^2$ cruza el eje horizontal (en este caso el eje t). Seleccione 2:cero en el menú CALC. Use las teclas de flecha para mover el cursor ligeramente hacia la izquierda$t$ de la intersección, luego presione ENTRAR en respuesta a “Límite izquierdo”. Mueva el cursor ligeramente a la derecha de la intersección en T, luego presione ENTRAR en respuesta a “Límite a la derecha”. Deja tu cursor donde está y presiona ENTRAR en respuesta a “Guess”. El resultado se muestra en la Figura$\PageIndex{11}$.

Etiquete los ejes horizontal y vertical con$t$ y$y$, respectivamente (ver Figura$\PageIndex{12}$). Incluya las unidades (segundos (s) y metros (m)).
Coloca tus parámetros WINDOW al final de cada eje (ver Figura$\PageIndex{12}$).
Etiquete la gráfica con su ecuación (ver Figura$\PageIndex{12}$).
Dibuja una línea vertical discontinua a través$t$ de la intersección. Sombra y etiquete el$t$ valor -del punto donde la línea vertical discontinua cruza el$t$ eje -eje. Esta es la solución de la ecuación$0 = 8 + 100t−4.9t^2$ (ver Figura$\PageIndex{12}$).

higo 5.3.12.png — Figura$\PageIndex{12}$: Reportando tu solución gráfica en tu tarea.

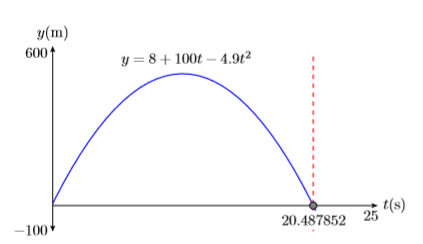
Redondeando a la décima de segundo más cercana, el proyectil tarda aproximadamente$t ≈ 20.5$ segundos en impactar contra el suelo.

Ejercicio$\PageIndex{4}$

Si se lanza un proyectil con una velocidad inicial de$60$ meters per second from a rooftop $12$ meters above ground level, at what time will the projectile return to ground level?

Responder: $\approx 12.441734$segundos

Search

Text Color

Text Size

Margin Size

Font Type