5.4: Sumando y restando polinomios

Última actualización
Guardar como PDF

Page ID: 111670

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En esta sección nos concentramos en sumar y restar expresiones polinómicas, a partir de trabajos anteriores combinando términos similares en Poderes Ascendente y Descendente. Comencemos con un ejemplo de adición.

Ejemplo$\PageIndex{1}$

Simplificar:\[\left(a^{2}+3 a b-b^{2}\right)+\left(4 a^{2}+11 a b-9 b^{2}\right) \nonumber \]

Solución

Utilice las propiedades conmutativas y asociativas para cambiar el orden y reagruparse. Después combina términos similares.

\[\begin{aligned}\left(a^{2}+3 a b-b^{2}\right) &+\left(4 a^{2}+11 a b-9 b^{2}\right) \\ &=\left(a^{2}+4 a^{2}\right)+(3 a b+11 a b)+\left(-b^{2}-9 b^{2}\right) \\ &=5 a^{2}+14 a b-10 b^{2} \end{aligned} \nonumber \]

Ejercicio$\PageIndex{1}$

Simplificar:$\left(3 s^{2}-2 s t+4 t^{2}\right)+\left(s^{2}+7 s t-5 t^{2}\right)$

Responder: $4 s^{2}+5 s t-t^{2}$

Combinemos algunas funciones polinómicas.

Ejemplo$\PageIndex{2}$

Dado$f(x)=3x^2−4x−8$ y$g(x)=x^2−11x+15$, simplificar$f(x)+g(x)$.

Solución

Primero, sustituir$f(x)$ y$g(x)$ con sus deﬁniciones. Asegúrese de rodear cada polinomio con paréntesis, porque se nos pide que agreguemos todo$f(x)$ a todos$g(x)$.

\[f(x)+g(x) = (3x^2 −4x−8) + (x^2 −11x + 15) \nonumber \]Ahora usa las propiedades conmutativas y asociativas para cambiar el orden y reagruparse. Combina términos similares.

\[\begin{array}{l}{=\left(3 x^{2}+x^{2}\right)+(-4 x-11 x)+(-8+15)} \\ {=4 x^{2}-15 x+7}\end{array} \nonumber \]

De ahí,$f(x)+g(x)=4x^2 −15x + 7$.

Ejercicio$\PageIndex{2}$

Giv es$f(x)=2x^2 +9x−5$ y$g(x)=−x^2 −4x + 3$, simplify $f(x)+g(x)$.

Responder: $x^{2}+5 x-2$

Si te sientes cómodo saltando uno o dos pasos, no es necesario anotar todos los pasos que se muestran en Ejemplos$\PageIndex{1}$ y$\PageIndex{2}$. Intentemos combinar mentalmente términos similares en el siguiente ejemplo.

Ejemplo$\PageIndex{3}$

Simplificar:\[\left(x^{3}-2 x^{2} y+3 x y^{2}+y^{3}\right)+\left(2 x^{3}-4 x^{2} y-8 x y^{2}+5 y^{3}\right) \nonumber \]

Solución

Si usamos la propiedad asociativa y conmutativa para reordenar y reagruparnos, luego combinamos términos similares, obtenemos el siguiente resultado.

\[\begin{aligned}\left(x^{3}-2 x^{2} y\right.&+3 x y^{2}+y^{3} )+\left(2 x^{3}-4 x^{2} y-8 x y^{2}+5 y^{3}\right) \\ &=\left(x^{3}+2 x^{3}\right)+\left(-2 x^{2} y-4 x^{2} y\right)+\left(3 x y^{2}-8 x y^{2}\right)+\left(y^{3}+5 y^{3}\right) \\ &=3 x^{3}-6 x^{2} y-5 x y^{2}+6 y^{3} \end{aligned} \nonumber \]

Sin embargo, si podemos combinar mentalmente términos similares, eliminando el paso medio, es mucho más eficiente escribir:

\[\begin{array}{l}{\left(x^{3}-2 x^{2} y+3 x y^{2}+y^{3}\right)+\left(2 x^{3}-4 x^{2} y-8 x y^{2}+5 y^{3}\right)} \\ {\quad \quad=3 x^{3}-6 x^{2} y-5 x y^{2}+6 y^{3}}\end{array} \nonumber \]

Ejercicio$\PageIndex{3}$

Simplificar:$\left(-5 a^{2} b+4 a b-3 a b^{2}\right)+\left(2 a^{2} b+7 a b-a b^{2}\right)$

Responder: $-3 a^{2} b+11 a b-4 a b^{2} d$

Negando un polinomio

Antes de intentar restar polinomios, abordemos primero cómo negar o “tomar lo contrario” de un polinomio. Primero recordemos que negar equivale a multiplicar por$−1$.

Negando

Si$a$ hay algún número, entonces

\[−a =(−1)a. \nonumber \]

Es decir, negar equivale a multiplicar por$−1$.

Podemos utilizar esta propiedad para simplificar$−(a + b)$. Primero, negar es idéntico a multiplicar por$−1$. Entonces podemos distribuir el$−1$.

\[\begin{aligned} -(a+b) &= (-1)(a+b) \quad \color {Red} \text { Negating is equivalent to multiplying by } -1 \\ &= (-1) a+(-1) b \quad \color {Red} \text { Distribute the }-1 . \\ &= -a+(-b) \quad \color {Red} \text { Simplify: }(-1) a=-a \text { and }(-1) b=-b \\ &= -a-b \quad \color {Red} \text { Subtraction means add the opposite. } \end{aligned} \nonumber \]

Así,$−(a + b)=−a −b$. Sin embargo, probablemente sea más sencillo señalar que el signo menos frente a los paréntesis simplemente cambió el signo de cada término dentro de los paréntesis.

Negando una suma

Al negar una suma de términos, el efecto del signo menos es cambiar cada término entre paréntesis al signo opuesto. \[−(a + b)=−a−b \nonumber \]

Veamos este principio en el siguiente ejemplo.

Ejemplo$\PageIndex{4}$

Simplificar:$-\left(-3 x^{2}+4 x-8\right)$

Solución

Primero, negar equivale a multiplicar por$−1$. Después distribuir el$−1$.

\[\begin{aligned} -&\left(-3 x^{2}+4 x-8\right) \\ &=(-1)\left(-3 x^{2}+4 x-8\right) \quad \color {Red} \text{Negating is equivalent to multiplying by } -1\\ &=(-1)\left(-3 x^{2}\right)+(-1)(4 x)-(-1)(8) \quad \color {Red} \text {Distribute the } -1 \\ &=3 x^{2}+(-4 x)-(-8) \quad \color {Red} \text {Simplify: } (-1)(-3 x^{2})=3 x^{2}, (-1)(4 x)=-4 x, \text {and} (-1)(8)=-8\\ &=3 x^{2}-4 x+8 \quad \color {Red} \text {Subtraction means add the opposite.} \end{aligned} \nonumber \]

Solución alternativa:

Como vimos anteriormente, un signo negativo frente a un paréntesis simplemente cambia el signo de cada término dentro de los paréntesis. Por lo que es mucho más eficiente escribir\[−(−3x^2 +4x−8) = 3x^2 −4x +8 \nonumber \] simplemente cambiando el signo de cada término dentro de los paréntesis.

Ejercicio$\PageIndex{4}$

Simplificar:$-\left(2 x^{2}-3 x+9\right)$

Responder: $-2 x^{2}+3 x-9$

Restar polinomios

Ahora que sabemos negar un polinomio (cambiar el signo de cada término del polinomio), estamos listos para restar polinomios.

Ejemplo$\PageIndex{5}$

Simplificar:$\left(y^{3}-3 y^{2} z+4 y z^{2}+z^{3}\right)-\left(2 y^{3}-8 y^{2} z+2 y z^{2}-8 z^{3}\right)$

Solución

Primero, distribuir el signo menos, cambiando el signo de cada término del segundo polinomio.

\[\left(y^{3}-3 y^{2} z+4 y z^{2}+z^{3}\right)-\left(2 y^{3}-8 y^{2} z+2 y z^{2}-8 z^{3}\right)=y^{3}-3 y^{2} z+4 y z^{2}+z^{3}-2 y^{3}+8 y^{2} z-2 y z^{2}+8 z^{3} \nonumber \]

Reagruparse, combinando términos similares. Puedes realizar este siguiente paso mentalmente si lo deseas.

\[\begin{array}{l}{=\left(y^{3}-2 y^{3}\right)+\left(-3 y^{2} z+8 y^{2} z\right)+\left(4 y z^{2}-2 y z^{2}\right)+\left(z^{3}+8 z^{3}\right)} \\ {=-y^{3}+5 y^{2} z+2 y z^{2}+9 z^{3}}\end{array} \nonumber \]

Ejercicio$\PageIndex{5}$

Simplificar:$\left(4 a^{2} b+2 a b-7 a b^{2}\right)-\left(2 a^{2} b-a b-5 a b^{2}\right)$

Responder: $2 a^{2} b+3 a b-2 a b^{2}$

Vamos a restar dos funciones polinómicas.

Ejemplo$\PageIndex{6}$

Dado$p(x)=−5x^3 +6 x − 9$ y$q(x)=6 x^2 − 7x − 11$, simplificar$p(x)−q(x)$.

Solución

Primero, sustituir$p(x)$ y$q(x)$ con sus deﬁniciones. Debido a que se nos pide restar todo$q(x)$ de todos$p(x)$, es fundamental rodear cada polinomio con paréntesis.

\[p(x)-q(x)=\left(-5 x^{3}+6 x-9\right)-\left(6 x^{2}-7 x-11\right) \nonumber \]

Distribuye el signo menos, cambiando el signo de cada término en el segundo polinomio, luego reagrupa y combina términos similares.

\[\begin{array}{l}{=-5 x^{3}+6 x-9-6 x^{2}+7 x+11} \\ {\color {Red} =-5 x^{3}-6 x^{2}+(6 x+7 x)+(-9+11)} \\ {=-5 x^{3}-6 x^{2}+13 x+2}\end{array} \nonumber \]

Sin embargo, después de distribuir el signo menos, si podemos combinar mentalmente términos similares, eliminando el paso medio, es mucho más eficiente escribir:

\[\begin{aligned} p(x)-q(x) &=\left(-5 x^{3}+6 x-9\right)-\left(6 x^{2}-7 x-11\right) \\ &=-5 x^{3}+6 x-9-6 x^{2}+7 x+11 \\ &=-5 x^{3}-6 x^{2}+13 x+2 \end{aligned} \nonumber \]

Ejercicio$\PageIndex{6}$

Dado$f(x)=3x^2 +9x−4$ y$g(x)=−5x2 +4x−6$, simplificar$f(x)−g(x)$.

Responder: $8 x^{2}+5 x+2$

Algunas aplicaciones

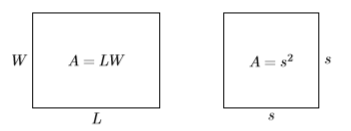
Recordemos que el área de un rectángulo que tiene longitud$L$ y anchura$W$ se encuentra usando la fórmula$A = LW$. El área de un cuadrado que tiene lado s se encuentra usando la fórmula$A = s^2$ (ver Figura$\PageIndex{1}$).

higo 5.4.1.png — Figura$\PageIndex{1}$: Fórmulas de área para el rectángulo y el cuadrado.

Ejemplo$\PageIndex{7}$

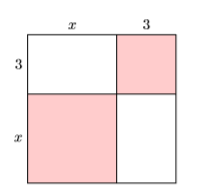
Encuentra el área del cuadrado en la Figura$\PageIndex{2}$ sumando el área de sus partes.

higo 5.4.2.png — Figura$\PageIndex{2}$: Encuentra la suma de las partes.

Solución

Separar cada una de las cuatro piezas y etiquetar cada una con su área (ver Figura$\PageIndex{3}$).

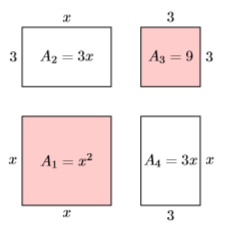
higo 5.4.3.png — Figura$\PageIndex{3}$: Encontrar el área de cada una de las cuatro partes.

Los dos cuadrados sombreados en la Figura$\PageIndex{3}$ tienen áreas$A_1 = x^2$ y$A_3 = 9$, respectivamente. Los dos rectángulos no sombreados en la Figura$\PageIndex{3}$ tienen áreas$A_2 =3 x$ y$A_4 =3x$. Sumar estas cuatro áreas nos da el área de toda la ﬁgura.

\[\begin{aligned} A &=A_{1}+A_{2}+A_{3}+A_{4} \\ &=x^{2}+3 x+9+3 x \\ &=x^{2}+6 x+9 \end{aligned} \nonumber \]

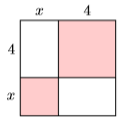
Ejercicio$\PageIndex{7}$

Encuentra el área del cuadrado que se muestra a continuación sumando el área de sus partes.

Responder: $x^{2}+8 x+16$

Ejemplo$\PageIndex{8}$

Ginger dirige un negocio de venta de canastas de mimbre. Sus costos de negocio para producir y vender cestas de$x$ mimbre vienen dados por la función polinómica$C(x)=100+3x−0.02x^2$. El ingreso que obtiene al vender canastas de$x$ mimbre viene dado por la función polinómica$R(x)=2.75x$. Encuentra una fórmula para$P(x)$, el proﬁt hecho a partir de la venta de cestas$x$ de mimbre. Usa tu fórmula para determinar el perfil de Ginger si vende canastas$123$ de mimbre.

Solución

El proﬁt hecho de la venta de cestas de$x$ mimbre se encuentra restando los costos incurridos de los ingresos recibidos. En símbolos:\[P(x)=R(x)−C(x) \nonumber \]
Siguiente, reemplace$R(x)$ y$C(x)$ con sus deﬁniciones. Debido a que se supone que debemos restar todo el costo de los ingresos, asegúrese de rodear el polinomio de costos con paréntesis. \[P(x)=2 .75x−(100 + 3x−0.02x^2) \nonumber \]
Distribuye el signo menos y combina términos similares.

\[\begin{array}{l}{=2.75 x-100-3 x+0.02 x^{2}} \\ {=0.02 x^{2}-0.25 x-100}\end{array} \nonumber \]

Así, la función proﬁt es$P(x)=0 .02x^2 −0.25x−100$.

A continuación, para determinar el proﬁt si se venden cestas de$123$ mimbre, sustituya$123$$x$ en la función proﬁt$P(x)$.

\[\begin{aligned} P(x) &=0.02 x^{2}-0.25 x-100 \\ P(123) &=0.02(123)^{2}-0.25(123)-100 \end{aligned} \nonumber \]

Ahora puedes usar tu calculadora gráfica para determinar el perfil (ver Figura$\PageIndex{5}$). De ahí que el proﬁt hecho a partir de la venta de canastas de$123$ mimbre es$\$171.83$.

higo 5.4.5.png — Figura$\PageIndex{5}$: Determinar el rendimiento de la venta de canastas$123$ de mimbre.

Ejercicio$\PageIndex{8}$

Los costos de producción y venta de$x$ widgets are given by the polynomial function $C(x) = 50 + 5x−0.5x^2$, and the revenue for selling $x$ widgets is given by the polynomial function $R(x)=3.5x$. Determine the proﬁt si$75$ widgets are sold.

Responder: $\$ 2,650$

Search

Text Color

Text Size

Margin Size

Font Type