5.5: Leyes de los Exponentes

En el capítulo 1, sección 1, introducimos primero la definición de exponente. Por conveniencia, repetimos esa definición.

En la expresión exponencial$a^n$, el número$a$ se llama la base, mientras que el número$n$ se llama exponente.

Exponentes

Dejar$a$ ser cualquier número real y dejar$n$ ser cualquier número entero. Si$n \neq 0$, entonces:

$$a^{n}=\underbrace{a \cdot a \cdot a \cdots \cdot a}_{n \text { times }} \nonumber$$

Es decir, para calcular$a^n$, escribir$a$ como factor$n$ tiempos. En el caso donde$a \neq 0$, pero$n = 0$, entonces definimos:

$$a^0 =1 \nonumber$$

Por ejemplo, elevar un número a la quinta potencia requiere que repitamos el número como factor cinco veces (ver Figura$\PageIndex{1}$).

$$\begin{aligned}(-2)^{5} &=(-2)(-2)(-2)(-2)(-2) \\ &=-32 \end{aligned} \nonumber$$

Figura$\PageIndex{1}$: Evaluación$(−2)^5$ y$(−1/2)^4$. Recordar: Utilice la tecla MATH para localizar el comando ► Frac.

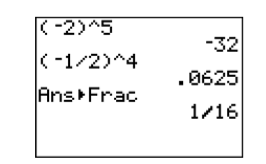
Elevar un número a la cuarta potencia requiere que repitamos ese número como factor cuatro veces (ver Figura$\PageIndex{1}$).

$$\begin{aligned}\left(-\dfrac{1}{2}\right)^{4} &=\left(-\dfrac{1}{2}\right)\left(-\dfrac{1}{2}\right)\left(-\dfrac{1}{2}\right)\left(-\dfrac{1}{2}\right) \\ &=\dfrac{1}{16} \end{aligned} \nonumber$$

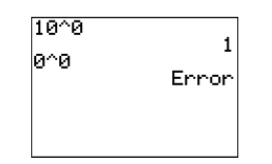
Como ejemplo final, tenga en cuenta que$10^0 = 1$, pero$0^0$ es indefinido (ver Figura$\PageIndex{2}$).

Figura$\PageIndex{2}$: Evaluación$10^0$ y$0^0$ sobre la calculadora gráfica.

Nota

Para aquellos que tal vez se estén preguntando por qué$a^0 = 1$, provided $a \neq 0$, aquí hay un buen argumento. Primero, tenga en cuenta que$a^1 = a$, so:

$$a \cdot a^{0}=a^{1} \cdot a^{0} \nonumber$$

A la derecha, repite la base y suma los exponentes.

$$a \cdot a^{0}=a^{1} \nonumber$$

O equivalentemente:

$$a \cdot a^{0}=a \nonumber$$

Ahora, divida ambos lados por$a$, which is permisible si$a \neq 0$.

$$\dfrac{a \cdot a^{0}}{a}=\dfrac{a}{a} \nonumber$$

Simplifique ambos lados:

$$a^0 =1 \nonumber$$

Multiplicar con bases similares

En la expresión$a^n$, el número$a$ se llama la base y el número$n$ se llama el exponente. Frecuentemente, se nos requerirá multiplicar dos expresiones exponenciales con bases similares, como$x^{3} \cdot x^{4}$. Recordemos que el exponente nos dice cuántas veces escribir cada base como factor, así podemos escribir:

$$\begin{aligned} x^{3} \cdot x^{4} &=(x \cdot x \cdot x) \cdot(x \cdot x \cdot x \cdot x) \\ &=x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \\ &=x^{7} \end{aligned} \nonumber$$

Tenga en cuenta que simplemente estamos contando el número de veces que$x$ ocurre como factor. Primero, tenemos tres$x’s$, luego cuatro$x’s$, para un total de siete$x’s$. Sin embargo un poco de pensamiento nos dice que es mucho más rápido simplemente sumar los exponentes para revelar el número total de veces que$x$ ocurre como factor.

$$\begin{aligned} x^{3} \cdot x^{4} &=x^{3+4} \\ &=x^{7} \end{aligned} \nonumber$$

La discusión anterior es un ejemplo de la siguiente ley general de exponentes.

Multiplicar con bases similares

Para multiplicar dos expresiones exponenciales con bases similares, repita la base y suma los exponentes.

$$a^{m} \cdot a^{n}=a^{m+n} \nonumber$$

Ejemplo$\PageIndex{1}$

Simplifica cada una de las siguientes expresiones:

1. $y^{4} \cdot y^{8}$
2. $2^{3} \cdot 2^{5}$
3. $(x+y)^{2}(x+y)^{7}$

Solución

En cada ejemplo tenemos como bases. Así, el enfoque será el mismo para cada ejemplo: repetir la base y sumar los exponentes.

1. $\begin{aligned} y^{4} \cdot y^{8} &=y^{4+8} \\ &=y^{12} \end{aligned}$
2. $\begin{aligned} 2^{3} \cdot 2^{5} &=2^{3+5} \\ &=2^{8} \end{aligned}$
3. $\begin{aligned}(x+y)^{2}(x+y)^{7} &=(x+y)^{2+7} \\ &=(x+y)^{9} \end{aligned}$

Con un poco de práctica, cada uno de los ejemplos se puede simplificar mentalmente. Repite la base y agrega los exponentes en tu cabeza:$y^{4} \cdot y^{8}=y^{12}, 2^{3} \cdot 2^{5}=2^{8}$ y$(x+y)^{2}(x+y)^{7}=(x+y)^{9}$.

Ejercicio$\PageIndex{1}$

$3^{4} \cdot 3^{2}$

Contestar

$3^6$

Ejemplo$\PageIndex{2}$

Simplificar:$\left(a^{6} b^{4}\right)\left(a^{3} b^{2}\right)$

Solución

Utilizaremos las propiedades conmutativas y asociativas para cambiar el orden de operación, luego repetimos las bases comunes y agregaremos los exponentes.

$$\begin{aligned} \left(a^{6} b^{4}\right)\left(a^{3} b^{2}\right) &= a^{6} b^{4} a^{3} b^{2} \quad \color {Red} \text { The associative property allows us to regroup in the order we prefer. } \\ &= a^{6} a^{3} b^{4} b^{2} \quad \color {Red} \text { The commutative property allows us to change the order of multiplication. } \\ &= a^{9} b^{6} \quad \color {Red} \text { Repeat the common bases and add the exponents. } \end{aligned} \nonumber$$

Con la práctica, nos damos cuenta de que si todos los operadores son multiplicación, entonces podemos multiplicar en el orden que preferimos, repitiendo las bases comunes y sumando mentalmente a los exponentes:$\left(a^{6} b^{4}\right)\left(a^{3} b^{2}\right)=a^{9} b^{6}$.

Ejercicio$\PageIndex{2}$

$\left(x^{2} y^{6}\right)\left(x^{4} y^{3}\right)$

Contestar

$x^{6} y^{9}$

Ejemplo$\PageIndex{3}$

Simplificar:$x^{n+3} \cdot x^{3-2 n}$

Solución

Nuevamente, repetimos la base y sumamos los exponentes.

$$\begin{aligned} x^{n+3} \cdot x^{3-2 n} &= x^{(n+3)+(3-2 n)} \quad \color {Red}\text { Repeat the base, add the exponents. } \\ &= x^{6-n} \quad \color {Red} \text { Simplify. Combine like terms. } \end{aligned} \nonumber$$

Ejercicio$\PageIndex{3}$

$x^{5-n} \cdot x^{4 n+2}$

Contestar

$x^{3 n+7}$

Dividir con bases similares

Al igual que la multiplicación, también se nos pedirá frecuentemente dividir expresiones exponenciales con bases similares, como$x^7/x^4$. Nuevamente, la clave es recordar que el exponente nos dice cuántas veces escribir la base como factor, para que podamos escribir:

$$\begin{aligned} \dfrac{x^{7}}{x^{4}} &= \dfrac{x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x}{x \cdot x \cdot x \cdot x} \\ &= \dfrac{\not {x} \cdot \not {x} \cdot \not{x} \cdot \not {x} \cdot x \cdot x \cdot x}{\not {x} \cdot \not {x} \cdot \not {x} \cdot \not {x}} \\ &= x^3 \end{aligned} \nonumber$$

Observe cómo cancelamos cuatro$x’s$ en el numerador por cuatro$x’s$ en el denominador. No obstante, en cierto sentido estamos “restando cuatro$x’s$” del numerador, por lo que una forma más rápida de proceder es repetir la base y restar los exponentes, de la siguiente manera:

$$\begin{aligned} \dfrac{x^{7}}{x^{4}} &=x^{7-4} \\ &=x^{3} \end{aligned} \nonumber$$

La discusión anterior es un ejemplo de la segunda ley general de exponentes.

Cómo dividir con bases similares

Para dividir dos expresiones exponenciales con bases similares, repita la base y resta los exponentes. Dado$a \neq 0$,

$$\dfrac{a^{m}}{a^{n}}=a^{m-n} \nonumber$$

Tenga en cuenta que la resta de los exponentes sigue la regla “arriba menos abajo”.

Nota

Aquí hay otro buen argumento por qué$a^0 = 1$, siempre y cuando$a \neq 0$. Comience con:

$$\dfrac{a^{1}}{a^{1}}=1 \nonumber$$

Repite la base y resta los exponentes.

$$a^{1-1}=1 \nonumber$$

Simplificar.

$$a^0 = 1 \nonumber$$

Ejemplo$\PageIndex{4}$

Simplifica cada una de las siguientes expresiones:

1. $\dfrac{x^{12}}{x^{3}}$
2. $\dfrac{5^{7}}{5^{7}}$
3. $\dfrac{(2 x+1)^{8}}{(2 x+1)^{3}}$

Solución

En cada ejemplo tenemos como bases. Así, el enfoque será el mismo para cada ejemplo: repetir la base y restar los exponentes.

1. $\begin{aligned} \dfrac{x^{12}}{x^{3}} &=x^{12-3} \\ &=x^{9} \end{aligned}$
2. $\begin{aligned} \dfrac{5^{7}}{5^{7}} &=5^{7-7} \\ &=5^{0} \\ &=1 \end{aligned}$
3. $\begin{aligned} \dfrac{(2 x+1)^{8}}{(2 x+1)^{3}} &=(2 x+1)^{8-3} \\ &=(2 x+1)^{5} \end{aligned}$

Con un poco de práctica, cada uno de los ejemplos se puede simplificar mentalmente. Repite la base y resta los exponentes en tu cabeza:$x^{12} / x^{3}=x^{9}, 5^{7} / 5^{4}=5^{3}$ y$(2 x+1)^{8} /(2 x+1)^{3}=(2 x+1)^{5}$.

Ejercicio$\PageIndex{4}$

$\dfrac{4^{5}}{4^{3}}$

Contestar

$4^2$

Ejemplo$\PageIndex{5}$

Simplificar:$\dfrac{12 x^{5} y^{7}}{4 x^{3} y^{2}}$

Solución

Primero expresamos la fracción como un producto de tres fracciones, las dos últimas con una base común. En la primera línea de la siguiente solución, tenga en cuenta que si multiplica numeradores y denominadores de las tres fracciones separadas, el producto equivale a la fracción original de la izquierda.

$$\begin{aligned} \dfrac{12 x^{5} y^{7}}{4 x^{3} y^{2}} &= \dfrac{12}{4} \cdot \dfrac{x^{5}}{x^{3}} \cdot \dfrac{y^{7}}{y^{2}} \quad \color {Red} \text { Break into a product of three fractions. } \\ &= 3 x^{5-3} y^{7-2} \quad \color {Red} \text { Simplify: } 12 / 4=3 . \text { Then repeat the common } \\ &= 3 x^{2} y^{5} \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber$$

Ejercicio$\PageIndex{5}$

Simplificar:$\dfrac{15 a^{6} b^{9}}{3 a b^{5}}$

Contestar

$5 a^{5} b^{4}$

Ejemplo$\PageIndex{6}$

Simplificar:$\dfrac{x^{5 n-4}}{x^{3-2 n}}$

Solución

Nuevamente, repetimos la base y restamos los exponentes.

$$\begin{aligned} \dfrac{x^{5 n-4}}{x^{3-2 n}} &= x^{(5 n-4)-(3-2 n)} \quad \color {Red} \text { Repeat the base, subtract exponents. } \\ &= x^{5 n-4-3+2 n} \quad \color {Red} \text { Distribute the minus sign. } \\ &= x^{7 n-7} \quad \color {Red} \text { Simplify. Combine like terms. } \end{aligned} \nonumber$$

Ejercicio$\PageIndex{6}$

Simplificar:$\dfrac{x^{3 n-6}}{x^{n+2}}$

Contestar

$x^{2 n-8}$

Elevar un Poder a un Poder

Supongamos que tenemos una expresión exponencial elevada a un segundo poder, como$(x^2)3$. El segundo exponente nos dice que$x^2$ escribamos como factor tres veces:

$$\begin{aligned} \left(x^{2}\right)^{3} &= x^{2} \cdot x^{2} \cdot x^{2} \quad \color {Red} \text { Write } x^{2} \text { as a factor three times. } \\ &= x^{6} \quad \color {Red} \text { Repeat the base, add the exponents. } \end{aligned} \nonumber$$

Tenga en cuenta cómo agregamos$2 + 2 + 2$ para obtener$6$. No obstante, una forma mucho más rápida de sumar “tres dos” es multiplicar:$3 \cdot 2=6$. Así, al elevar una “potencia a una segunda potencia”, repita la base y multiplica los exponentes, de la siguiente manera:

$$\begin{aligned}\left(x^{2}\right)^{3} &=x^{2 \cdot 3} \\ &=x^{6} \end{aligned} \nonumber$$

La discusión anterior da lugar a la siguiente tercera ley de exponentes.

Elevar un Poder a un Poder

Al elevar una potencia a una potencia, repite la base y multiplica los exponentes. En símbolos:
$$(a^m)^n = a^{mn} \nonumber$$
Tenga en cuenta que yuxtaponer dos variables, como en$mn$, significa “$m$tiempos”$n$.

Ejemplo$\PageIndex{7}$

Simplifica cada una de las siguientes expresiones:

1. $\left(z^{3}\right)^{5}$
2. $\left(7^{3}\right)^{0}$
3. $\left[(x-y)^{3}\right]^{6}$

Solución

En cada ejemplo estamos elevando un poder a un poder. De ahí que en cada caso, repetimos la base y multiplicamos los exponentes.

1. $\begin{aligned}\left(z^{3}\right)^{5} &=z^{3.5} \\ &=z^{15} \end{aligned}$
2. $\begin{aligned}\left(7^{3}\right)^{0} &=7^{3.0} \\ &=7^{0} \\ &=1 \end{aligned}$
3. $\begin{aligned}\left[(x-y)^{3}\right]^{6} &=(x-y)^{3 \cdot 6} \\ &=(x-y)^{18} \end{aligned}$

Con un poco de práctica, cada uno de los ejemplos se puede simplificar mentalmente. Repite la base y multiplica los exponentes en tu cabeza:$\left(z^{3}\right)^{5}=z^{15},\left(7^{3}\right)^{4}=7^{12}$ y$\left[(x-y)^{3}\right]^{6}=(x-y)^{18}$.

Ejercicio$\PageIndex{7}$

Simplificar:$\left(2^{3}\right)^{4}$

Contestar

$2^{12}$

Ejemplo$\PageIndex{8}$

Simplificar:$\left(x^{2 n-3}\right)^{4}$

Solución

Nuevamente, repetimos la base y multiplicamos los exponentes.

$$\begin{aligned} \left(x^{2 n-3}\right)^{4} &= x^{4(2 n-3)} \quad \color {Red} \text { Repeat the base, multiply exponents. } \\ &= x^{8 n-12} \quad \color {Red} \text { Distribute the } 4 . \end{aligned} \nonumber$$

Ejercicio$\PageIndex{8}$

Simplificar:$\left(a^{2-n}\right)^{3}$

Contestar

$a^{6-3 n}$

Elevar un producto a una potencia

Con frecuencia tenemos necesidad de elevar un producto a una potencia, como$(xy)^3$. Nuevamente, recuerden que el exponente nos está diciendo que escribamos$xy$ como factor tres veces, así:

$$\begin{aligned} (x y)^{3} &=(x y)(x y)(x y) \quad \color {Red} \text {Write } xy \text { as a factor three times.}\\ &=x y x y x y \quad \color {Red} \text {The associative property allows us to group as we please.}\\ &=x x x y y y \quad \color {Red} \text {The commutative property allows us to change the order as we please.}\\ &=x^{3} y^{3} \quad \color {Red} \text {Invoke the exponent definition: } x x x=x^{3} \text { and } y y y=y^{3} \end{aligned} \nonumber$$

No obstante, es mucho más sencillo señalar que cuando elevas un producto a una potencia, elevas cada factor a esa potencia. En símbolos: $$(xy)^3 = x^3y^3 \nonumber$$
La discusión precedente nos lleva a una cuarta ley de exponentes.

Elevar un producto a una potencia

Para elevar un producto a una potencia, elevar cada factor a esa potencia. En símbolos:

$$(ab)^n = a^nb^n \nonumber$$

Ejemplo$\PageIndex{9}$

Simplifica cada una de las siguientes expresiones:

1. $(y z)^{5}$
2. $(-2 x)^{3}$
3. $(-3 y)^{2}$

Solución

En cada ejemplo estamos elevando un producto a una potencia. De ahí que en cada caso, elevemos cada factor a esa potencia.

1. $(y z)^{5}=y^{5} z^{5}$
2. $\begin{aligned}(-2 x)^{3} &=(-2)^{3} x^{3} \\ &=-8 x^{3} \end{aligned}$
3. $\begin{aligned}(-3 y)^{2} &=(-3)^{2} y^{2} \\ &=9 y^{2} \end{aligned}$

Con un poco de práctica, cada uno de los ejemplos se puede simplificar mentalmente. Levanta cada factor a la potencia indicada en tu cabeza:$(y z)^{5}=y^{5} z^{5},(-2 x)^{3}=-8 x^{3}$ y$(-3 y)^{2}=9 y^{2}$

Ejercicio$\PageIndex{9}$

Simplificar:$(-2 b)^{4}$

Contestar

$16 b^{4}$

Al elevar un producto de tres factores a una potencia, es fácil demostrar que debemos elevar cada factor a la potencia indicada. Por ejemplo,$(a b c)^{3}=a^{3} b^{3} c^{3}$. En general, esto es cierto independientemente del número de factores. Al elevar un producto a una potencia, elevar cada uno de los factores a la potencia indicada.

Ejemplo$\PageIndex{10}$

Simplificar:$\left(-2 a^{3} b^{2}\right)^{3}$

Solución

Elevar cada factor a la tercera potencia, luego simplificar.

$$\begin{aligned} \left(-2 a^{3} b^{2}\right)^{3} &= (-2)^{3}\left(a^{3}\right)^{3}\left(b^{2}\right)^{3} \quad \color {Red} \text { Raise each factor to the third power. } \\ &= -8 a^{9} b^{6} \quad \color {Red} \text {Simplify: } (-2)^{3}=8 \text {. In the remaining factors, raising a power to a power requires that we multiply the exponents. } \end{aligned} \nonumber$$

Ejercicio$\PageIndex{10}$

Simplificar:$\left(-3 x y^{4}\right)^{5}$

Contestar

$-243 x^{5} y^{20}$

Ejemplo$\PageIndex{11}$

Simplificar:$\left(-2 x^{2} y\right)^{2}\left(-3 x^{3} y\right)$

Solución

En el primer producto agrupado, elevar cada factor a la segunda potencia.

$$\begin{aligned} \left(-2 x^{2} y\right)^{2}\left(-3 x^{3} y\right) &=\left((-2)^{2}\left(x^{2}\right)^{2} y^{2}\right)\left(-3 x^{3} y\right) \quad \color {Red} \text { Raise each factor in the first grouped product to the second power.} \\ &=\left(4 x^{4} y^{2}\right)\left(-3 x^{3} y\right) \quad \color {Red} \text { Simplify: } (-2)^{2}=4 \text { and } \left(x^{2}\right)^{2}=x^{4} \end{aligned} \nonumber$$

La propiedad asociativa y conmutativa nos permite multiplicar los seis factores en el orden que nos plazca. De ahí, vamos a multiplicar$4$ y$−3$, entonces$x^4$ y$x^3$, y\ (y^2 e y, en ese orden. En este caso, repetimos la base y sumamos los exponentes.

$$\begin{aligned} &=-12x^7y^3 \quad \color {Red} \text { Simplify: } (4)(-3)=-12. \text { Also, } x^{4}x^3=x^{7} \text { and } y^2y = y^3\end{aligned} \nonumber$$

Ejercicio$\PageIndex{11}$

Simplificar:$\left(-a^{3} b^{2}\right)^{3}\left(-2 a^{2} b^{4}\right)^{2}$

Contestar

$-4 a^{13} b^{14}$

Elevar un cociente a un poder

Elevar un cociente a una potencia es similar a elevar un producto a una potencia. Por ejemplo, elevar$(x/y)^3$ requiere que escribamos$x/y$ como factor tres veces.

$$\begin{aligned}\left(\frac{x}{y}\right)^{3} &=\frac{x}{y} \cdot \frac{x}{y} \cdot \frac{x}{y} \\ &=\frac{x \cdot x \cdot x}{y \cdot y \cdot y} \\ &=\frac{x^{3}}{y^{3}} \end{aligned} \nonumber$$

No obstante, es mucho más sencillo darse cuenta de que cuando elevas un cociente a una potencia, elevas tanto el numerador como el denominador a ese poder. En símbolos:

$$\left(\dfrac{x}{y}\right)^{3}=\frac{x^{3}}{y^{3}} \nonumber$$

Esto lleva a la quinta y última ley de exponentes.

Elevar un cociente a un poder

Para elevar un cociente a un poder, elevar tanto el numerador como el denominador a ese poder. Dado$b \neq 0$,

$$\left(\dfrac{a}{b}\right)^{n}=\dfrac{a^{n}}{b^{n}} \nonumber$$

Ejemplo$\PageIndex{12}$

Simplifica cada una de las siguientes expresiones:

1. $\left(\dfrac{2}{3}\right)^{2}$
2. $\left(\dfrac{x}{3}\right)^{3}$
3. $\left(-\dfrac{2}{y}\right)^{4}$

Solución

En cada ejemplo estamos elevando un cociente a una potencia. De ahí que en cada caso, elevemos tanto el numerador como el denominador a esa potencia.

1. $\begin{aligned}\left(\dfrac{2}{3}\right)^{2} &=\dfrac{2^{2}}{3^{2}} \\ &=\dfrac{4}{9} \end{aligned}$
2. $\begin{aligned}\left(\dfrac{x}{3}\right)^{3} &=\dfrac{x^{3}}{3^{3}} \\ &=\dfrac{x^{3}}{27} \end{aligned}$
3. $\begin{aligned}\left(-\dfrac{2}{y}\right)^{4} &=\dfrac{2^{4}}{y^{4}} \\ &=\dfrac{16}{y^{4}} \end{aligned}$

Obsérvese que en el ejemplo (c), elevar una base negativa a una potencia par produce un resultado positivo. Con un poco de práctica, cada uno de los ejemplos se puede simplificar mentalmente. Levanta el numerador y denominador a la potencia indicada en tu cabeza:$(2 / 3)^{2}=4 / 9,(x / 3)^{3}=x^{3} / 27,$ y$(-2 / y)^{4}=16 / y^{4}$

Ejercicio$\PageIndex{12}$

Simplificar:$\left(\dfrac{5}{4}\right)^{3}$

Contestar

$\dfrac{125}{64}$

Ejemplo$\PageIndex{13}$

Simplificar:$\left(\dfrac{2 x^{5}}{y^{3}}\right)^{2}$

Solución

Levante tanto el numerador como el denominador a la segunda potencia, luego simplifique:

$$\begin{aligned} \left(\dfrac{2 x^{5}}{y^{3}}\right)^{2}=\dfrac{\left(2 x^{5}\right)^{2}}{\left(y^{3}\right)^{2}} \quad \color {Red} \text {Raise numerator and denominator to the second power.} \end{aligned} \nonumber$$

En el numerador, necesitamos elevar cada factor del producto a la segunda potencia. Entonces tenemos que recordarnos que cuando elevamos una potencia a una potencia, multiplicamos los exponentes.

$$\begin{aligned} &= \dfrac{2^{2}\left(x^{5}\right)^{2}}{\left(y^{3}\right)^{2}} \quad \color {Red} \text {Raise each factor in the numerator and denominator to the second power.} \\ &= \dfrac{4 x^{10}}{y^{6}} \quad \color {Red} \text { Simplify: } 2^{2}=4,\left(x^{5}\right)^{2}=x^{10} \text {, and } (y^3)^2=y^6 \end{aligned} \nonumber$$

Ejercicio$\PageIndex{13}$

Simplificar:$\left(\dfrac{a^{4}}{3 b^{2}}\right)^{3}$

Contestar

$\dfrac{a^{12}}{27 b^{6}}$