6.1: El mayor factor común

Comenzamos esta sección con definiciones de factores y divisores. Porque$24 = 2\cdot 12$, ambos$2$ y$12$ son factores de$24$. No obstante, tenga en cuenta que también$2$ es un divisor de$24$, porque cuando se divide$24$ por se$2$ obtiene$12$, con un resto de cero. De igual manera, también$12$ es un divisor de$24$, porque cuando se divide$24$ por se$12$ obtiene$2$, con un resto de cero.

Definiciones: Factores y divisores

Supongamos$m$ y$n$ son enteros. Entonces$m$ es un divisor (factor) de$n$ si y sólo si existe otro entero$k$ así que eso$n=m \cdot k$.

Las palabras divisor y factor son equivalentes. Tienen el mismo significado.

Ejemplo$\PageIndex{1}$

Enumerar los divisores positivos (factores) de$24$.

Solución

Primero, enumere todas las formas posibles que podemos expresar$24$ como producto de dos enteros positivos:

$$24=1 \cdot 24 \quad \text { or } \quad 24=2 \cdot 12 \quad \text { or } \quad 24=3 \cdot 8 \quad \text { or } \quad 24=4 \cdot 6 \nonumber$$

Por lo tanto, los divisores positivos (factores) de$24$ son$1,2,3,4,6,8,$ y$24$.

Ejercicio$\PageIndex{1}$

Enumere los divisores positivos de$18$.

Responder

$1,2,3,6,9,$y$18$

Ejemplo$\PageIndex{2}$

Enumere los divisores positivos (factores) que$36$ y$48$ tienen en común.

Solución

Primero, enumere todos los divisores positivos (factores) de$36$ y$48$ por separado, luego recubra los divisores que están en común.

Los divisores de$36$ son:$[1],[2],[3],[4],[6], 9, [12], 18, 36$

Los divisores de$48$ son:$[1],[2],[3],[4],[6], 8, [12], 16, 24, 48$

Por lo tanto, los divisores (factores) positivos comunes de$36$ y$48$ son$1, 2, 3, 4, 6,$ y$12$.

Ejercicio$\PageIndex{2}$

Enumere los divisores positivos que$40$ y$60$ tienen en común.

Responder

$1,2,4,5,10,$y$20$

Definición: Divisor común más grande

El mayor divisor común (factor) de$a$ y$b$ es el mayor número positivo que divide uniformemente (sin resto) ambos$a$ y$b$. El mayor divisor común de$a$ y$b$ se denota por el simbolismo$\operatorname{GCD}(a, b)$. También usaremos la abreviatura$\operatorname{GCF}(a, b)$ para representar el mayor factor común de$a$ y$b$.

Recuerde, el mayor divisor común y el mayor factor común tienen el mismo significado. En Ejemplo$\PageIndex{2}$, enumeramos los divisores positivos comunes de$36$ y$48$. El más grande de estos divisores comunes fue$12$. De ahí que el mayor común divisor (factor) de$36$ y$48$ es$12$, escrito$\operatorname{GCD}(36, 48)=12$.

Con números más pequeños, suele ser fácil identificar el divisor (factor) más común.

Ejemplo$\PageIndex{3}$

Indicar el mayor común divisor (factor) de cada uno de los siguientes pares de números:

1. $18$y$24$
2. $30$y$40$
3. $16$y$24$

Solución

En cada caso, debemos encontrar el mayor número entero positivo posible que divida uniformemente en ambos números dados.

1. El entero positivo más grande que se divide uniformemente en ambos$18$ y$24$ es$6$. Por lo tanto,$\operatorname{GCD}(18, 24)=6$.
2. El entero positivo más grande que se divide uniformemente en ambos$30$ y$40$ es$10$. Así,$\operatorname{GCD}(30, 40)=10$.
3. El entero positivo más grande que se divide uniformemente en ambos$16$ y$24$ es$8$. Así,$\operatorname{GCD}(16, 24)=8$.

Ejercicio$\PageIndex{3}$

Estado el mayor divisor común de$36$ y$60$.

Responder

$12$

Con números más grandes, es más difícil identificar el mayor divisor (factor) común. Sin embargo, ¡la factorización prime salvará el día!

Ejemplo$\PageIndex{4}$

Encuentra el divisor (factor) más común de$360$ y$756$.

Solución

Factor prime$360$ y$756$, escribiendo tu respuesta en forma exponencial.

Figura$\PageIndex{1}$

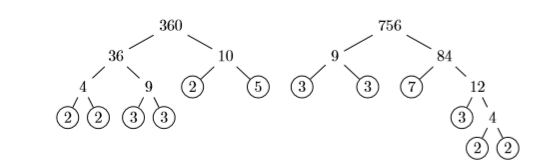
Por lo tanto:

$$\begin{array}{l}{360=2^{3} \cdot 3^{2} \cdot 5} \\ {756=2^{2} \cdot 3^{3} \cdot 7}\end{array} \nonumber$$

Nota

Para encontrar el mayor divisor (factor) común, enumere cada factor que aparece en común a la potencia más alta que aparece en común.

En este caso, los factores$2$ y$3$ aparecen en común,$22$ siendo el mayor poder$2$ y$32$ siendo el poder más elevado de los$3$ que aparecen en común. Por lo tanto, el mayor divisor común de$360$ y$756$ es:

$$\begin{aligned} \mathrm{GCD}(360,756) &=2^{2} \cdot 3^{2} \\ &=4 \cdot 9 \\ &=36 \end{aligned} \nonumber$$

Por lo tanto, el mayor divisor (factor) común es$\mathrm{GCD}(360,756)=36$. Tenga en cuenta lo que sucede cuando escribimos cada uno de los números dados como producto del mayor factor común y un segundo factor:

$$\begin{array}{l}{360={\color {Red} 36} \cdot 10} \\ {756={\color {Red} 36} \cdot 21}\end{array} \nonumber$$

En cada caso, observe cómo el segundo segundo factor ($10$y$21$) no contiene factores comunes adicionales.

Ejercicio$\PageIndex{4}$

Encuentra el mayor divisor común de$120$ y$450$.

Responder

$30$

Encontrar el mayor factor común de los monomios

El ejemplo$\PageIndex{4}$ revela la técnica utilizada para encontrar el mayor factor común de dos o más monomios.

Encontrar el GCF de dos o más monomios

Para encontrar el mayor factor común de dos o más monomios, proceda de la siguiente manera:

1. Encuentra el factor común (divisor) más grande de los coedecientes de los monomios dados. Utilice factorización prima si es necesario.
2. Enumere cada variable que aparece en común en los monomios dados.
3. Elevar cada variable que aparece en común a la potencia más alta que aparece en común entre los monomios dados.

Ejemplo$\PageIndex{5}$

Encuentra el mayor factor común de$6 x^{3} y^{3}$ y$9 x^{2} y^{5}$.

Solución

Para encontrar el$\mathrm{GCF}$ de$6 x^{3} y^{3}$ y$9 x^{2} y^{5}$, observamos que:

1. El mayor factor común (divisor) de$6$ y$9$ es$3$.
2. Los monomios$6x^3y^3$ y$9x^2y^5$ tienen las variables$x$ y$y$ en común.
3. El poder más alto de$x$ en común es$x^2$. El poder más alto de$y$ en común es$y^3$.

Así, el mayor factor común es$\mathrm{GCF}\left(6 x^{3} y^{3}, 9 x^{2} y^{5}\right)=3 x^{2} y^{3}$. Tenga en cuenta lo que sucede cuando escribimos cada uno de los monomios dados como producto del mayor factor común y un segundo monomio:

$$\begin{array}{l}{6 x^{3} y^{3}={\color {Red} 3 x^{2} y^{3}} \cdot 2 x} \\ {9 x^{2} y^{5}={\color {Red} 3 x^{2} y^{3}} \cdot 3 y}\end{array} \nonumber$$

Observe que el conjunto de factores del segundo monomio ($2x$y$3y$) no contiene factores comunes adicionales.

Ejercicio$\PageIndex{5}$

Encuentra el mayor factor común de$16xy^3$ y$12x^4y^2$.

Responder

$4 x y^{2}$

Ejemplo$\PageIndex{6}$

Encuentra el mayor factor común de$12x^4$,$18 x^3$, y$30 x^2$.

Solución

Para encontrar el$\mathrm{GCF}$ de$12x^4$,$18 x^3$, y$30 x^2$, observamos que:

1. El mayor factor común (divisor) de$12$,$18$, y$30$ es$6$.
2. Los monomios$12x^4$,$18 x^3$, y$30 x^2$ tienen la variable$x$ en común.
3. El poder más alto de$x$ en común es$x^2$.

Así, el mayor factor común es$\mathrm{GCF}\left(12 x^{4}, 18 x^{3}, 30 x^{2}\right)=6 x^{2}$. Tenga en cuenta lo que sucede cuando escribimos cada uno de los monomios dados como producto del mayor factor común y un segundo monomio:

$$\begin{array}{l}{12 x^{4}={\color {Red}6 x^{2}} \cdot 2 x^{2}} \\ {18 x^{3}={\color {Red}6 x^{2}} \cdot 3 x} \\ {30 x^{2}={\color {Red}6 x^{2}} \cdot 5}\end{array} \nonumber$$

Observe que el conjunto de factores del segundo monomio ($2x^2$,$3 x$, y$5$) no contiene factores comunes adicionales.

Ejercicio$\PageIndex{6}$

Encuentra el mayor factor común de$6y^3$,$15 y^2$, y$9 y^5$.

Responder

$3 y^{2}$

Factorizar el GCF

En el Capítulo 5, multiplicamos un monomio y un polinomio distribuyendo los tiempos monomiales de cada término en el polinomio.

$$\begin{aligned} {\color {Red}2 x(}3 x^{2}+4 x-7{\color {Red})} &={\color {Red}2 x} \cdot 3 x^{2}+{\color {Red}2 x} \cdot 4 x-{\color {Red}2 x} \cdot 7 \\ &=6 x^{3}+8 x^{2}-14 x \end{aligned} \nonumber$$

En esta sección invertimos ese proceso de multiplicación. Te presentamos el producto final y te pedimos que recuperes el problema de multiplicación original. En el caso$6 x^{3}+8 x^{2}-14 x$, el mayor factor común de$6x^3$,$8x^2$, y$14x$ es$2x$. Luego usamos la propiedad distributiva para factorizar$2x$ de cada término del polinomio.

$$\begin{aligned} 6 x^{3}+8 x^{2}-14 x &={\color {Red}2 x} \cdot 3 x^{2}+{\color {Red}2 x} \cdot 4 x-{\color {Red}2 x} \cdot 7 \\ &={\color {Red}2 x(}3 x^{2}+4 x-7{\color {Red})} \end{aligned} \nonumber$$

Factoring

El factoraje es “no multiplicar”. Se le da el producto, luego se le pide que encuentre el problema de multiplicación original.

Primera regla de factorización

Si los términos del polinomio dado tienen un mayor factor común ($\mathrm{GCF}$), entonces factorizar el$\mathrm{GCF}$.

Veamos algunos ejemplos que factorizan el$\mathrm{GCF}$.

Ejemplo$\PageIndex{7}$

Factor:$6 x^{2}+10 x+14$

Solución

El mayor factor común ($\mathrm{GCF}$) de$6x^2$,$10 x$ y$14$ es$2$. Factorizar el$\mathrm{GCF}$.

$$\begin{aligned} 6 x^{2}+10x+14 x &={\color {Red}2 } \cdot 3 x^{2}+{\color {Red}2 } \cdot 5 x+{\color {Red}2 } \cdot 7 \\ &={\color {Red}2 (}3 x^{2}+5 x+7{\color {Red})} \end{aligned} \nonumber$$

Comprobando tu trabajo

Cada vez que factorizas un polinomio, vuelve a multiplicar para verificar tu trabajo.

Comprobar: Multiplicar. Distribuir el$2$.

$$\begin{aligned} {\color {Red}2 (}3 x^{2}+5 x+7{\color {Red})} &={\color {Red}2 } \cdot 3 x^{2}+{\color {Red}2 } \cdot 5 x+{\color {Red}2 } \cdot 7 \\ &=6 x^{2}+10 x+14 \end{aligned} \nonumber$$

Ese es el polinomio original, así que factorizamos correctamente.

Ejercicio$\PageIndex{7}$

Factor:$9 y^{2}-15 y+12$

Responder

$3\left(3 y^{2}-5 y+4\right)$

Ejemplo$\PageIndex{8}$

Factor:$12 y^{5}-32 y^{4}+8 y^{2}$

Solución

El mayor factor común ($\mathrm{GCF}$) de$12y^5$,$32y^4$ y$8y^2$ es$4y^2$. Factorizar el$\mathrm{GCF}$.

$$\begin{aligned} 12 y^{5}-32 y^{4}+8 y^{2} &={\color {Red}4 y^{2}} \cdot 3 y^{3}-{\color {Red}4 y^{2}} \cdot 8 y^{2}+{\color {Red}4 y^{2}} \cdot 2 \\ &={\color {Red}4 y^{2} (}3 y^{3}-8 y^{2}+2{\color {Red})} \end{aligned} \nonumber$$

Comprobar: Multiplicar. Distribuir el monomio$4y^2$.

$$\begin{aligned} {\color {Red}4 y^{2} (}3 y^{3}-8 y^{2}+2{\color {Red})} &={\color {Red}4 y^{2}} \cdot 3 y^{3}-{\color {Red}4 y^{2}} \cdot 8 y^{2}+{\color {Red}4 y^{2}} \cdot 2 \\ &=12 y^{5}-32 y^{4}+8 y^{2} \end{aligned} \nonumber$$

Ese es el polinomio original. Hemos factorizado correctamente.

Ejercicio$\PageIndex{8}$

Factor:$8 x^{6}+20 x^{4}-24 x^{3}$

Responder

$4 x^{3}\left(2 x^{3}+5 x-6\right)$

Ejemplo$\PageIndex{9}$

Factor:$12 a^{3} b+24 a^{2} b^{2}+12 a b^{3}$

Solución

El mayor factor común ($\mathrm{GCF}$) de$12a^3b$,$24 a^2b^2$ y$12ab^3$ es$12ab$. Factorizar el$\mathrm{GCF}$.

$$\begin{aligned} 12 a^{3} b+24 a^{2} b^{2}+12 a b^{3} &={\color {Red}12ab} \cdot a^{2}-{\color {Red}12ab} \cdot 2 a b+{\color {Red}12ab} \cdot b^{2} \\ &= {\color {Red}12ab (}a^{2}+2ab+b^{2}{\color {Red})} \end{aligned} \nonumber$$

Comprobar: Multiplicar. Distribuir el monomio$12ab$.

$$\begin{aligned} {\color {Red}12ab (}a^{2}+2ab+b^{2}{\color {Red})} &={\color {Red}12ab} \cdot a^{2}-{\color {Red}12ab} \cdot 2 a b+{\color {Red}12ab} \cdot b^{2} \\ &=12 a^{3} b+24 a^{2} b^{2}+12 a b^{3} \end{aligned} \nonumber$$

Ese es el polinomio original. Hemos factorizado correctamente.

Ejercicio$\PageIndex{9}$

Factor:$15 s^{2} t^{4}+6 s^{3} t^{2}+9 s^{2} t^{2}$

Responder

$3 s^{2} t^{2}\left(5 t^{2}+2 s+3\right)$

Acelerar un poco las cosas

Eventualmente, después de mostrar tu trabajo en una serie de ejemplos$\PageIndex{7}$ como los de Ejemplos$\PageIndex{9}$,, y, necesitarás aprender a realizar el proceso mentalmente.$\PageIndex{8}$

Ejemplo$\PageIndex{10}$

Factorizar cada uno de los siguientes polinomios:

1. $24 x+32$
2. $5 x^{3}-10 x^{2}-10 x$
3. $2 x^{4} y+2 x^{3} y^{2}-6 x^{2} y^{3}$

Solución

En cada caso, factorizar el mayor factor común ($\mathrm{GCF}$):

1. El$\mathrm{GCF}$ de$24x$ y$32$ es$8$. Por lo tanto, $$24x + 32 = 8(3x + 4) \nonumber$$
2. El$\mathrm{GCF}$ de$5x^3$,$10 x^2$, y$10 x$ es$5x$. Por lo tanto: $$5 x^{3}-10 x^{2}-10 x=5 x\left(x^{2}-2 x-2\right) \nonumber$$
3. El$\mathrm{GCF}$ de$2x^4y$,$2x^3y^2$, y$6x^2y^3$ es$2x^2y$. Por lo tanto: $$2 x^{4} y+2 x^{3} y^{2}-6 x^{2} y^{3}=2 x^{2} y\left(x^{2}+x y-3 y^{2}\right) \nonumber$$

A medida que aceleras las cosas factorizando mentalmente el\(\mathrm{GCF}\), es aún más importante que revises tus resultados. El chequeo también se puede hacer mentalmente. Por ejemplo, al verificar el tercer resultado, distribuir mentalmente$2x^2y$ veces cada término de$x^2 +xy−3y^2$. Multiplicando$2x^2y$ veces el primer término$x^2$ produce$2x^4y$, el primer término en el polinomio original.

Continuar de esta manera, comprobando mentalmente el producto de$2x^2y$ con cada término de$x^2 + xy −3y^2$, asegurándose que cada resultado concuerda con el término correspondiente del polinomio original.

Ejercicio$\PageIndex{10}$

Factor:$18 p^{5} q^{4}-30 p^{4} q^{5}+42 p^{3} q^{6}$

Responder

$6 p^{3} q^{4}\left(3 p^{2}-5 p q+7 q^{2}\right)$

Recuerda que la propiedad distributiva nos permite$\mathrm{GCF}$ sacar la salida frente a la expresión o sacarla atrás. En símbolos:

${\color {Red}a}b+{\color {Red}a}c={\color {Red}a}(b+c) \quad$o$\quad b{\color {Red}a}+c{\color {Red}a}=(b+c){\color {Red}a}$

Ejemplo$\PageIndex{11}$

Factor:$2 x(3 x+2)+5(3 x+2)$

Solución

En este caso, el mayor factor común ($\mathrm{GCF}$) es$3x + 2$.

$$\begin{aligned} 2x(3 x+2)+5(3 x+2) &=2x \cdot {\color {Red}(3 x+2)}+5 \cdot{\color {Red}(3 x+2)} \\ &=(2 x+5){\color {Red}(3 x+2)} \end{aligned} \nonumber$$

Debido a la propiedad conmutativa de la multiplicación, es igualmente válido$\mathrm{GCF}$ sacar al frente.

$$\begin{aligned} 2x(3 x+2)+5(3 x+2) &=2x \cdot {\color {Red}(3 x+2)}+5 \cdot{\color {Red}(3 x+2)} \\ &={\color {Red}(3 x+2)} (2 x+5)\end{aligned}$$

Obsérvese que el orden de los factores difiere de la primera solución, pero debido a la propiedad conmutativa de la multiplicación, el orden no importa. Las respuestas son las mismas.

Ejercicio$\PageIndex{11}$

Factor:$3 x^{2}(4 x-7)+8(4 x-7)$

Responder

$\left(3 x^{2}+8\right)(4 x-7)$

Ejemplo$\PageIndex{12}$

Factor:$15 a(a+b)-12(a+b)$

Solución

En este caso, el mayor factor común ($\mathrm{GCF}$) es$3(a + b)$.

$$\begin{aligned} 15 a(a+b)-12(a+b) &={\color {Red}3(a+b)} \cdot 5 a-{\color {Red}3(a+b)} \cdot 4 \\ &={\color {Red}3(a+b)}(5 a-4) \end{aligned} \nonumber$$

Solución alternativa:

Es posible que no te des cuenta de eso$15$ y$12$ sean divisibles por$3$, factorizando solo el factor común$a + b$.

$$\begin{aligned} 15 a(a+b)-12(a+b) &=15a\cdot {\color {Red}(a+b)} - 12\cdot {\color {Red}(a+b)} \\ &=(15a-12) {\color {Red}(a+b)}\end{aligned} \nonumber$$

Sin embargo, ahora hay que notar que puede continuar, factorizando$3$ de ambos$15a$ y$12$.

$=3(5 a-4)(a+b)$

Obsérvese que el orden de los factores difiere de la primera solución, pero debido a la propiedad conmutativa de la multiplicación, el orden no importa. Las respuestas son las mismas.

Ejercicio$\PageIndex{12}$

Factor:$24 m(m-2 n)+20(m-2 n)$

Responder

$4(6 m+5)(m-2 n)$

Factorización por Agrupación

La habilidad de factorización final en esta sección involucra expresiones de cuatro términos. La técnica para factorizar una expresión de cuatro términos se denomina factorización por agrupación.

Ejemplo$\PageIndex{13}$

Factor por agrupación:$x^{2}+8 x+3 x+24$

Solución

Nosotros “agrupamos” el primer y segundo término, señalando que podemos factorizar un$x$ de ambos términos. Entonces “agruparemos” los términos tercero y cuarto, señalando que podemos factorizar$3$ de ambos términos.

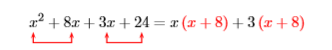
Ahora podemos$x + 8$ factorizar de ambos términos.

$(x+3){\color {Red}(x+8)}$

Ejercicio$\PageIndex{13}$

Factor por agrupación:$x^{2}-6 x+2 x-12$

Responder

$(x+2)(x-6)$

Probemos con una agrupación que contenga algunos signos negativos.

Ejemplo$\PageIndex{14}$

Factor por agrupación:$x^{2}+4 x-7 x-28$

Solución

Nosotros “agrupamos” el primer y segundo término, señalando que podemos factorizar$x$ de ambos términos. Entonces “agrupamos” los términos tercero y cuarto, luego tratamos de factorizar a de ambos términos.$7$

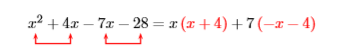
Esto no lleva a un factor común. Vamos a intentarlo de nuevo, esta vez factorizando un$−7$ fuera del tercer y cuarto términos.

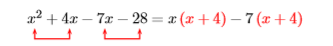
¡Eso funcionó! Ahora factorizamos un factor común$x + 4$.

$(x-7){\color {Red}(x+4)}$

Ejercicio$\PageIndex{14}$

Factor por agrupación:$x^{2}-5 x-4 x+20$

Responder

$(x-4)(x-5)$

Aumentemos un poco el tamaño de los números.

Ejemplo$\PageIndex{15}$

Factor por agrupación:$6 x^{2}-8 x+9 x-12$

Solución

Tenga en cuenta que podemos$2x$ factorizar de los dos primeros términos y$3$ de los dos segundos términos.

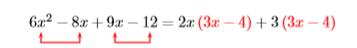
Ahora tenemos un factor común$3x−4$ que podemos factorizar.

$(2x+3){\color {Red}(3x-4)}$

Ejercicio$\PageIndex{15}$

Factor por agrupación:$15 x^{2}+9 x+10 x+6$

Responder

$(3 x+2)(5 x+3)$

A medida que los números se hacen cada vez más grandes, es necesario factorizar el ($\mathrm{GCF}$) de cada agrupación. Si no, no obtendrá un factor común para finalizar el factoring.

Ejemplo$\PageIndex{16}$

Factor por agrupación:$24 x^{2}-32 x-45 x+60$

Solución

Supongamos que$8x$ factorizamos de los dos primeros términos y$−5$ de los dos segundos términos.

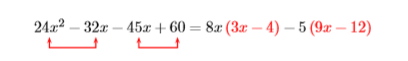
Eso no funcionó, ya que no tenemos un factor común para completar el proceso de factorización. Sin embargo, tenga en cuenta que todavía podemos factorizar un$3$ de$9x−12$. Como ya hemos factorizado un$5$, y ahora vemos puede factorizar un adicional$3$, esto significa que deberíamos haber factorizado los$3$ tiempos$5$, o$15$, para empezar. Empecemos de nuevo, sólo que esta vez vamos a factorizar$15$ fuera de los dos segundos términos.

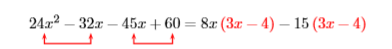
¡Hermoso! Ahora podemos factorizar$3x−4$.

$(8x-15){\color {Red}(3x-4)}$

Ejercicio$\PageIndex{16}$

Factor por agrupación:$36 x^{2}-84 x+15 x-35$

Responder

$(12 x+5)(3 x-7)$