6.7: Aplicaciones de Factoring

En esta sección resolveremos aplicaciones cuyas soluciones involucren factorización. Empecemos.

Ejemplo$\PageIndex{1}$

Un cuadro rectangular en lienzo mide$12$ pulgadas por$16$ pulgadas. El lienzo se monta dentro de un marco de ancho uniforme, aumentando el área total cubierta tanto por la lona como por el marco a pulgadas$396$ cuadradas. Encuentra el ancho uniforme del marco.

Solución

Seguimos los Requisitos para Soluciones de Problemas de Word.

1. Configurar un diccionario de variables: Una figure cuidadosamente etiquetada nos ayudará a mantener nuestro enfoque. Vamos a dejar$x$ representar el ancho uniforme del marco.

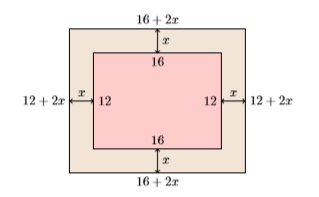
2. Configura una ecuación: Si las dimensiones rectangulares internas son$16$ pulgadas por$12$ pulgadas, agregar un marco de ancho uniforme$x$ hace que las dimensiones del marco más el lienzo$16 + 2x$ pulgadas por$12 + 2x$ pulgadas. El área total se encuentra multiplicando estas dimensiones exteriores,$A = (16 + 2x)(12 + 2x)$. Si el área total es de pulgadas$A = 396$ cuadradas, entonces tenemos la siguiente ecuación. $$(16 + 2x)(12 + 2x) = 396 \nonumber$$
3. Resuelve la ecuación: Comenzamos expandiendo el lado derecho de la ecuación. $$\begin{align*} (16 + 2x)(12 + 2x) &= 396\\ 192 + 56x +4x^2 &= 396 \end{align*} \nonumber$$ La ecuación resultante es no lineal. Hacer un lado cero. $$4x^2 + 56x−204 = 0 \nonumber$$ Podríamos factorial$4$ en el lado izquierdo, pero como hay un cero en el lado derecho de la ecuación, es un poco más fácil simplemente dividir ambos lados por$4$. Observe cómo dividimos cada término del lado izquierdo por el número$4$. $$x^2 + 14x−51 = 0 \nonumber$$ Necesitamos un par entero cuyo producto es$ac = −51$ y cuya suma es$b = 14$. El par entero$−3,17$ viene a la mente. Dado que el coecient de$x^2$ es uno, simplemente podemos “colocar en su lugar” nuestro par ordenado. $$(x−3)(x + 17) = 0 \nonumber$$ Así, las soluciones son$x = 3$ y$x = −17$.
4. Responda a la pregunta: El ancho uniforme del marco no puede ser$−17$ pulgadas, por lo que eliminamos esta solución de consideración. De ahí que el ancho uniforme del marco sea de$3$ pulgadas.
5. Mirar atrás: Si el ancho uniforme del marco es$3$ pulgadas, entonces las dimensiones finales se verán como las siguientes.

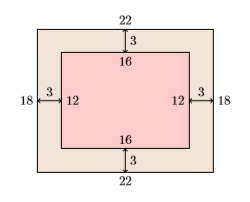
Así, el área combinada del marco más lienzo es$A = (18)(22)$, o pulgadas$A = 396$ cuadradas, el área dada en la declaración del problema. Nuestra solución es correcta.

Ejercicio$\PageIndex{1}$

Un cuadro rectangular en lienzo mide$7$ pulgadas por$11$ pulgadas. El lienzo se monta dentro de un marco de ancho uniforme, aumentando el área total cubierta tanto por la lona como por el marco a pulgadas$117$ cuadradas. Encuentra el ancho uniforme del marco.

Contestar

$1$pulgada

Ejemplo$\PageIndex{2}$

Un proyectil es disparado en ángulo hacia el aire desde lo alto de un clítoris con vista al océano. La distancia del proyectil (en pies) desde la base del cli, viene dada por la ecuación $$x = 120t \label{Eq6.7.1}$$ y la altura del proyectil sobre el nivel del mar (en pies) viene dada por la ecuación $$y = −16t^2 + 288t + 640 \label{Eq6.7.2}$$ donde$t$ está la cantidad de tiempo (en segundos) que ha pasado desde la liberación del proyectil.

1. ¿Cuánto tiempo pasa antes de que el proyectil salpique en el océano?
2. En ese momento, ¿a qué distancia se encuentra el proyectil de la base del clítoris?

Solución

Seguimos los Requisitos para Soluciones de Problemas de Word.

1. Configurar un diccionario de variables: Las variables ya están establecidas para nosotros. $$\begin{align*} x &= \text {Distance from base of the cliff (in feet).}\\ y &= \text {Height above sea level (in feet).}\\ t &= \text {Time since projectile's release (in seconds).} \end{align*}\nonumber$$
2. Configurar una ecuación: Las ecuaciones ya están establecidas (ver Ecuación\ ref {Eq6.7.1} y Ecuación\ ref {Eq6.7.2}).
3. Resuelve la ecuación: Cuando el proyectil salpica en el océano, su altura sobre el nivel del mar en ese momento es de$y = 0$ pies. Sustituir$0$$y$ en Ecuación\ ref {Eq6.7.2} y resolver la ecuación resultante para$t$. $$\begin{align*} y &= -16t^2 + 288t + 640\\ 0 &= -16t^2 + 288t + 640 \end{align*}\nonumber$$ Podríamos factorial$−16$, pero como el lado izquierdo de esta ecuación es cero, es un poco más fácil dividir ambos lados por$−16$. Observe cómo dividimos cada término en el lado derecho por$−16$. $$0=t^2 −18t−40 \nonumber$$ Necesitamos un par de enteros para que su producto sea$ac = −40$ y su suma sea$−18$. El par entero$2$, me$−20$ viene a la mente. Dado que el coecient de$t^2$ es uno, podemos “colocar en su lugar” nuestro par entero. $$0=( t + 2)( t−20) \nonumber$$ De ahí que las soluciones sean$t = −2$ y$t = 20$.
4. Responda a la pregunta: Al responder a la pregunta (a), los$t = −2$ segundos de solución no tienen sentido. Así, el proyectil salpica en el océano a los$t = 20$ segundos. Al abordar la pregunta b), para encontrar la distancia del proyectil con respecto a la base del clítoris en este momento, sustituya$t = 20$ en la Ecuación\ ref {Eq6.7.1}. $$\begin{align*} x &= 120t\\ x &= 120(20)\\ x &= 2400 \end{align*}\nonumber$$ De ahí que en el momento en que el proyectil salpica hacia el océano, se encuentra a$2,400$ pies de la base del clítoris.
5. Mira atrás: Lo mejor que podemos hacer aquí es consultar nuestra solución$t = 20$ en Ecuación\ ref {Eq6.7.2}. $$\begin{align*} y &= -16t^2 + 288t + 640 \\ y &= -16(20)2 + 288(20)+ 640 \\ y &= -6400+ 5760 + 640 \\ y &= 0 \end{align*}\nonumber$$ En efecto, a$t = 20$, el proyectil sí chapotea en el océano.

Ejercicio$\PageIndex{2}$

La altura de un proyectil (en pies) viene dada por la ecuación$y = −16t^2 + 144t + 576$, donde el tiempo$t$ se mide en segundos. ¿Cuánto tiempo pasa antes de que el proyectil golpee el suelo?

Contestar

$12$segundos

Ejemplo$\PageIndex{3}$

El producto de dos enteros pares consecutivos es$728$. Encuentra los enteros.

Solución

Seguimos los Requisitos para Soluciones de Problemas de Word.

1. Configurar un diccionario de variables: Let$k$ representar el primer entero par. Entonces$k + 2$ representa el siguiente entero par consecutivo.
2. Configurar una ecuación: El producto de los enteros es$728$. De ahí que tengamos la siguiente ecuación. $$k(k + 2) = 728 \nonumber$$
3. Resuelve la ecuación: Expande el lado izquierdo de la ecuación. $$k^2 +2k = 728 \nonumber$$ La ecuación es no lineal. Hacer un lado cero. $$k^2 +2k−728 = 0 \nonumber$$ Consulte Uso de la Calculadora para Asistir al$ac$ Método. Necesitamos un par entero cuyo producto es$ac = −728$ y cuya suma es$b = 2$. $-728/X$Ingresa$\mathrm{Y1}$, luego configura la tabla (ver Figura$\PageIndex{1}$).

Figura$\PageIndex{1}$: Cargar$ac/X$, o$-728/X$$\mathrm{Y1}$ en el menú Y=.

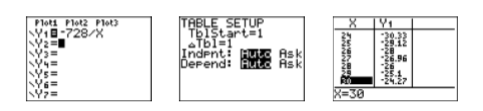
Usa las teclas de flecha arriba y abajo para desplazarte. Tenga en cuenta que$28,−26$ es el par deseado. Debido a que el coecient de$k^2$ es uno, podemos “colocar en su lugar” el par ordenado.

$$0=( k + 28)(k−26) \nonumber$$ De ahí que las soluciones sean$k = −28$ y$k = 26$.

4. Responde a la pregunta: Si$k = −28$, el siguiente entero par consecutivo es$k +2=−26$. En segundo lugar$k = 26$, si, el siguiente entero par consecutivo es$k + 2 = 28$.
5. Mirar atrás: Nuestro primer par es$−28$ y$−26$. Cuentan con el producto requerido de$728$. Nuestro segundo par es$26$ y$28$. Su producto también lo es$728$. Ambas soluciones verifican!

Ejercicio$\PageIndex{3}$

El producto de dos enteros impares positivos consecutivos es$483$. Encuentra los enteros.

Contestar

$21$y$23$

Ejemplo$\PageIndex{4}$

Un rectángulo tiene$54$ pies perimetrales y área de pies$180$ cuadrados. Encuentra las dimensiones del rectángulo.

Solución

Seguimos los Requisitos para Soluciones de Problemas de Word.

1. Configurar un diccionario de variables: Un boceto nos ayudará a mantener nuestro enfoque. Dejar$L$ representar la longitud del rectángulo y dejar$W$ representar su ancho.

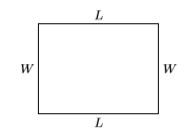
2. Establecer una ecuación: El perímetro es$54$ pies, así$2W+2L = 54$, o dividiendo ambos lados por$2$: $$W + L = 27 \label{Eq6.7.3}$$ El área es pies$180$ cuadrados, entonces: $$LW = 180 \label{Eq6.7.4}$$
3. Resuelve la ecuación: El sistema de ecuaciones (ecuaciones\ ref {Eq6.7.3} y\ ref {Eq6.7.4}) se puede resolver usando el método de sustitución. Primero, resuelve la Ecuación\ ref {Eq6.7.3} para$W$: Ecuación $$W = 27−L \label{Eq6.7.5}$$ sustituta\ ref {Eq6.7.5} en la Ecuación\ ref {Eq6.7.4}, expandir, luego hacer un lado cero. $$\begin{align*} L(27-L) &= 180 \\ 27L-L^2 &= 180 \\ 0 &= L^2-27L+180 \end{align*}\nonumber$$ El par entero$−12,−15$ tiene producto$ac = 180$ y suma$b = −27$. Además, el coecient de$L^2$ es uno, así que podemos “colocar en su lugar” nuestro par entero. $$0=(L−12)(L−15) \nonumber$$ De ahí que las soluciones sean$L = 12$ y$L = 15$.
4. Responde a la pregunta: Dos posibilidades para el ancho.
   1. Sustituto$L = 12$ en\ ref {Eq6.7.5}. $$\begin{align*} W &= 27-L \\ W &= 27-12 \\ W &= 15 \end{align*}\nonumber$$
   2. Sustituto$L = 15$ en\ ref {Eq6.7.5}. $$\begin{align*} W &= 27-L \\ W &= 27-15 \\ W &= 12 \end{align*}\nonumber$$

Ambas respuestas dan lo mismo$15$ por rectángulo de$12$ pie, pero solemos pensar en el término “longitud” como el lado más largo del rectángulo.

Entonces vamos con el largo es$L = 15$ pies y el ancho es$W = 12$ pies.

5. Mirar atrás: Agreguemos$L = 15$ pies y$W = 12$ pies a un diagrama.

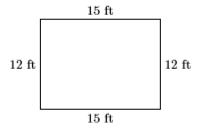
Si agregamos las dimensiones alrededor del rectángulo, el perímetro es$P = 15+12 +15+ 12$, o$P = 54$ pies, el perímetro requerido en la declaración del problema.

A continuación, si multiplicamos las dimensiones, entonces$A = (15)(12)$, o pies$A = 180$ cuadrados, el área requerida en la declaración del problema. ¡Nuestra solución es correcta!

Ejercicio$\PageIndex{4}$

Un rectángulo tiene$62$ pies perimetrales y área de pies$234$ cuadrados. Encuentra las dimensiones del rectángulo.

Contestar

largo =$18$ pies y ancho =$13$ pies