6.E: Factoring (Ejercicios)

6.1: El mayor factor común

En los Ejercicios 1-6, enumere todos los divisores positivos del número dado, en orden, de menor a mayor.

1)\(42\)

Contestar: \(\{1,2,3,6,7,14,21,42\}\)

2)\(60\)

3)\(44\)

Contestar: \(\{1,2,4,11,22,44\}\)

4)\(85\)

5)\(51\)

Contestar: \(\{1,3,17,51\}\)

6)\(63\)

En los Ejercicios 7-12, enumere todos los divisores positivos comunes de los números dados, en orden, de menor a mayor.

7)\(36\) y\(42\)

Contestar: \(\{1,2,3,6\}\)

8)\(54\) y\(30\)

9)\(78\) y\(54\)

Contestar: \(\{1,2,3,6\}\)

10)\(96\) y\(78\)

11)\(8\) y\(76\)

Contestar: \(\{1,2,4\}\)

12)\(99\) y\(27\)

En los Ejercicios 13-18, declarar el mayor divisor común de los números dados.

13)\(76\) y\(8\)

Responder: \(4\)

14)\(84\) y\(60\)

15)\(32\) y\(36\)

Responder: \(4\)

16)\(64\) y\(76\)

17)\(24\) y\(28\)

Responder: \(4\)

18)\(63\) y\(27\)

En los Ejercicios 19-24, utilice la factorización de primos para ayudar a calcular el mayor divisor común de los números dados.

19)\(600\) y\(1080\)

Responder: \(120\)

20)\(150\) y\(120\)

21)\(1800\) y\(2250\)

Responder: \(450\)

22)\(540\) y\(150\)

23)\(600\) y\(450\)

Responder: \(150\)

24)\(4500\) y\(1800\)

En los Ejercicios 25-36, encontramos el mayor factor común de las expresiones dadas.

25)\(16b^{4}\) y\(56b^{9}\)

Responder: \(8b^{4}\)

26)\(28s^{2}\) y\(36s^{4}\)

27)\(35z^{2}\) y\(49z^{7}\)

Responder: \(7z^{2}\)

28)\(24w^{3}\) y\(30w^{8}\)

29)\(56x^{3} y^{4}\) y\(16x^{2} y^{5}\)

Responder: \(8 x^{2} y^{4}\)

30)\(35b^{5} c^{3}\) y\(63b^{4} c^{4}\)

31)\(24s^{4} t^{5}\) y\(16s^{3} t^{6}\)

Responder: \(8 s^{3} t^{5}\)

32)\(10v^{4} w^{3}\) y\(8v^{3} w^{4}\)

33)\(18 y^{7}\),\(45 y^{6}\), y\(27y^{5}\)

Responder: \(9 y^{5}\)

34)\(8 r^{7}\),\(24 r^{6}\), y\(12r^{5}\)

35)\(9 a^{6}\),\(6 a^{5}\), y\(15a^{4}\)

Responder: \(3 a^{4}\)

36)\(15 a^{5}\),\(24 a^{4}\), y\(24a^{3}\)

En los Ejercicios 37-52, factorizar el\(\mathrm{GCF}\) de cada una de las expresiones dadas.

37)\(25 a^{2}+10 a+20\)

Responder: \(5\left(5 a^{2}+2 a+4\right)\)

38)\(40 c^{2}+15 c+40\)

39)\(35 s^{2}+25 s+45\)

Responder: \(5\left(7 s^{2}+5 s+9\right)\)

40)\(45 b^{2}+20 b+35\)

41)\(16 c^{3}+32 c^{2}+36 c\)

Responder: \(4 c\left(4 c^{2}+8 c+9\right)\)

42)\(12 b^{3}+12 b^{2}+18 b\)

43)\(42 s^{3}+24 s^{2}+18 s\)

Responder: \(6 s\left(7 s^{2}+4 s+3\right)\)

44)\(36 y^{3}+81 y^{2}+36 y\)

45)\(35 s^{7}+49 s^{6}+63 s^{5}\)

Responder: \(7 s^{5}\left(5 s^{2}+7 s+9\right)\)

46)\(35 s^{7}+56 s^{6}+56 s^{5}\)

47)\(14 b^{7}+35 b^{6}+56 b^{5}\)

Responder: \(7 b^{5}\left(2 b^{2}+5 b+8\right)\)

48)\(45 x^{5}+81 x^{4}+45 x^{3}\)

49)\(54 y^{5} z^{3}+30 y^{4} z^{4}+36 y^{3} z^{5}\)

Responder: \(6 y^{3} z^{3}\left(9 y^{2}+5 y z+6 z^{2}\right)\)

50)\(42 x^{4} y^{2}+42 x^{3} y^{3}+54 x^{2} y^{4}\)

51)\(45 s^{4} t^{3}+40 s^{3} t^{4}+15 s^{2} t^{5}\)

Responder: \(5.8^{2} t^{3}\left(9 s^{2}+8 s t+3 t^{2}\right)\)

52)\(20 v^{6} w^{3}+36 v^{5} w^{4}+28 v^{4} w^{5}\)

En los Ejercicios 53-60, factorizar el\(\mathrm{GCF}\) de cada una de las expresiones dadas.

53)\(7 w(2 w-3)-8(2 w-3)\)

Responder: \((7 w-8)(2 w-3)\)

54)\(5 s(8 s-1)+4(8 s-1)\)

55)\(9 r(5 r-1)+8(5 r-1)\)

Responder: \((9 r+8)(5 r-1)\)

56)\(5 c(4 c-7)+2(4 c-7)\)

57)\(48 a(2 a+5)-42(2 a+5)\)

Responder: \(6(2 a+5)(8 a-7)\)

58)\(40 v(7 v-4)+72(7 v-4)\)

59)\(56 a(2 a-1)-21(2 a-1)\)

Responder: \(7(2 a-1)(8 a-3)\)

60)\(48 r(5 r+3)-40(5 r+3)\)

En Ejercicios 61-68, factorizar por agrupación. No simplifique la expresión antes de factorizar.

61)\(x^{2}+2 x-9 x-18\)

Responder: \((x-9)(x+2)\)

62)\(x^{2}+6 x-9 x-54\)

63)\(x^{2}+3 x+6 x+18\)

Responder: \((x+6)(x+3)\)

64)\(x^{2}+8 x+7 x+56\)

65)\(x^{2}-6 x-3 x+18\)

Responder: \((x-3)(x-6)\)

66)\(x^{2}-3 x-9 x+27\)

67)\(x^{2}-9 x+3 x-27\)

Responder: \((x+3)(x-9)\)

68)\(x^{2}-2 x+7 x-14\)

En Ejercicios 69-76, factorizar por agrupación. No simplifique la expresión antes de factorizar.

69)\(8 x^{2}+3 x-56 x-21\)

Responder: \((x-7)(8 x+3)\)

70)\(4 x^{2}+9 x-32 x-72\)

71)\(9 x^{2}+36 x-5 x-20\)

Responder: \((9 x-5)(x+4)\)

72)\(7 x^{2}+14 x-8 x-16\)

73)\(6 x^{2}-7 x-48 x+56\)

Responder: \((x-8)(6 x-7)\)

74)\(8 x^{2}-7 x-72 x+63\)

75)\(2 x^{2}+12 x+7 x+42\)

Responder: \((2 x+7)(x+6)\)

76)\(7 x^{2}+28 x+9 x+36\)

6.2: Resolver ecuaciones no lineales

En los Ejercicios 1-8, resuelve la ecuación dada para\(x\).

1)\((9 x+2)(8 x+3)=0\)

Responder: \(x=-\dfrac{2}{9},-\dfrac{3}{8}\)

2)\((2 x-5)(7 x-4)=0\)

3)\(x(4 x+7)(9 x-8)=0\)

Responder: \(x=0,-\dfrac{7}{4}, \dfrac{8}{9}\)

4)\(x(9 x-8)(3 x+1)=0\)

5)\(-9 x(9 x+4)=0\)

Responder: \(x=0,-\dfrac{4}{9}\)

6)\(4 x(3 x-6)=0\)

7)\((x+1)(x+6)=0\)

Responder: \(x=-1,-6\)

8)\((x-4)(x-1)=0\)

En los Ejercicios 9-18, dado que estás resolviendo para\(x\), indica si la ecuación dada es lineal o no lineal. No resuelva la ecuación.

9)\(x^{2}+7 x=9 x+63\)

Responder: No lineal

10)\(x^{2}+9 x=4 x+36\)

11)\(6 x-2=5 x-8\)

Responder: Lineal

12)\(-5 x+5=-6 x-7\)

13)\(7 x^{2}=-2 x\)

Responder: No lineal

14)\(4 x^{2}=-7 x\)

15)\(3 x^{2}+8 x=-9\)

Responder: No lineal

16)\(5 x^{2}-2 x=-9\)

17)\(-3 x+6=-9\)

Responder: Lineal

18)\(8 x-5=3\)

En Ejercicios 19-34, resolver cada una de las ecuaciones dadas para\(x\).

19)\(3 x+8=9\)

Responder: \(\dfrac{1}{3}\)

20)\(3 x+4=2\)

21)\(9 x^{2}=-x\)

Responder: \(x=0,-\dfrac{1}{9}\)

22)\(6 x^{2}=7 x\)

23)\(3 x+9=8 x+7\)

Responder: \(\dfrac{2}{5}\)

24)\(8 x+5=6 x+4\)

25)\(8 x^{2}=-2 x\)

Responder: \(x=0,-\dfrac{1}{4}\)

26)\(8 x^{2}=18 x\)

27)\(9 x+2=7\)

Responder: \(\dfrac{5}{9}\)

28)\(3 x+2=6\)

29)\(9 x^{2}=6 x\)

Responder: \(x=0, \dfrac{2}{3}\)

30)\(6 x^{2}=-14 x\)

31)\(7 x^{2}=-4 x\)

Responder: \(x=0,-\dfrac{4}{7}\)

32)\(7 x^{2}=-9 x\)

33)\(7 x+2=4 x+7\)

Responder: \(\dfrac{5}{3}\)

34)\(4 x+3=2 x+8\)

En Ejercicios 35-50, factorizar por agrupación para resolver cada una de las ecuaciones dadas para\(x\).

35)\(63 x^{2}+56 x+54 x+48=0\)

Responder: \(x=-\dfrac{6}{7},-\dfrac{8}{9}\)

36)\(27 x^{2}+36 x+6 x+8=0\)

37)\(16 x^{2}-18 x+40 x-45=0\)

Responder: \(x=-\dfrac{5}{2}, \dfrac{9}{8}\)

38)\(42 x^{2}-35 x+54 x-45=0\)

39)\(45 x^{2}+18 x+20 x+8=0\)

Responder: \(x=-\dfrac{4}{9},-\dfrac{2}{5}\)

40)\(18 x^{2}+21 x+30 x+35=0\)

41)\(x^{2}+10 x+4 x+40=0\)

Responder: \(x=-4,-10\)

42)\(x^{2}+11 x+10 x+110=0\)

43)\(x^{2}+6 x-11 x-66=0\)

Responder: \(x=11,-6\)

44)\(x^{2}+6 x-2 x-12=0\)

45)\(15 x^{2}-24 x+35 x-56=0\)

Responder: \(x=-\dfrac{7}{3}, \dfrac{8}{5}\)

46)\(12 x^{2}-10 x+54 x-45=0\)

47)\(x^{2}+2 x+9 x+18=0\)

Responder: \(x=-9,-2\)

48)\(x^{2}+8 x+4 x+32=0\)

49)\(x^{2}+4 x-8 x-32=0\)

Responder: \(x=8,-4\)

50)\(x^{2}+8 x-5 x-40=0\)

En los Ejercicios 51-54, realiza cada una de las siguientes tareas:

Utilizar una técnica estrictamente algebraica para resolver la ecuación dada.
Utilice la utilidad 5:intersect en su calculadora gráfica para resolver la ecuación dada.

Reporte los resultados encontrados usando la calculadora gráfica como se muestra en el Ejemplo 6.2.7.

51)\(x^{2}=-4 x\)

Responder: \(x=-4,0\)

52)\(x^{2}=6 x\)

53)\(x^{2}=5 x\)

Responder: \(x=0,5\)

54)\(x^{2}=-6 x\)

En Ejercicios 55-58, realice cada una de las siguientes tareas:

Utilizar una técnica estrictamente algebraica para resolver la ecuación dada.
Utilice la utilidad 2:cero en su calculadora gráfica para resolver la ecuación dada.

Reporte los resultados encontrados usando la calculadora gráfica como se muestra en el Ejemplo 6.2.8.

55)\(x^{2}+7 x=0\)

Responder: \(x=-7,0\)

56)\(x^{2}-8 x=0\)

57)\(x^{2}-3 x=0\)

Responder: \(x=0,3\)

58)\(x^{2}+2 x=0\)

6.3: Factorización ax² + bx + c cuando a =1

En los Ejercicios 1-6, compare el trinomio dado con\(ax^2 + bx + c\), luego enumere TODOS los pares enteros cuyo producto sea igual\(ac\). Encierra en círculo el par cuya suma es igual\(b\), luego usa este par para ayudar a factorizar el trinomio dado.

1)\(x^{2}+7 x-18\)

Responder: \((x-2)(x+9)\)

2)\(x^{2}+18 x+80\)

3)\(x^{2}-10 x+9\)

Contestar: \((x-1)(x-9)\)

4)\(x^{2}+12 x+27\)

5)\(x^{2}+14 x+45\)

Contestar: \((x+5)(x+9)\)

6)\(x^{2}+9 x+20\)

En los Ejercicios 7-12, compare el trinomio dado con\(ax^2 +bx+c\), luego comience a enumerar pares enteros cuyo producto sea igual\(ac\). Cese el proceso de lista cuando descubras un par cuya suma es igual\(b\), luego da un círculo y usa este par para ayudar a factorizar el trinomio dado.

7)\(x^{2}-16 x+39\)

Contestar: \((x-3)(x-13)\)

8)\(x^{2}-16 x+48\)

9)\(x^{2}-26 x+69\)

Contestar: \((x-3)(x-23)\)

10)\(x^{2}-22 x+57\)

11)\(x^{2}-25 x+84\)

Contestar: \((x-4)(x-21)\)

12)\(x^{2}+13 x-30\)

En los Ejercicios 13-18, compare el trinomio dado con\(ax^2 + bx + c\), luego cómpielo\(ac\). Intenta descubrir mentalmente el par entero cuyo producto es\(ac\) y cuya suma es\(b\). Factorizar el trinomio “dejando caer este par en su lugar”.

Nota: Si descubres que no puedes identificar mentalmente al par, comienza a enumerar pares enteros cuyo producto es igual\(ac\), luego cesa el proceso de listado cuando te encuentres con el par cuya suma sea igual\(b\).

13)\(x^{2}-13 x+36\)

Contestar: \((x-4)(x-9)\)

14)\(x^{2}+x-12\)

15)\(x^{2}+10 x+21\)

Contestar: \((x+3)(x+7)\)

16)\(x^{2}-17 x+66\)

17)\(x^{2}-4 x-5\)

Contestar: \((x+1)(x-5)\)

18)\(x^{2}-20 x+99\)

En los Ejercicios 19-24, utilizar una técnica algebraica para resolver la ecuación dada.

19)\(x^{2}=-7 x+30\)

Contestar: \(x=3,-10\)

20)\(x^{2}=-2 x+35\)

21)\(x^{2}=-11 x-10\)

Contestar: \(x=-1,-10\)

22)\(x^{2}=x+72\)

23)\(x^{2}=-15 x-50\)

Contestar: \(x=-5,-10\)

24)\(x^{2}=-7 x-6\)

En los Ejercicios 25-30, utilizar una técnica algebraica para resolver la ecuación dada.

25)\(60=x^{2}+11 x\)

Contestar: \(x=4,-15\)

26)\(-92=x^{2}-27 x\)

27)\(-11=x^{2}-12 x\)

Contestar: \(x=1,11\)

28)\(80=x^{2}-16 x\)

29)\(56=x^{2}+10 x\)

Contestar: \(x=4,-14\)

30)\(66=x^{2}+19 x\)

En los Ejercicios 31-36, utilizar una técnica algebraica para resolver la ecuación dada.

31)\(x^{2}+20=-12 x\)

Contestar: \(x=-2,-10\)

32)\(x^{2}-12=11 x\)

33)\(x^{2}-36=9 x\)

Contestar: \(x=-3,12\)

34)\(x^{2}+6=5 x\)

35)\(x^{2}+8=-6 x\)

Contestar: \(x=-2,-4\)

36)\(x^{2}+77=18 x\)

En los Ejercicios 37-40, realiza cada una de las siguientes tareas:

Utilizar una técnica estrictamente algebraica para resolver la ecuación dada.
Utilice la utilidad 5:intersect en su calculadora gráfica para resolver la ecuación dada.

Reporte los resultados encontrados usando la calculadora gráfica como se muestra en el Ejemplo 6.3.6.

37)\(x^{2}=x+12\)

Contestar: \(x=-3,4\)

38)\(x^{2}=20-x\)

39)\(x^{2}+12=8 x\)

Contestar: \(x=2,6\)

40)\(x^{2}+7=8 x\)

En los Ejercicios 41-44, realiza cada una de las siguientes tareas:

Utilizar una técnica estrictamente algebraica para resolver la ecuación dada.
Utilice la utilidad 2:cero en su calculadora gráfica para resolver la ecuación dada.

Reporte los resultados encontrados usando la calculadora gráfica como se muestra en el Ejemplo 6.3.7.

41)\(x^{2}-6 x-16=0\)

Contestar: \(x=8,-2\)

42)\(x^{2}+7 x-18=0\)

43)\(x^{2}+10 x-24=0\)

Contestar: \(x=-12,2\)

44)\(x^{2}-9 x-36=0\)

6.4: Factorización ax² + bx + c cuando a≠ 1

En los Ejercicios 1-6, compare el trinomio dado con\(ax^2 + bx + c\), luego enumere TODOS los pares enteros cuyo producto sea igual\(ac\). Encierra en círculo el par cuya suma es igual\(b\), luego usa este par para ayudar a factorizar el trinomio dado.

1)\(6 x^{2}+13 x-5\)

Contestar: \((2 x+5)(3 x-1)\)

2)\(3 x^{2}-19 x+20\)

3)\(4 x^{2}-x-3\)

Contestar: \((x-1)(4 x+3)\)

4)\(6 x^{2}-23 x+7\)

5)\(3 x^{2}+19 x+28\)

Contestar: \((x+4)(3 x+7)\)

6)\(2 x^{2}-9 x-18\)

En los Ejercicios 7-12, compare el trinomio dado con\(ax^2 +bx+c\), luego comience a enumerar pares enteros cuyo producto sea igual\(ac\). Cese el proceso de lista cuando descubras un par cuya suma es igual\(b\), luego da un círculo y usa este par para ayudar a factorizar el trinomio dado.

7)\(12 x^{2}-23 x+5\)

Contestar: \((3 x-5)(4 x-1)\)

8)\(8 x^{2}+22 x+9\)

9)\(6 x^{2}+17 x+7\)

Contestar: \((2 x+1)(3 x+7)\)

10)\(4 x^{2}+19 x+21\)

11)\(3 x^{2}+4 x-32\)

Contestar: \((x+4)(3 x-8)\)

12)\(4 x^{2}+x-14\)

En los Ejercicios 13-18, compare el trinomio dado con\(ax^2 + bx + c\), luego cómpielo\(ac\). Intenta descubrir mentalmente el par entero cuyo producto es\(ac\) y cuya suma es\(b\). Usa este par para ayudar a factorizar el trinomio dado.

Nota: Si descubres que no puedes identificar mentalmente al par, comienza a enumerar pares enteros cuyo producto es igual\(ac\), luego cesa el proceso de listado cuando te encuentres con el par cuya suma sea igual\(b\).

13)\(3 x^{2}+28 x+9\)

Contestar: \((3 x+1)(x+9)\)

14)\(6 x^{2}+x-1\)

15)\(4 x^{2}-21 x+5\)

Contestar: \((x-5)(4 x-1)\)

16)\(4 x^{2}-x-14\)

17)\(6 x^{2}-11 x-7\)

Contestar: \((3 x-7)(2 x+1)\)

18)\(2 x^{2}-17 x+21\)

En Ejercicios 19-26, factorizar el trinomio.

19)\(16 x^{5}-36 x^{4}+14 x^{3}\)

Contestar: \(2 x^{3}(2 x-1)(4 x-7)\)

20)\(12 x^{4}-20 x^{3}+8 x^{2}\)

21)\(36 x^{4}-75 x^{3}+21 x^{2}\)

Contestar: \(3 x^{2}(3 x-1)(4 x-7)\)

22)\(6 x^{4}-10 x^{3}-24 x^{2}\)

23)\(6 x^{4}-33 x^{3}+42 x^{2}\)

Contestar: \(3 x^{2}(x-2)(2 x-7)\)

24)\(15 x^{3}-10 x^{2}-105 x\)

25)\(16 x^{4}-36 x^{3}-36 x^{2}\)

Contestar: \(4 x^{2}(x-3)(4 x+3)\)

26)\(40 x^{4}-10 x^{3}-5 x^{2}\)

En los Ejercicios 27-38, utilizar una técnica algebraica para resolver la ecuación dada.

27)\((10-8)^{2}-(7-5)^{3}\)

Contestar: \(x=2,-\dfrac{9}{4}\)

28)\(2 x^{2}=7 x-3\)

29)\(3 x^{2}+16=-14 x\)

Contestar: \(x=-2,-\dfrac{8}{3}\)

30)\(2 x^{2}-20=-3 x\)

31)\(3 x^{2}+30=23 x\)

Contestar: \(x=6, \dfrac{5}{3}\)

32)\(6 x^{2}-7=-11 x\)

33)\(-7 x-3=-6 x^{2}\)

Contestar: \(x=-\dfrac{1}{3}, \dfrac{3}{2}\)

34)\(13 x-45=-2 x^{2}\)

35)\(26 x-9=-3 x^{2}\)

Contestar: \(x=-9, \dfrac{1}{3}\)

36)\(-23 x+7=-6 x^{2}\)

37)\(6 x^{2}=-25 x+9\)

Contestar: \(x=\dfrac{1}{3},-\dfrac{9}{2}\)

38)\(2 x^{2}=13 x+45\)

En los Ejercicios 39-42, realiza cada una de las siguientes tareas:

Utilizar una técnica estrictamente algebraica para resolver la ecuación dada.
Utilice la utilidad 2:cero en su calculadora gráfica para resolver la ecuación dada.

Reporte los resultados encontrados usando la calculadora gráfica como se muestra en el Ejemplo 6.4.5.

39)\(2 x^{2}-9 x-5=0\)

Contestar: \(x=-\dfrac{1}{2},5\)

40)\(2 x^{2}+x-28=0\)

41)\(4 x^{2}-17 x-15=0\)

Contestar: \(x=-\dfrac{3}{4},5\)

42)\(3 x^{2}+14 x-24=0\)

En los Ejercicios 43-46, realiza cada una de las siguientes tareas:

Utilizar una técnica estrictamente algebraica para resolver la ecuación dada.
Utilice la utilidad 2:cero en su calculadora gráfica para resolver la ecuación dada.

Reporte los resultados encontrados usando la calculadora gráfica como se muestra en el Ejemplo 6.4.6.

43)\(2 x^{3}=3 x^{2}+20 x\)

Contestar: \(x=0,-\dfrac{5}{2},4\)

44)\(2 x^{3}=3 x^{2}+35 x\)

45)\(10 x^{3}+34 x^{2}=24 x\)

Contestar: \(x=0,-4, \dfrac{3}{5}\)

46)\(6 x^{3}+3 x^{2}=63 x\)

6.5: Factorización de Formularios Especiales

En los Ejercicios 1-8, expanda cada una de las expresiones dadas.

1)\((8 r-3 t)^{2}\)

Contestar: \(64 r^{2}-48 r t+9 t^{2}\)

2)\((6 a+c)^{2}\)

3)\((4 a+7 b)^{2}\)

Contestar: \(16 a^{2}+56 a b+49 b^{2}\)

4)\((4 s+t)^{2}\)

5)\(\left(s^{3}-9\right)^{2}\)

Contestar: \(s^{6}-18 s^{3}+81\)

6)\(\left(w^{3}+7\right)^{2}\)

7)\(\left(s^{2}+6 t^{2}\right)^{2}\)

Contestar: \(s^{4}+12 s^{2} t^{2}+36 t^{4}\)

8)\(\left(7 u^{2}-2 w^{2}\right)^{2}\)

En los Ejercicios 9-28, factorizar cada una de las expresiones dadas.

9)\(25 s^{2}+60 s t+36 t^{2}\)

Contestar: \((5 s+6 t)^{2}\)

10)\(9 u^{2}+24 u v+16 v^{2}\)

11)\(36 v^{2}-60 v w+25 w^{2}\)

Contestar: \((6 v-5 w)^{2}\)

12)\(49 b^{2}-42 b c+9 c^{2}\)

13)\(a^{4}+18 a^{2} b^{2}+81 b^{4}\)

Contestar: \(\left(a^{2}+9 b^{2}\right)^{2}\)

14)\(64 u^{4}-144 u^{2} w^{2}+81 w^{4}\)

15)\(49 s^{4}-28 s^{2} t^{2}+4 t^{4}\)

Contestar: \(\left(7 s^{2}-2 t^{2}\right)^{2}\)

16)\(4 a^{4}-12 a^{2} c^{2}+9 c^{4}\)

17)\(49 b^{6}-112 b^{3}+64\)

Contestar: \(\left(7 b^{3}-8\right)^{2}\)

18)\(25 x^{6}-10 x^{3}+1\)

19)\(49 r^{6}+112 r^{3}+64\)

Contestar: \(\left(7 r^{3}+8\right)^{2}\)

20)\(a^{6}-16 a^{3}+64\)

21)\(5 s^{3} t-20 s^{2} t^{2}+20 s t^{3}\)

Contestar: \(5 s t(s-2 t)^{2}\)

22)\(12 r^{3} t-12 r^{2} t^{2}+3 r t^{3}\)

23)\(8 a^{3} c+8 a^{2} c^{2}+2 a c^{3}\)

Contestar: \(2 a c(2 a+c)^{2}\)

24)\(18 x^{3} z-60 x^{2} z^{2}+50 x z^{3}\)

25)\(-48 b^{3}+120 b^{2}-75 b\)

Contestar: \(-3 b(4 b-5)^{2}\)

26)\(-45 c^{3}+120 c^{2}-80 c\)

27)\(-5 u^{5}-30 u^{4}-45 u^{3}\)

Contestar: \(-5 u^{3}(u+3)^{2}\)

28)\(-12 z^{5}-36 z^{4}-27 z^{3}\)

En los Ejercicios 29-36, expanda cada una de las expresiones dadas.

29)\((21 c+16)(21 c-16)\)

Contestar: \(441 c^{2}-256\)

30)\((19 t+7)(19 t-7)\)

31)\((5 x+19 z)(5 x-19 z)\)

Contestar: \(25 x^{2}-361 z^{2}\)

32)\((11 u+5 w)(11 u-5 w)\)

33)\(\left(3 y^{4}+23 z^{4}\right)\left(3 y^{4}-23 z^{4}\right)\)

Contestar: \(9 y^{8}-529 z^{8}\)

34)\(\left(5 x^{3}+z^{3}\right)\left(5 x^{3}-z^{3}\right)\)

35)\(\left(8 r^{5}+19 s^{5}\right)\left(8 r^{5}-19 s^{5}\right)\)

Contestar: \(64 r^{10}-361 s^{10}\)

36)\(\left(3 u^{3}+16 v^{3}\right)\left(3 u^{3}-16 v^{3}\right)\)

En Ejercicios 37-60, factorizar cada una de las expresiones dadas.

37)\(361 x^{2}-529\)

Contestar: \((19 x+23)(19 x-23)\)

38)\(9 b^{2}-25\)

39)\(16 v^{2}-169\)

Contestar: \((4 v+13)(4 v-13)\)

40)\(81 r^{2}-169\)

41)\(169 x^{2}-576 y^{2}\)

Contestar: \((13 x+24 y)(13 x-24 y)\)

42)\(100 y^{2}-81 z^{2}\)

43)\(529 r^{2}-289 s^{2}\)

Contestar: \((23 r+17 s)(23 r-17 s)\)

44)\(49 a^{2}-144 b^{2}\)

45)\(49 r^{6}-256 t^{6}\)

Contestar: \(\left(7 r^{3}+16 t^{3}\right)\left(7 r^{3}-16 t^{3}\right)\)

46)\(361 x^{10}-484 z^{10}\)

47)\(36 u^{10}-25 w^{10}\)

Contestar: \(\left(6 u^{5}+5 w^{5}\right)\left(6 u^{5}-5 w^{5}\right)\)

48)\(a^{6}-81 c^{6}\)

49)\(72 y^{5}-242 y^{3}\)

Contestar: \(2 y^{3}(6 y+11)(6 y-11)\)

50)\(75 y^{5}-147 y^{3}\)

51)\(1444 a^{3} b-324 a b^{3}\)

Contestar: \(4 a b(19 a+9 b)(19 a-9 b)\)

52)\(12 b^{3} c-1875 b c^{3}\)

53)\(576 x^{3} z-1156 x z^{3}\)

Contestar: \(4 x z(12 x+17 z)(12 x-17 z)\)

54)\(192 u^{3} v-507 u v^{3}\)

55)\(576 t^{4}-4 t^{2}\)

Contestar: \(4 t^{2}(12 t+1)(12 t-1)\)

56)\(4 z^{5}-256 z^{3}\)

57)\(81 x^{4}-256\)

Contestar: \(\left(9 x^{2}+16\right)(3 x+4)(3 x-4)\)

58)\(81 x^{4}-1\)

59)\(81 x^{4}-16\)

Contestar: \(\left(9 x^{2}+4\right)(3 x+2)(3 x-2)\)

60)\(x^{4}-1\)

En los Ejercicios 61-68, factorizar cada una de las expresiones dadas por completo.

61)\(z^{3}+z^{2}-9 z-9\)

Contestar: \((z+3)(z-3)(z+1)\)

62)\(3 u^{3}+u^{2}-48 u-16\)

63)\(x^{3}-2 x^{2} y-x y^{2}+2 y^{3}\)

Contestar: \((x+y)(x-y)(x-2 y)\)

64)\(x^{3}+2 x^{2} z-4 x z^{2}-8 z^{3}\)

65)\(r^{3}-3 r^{2} t-25 r t^{2}+75 t^{3}\)

Contestar: \((r+5 t)(r-5 t)(r-3 t)\)

66)\(2 b^{3}-3 b^{2} c-50 b c^{2}+75 c^{3}\)

67)\(2 x^{3}+x^{2}-32 x-16\)

Contestar: \((x+4)(x-4)(2 x+1)\)

68)\(r^{3}-2 r^{2}-r+2\)

En Ejercicios 69-80, resolver cada una de las ecuaciones dadas para\(x\).

69)\(2 x^{3}+7 x^{2}=72 x+252\)

Contestar: \(x=-6,6,-\dfrac{7}{2}\)

70)\(2 x^{3}+7 x^{2}=32 x+112\)

71)\(x^{3}+5 x^{2}=64 x+320\)

Contestar: \(x=-8,8,-5\)

72)\(x^{3}+4 x^{2}=49 x+196\)

73)\(144 x^{2}+121=264 x\)

Contestar: \(x=\dfrac{11}{12}\)

74)\(361 x^{2}+529=874 x\)

75)\(16 x^{2}=169\)

Contestar: \(x=-\dfrac{13}{4}, \dfrac{13}{4}\)

76)\(289 x^{2}=4\)

77)\(9 x^{2}=25\)

Contestar: \(x=-\dfrac{5}{3}, \dfrac{5}{3}\)

78)\(144 x^{2}=121\)

79)\(256 x^{2}+361=-608 x\)

Contestar: \(x=-\dfrac{19}{16}\)

80)\(16 x^{2}+289=-136 x\)

En los Ejercicios 81-84, realiza cada una de las siguientes tareas:

Utilizar una técnica estrictamente algebraica para resolver la ecuación dada.
Utilice la utilidad 5:intersect en su calculadora gráfica para resolver la ecuación dada.

Reporte los resultados encontrados usando la calculadora gráfica como se muestra en el Ejemplo 6.5.12.

81)\(x^{3}=x\)

Contestar: \(x=0,-1,1\)

82)\(x^{3}=9 x\)

83)\(4 x^{3}=x\)

Contestar: \(x=0,-\dfrac{1}{2},\dfrac{1}{2}\)

84)\(9 x^{3}=x\)

6.6: Estrategia de Factoring

En los Ejercicios 1-12, factorizar completamente cada uno de los polinomios dados.

1)\(484 y^{4} z^{2}-144 y^{2} z^{4}\)

Contestar: \(4 y^{2} z^{2}(11 y+6 z)(11 y-6 z)\)

2)\(72 s^{4} t^{4}-242 s^{2} t^{6}\)

3)\(3 x^{7} z^{5}-363 x^{5} z^{5}\)

Contestar: \(3 x^{5} z^{5}(x+11)(x-11)\)

4)\(5 r^{5} s^{2}-80 r^{3} s^{2}\)

5)\(2 u^{7}-162 u^{5}\)

Contestar: \(2u^5(u + 9)(u−9) \)

6)\(405 x^{4}-320 x^{2}\)

7)\(3 v^{8}-1875 v^{4}\)

Contestar: \(3v^4(v^2 + 25)(v + 5)(v−5)\)

8)\(3 a^{9}-48 a^{5}\)

9)\(3 x^{6}-300 x^{4}\)

Contestar: \(3 x^{4}(x+10)(x-10)\)

10)\(2 y^{5}-18 y^{3}\)

11)\(1250 u^{7} w^{3}-2 u^{3} w^{7}\)

Contestar: \(2 u^{3} w^{3}\left(25 u^{2}+w^{2}\right)(5 u+w)(5 u-w)\)

12)\(48 y^{8} z^{4}-3 y^{4} z^{8}\)

En los Ejercicios 13-24, factorizar completamente cada uno de los polinomios dados.

13)\(75 a^{6}-210 a^{5}+147 a^{4}\)

Contestar: \(3 a^{4}(5 a-7)^{2}\)

14)\(245 v^{7}-560 v^{6}+320 v^{5}\)

15)\(180 a^{5} b^{3}+540 a^{4} b^{4}+405 a^{3} b^{5}\)

Contestar: \(45 a^{3} b^{3}(2 a+3 b)^{2}\)

16)\(192 u^{6} v^{4}+432 u^{5} v^{5}+243 u^{4} v^{6}\)

17)\(2 b^{5}+4 b^{4}+2 b^{3}\)

Contestar: \(2 b^{3}(b+1)^{2}\)

18)\(3 v^{6}+30 v^{5}+75 v^{4}\)

19)\(2 z^{4}-4 z^{3}+2 z^{2}\)

Contestar: \(2 z^{2}(z-1)^{2}\)

20)\(2 u^{6}-40 u^{5}+200 u^{4}\)

21)\(324 x^{4}+360 x^{3}+100 x^{2}\)

Contestar: \(4 x^{2}(9 x+5)^{2}\)

22)\(98 b^{4}+84 b^{3}+18 b^{2}\)

23)\(75 b^{4} c^{5}-240 b^{3} c^{6}+192 b^{2} c^{7}\)

Contestar: \(3 b^{2} c^{5}(5 b-8 c)^{2}\)

24)\(162 a^{5} c^{4}-180 a^{4} c^{5}+50 a^{3} c^{6}\)

En los Ejercicios 25-36, factorizar completamente cada uno de los polinomios dados.

25)\(5 a^{5}+5 a^{4}-210 a^{3}\)

Contestar: \(5 a^{3}(a-6)(a+7)\)

26)\(3 y^{5}-9 y^{4}-12 y^{3}\)

27)\(3 y^{6}-39 y^{5}+120 y^{4}\)

Contestar: \(3 y^{4}(y-8)(y-5)\)

28)\(3 y^{7}-27 y^{6}+42 y^{5}\)

29)\(3 z^{4}+12 z^{3}-135 z^{2}\)

Contestar: \(3 z^{2}(z-5)(z+9)\)

30)\(5 a^{4}-40 a^{3}-45 a^{2}\)

31)\(4 a^{6}+64 a^{5}+252 a^{4}\)

Contestar: \(4 a^{4}(a+9)(a+7)\)

32)\(4 x^{4}+64 x^{3}+252 x^{2}\)

33)\(3 z^{4}+33 z^{3}+84 z^{2}\)

Contestar: \(3 z^{2}(z+7)(z+4)\)

34)\(5 a^{6}+65 a^{5}+180 a^{4}\)

35)\(5 z^{7}-75 z^{6}+270 z^{5}\)

Contestar: \(5 z^{5}(z-6)(z-9)\)

36)\(3 y^{4}-27 y^{3}+24 y^{2}\)

En los Ejercicios 37-48, factorizar completamente cada uno de los polinomios dados.

37)\(4 b^{3}-22 b^{2}+30 b\)

Contestar: \(2 b(2 b-5)(b-3)\)

38)\(4 b^{6}-22 b^{5}+30 b^{4}\)

39)\(2 u^{4} w^{5}-3 u^{3} w^{6}-20 u^{2} w^{7}\)

Contestar: \(u^{2} w^{5}(u-4 w)(2 u+5 w)\)

40)\(12 x^{5} z^{2}+9 x^{4} z^{3}-30 x^{3} z^{4}\)

41)\(12 x^{4} y^{5}+50 x^{3} y^{6}+50 x^{2} y^{7}\)

Contestar: \(2 x^{2} y^{5}(3 x+5 y)(2 x+5 y)\)

42)\(24 s^{4} t^{3}+62 s^{3} t^{4}+40 s^{2} t^{5}\)

43)\(12 x^{3}+9 x^{2}-30 x\)

Contestar: \(3 x(4 x-5)(x+2)\)

44)\(6 v^{4}+2 v^{3}-20 v^{2}\)

45)\(8 u^{6}+34 u^{5}+30 u^{4}\)

Contestar: \(2 u^{4}(4 u+5)(u+3)\)

46)\(4 a^{4}+29 a^{3}+30 a^{2}\)

47)\(12 a^{4} c^{4}-35 a^{3} c^{5}+25 a^{2} c^{6}\)

Contestar: \(a^{2} c^{A}(4 a-5 c)(3 a-5 c)\)

48)\(18 x^{6} z^{5}-39 x^{5} z^{6}+18 x^{4} z^{7}\)

En los Ejercicios 49-56, factorizar completamente cada uno de los polinomios dados.

49)\(12 y^{5}+15 y^{4}-108 y^{3}-135 y^{2}\)

Contestar: \(3 y^{2}(y+3)(y-3)(4 y+5)\)

50)\(9 b^{8}+12 b^{7}-324 b^{6}-432 b^{5}\)

51)\(9 x^{6} z^{5}+6 x^{5} z^{6}-144 x^{4} z^{7}-96 x^{3} z^{8}\)

Contestar: \(3 x^{3} z^{5}(x+4 z)(x-4 z)(3 x+2 z)\)

52)\(12 u^{7} w^{3}+9 u^{6} w^{4}-432 u^{5} w^{5}-324 u^{4} w^{6}\)

53)\(72 z^{6}+108 z^{5}-2 z^{4}-3 z^{3}\)

Contestar: \(z^{3}(6 z+1)(6 z-1)(2 z+3)\)

54)\(216 x^{7}+324 x^{6}-6 x^{5}-9 x^{4}\)

55)\(144 a^{6} c^{3}+360 a^{5} c^{4}-4 a^{4} c^{5}-10 a^{3} c^{6}\)

Contestar: \(2 a^{3} c^{3}(6 a+c)(6 a-c)(2 a+5 c)\)

56)\(48 a^{8} c^{4}+32 a^{7} c^{5}-3 a^{6} c^{6}-2 a^{5} c^{7}\)

En los Ejercicios 57-60, usa tu calculadora para ayudar a factorizar cada uno de los trinomios dados. Siga el esquema del procedimiento en Uso de la Calculadora para Ayudar al\(ac\) Método.

57)\(6 x^{2}+61 x+120\)

Contestar: \((2 x+15)(3 x+8)\)

58)\(16 x^{2}-62 x-45\)

59)\(60 x^{2}-167 x+72\)

Contestar: \((15 x-8)(4 x-9)\)

60)\(28 x^{2}+x-144\)

6.7: Aplicaciones de Factoring

1) Un cuadro rectangular en lienzo mide\(14\) pulgadas por\(36\) pulgadas. El lienzo se monta dentro de un marco de ancho uniforme, aumentando el área total cubierta tanto por la lona como por el marco a pulgadas\(720\) cuadradas. Encuentra el ancho uniforme del marco.

Contestar: \(2\)pulgadas

2) Un cuadro rectangular en lienzo mide\(10\) pulgadas por\(32\) pulgadas. El lienzo se monta dentro de un marco de ancho uniforme, aumentando el área total cubierta tanto por la lona como por el marco a pulgadas\(504\) cuadradas. Encuentra el ancho uniforme del marco.

3) Un proyectil es disparado en ángulo hacia el aire desde lo alto de un clítoris con vista al océano. La distancia del proyectil (en pies) desde la base del cli, viene dada por la ecuación\[x = 180t \nonumber \] y la altura del proyectil sobre el nivel del mar (en pies) viene dada por la ecuación\[y = −16t^2 + 352t + 1664 \nonumber \] donde\(t\) está la cantidad de tiempo (en segundos) que ha pasado desde la liberación del proyectil. ¿Cuánto tiempo pasa antes de que el proyectil salpique en el océano? En ese momento, ¿a qué distancia se encuentra el proyectil de la base del clítoris?

Contestar: \(26\)segundos,\(4,680\) pies

4) Un proyectil es disparado en ángulo hacia el aire desde lo alto de un clítoris con vista al océano. La distancia del proyectil (en pies) desde la base del cli, viene dada por la ecuación\[x = 140t \nonumber \] y la altura del proyectil sobre el nivel del mar (en pies) viene dada por la ecuación\[y = −16t^2 + 288t + 1408 \nonumber \] donde\(t\) está la cantidad de tiempo (en segundos) que ha pasado desde la liberación del proyectil. ¿Cuánto tiempo pasa antes de que el proyectil salpique en el océano? En ese momento, ¿a qué distancia se encuentra el proyectil de la base del clítoris?

5) El producto de dos enteros pares consecutivos es\(624\). Encuentra los enteros.

Contestar: \(-26\)y\(−24\),\(24\) y\(26\)

6) El producto de dos enteros pares consecutivos es\(528\). Encuentra los enteros.

7) El producto de dos enteros positivos consecutivos es\(552\). Encuentra los enteros.

Contestar: \(23\),\(24\)

8) El producto de dos enteros positivos consecutivos es\(756\). Encuentra los enteros.

9) El producto de dos enteros impares consecutivos es\(483\). Encuentra los enteros.

Contestar: \(−23\)y\(−21\),\(21\) y\(23\)

10) El producto de dos enteros impares consecutivos es\(783\). Encuentra los enteros.

11) Un rectángulo tiene\(42\) pies perimetrales y área pies\(104\) cuadrados. Encuentra las dimensiones del rectángulo.

Contestar: \(8\)pies a\(13\) pies

12) Un rectángulo tiene\(32\) pies perimetrales y área de pies\(55\) cuadrados. Encuentra las dimensiones del rectángulo.

13) El radio del círculo exterior es una pulgada más largo que el doble del radio del círculo interno.

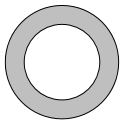
Si el área de la región sombreada es pulgadas\(40\pi \) cuadradas, ¿cuál es la longitud del radio interior?

Contestar: \(3\)pulgadas

14) El radio del círculo exterior es dos pulgadas más largo que tres veces el radio del círculo interno.

Si el área de la región sombreada es pulgadas\(180\pi \) cuadradas, ¿cuál es la longitud del radio interior?

15) Tienes dos números positivos. El segundo número es tres más de dos veces el primer número. La diferencia de sus cuadrados es\(144\). Encuentra ambos números positivos.

Contestar: \(5\)y\(13\)

16) Tienes dos números positivos. El segundo número es dos más de tres veces el primer número. La diferencia de sus cuadrados es\(60\). Encuentra ambos números positivos.

17) Dos números se diferencian por\(5\). La suma de sus cuadrados es\(97\). Encuentra los dos números.

Contestar: \(4\)y\(9\),\(−4\) y\(−9\)

18) Dos números se diferencian por\(6\). La suma de sus cuadrados es\(146\). Encuentra los dos números.

19) La longitud de un rectángulo es tres pies más larga que seis veces su ancho. Si el área del rectángulo es de pies\(165\) cuadrados, ¿cuál es el ancho del rectángulo?

Contestar: \(5\)pies

20) La longitud de un rectángulo es tres pies más larga que nueve veces su ancho. Si el área del rectángulo es de pies\(90\) cuadrados, ¿cuál es el ancho del rectángulo?

21) La relación entre la anchura y la longitud de un rectángulo dado es\(2\) a\(3\), o\(\dfrac {2}{3}\). Si tanto el ancho como el largo se incrementan en\(4\) pulgadas, el área del rectángulo resultante es pulgadas\(80\) cuadradas. Encuentra el ancho y largo del rectángulo original.

Contestar: \(4\)pulgadas por\(6\) pulgadas

22) La relación entre la anchura y la longitud de un rectángulo dado es\(3\) a\(4\), o\(\dfrac {3}{4}\). Si el ancho se incrementa en\(3\) pulgadas y el largo se incrementa en\(6\) pulgadas, el área del rectángulo resultante es pulgadas\(126\) cuadradas. Encuentra el ancho y largo del rectángulo original.