7.2: Notación científica
- Page ID
- 111650
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Comenzamos esta sección examinando poderes de diez.
\[\begin{align*} 10^1 &= 10\\ 10^2 &= 10\cdot 10 = 100\\ 10^3 &= 10\cdot 10\cdot 10 = 1,000\\ 10^4 &= 10\cdot 10\cdot 10\cdot 10 = 10,000 \end{align*} \nonumber \]
Tenga en cuenta que la respuesta para\(10^3\) es un uno seguido de tres ceros. La respuesta para\(10^4\) es un uno seguido de cuatro ceros. ¿Ves el patrón?
Poderes no negativos de diez
En la expresión\(10^n\), el exponente coincide con el número de ceros en la respuesta. De ahí,\(10^n\) será un\(1\) seguido de\(n\) ceros.
Ejemplo\(\PageIndex{1}\)
Simplificar:\(10^9\).
Solución
\(10^9\)debe ser un\(1\) seguido de\(9\) ceros. \[10^9 =1 ,000,000,000 \nonumber \]
Ejercicio\(\PageIndex{1}\)
Simplificar:\(10^6\).
- Contestar
-
\(1,000,000\)
A continuación, examinemos los poderes negativos de diez.
\[\begin{align*} 10^{-1} &= \dfrac{1}{10} = 0.1\\ 10^{-2} &= \dfrac{1}{100} = 0.01\\ 10^{-3} &= \dfrac{1}{1000} = 0.001\\ 10^{-4} &= \dfrac{1}{10000} = 0.0001 \end{align*} \nonumber \]
Tenga en cuenta que la respuesta para\(10^{−3}\) tiene tres decimales y la respuesta para\(10^{−4}\) contiene cuatro decimales.
Poderes negativos de diez
En la expresión\(10^{−n}\), el exponente coincide con el número de decimales en la respuesta. De ahí,\(10^{−n}\) tendrá n decimales, la primera\(n−1\) de las cuales son ceros y el dígito en la enésima posición decimal es a\(1\).
Ejemplo\(\PageIndex{2}\)
Simplificar:\(10^{−7}\).
Solución
\(10^{−7}\)debe tener siete decimales, el primer seis de los cuales son ceros, y el dígito en el séptimo decimal es a\(1\). \[10^{−7} = 0 .0000001 \nonumber \]
Ejercicio\(\PageIndex{2}\)
Simplificar:\(10^{−5}\).
- Contestar
-
\(0.00001\)
Multiplicar números decimales por potencias de diez
Multipliquemos\(1.234567\) por\(10^3\), o equivalentemente, por\(1,000\).
\[\begin{array}{ccc} 1.234567 \\ \;\;\times 1000\\ \hline 1234.567000 \end{array} \nonumber \]
La suma total de dígitos a la derecha del punto decimal en\(1.234567\) y\(1000\) es\(6\). Por lo tanto, colocamos el punto decimal en el producto para que haya seis dígitos a la derecha del punto decimal.
Sin embargo, los ceros finales pueden eliminarse sin cambiar el valor del producto. Es decir, los\(1.234567\) tiempos lo\(1000\) son\(1234.567\). Tenga en cuenta que el punto decimal en el producto está tres lugares más a la derecha que en el factor original. Esta observación lleva al siguiente resultado.
Multiplicando por una potencia no negativa de diez
Multiplicando un número decimal por\(10^n\), donde\(n = 0, 1, 2, 3, \ldots ,\) moverá los\(n\) lugares decimales hacia la derecha.
Ejemplo\(\PageIndex{3}\)
Simplificar:\(325.6783×10^2\).
Solución
Multiplicar por\(10^2\) moverá el punto decimal dos lugares a la derecha. Así:\[325.6783×10^2 = 32,567.83 \nonumber \]
Ejercicio\(\PageIndex{3}\)
Simplificar:\(23.57889×10^3\)
- Contestar
-
\(23,578.89\)
Ejemplo\(\PageIndex{4}\)
Simplificar:\(1.25×10^5\).
Solución
Multiplicar por\(10^5\) moverá el punto decimal dos lugares a la derecha. En este caso, necesitamos sumar ceros al final del número para lograr mover los\(5\) decimales hacia la derecha. \[1.25×105 = 125,000 \nonumber \]
Ejercicio\(\PageIndex{14}\)
Simplificar:\(2.35×10^4\)
- Contestar
-
\(23,500\)
Multipliquemos\(453.9\) por\(10^{−2}\), o equivalentemente, por\(0.01\).
\[\begin{array}{ccc} 453.9 \\ \times 0.01\\ \hline 4.539 \end{array} \nonumber \]
La suma total de dígitos a la derecha del punto decimal en\(453.9\) y\(0.01\) es\(3\). Por lo tanto, colocamos el punto decimal en el producto para que haya\(3\) dígitos a la derecha del punto decimal. Es decir,\(453.9×10^{−2} = 4.539\). Tenga en cuenta que el punto decimal en el producto está dos lugares más a la izquierda que en el factor original. Esta observación lleva al siguiente resultado.
Multiplicando por una potencia negativa de diez
Multiplicando un número decimal por\(10^{−n}\), donde\(n = 1, 2, 3, \ldots ,\) moverá los\(n\) lugares decimales hacia la izquierda.
Ejemplo\(\PageIndex{5}\)
Simplificar:\(14,567.8×10^{−3}\).
Solución
Multiplicar por\(10^{−3}\) moverá el punto decimal tres lugares a la izquierda. Así:\[14,567.8×10^{−3} = 14 .5678 \nonumber \]
Ejercicio\(\PageIndex{5}\)
Simplificar:\(3,854.2×10^{−1}\)
- Contestar
-
\(385 .42\)
Ejemplo\(\PageIndex{6}\)
Simplificar:\(4.3×10^{−4}\).
Solución
Multiplicar por\(10^{−4}\) moverá el punto decimal cuatro lugares hacia la izquierda. En este caso, necesitamos agregar algunos ceros a la izquierda al inicio del número para lograr mover los\(4\) decimales hacia la izquierda. \[4.3×10^{−4} =0.00043\nonumber \]. Observe también el cero a la cabeza antes del punto decimal. Si bien\(.00043\) es un número equivalente, la forma\(0.00043\) es preferida en matemáticas y ciencias.
Ejercicio\(\PageIndex{6}\)
Simplificar:\(2.2×10^{−2}\)
- Contestar
-
\(0.022\)
Formulario de notación científica
Comenzamos por determinar la forma de un número llamado notación científica.
Notación Científica
Un número que tiene la forma\[a×10^b \nonumber \] donde\(b\) es un entero y\(1 ≤| a| < 10\), se dice que está en notación científica.
El requisito\(1 ≤| a| < 10\) dice que la magnitud de un debe ser menor\(1\) y menor que\(10\).
- El número no\(12.34×10^{−4}\) está en notación científica porque\(|12.34| = 12.34\) es mayor que\(10\).
- El número no\(−0.95×10^3\) está en notación científica porque\(|−0.95|= 0.95\) es menor que\(1\).
- El número\(7.58×10^{−12}\) está en notación científica porque\(|7.58|=7.58\) es mayor o igual a\(1\) y menor que\(10\).
- El número\(−1.0×10^{15}\) está en notación científica porque\(|−1.0|=1.0\) es mayor o igual a\(1\) y menor que\(10\).
Después de contemplar estos ejemplos, se deduce que un número en notación científica debe tener exactamente uno de los dígitos\(1, 2, 3, \ldots , 9\) antes del punto decimal. Exactamente uno, ni más, ni menos. Así, cada uno de los siguientes números está en notación científica.
\[4.7×10^8, \quad −3.764×10^{−1}, \quad 3.2×10^0, \quad \text {and} \quad −1.25×10^{−22} \nonumber \]
Colocación de un Número en Notación Científica
Para colocar un número en notación científica, necesitamos mover el punto decimal para que exactamente uno de los dígitos\(1, 2, 3, \ldots , 9\) quede a la izquierda del punto decimal, luego multiplicarlo por la potencia apropiada de para\(10\) que el resultado sea equivalente al número original.
Ejemplo\(\PageIndex{7}\)
Colocar el número\(1,234\) en notación científica.
Solución
Mueve el punto decimal tres lugares a la izquierda para que quede posicionado justo después de la\(1\). Para hacer este nuevo número igual a\(1,234\), multiplicar por\(10^3\). Así:\[1,234 = 1.234×10^3 \nonumber \]
Comprobar: Multiplicar por\(10^3\) mueve los decimales tres lugares a la derecha, entonces:\[1.234×10^3 =1,234 \nonumber \] Este es el número original, por lo que nuestra forma de notación científica es correcta.
Ejercicio\(\PageIndex{7}\)
Colocar el número\(54,321\) en notación científica.
- Contestar
-
\(5 .4321×10^4\)
Ejemplo\(\PageIndex{8}\)
Colocar el número\(0.000025\) en notación científica.
Solución
Mueva el punto decimal cinco lugares a la derecha para que quede posicionado justo después de la\(2\). Para hacer este nuevo número igual a\(0.000025\), multiplicar por\(10^{−5}\). Así:\[0.000025 = 2.5×10^{−5} \nonumber \]
Comprobar: Multiplicar por\(10^{−5}\) mueve los cinco decimales hacia la izquierda, así:\[2.5×10^{−5} = 0 .000025 \nonumber \] Este es el número original, por lo que nuestra forma de notación científica es correcta.
Ejercicio\(\PageIndex{8}\)
Colocar el número\(0.0175\) en notación científica.
- Contestar
-
\(1.75×10^{−2}\)
Ejemplo\(\PageIndex{9}\)
Colocar el número\(34.5×10^{−11}\) en notación científica.
Solución
Primero, mueve el punto decimal un lugar hacia la izquierda para que quede posicionado justo después de los tres. Para hacer esta nueva forma igual a\(34.5\), multiplicar por\(10^1\). \[34.5×10^{−11} = 3.45×10^1×10^{−11} \nonumber \]Ahora, repite la base\(10\) y suma los exponentes.
\[=3 .45×10^{−10} \nonumber \]
Ejercicio\(\PageIndex{9}\)
Colocar el número\(756.98×10^{−5}\) en notación científica.
- Contestar
-
\(7.5698×10^{−3}\)
Ejemplo\(\PageIndex{10}\)
Colocar el número\(0.00093×10^{12}\) en notación científica.
Solución
Primero, mueve el punto decimal cuatro lugares hacia la derecha para que quede posicionado justo después del nueve. Para hacer esta nueva forma igual a\(0.00093\), multiplicar por\(10^{−4}\). \[0.00093×10^{12} = 9.3×10^{−4} ×10^{12} \nonumber \]
Ahora, repite la base\(10\) y suma los exponentes. \[=9.3×10^8 \nonumber \]
Ejercicio\(\PageIndex{10}\)
Colocar el número\(0.00824×10^8\) en notación científica.
- Contestar
-
\(8.24×10^5\)
Notación Científica y Calculadora Gráfica
La calculadora gráfica TI-84 tiene un botón especial para ingresar números en notación científica. Localice la tecla “coma” justo sobre la\(7\) tecla numérica en el teclado de la calculadora (ver Figura\(\PageIndex{1}\)). Justo encima de la tecla “coma”, impresa en la caja de la calculadora está el símbolo EE. Está en el mismo color que la tecla 2, así que tendrás que usar la segunda clave para acceder a este símbolo.

Eso lo sabemos\(2.3 × 10^2 = 230\). Veamos si la calculadora da la misma interpretación.
- Entrar\(2.3\).
- Presiona la segunda tecla, luego la tecla coma. Esto pondrá E en la pantalla de vista de la calculadora.
- Ingrese a\(2\).
- Presione ENTER.

El resultado de estos pasos se muestra en la primera imagen de la Figura\(\PageIndex{2}\). Tenga en cuenta que la calculadora interpreta\(2.3\mathbf{E}2\) como\(2.3×10^2\) y da la respuesta correcta,\(230\). Puede continuar ingresando números en notación científica (ver la imagen del medio en Figura\(\PageIndex{2}\)). Sin embargo, en algún momento los números se vuelven demasiado grandes y la calculadora responde dando salida a los números en notaitón científico. También puede forzar a su calculadora a mostrar números en notación científica en todas las situaciones, presionando primero la tecla MODE, luego seleccionando SCI en la primera línea y presionando la tecla ENTER (vea la tercera imagen en la Figura\(\PageIndex{2}\)). Puede devolver su calculadora al modo “normal” seleccionando NORMAL y presionando la tecla ENTER.
Ejemplo\(\PageIndex{11}\)
Utilice la calculadora gráfica para simplificar:\[(2.35×10^{−12})(3.25×10^{−4}) \nonumber \]
Solución
Primero, tenga en cuenta que podemos aproximarnos\((2.35×10^{−12})(3.25×10^{−4})\) tomando el producto de\(2\) y\(3\) y sumando los poderes de diez.
\[\begin{align*} &(2.35\times 10^{-12})(3.25\times 10^{-4}) \\ &\approx (2\times 10^{-12})(3\times 10^{-4}) \quad \color {Red} \text {Approximate: } 2.35\approx 2 \text { and } 3.25\approx 3 \\ &\approx 6\times 10^{-16} \quad \color {Red} 2\cdot 3 = 6 \text { and } 10^{-12}\cdot 10^{-4} = 10^{-16} \end{align*} \nonumber \]
La calculadora gráfica proporcionará una respuesta precisa. Ingrese\(2.35\mathbf{E}-12\), presione el botón “times”, luego ingrese 3.25E-4 y presione el botón ENTER. Asegúrese de usar el botón “negar” y no el botón “restar” para producir el signo menos. El resultado se muestra en la Figura\(\PageIndex{3}\).

Por lo tanto,\((2.35×10^{−12})(3.25×10^{−4})=7 .6375×10^{−16}\). Tenga en cuenta que esto es bastante cercano a nuestra estimación de\(6 ×10^{−16}\).
Ejercicio\(\PageIndex{11}\)
Utilice la calculadora gráfica para simplificar:\[(3.42×10^6)(5.86×10^{−9}) \nonumber \]
- Contestar
-
\(2.00412×10^{−2}\)
Informar tu respuesta en tu tarea
Después de computar la respuesta a Ejemplo\(\PageIndex{11}\) en tu calculadora, escribe lo siguiente en tu tarea:\[(2.35×10^{−12})(3.25×10^{−4})=7.6375×10^{−16} \nonumber \] No escribas\(7.6375\mathbf{E}-16\).
Ejemplo\(\PageIndex{12}\)
Utilice la calculadora gráfica para simplificar:\[\dfrac{6.1\times 10^{-3}}{(2.7\times 10^4)(1.1\times 10^8)} \nonumber \]
Solución
Nuevamente, no es difícil producir una respuesta aproximada.
\[\begin{align*} &\dfrac{6.1\times 10^{-3}}{(2.7\times 10^4)(1.1\times 10^8)} \\ &\approx \dfrac{6\times 10^{-3}}{(3\times 10^4)(1\times 10^8)} \quad \color {Red} 6.1\approx 6, 2.7\approx 3, \text { and } 1.1\approx 1 \\ &\approx \dfrac{6\times 10^{-3}}{3\times 10^{12}} \quad \color {Red} 3\cdot 1=3 \text { and } 10^{4}\cdot 10^{8} = 10^{12}\\ &\approx \dfrac{6}{3}\cdot \dfrac{10^{-3}}{10^{12}} \quad \color {Red} \dfrac{ac}{bd}=\dfrac{a}{b}\cdot \dfrac{c}{d}\\ &\approx 2\times 10^{-15} \quad \color {Red} \dfrac{6}{3}=2 \text { and } \dfrac{10^{-3}}{10^{12}}=10^{-15} \end{align*} \nonumber\]
Consigamos una respuesta precisa con nuestra calculadora. Ingresa el numerador como\(6.1\mathbf{E}3\), luego presiona el botón “división”. Recuerda que debemos rodear el denominador con paréntesis. Entonces presione la tecla de paréntesis abiertos, luego ingrese\(2.7\mathbf{E}4\). Presiona la tecla “times” y luego ingresa\(1.1\mathbf{E}8\). Presione la tecla Cerrar paréntesis y presione el botón ENTER. El resultado se muestra en la Figura\(\PageIndex{4}\).

Por lo tanto,\(6.1×10^{−3}/(2.7×10^4 ×1.1×10^8)=2 .05387205×10^{−15}\). Tenga en cuenta que esto es bastante cercano a nuestra estimación de\(2×10^{−15}\).
Ejercicio\(\PageIndex{12}\)
Utilice la calculadora gráfica para simplificar:\[\dfrac{2.6\times 10^{4}}{(7.1\times 10^{-2})(6.3\times 10^7)} \nonumber \]
- Responder
-
\(5.8126537×10^{−3}\)
Ejemplo\(\PageIndex{13}\)
La ley universal de la gravitación de Isaac Newton está determinada por la fórmula\[F = \dfrac{GmM}{r^2} \nonumber \] donde\(F\) está la fuerza de atracción entre dos objetos que tienen masa\(m\) y\(M\),\(r\) es la distancia entre los dos objetos, y\(G\) es la constante gravitacional de Newton determinada por:\[G =6 .67428\times 10^{-11} \text {N(m/kg)}^2 \nonumber\] Dado que la masa de la luna es\(7.3477×10^{22}\) kilogramos (kg), la masa de la tierra es\(5.9736×10^{24}\) kilogramos (kg), y la distancia promedio entre la luna y la tierra es\(3.84403×10^8\) metros (m), encontrar la fuerza de atracción entre la tierra y la luna (en newtons (N)).
Solución
Enchufa los números dados en la ley universal de gravitación de Newton.
\[F=\dfrac{GmM}{r^2} \nonumber \]
\[F=\dfrac{(6.673\times 10^{-11})(7.3477\times 10^{22})(5.9736\times 10^{24})}{(3.84403\times 10^8)^2} \nonumber \]
Ingrese la expresión en su calculadora (ver Figura\(\PageIndex{5}\)) como:
\[(6.673\mathbf{E}-11*7.3477\mathbf{E}22*5.9736\mathbf{E}24)/(3.84403\mathbf{E}8)\wedge 2 \nonumber\]
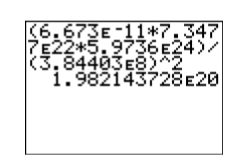
De ahí que la fuerza de atracción entre la tierra y la luna sea aproximadamente\(1.98×10^{20}\) newtons (N).
Ejercicio\(\PageIndex{13}\)
La masa de la Estación Espacial Internacional es\(450,000\) kg, y su distancia promedio al centro de la tierra es\(387,000\) m. Encuentra la fuerza de atracción entre la tierra y la estación (en newtons (N)).
- Responder
-
\(≈ 1.20×109 N\)
Ejemplo\(\PageIndex{14}\)
La estrella más cercana a la tierra es Alpha Centauri, a\(4.37\) años luz de la tierra. Un año luz es la distancia que recorrerá la luz en un año. La velocidad de la luz es de\(186,000\) millas por segundo. ¿A cuántas millas de la tierra hay Alpha Centauri?
Solución
Debido a que la velocidad de la luz se mide en millas por segundo, primero calculemos el número de segundos en\(4.37\) años. Porque hay\(365\) días en un año,\(24\) horas en un día,\(60\) minutos en una hora y\(60\) segundos en un minuto, podemos escribir:
\[\begin{aligned} 4.37 \text {yr} &= 4.37\text {yr}\times 365\dfrac{\text {day}}{\text {yr}}\times 24\dfrac{\text {hr}}{\text {day}}\times 60\dfrac{\text {min}}{\text {hr}}\times 60\dfrac{\text {s}}{\text {min}}\\ &= 4.37{\color {Red}\not {\color {Black}\text {yr}}}\times 365\dfrac{\color {Red}\not {\color {Black}\text {day}}}{\color {Red}\not {\color {Black}\text {yr}}}\times 24\dfrac{\color {Red}\not {\color {Black}\text {hr}}}{\color {Red} \not {\color {Black}\text {day}}}\times 60\dfrac{\color {Red}\not {\color {Black}\text {min}}}{\color {Red}\not {\color {Black}\text {hr}}}\times 60\dfrac{\text {s}}{\color {Red}\not {\color {Black}\text {min}}} \end {aligned} \nonumber \]
Observe cómo cancelan las unidades, indicando que la respuesta final es en segundos. Con nuestro modo de calculadora ajustado a notación científica (ver la imagen de la derecha en la Figura\(\PageIndex{2}\)), multiplicamos los números para obtener el resultado que se muestra en la Figura\(\PageIndex{6}\). Redondeo, el número de segundos en\(4.37\) años es aproximadamente\(1.38 × 10^8\) segundos.
A continuación, calculamos la distancia que recorre la luz en\(4.37\) años. Utilizando el hecho de que la distancia recorrida es igual a la velocidad multiplicada por el tiempo recorrido, tenemos:
\[\begin{aligned} \text {Distance} &= \text {Speed}\times \text {Time}\\ &= 1.86\times 10^5\dfrac{\text {mi}}{\text {s}}\cdot 1.38\times 10^8\text {s}\\ &= 1.86\times 10^5\dfrac{\text {mi}}{\color {Red}\not {\color {Black}\text {s}}}\cdot 1.38\times 10^8 {\color {Red}\not {\color {Black}\text {s}}} \end {aligned} \nonumber\]
Observe cómo cancelan las unidades, indicando que nuestra respuesta es en millas. Nuevamente, con nuestra calculadora establecida en modo de notación científica, calculamos el producto de\(1.86×10^5\) y\(1.38×10^8\). El resultado se muestra en la imagen de la derecha en la Figura\(\PageIndex{6}\).
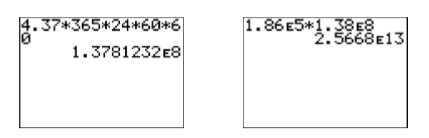
Así, la estrella Alfa Centauri se encuentra aproximadamente\(2.5668×10^{13}\) a millas de la tierra, o se\[2.5668×10^{13} \text {miles} ≈ 25,668,000,000,000 \text {miles} \nonumber \] pronuncia “veinte cuatrillones, seiscientos sesenta y ocho billones de millas”.
Ejercicio\(\PageIndex{14}\)
La estrella Sirio está a\(8.58\) años luz de la tierra. ¿A cuántas millas de la tierra está Sirio?
- Responder
-
\(≈ 5.2425×10^{13}\)millas


