7.3: Simplificar expresiones racionales

Última actualización
Guardar como PDF

Page ID: 111644

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Cada vez que divides un polinomio por un segundo polinomio, formas lo que es, encontrarás ese material bastante útil para esta sección. conocida como expresión racional.

Nota

Se recomienda encarecidamente a los lectores que revisen el material sobre fracciones presentado en la Sección 3 del Capítulo 1.

Expresión racional

La expresión\[\dfrac{p(x)}{q(x)} \nonumber\] donde$p(x)$ y$q(x)$ son polinomios, se denomina expresión racional.

Por ejemplo, cada una de las siguientes es una expresión racional.

$\dfrac{x+2}{3x}$
$\dfrac{x+3}{x^2-2x-4}$
$\dfrac{2x}{3y^2}$

En el ejemplo a), la expresión racional se compone de un binomio sobre un monomio. El ejemplo b) se construye dividiendo un binomio por un trinomio. El ejemplo c) está compuesto por un monomio sobre un monomio, el tipo de expresión racional que más atención ganará en esta sección.

Multiplicar y dividir expresiones racionales

Nos concentraremos en expresiones racionales con numeradores y denominadores monomiales. Recordemos que para formar el producto de dos números racionales, simplemente multiplicamos numeradores y denominadores. La misma técnica se utiliza para multiplicar dos expresiones racionales cualesquiera.

Multiplicar expresiones racionales

Dado$a/b$ y$c/d$, su producto se define como:\[\dfrac{a}{b}\cdot \dfrac{c}{d}=\dfrac{ac}{bd} \nonumber \]

Recuerda, solo necesitas multiplicar numeradores y denominadores. Por ejemplo:

$\dfrac{x}{3}\cdot \dfrac{2}{y} = \dfrac{2x}{3y}$
$\dfrac{2a}{3b^2}\cdot \dfrac{5a}{9b^3} = \dfrac{10a^2}{27b^5}$
$\dfrac{x}{2y}\cdot \left (-\dfrac{3x}{4y^2} \right ) = -\dfrac{3x^2}{8y^3}$

Por supuesto, como muestra el siguiente ejemplo, a veces también necesitas reducir tu respuesta a los términos más bajos.

Ejemplo$\PageIndex{1}$

Simplificar:$\dfrac{2}{x}\cdot \dfrac{x^2}{4}$.

Solución

Multiplicar numeradores y denominadores.

\[\dfrac{2}{x}\cdot \dfrac{x^2}{4} = \dfrac{2x^5}{4x^3} \nonumber \]

Ahora, hay varias formas diferentes de reducir esta respuesta a los términos más bajos, dos de los cuales se muestran a continuación.

Puedes factorizar numerador y denominador, luego cancelar factores comunes. \[\begin{align*} \dfrac{2x^5}{4x^3}&= \dfrac{2\cdot x\cdot x\cdot x\cdot x\cdot x}{2\cdot 2\cdot x\cdot x\cdot x}\\ &= \dfrac{\not{2}\cdot \not {x}\cdot \not{x}\cdot \not{x}\cdot x\cdot x}{\not{2}\cdot 2\cdot \not{x}\cdot \not{x}\cdot \not{x}}\\ &= \dfrac{x^2}{2} \end{align*} \nonumber\]

O puedes escribir la respuesta como un producto, repetir la base y restar exponentes. \[\begin{align*} \dfrac{2x^5}{4x^3}&= \dfrac{2}{4}\cdot \dfrac{x^5}{x^3} \\ &= \dfrac{1}{2}\cdot x^{5-3} \\ &= \dfrac{1}{2}x^2 \end{align*} \nonumber \]

Como dividir por$2$ es lo mismo que multiplicar por$1/2$, estas respuestas son equivalentes. Además, tenga en cuenta que el método de la derecha es más eficiente

Ejercicio$\PageIndex{1}$

Simplemente:$\dfrac{9}{x^2}\cdot \dfrac{x}{6}$.

Responder: $\dfrac{3}{2x}$

Recordemos que al dividir fracciones, invertimos la segunda fracción y multiplicamos.

Dividir expresiones racionales

Dado a/b y c/d, su cociente se define como:\[\begin{align*} \dfrac{a}{b}\div \dfrac{c}{d} &= \dfrac{a}{b}\cdot \dfrac{d}{c}\\ &= \dfrac{ad}{bc} \end{align*}\nonumber\]

Ejemplo$\PageIndex{2}$

Simplificar:$\dfrac{x^2}{y}\div \dfrac{x^4}{2y^2}$.

Solución

Invertir, luego multiplicar.

\[\begin{align*} \dfrac{x^2}{y}\div \dfrac{x^4}{2y^2} &= \dfrac{x^2}{y}\cdot \dfrac{2y^2}{x^4}\\ &= \dfrac{2x^2y^2}{x^4y} \end{align*} \nonumber \]

Ahora, hay varias formas diferentes de reducir esta respuesta a los términos más bajos, dos de los cuales se muestran a continuación.

Puedes factorizar numerador y denominador, luego cancelar factores comunes. \[\begin{align*} \dfrac{2x^2y^2}{x^4y}&= \dfrac{2\cdot x\cdot x\cdot y\cdot y}{x\cdot x\cdot x\cdot x\cdot y}\\ &= \dfrac{2\cdot \not{x}\cdot \not{x}\cdot \not{y}\cdot y}{\not{x}\cdot \not{x}\cdot x\cdot x\cdot \not{y}}\\ &= \dfrac{2y}{x^2} \end{align*} \nonumber\]

O puedes escribir la respuesta como un producto, repetir la base y restar exponentes. \[\begin{align*} \dfrac{2x^2y^2}{x^4y}&= 2\cdot \dfrac{x^2}{x^4}\cdot \dfrac{y^2}{y^1}\\ &= 2x^{-2}y^1\\ &= \dfrac{2y}{x^2} \end{align*} \nonumber\]En el último paso,$x^{−2}$ es lo mismo que$1/x^2$, luego multiplicamos numeradores y denominadores.

Tenga en cuenta que el método de la derecha es más eficiente.

Ejercicio$\PageIndex{2}$

Simplificar:$\dfrac{3y}{x^3}\div \dfrac{y^2}{4x}$.

Responder: $\dfrac{12}{x^2y}$

Sumando y restando expresiones racionales

Primero, recordar las reglas para sumar o restar fracciones que tengan un denominador “común”.

Agregar expresiones racionales

Dado$a/c$ y$b/c$, su suma se define como: Es\[\dfrac{a}{c} + \dfrac{b}{c}=\dfrac{a+b}{c} \nonumber\] decir, sumar los numeradores y colocar el resultado sobre el denominador común.

Los siguientes ejemplos comparten cada uno un denominador común. Agregamos los numeradores, luego colocamos el resultado sobre el denominador común.

\[\dfrac{5}{7}+\dfrac{1}{7}=\dfrac{6}{7},\quad \dfrac{2}{x}+\dfrac{3}{x}=\dfrac{5}{x}, \quad \text {and} \quad \dfrac{x}{y}+\dfrac{3y}{y}=\dfrac{x+3y}{y} \nonumber\]

Ejemplo$\PageIndex{3}$

Simplificar:$\dfrac{3x}{xy}+\dfrac{2y}{xy} \nonumber$.

Solución

Sumar los numeradores, colocando el resultado sobre el denominador común.

\[\dfrac{3x}{xy}+\dfrac{2y}{xy} = \dfrac{3x+2y}{xy} \nonumber\]

Ejercicio$\PageIndex{3}$

Simplificar:$\dfrac{4x}{x^2y}+\dfrac{5y^2}{x^2y}$

Responder: $\dfrac{4x+5y^2}{x^2y}$

Restar expresiones racionales

Dado$a/c$ y$b/c$, su diferencia se define como: Es\[\dfrac{a}{c} - \dfrac{b}{c}=\dfrac{a-b}{c} \nonumber\] decir, restar los numeradores y colocar el resultado sobre el denominador común.

Los siguientes ejemplos comparten cada uno un denominador común. Restamos los numeradores, luego colocamos el resultado sobre el denominador común.

\[\dfrac{7}{9}-\dfrac{2}{9}=\dfrac{2}{9},\quad \dfrac{5a}{b}-\dfrac{3a}{b}=\dfrac{2a}{b}, \quad \text {and} \quad \dfrac{3x}{xy}-\dfrac{5y}{xy}=\dfrac{3x-5y}{xy} \nonumber\]

Como muestra el siguiente ejemplo, a veces es posible que tengas que reducir tu respuesta a los términos más bajos.

Ejemplo$\PageIndex{4}$

Simplificar:$\dfrac{5xy}{2z}-\dfrac{3xy}{2z}$.

Solución

Restar los numeradores, colocando el resultado sobre el denominador común.

\[\begin{align*} \dfrac{5xy}{2z}-\dfrac{3xy}{2z} &= \dfrac{5xy-3xy}{2z}\\ &= \dfrac{2xy}{2z} \end{align*} \nonumber \]

Para reducir a términos más bajos, divida tanto el numerador como el denominador por$2$.

\[\dfrac{xy}{z} \nonumber \]

Ejercicio$\PageIndex{4}$

Simplificar:$\dfrac{8x}{3yz^2}-\dfrac{2x}{3yz^2}$.

Responder: $\dfrac{2x}{yz^2}$

El mínimo denominador común

Al sumar o restar, si las expresiones racionales no comparten un denominador común, primero se deben hacer fracciones equivalentes con un denominador común.

Mínimo común denominador

Si las fracciones$a/b$ y$c/d$ no comparten un denominador común, entonces el mínimo denominador común para$b$ y$d$ se define como el número (o expresión) más pequeño divisible por ambos$b$ y$d$. En símbolos,$\mathrm{LCD}(b,d)$ representa el mínimo común denominador de$b$ y$d$.

Ejemplo$\PageIndex{5}$

Simplificar:$\dfrac{x}{6}+\dfrac{2x}{9}$.

Solución

El número más pequeño divisible por ambos$6$ y$9$ es$18$; es decir,$\mathrm{LCD}(6,9) = 18$. Primero debemos hacer fracciones equivalentes con un denominador común de$18$.

\[\begin{align*} \dfrac{x}{6}+\dfrac{2x}{9} &= \dfrac{x}{6}\cdot {\color {Red}\dfrac{3}{3}}+\dfrac{2x}{9}\cdot {\color {Red}\dfrac{2}{2}}\\ &= \dfrac{3x}{18}+\dfrac{4x}{18} \end{align*} \nonumber \]

\[=\dfrac{7x}{18} \nonumber \]

Ejercicio$\PageIndex{5}$

Simplificar:$\dfrac{3x}{8}+\dfrac{5x}{6}$.

Responder: $\dfrac{29x}{24}$

Ejemplo$\PageIndex{6}$

Simplificar:$\dfrac{y}{8x}-\dfrac{y}{12x}$.

Solución

La expresión más pequeña divisible por ambos$8x$ y$12x$ es$24x$; i.e$\mathrm{LCD}(8x,12x) = 24x$.,. Primero debemos hacer fracciones equivalentes con un denominador común de$24x$, luego colocar la diferencia de los numeradores sobre el denominador común.

\[\begin{align*} \dfrac{y}{8x}-\dfrac{y}{12x} &= \dfrac{y}{8x}\cdot {\color {Red}\dfrac{3}{3}}-\dfrac{y}{12x}\cdot {\color {Red}\dfrac{2}{2}}\\ &= \dfrac{3y}{24x}-\dfrac{2y}{24x}\\ &= \dfrac{y}{24x} \end{align*} \nonumber\]

Ejercicio$\PageIndex{6}$

Simplificar:$\dfrac{x}{8y}-\dfrac{x}{10y}$.

Responder: $\dfrac{x}{40y}$

En Ejemplo$\PageIndex{5}$, no era despreciable imaginar el número más pequeño divisible por ambos$6$ y$9$. Una declaración similar podría aplicarse a Ejemplo$\PageIndex{6}$. Este no es el caso en todas las situaciones.

Ejemplo$\PageIndex{7}$

Simplificar:$\dfrac{5y}{72}-\dfrac{y}{108}$.

Solución

En este ejemplo, no es fácil conjurar el número más pequeño divisible por ambos$72$ y$108$. Como veremos, la factorización prime vendrá al rescate.

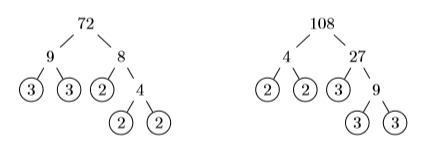
$fig 7.3.a.png$

Así,$72 = 2^3\cdot 3^2$ y$108 = 2^2\cdot 3^3$.

Nota: Procedimiento para determinar el mínimo denominador común (LCD)

Para encontrar el mínimo denominador común para dos o más fracciones, proceda de la siguiente manera:

Factor primo cada denominador, poniendo sus respuestas en forma exponencial.
Para determinar el$\mathrm{LCD}$, anote cada factor que aparezca en tus factorizaciones prime al máximo poder que aparezca.

Siguiendo el procedimiento anterior, enumeramos la factorización prima de cada denominador en forma exponencial. El poder más alto de$2$ lo que aparece es$2^3$. El poder más alto de$3$ lo que aparece es$3^3$.

\[\begin{align*} 72 &= 2^3\cdot 3^2 \quad \color {Red} \text {Prime factor } 72.\\ 108 &= 2^2\cdot 3^3 \quad \color {Red} \text {Prime factor } 108.\\ \mathrm{LCD} &= 2^3\cdot 3^3 \quad \color {Red} \text {Highest power of } 2 \text { is } 2^3. \text { Highest power of } 3 \text { is } 3^3. \end{align*} \nonumber\]

Por lo tanto, el$\mathrm{LCD}$ es$2^3\cdot 3^3 = 8\cdot 27$ o$216$. Por lo tanto:

\[\begin{align*} \dfrac{5y}{72}-\dfrac{y}{108} &= \dfrac{5y}{72}\cdot {\color {Red}\dfrac{3}{3}}-\dfrac{y}{108}\cdot {\color {Red}\dfrac{2}{2}} \quad \color {Red} \text {Make equivalent fractions.} \\ &= \dfrac{15y}{216}-\dfrac{2y}{216} \quad \color {Red} \text {Simplify.} \\ &= \dfrac{13y}{216} \quad \color {Red} \text {Subtract numerators.} \end{align*} \nonumber\]

Ejercicio$\PageIndex{7}$

Simplificar:$\dfrac{7x}{36}-\dfrac{3x}{40}$.

Responder: $\dfrac{43x}{360}$

Ejemplo$\PageIndex{8}$

Simplificar:$\dfrac{7}{15xy^2}-\dfrac{11}{20x^2}$

Solución

Factor primo cada denominador, colocando los resultados en forma exponencial.

\[\begin{align*} 15xy^2 &= 3\cdot 5\cdot x\cdot y^2 \\ 20x^2 &= 2^2 \cdot 5\cdot x^2 \end{align*} \nonumber \]

Para encontrar el$\mathrm{LCD} $, enumerar cada factor que aparece a la mayor potencia que aparece.

\[\mathrm{LCD} = 2^2\cdot 3\cdot 5\cdot x^2 \cdot y^2 \nonumber \]

Simplificar.

\[\mathrm{LCD} = 60 x^2 y^2 \nonumber \]

Después de hacer fracciones equivalentes, coloque la diferencia de los numeradores sobre este denominador común.

\[\begin{align*} \dfrac{7}{15xy^2}-\dfrac{11}{20x^2} &= \dfrac{7}{15xy^2}\cdot {\color {Red}\dfrac{4x}{4x}}-\dfrac{11}{20x^2}\cdot {\color {Red}\dfrac{3y^2}{3y^2}}\\ &= \dfrac{28x}{60x^2y^2}-\dfrac{33y^2}{60x^2y^2}\\ &= \dfrac{28x-33y^2}{60x^2y^2} \end{align*} \nonumber \]

Ejercicio$\PageIndex{8}$

Simplificar:$\dfrac{11}{18xy^2}+\dfrac{7x}{30xy}$

Responder: $\dfrac{55+21x^2}{90x^2y}$

Dividiendo un polinomio por un monomio

Sabemos que la multiplicación es distributiva con respecto a la suma; es decir,$a(b + c)=ab + ac$. Utilizamos esta propiedad para realizar multiplicaciones como:\[x^2(2x^2 −3x−8) = 2x^4 −3x^3 −8x^2 \nonumber \] Sin embargo, también es cierto que la división es distributiva con respecto a la suma.

Propiedad distributiva para división

Si$a$,$b$, y$c$ son números, entonces:\[\dfrac{a+b}{c} = \dfrac{a}{c}+\dfrac{b}{c} \nonumber \]

Por ejemplo, tenga en cuenta que\[\dfrac{4+6}{2} = \dfrac{4}{2}+\dfrac{6}{2} \nonumber \]

Esta forma de la propiedad distributiva se puede utilizar para dividir un polinomio por un monomio.

Ejemplo$\PageIndex{9}$

Dividir$x^2 −2x−3$ por$x^2$.

Solución

Utilizamos la propiedad distributiva, dividiendo cada término por$x^2$.

\[\dfrac{x^2-2x-3}{x^2} = \dfrac{x^2}{x^2}-\dfrac{2x}{x^2}-\dfrac{3}{x^2} \nonumber \]

Ahora reducimos cada término del último resultado a términos más bajos, cancelando factores comunes.

\[= 1-\dfrac{2}{x}-\dfrac{3}{x^2} \nonumber \]

Ejercicio$\PageIndex{9}$

Dividir$9x^3+8x^2−6x$ por$3x^2$.

Responder: $3x+\dfrac{8}{3}-\dfrac{2}{x}$

Ejemplo$\PageIndex{10}$

Dividir$2x^3 −3x + 12$ por$6x^3$.

Solución

Utilizamos la propiedad distributiva, dividiendo cada término por$6x^3$.

\[\dfrac{2x^3-3x+12}{6x^3} = \dfrac{2x^3}{6x^3}-\dfrac{3x}{6x^3}+\dfrac{12}{6x^3} \nonumber\]

Ahora reducimos cada término del último resultado a términos más bajos, cancelando factores comunes.

\[= \dfrac{1}{3}-\dfrac{1}{2x^2}+\dfrac{2}{x^3} \nonumber\]

Ejercicio$\PageIndex{10}$

Dividir$−4x^2 +6x−9$ por$2x^4$.

Responder: $-\dfrac{2}{x^2}+\dfrac{3}{x^3}-\dfrac{9}{x^4}$

Search

Text Color

Text Size

Margin Size

Font Type