8.E: Funciones cuadráticas (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 111655

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

8.1: Introducción a la notación radical

1) Listar todas las raíces cuadradas reales de$-400$.

Contestar: No hay raíces cuadradas reales.

2) Listar todas las raíces cuadradas reales de$64$.

3) Listar todas las raíces cuadradas reales de$-25$.

Contestar: No hay raíces cuadradas reales.

4) Listar todas las raíces cuadradas reales de$81$.

5) Listar todas las raíces cuadradas reales de$49$.

Contestar: $-7,7$

6) Listar todas las raíces cuadradas reales de$-100$.

7) Listar todas las raíces cuadradas reales de$324$.

Contestar: $-18,18$

8) Listar todas las raíces cuadradas reales de$36$.

9) Listar todas las raíces cuadradas reales de$-225$.

Contestar: No hay raíces cuadradas reales.

10) Listar todas las raíces cuadradas reales de$0$.

11) Listar todas las soluciones reales de$x^2 = -225$.

Contestar: No hay soluciones reales.

12) Listar todas las soluciones reales de$x^2 = -25$.

13) Listar todas las soluciones reales de$x^2 = 361$.

Contestar: $-19,19$

14) Listar todas las soluciones reales de$x^2 = 256$.

15) Listar todas las soluciones reales de$x^2 = -400$.

Contestar: No hay soluciones reales.

16) Listar todas las soluciones reales de$x^2 = 0$.

17) Listar todas las soluciones reales de$x^2 = 169$.

Contestar: $-13,13$

18) Listar todas las soluciones reales de$x^{2}=-100$.

19) Listar todas las soluciones reales de$x^{2}=625$.

Contestar: $-25,25$

20) Listar todas las soluciones reales de$x^{2}=324$.

En los Ejercicios 21-30, simplifique cada una de las expresiones dadas.

21)$\sqrt{64}$

Contestar: $8$

22)$-\sqrt{-529}$

23)$-\sqrt{-256}$

Contestar: La expresión no es un número real.

24)$\sqrt{-529}$

25)$-\sqrt{361}$

Contestar: $-19$

26)$\sqrt{-361}$

27)$-\sqrt{100}$

Contestar: $-10$

28)$-\sqrt{196}$

29)$\sqrt{441}$

Contestar: $21$

30)$\sqrt{49}$

En los Ejercicios 31-38, simplifique cada una de las expresiones dadas.

31)$(-\sqrt{17})^{2}$

Contestar: $17$

32)$(-\sqrt{31})^{2}$

33)$(\sqrt{59})^{2}$

Contestar: $59$

34)$(\sqrt{43})^{2}$

35)$(-\sqrt{29})^{2}$

Contestar: $29$

36)$(-\sqrt{89})^{2}$

37)$(\sqrt{79})^{2}$

Contestar: $79$

38)$(\sqrt{3})^{2}$

En los Ejercicios 39-42, para cada una de las ecuaciones dadas, primero use la utilidad 5:intersect en el menú CALC de la calculadora gráfica para determinar las soluciones. Siga las pautas de envío de la calculadora, como se demuestra en el Ejemplo 8.1.9 al informar de la solución en su trabajo de tarea. Segundo, resuelve la ecuación algebraicamente, luego usa tu calculadora para encontrar aproximaciones de tus respuestas y comparar este segundo conjunto con el primer conjunto de respuestas.

39)$x^{2}=37$

Contestar

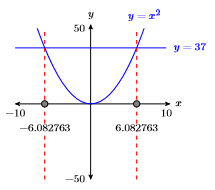
$Respuesta 8.1.39.png$

$\pm \sqrt{37} \approx \pm 6.082763$

40)$x^{2}=32$

41)$x^{2}=11$

Contestar

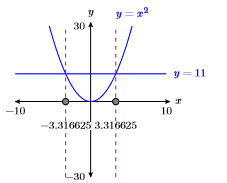
$Respuesta 8.1.41.png$

$\pm \sqrt{11} \approx \pm 3.316625$

42)$x^{2}=42$

8.2: Simplificar expresiones radicales

En los Ejercicios 1-6, simplifica la expresión dada, escribiendo tu respuesta usando un solo símbolo de raíz cuadrada. Consulta el resultado con tu calculadora gráfica.

1)$\sqrt{5} \sqrt{13}$

Contestar: $\sqrt{65}$

2)$\sqrt{2} \sqrt{7}$

3)$\sqrt{17} \sqrt{2}$

Contestar: $\sqrt{34}$

4)$\sqrt{5} \sqrt{11}$

5)$\sqrt{5} \sqrt{17}$

Contestar: $\sqrt{85}$

6)$\sqrt{17} \sqrt{3}$

En los Ejercicios 7-26, convierte cada una de las expresiones dadas en forma radical simple.

7)$\sqrt{56}$

Contestar: $2 \sqrt{14}$

8)$\sqrt{45}$

9)$\sqrt{99}$

Contestar: $3 \sqrt{11}$

10)$\sqrt{75}$

11)$\sqrt{150}$

Contestar: $5 \sqrt{6}$

12)$\sqrt{90}$

13)$\sqrt{40}$

Contestar: $2 \sqrt{10}$

14)$\sqrt{171}$

15)$\sqrt{28}$

Contestar: $2 \sqrt{7}$

16)$\sqrt{175}$

17)$\sqrt{153}$

Contestar: $3 \sqrt{17}$

18)$\sqrt{125}$

19)$\sqrt{50}$

Contestar: $5 \sqrt{2}$

20)$\sqrt{88}$

21)$\sqrt{18}$

Contestar: $3 \sqrt{2}$

22)$\sqrt{117}$

23)$\sqrt{44}$

Contestar: $2 \sqrt{11}$

24)$\sqrt{20}$

25)$\sqrt{104}$

Contestar: $2 \sqrt{26}$

26)$\sqrt{27}$

En los Ejercicios 27-34, encuentra la longitud del lado faltante del triángulo rectángulo. Tu respuesta definitiva debe ser en forma simple y radical.

27)

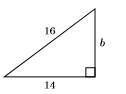
Contestar: $2 \sqrt{15}$

28)

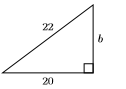
29)

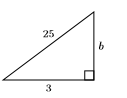
Contestar: $2 \sqrt{154}$

30)

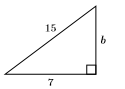
31)

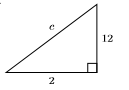
Contestar: $2 \sqrt{37}$

32)

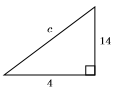
33)

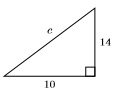
Contestar: $2 \sqrt{74}$

34)

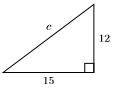
35) En la figura de abajo, se inscribe un triángulo rectángulo en un semicírculo. ¿Cuál es el área de la región sombreada?

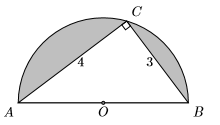
Contestar: $\dfrac{25}{8} \pi-6$

36) En la figura de abajo, se inscribe un triángulo rectángulo en un semicírculo. ¿Cuál es el área de la región sombreada?

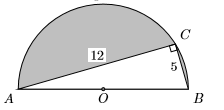
37) La pierna más larga de un triángulo rectángulo es$10$ pies más larga que el doble de la longitud de su pierna más corta. La hipotenusa es$4$ pies más larga que tres veces la longitud de la pierna más corta. Encuentra las longitudes de los tres lados del triángulo rectángulo.

Contestar: $7,24,25$

38) La pierna más larga de un triángulo rectángulo es$2$ pies más larga que el doble de la longitud de su pierna más corta. La hipotenusa es$3$ pies más larga que el doble de la longitud de la pierna más corta. Encuentra las longitudes de los tres lados del triángulo rectángulo.

39) Una escalera de$19$ pies de largo se apoya contra la pared del garaje. Si la base de la escalera está a$5$ pies de la pared del garaje, ¿qué tan alto llega la escalera a la pared del garaje? Usa tu calculadora para redondear tu respuesta a la décima de pie más cercana.

Contestar: $18.3$pies

40) Una escalera de$19$ pies de largo se apoya contra la pared del garaje. Si la base de la escalera está a$6$ pies de la pared del garaje, ¿qué tan alto llega la escalera a la pared del garaje? Usa tu calculadora para redondear tu respuesta a la décima de pie más cercana.

8.3: Completando la Plaza

En los Ejercicios 1-8, encontrar todas las soluciones reales de la ecuación dada. Coloca tus respuestas finales en forma radical simple.

1)$x^{2}=84$

Contestar: $\pm 2 \sqrt{21}$

2)$x^{2}=88$

3)$x^{2}=68$

Contestar: $\pm 2 \sqrt{17}$

4)$x^{2}=112$

5)$x^{2}=-16$

Contestar: Sin soluciones reales

6)$x^{2}=-104$

7)$x^{2}=124$

Contestar: $\pm 2 \sqrt{31}$

8)$x^{2}=148$

En los Ejercicios 9-12, encontrar todas las soluciones reales de la ecuación dada. Coloca tus respuestas finales en forma radical simple.

9)$(x+19)^{2}=36$

Contestar: $-25,-13$

10)$(x-4)^{2}=400$

11)$(x+14)^{2}=100$

Contestar: $-24,-4$

12)$(x-15)^{2}=100$

En los Ejercicios 13-18, cuadrar cada uno de los siguientes binomios.

13)$(x+23)^{2}$

Contestar: $x^{2}+46 x+529$

14)$(x-5)^{2}$

15)$(x+11)^{2}$

Contestar: $x^{2}+22 x+121$

16)$(x-7)^{2}$

17)$(x-25)^{2}$

Contestar: $x^{2}-50 x+625$

18)$(x+4)^{2}$

En Ejercicios 19-24, factorizar cada uno de los siguientes trinomios.

19)$x^{2}+24 x+144$

Respuesta:: $(x+12)^{2}$

20)$x^{2}-16 x+64$

21)$x^{2}-34 x+289$

Respuesta:: $(x-17)^{2}$

22)$x^{2}+8 x+16$

23)$x^{2}-20 x+100$

Respuesta:: $(x-10)^{2}$

24)$x^{2}+16 x+64$

En los Ejercicios 25-36, para cada expresión, completa el cuadrado para formar un trinomio cuadrado perfecto. Comprueba tu respuesta factorizando tu resultado. Asegúrate de revisar tu término medio.

25)$x^{2}-20 x$

Contestar: $x^{2}-20 x+100$

26)$x^{2}-10 x$

27)$x^{2}-6 x$

Contestar: $x^{2}-6 x+9$

28)$x^{2}-40 x$

29)$x^{2}+20 x$

Contestar: $x^{2}+20 x+100$

30)$x^{2}+26 x$

31)$x^{2}+7 x$

Contestar: $x^{2}+7 x+\frac {49}{4}$

32)$x^{2}+19 x$

33)$x^{2}+15 x$

Contestar: $x^{2}+15 x+\frac {225}{4}$

34)$x^{2}+25 x$

35)$x^{2}-5 x$

Contestar: $x^{2}-5 x+\frac {25}{4}$

36)$x^{2}-3 x$

En los Ejercicios 37-52, encontrar todas las soluciones reales, en su caso, de la ecuación dada. Coloca tus respuestas finales en forma radical simple.

37)$x^{2}=18 x-18$

Contestar: $9-3 \sqrt{7}, 9+3 \sqrt{7}$

38)$x^{2}=12 x-18$

39)$x^{2}=16 x-16$

Contestar: $8-4 \sqrt{3}, 8+4 \sqrt{3}$

40)$x^{2}=12 x-4$

41)$x^{2}=-16 x-4$

Contestar: $-8-2 \sqrt{15},-8+2 \sqrt{15}$

42)$x^{2}=-12 x-12$

43)$x^{2}=18 x-9$

Contestar: $9-6 \sqrt{2}, 9+6 \sqrt{2}$

44)$x^{2}=16 x-10$

45)$x^{2}=16 x-8$

Contestar: $8-2 \sqrt{14}, 8+2 \sqrt{14}$

46)$x^{2}=10 x-5$

47)$x^{2}=-18 x-18$

Contestar: $-9-3 \sqrt{7},-9+3 \sqrt{7}$

48)$x^{2}=-10 x-17$

49)$x^{2}=-16 x-20$

Contestar: $-8-2 \sqrt{11},-8+2 \sqrt{11}$

50)$x^{2}=-16 x-12$

51)$x^{2}=-18 x-1$

Contestar: $-9-4 \sqrt{5},-9+4 \sqrt{5}$

52)$x^{2}=-12 x-8$

En los Ejercicios 53-56, resuelve algebraicamente la ecuación dada, declarando tus respuestas finales en forma radical simple. A continuación, utilice la calculadora gráfica para resolver la ecuación, siguiendo la técnica descrita en el Ejemplo 8.3.8. Utilice las Directrices para el envío de la calculadora, como se demuestra en el Ejemplo 8, al reportar la solución en su tarea. Comparar las soluciones determinadas por los dos métodos.

53)$x^{2}-2 x-17=0$

Contestar: $1-3 \sqrt{2}, 1+3 \sqrt{2}$

54)$x^{2}-4 x-14=0$

55)$x^{2}-6 x-3=0$

Contestar: $3-2 \sqrt{3}, 3+2 \sqrt{3}$

56)$x^{2}-4 x-16=0$

8.4: La fórmula cuadrática

En los Ejercicios 1-8, resuelve la ecuación dada factorizando el trinomio usando el$ac$ método -método, luego aplicando la propiedad cero del producto. En segundo lugar, elaborar una segunda solución usando la fórmula cuadrática. Compara tus respuestas.

1)$x^{2}-3 x-28=0$

Contestar: $-4,7$

2)$x^{2}-4 x-12=0$

3)$x^{2}-8 x+15=0$

Contestar: $3,5$

4)$x^{2}-6 x+8=0$

5)$x^{2}-2 x-48=0$

Contestar: $-6,8$

6)$x^{2}+9 x+8=0$

7)$x^{2}+x-30=0$

Contestar: $-6,5$

8)$x^{2}-17 x+72=0$

En los Ejercicios 9-16, usa la fórmula cuadrática para resolver la ecuación dada. Tus respuestas finales deben reducirse a términos más bajos y todas las expresiones radicales deben estar en forma radical simple.

9)$x^{2}-7 x-5=0$

Contestar: $\dfrac{7 \pm \sqrt{69}}{2}$

10)$3 x^{2}-3 x-4=0$

11)$2 x^{2}+x-4=0$

Contestar: $\dfrac{-1 \pm \sqrt{33}}{4}$

12)$2 x^{2}+7 x-3=0$

13)$x^{2}-7 x-4=0$

Contestar: $\dfrac{7 \pm \sqrt{65}}{2}$

14)$x^{2}-5 x+1=0$

15)$4 x^{2}-x-2=0$

Contestar: $\dfrac{1 \pm \sqrt{33}}{8}$

16)$5 x^{2}+x-2=0$

En los Ejercicios 17-24, usa la fórmula cuadrática para resolver la ecuación dada. Tus respuestas finales deben reducirse a términos más bajos y todas las expresiones radicales deben estar en forma radical simple.

17)$x^{2}-x-11=0$

Contestar: $\dfrac{1 \pm 3 \sqrt{5}}{2}$

18)$x^{2}-11 x+19=0$

19)$x^{2}-9 x+9=0$

Contestar: $\dfrac{9 \pm 3 \sqrt{5}}{2}$

20)$x^{2}+5 x-5=0$

21)$x^{2}-3 x-9=0$

Contestar: $\dfrac{3 \pm 3 \sqrt{5}}{2}$

22)$x^{2}-5 x-5=0$

23)$x^{2}-7 x-19=0$

Contestar: $\dfrac{7 \pm 5 \sqrt{5}}{2}$

24)$x^{2}+13 x+4=0$

En los Ejercicios 25-32, usa la fórmula cuadrática para resolver la ecuación dada. Tus respuestas finales deben reducirse a términos más bajos y todas las expresiones radicales deben estar en forma radical simple.

25)$12 x^{2}+10 x-1=0$

Contestar: $\dfrac{-5 \pm \sqrt{37}}{12}$

26)$7 x^{2}+6 x-3=0$

27)$7 x^{2}-10 x+1=0$

Contestar: $\dfrac{5 \pm 3 \sqrt{2}}{7}$

28)$7 x^{2}+4 x-1=0$

29)$2 x^{2}-12 x+3=0$

Contestar: $\dfrac{6 \pm \sqrt{30}}{2}$

30)$2 x^{2}-6 x-13=0$

31)$13 x^{2}-2 x-2=0$

Contestar: $\dfrac{1 \pm 3 \sqrt{3}}{13}$

32)$9 x^{2}-2 x-3=0$

33) Un objeto es lanzado verticalmente y su altura$y$ (en pies) sobre el nivel del suelo viene dada por la ecuación$y = 240 + 160t− 16t^2$, donde$t$ está el tiempo (en segundos) que ha pasado desde su lanzamiento. ¿Cuánto tiempo debe pasar después del lanzamiento antes de que el objeto regrese al nivel del suelo? Después de colocar la respuesta en forma simple y reducir, usa tu calculadora para redondear la respuesta a la décima de segundo más cercana.

Contestar: $11.3$segundos

34) Un objeto es lanzado verticalmente y su altura$y$ (en pies) sobre el nivel del suelo viene dada por la ecuación$y = 192 + 288t− 16t^2$, donde$t$ está el tiempo (en segundos) que ha pasado desde su lanzamiento. ¿Cuánto tiempo debe pasar después del lanzamiento antes de que el objeto regrese al nivel del suelo? Después de colocar la respuesta en forma simple y reducir, usa tu calculadora para redondear la respuesta a la décima de segundo más cercana.

35) Los ingresos de un fabricante$R$ devengados por la venta de$x$ widgets vienen dados por la ecuación$R = 6000x − 5x^2$. Los costos del fabricante para construir$x$ widgets viene dado por la ecuación$C = 500000 + 5.25x$. El punto de equilibrio para el fabricante se determina como el número de widgets construidos y vendidos por lo que los ingresos y costos del fabricante son idénticos. Encuentre la cantidad de widgets requeridos para ser construidos y vendidos para que el fabricante “rompa el par”. Redondee sus respuestas al widget más cercano.

Contestar: $90$widgets,$1109$ widgets

36) Los ingresos de un fabricante$R$ devengados por la venta de$x$ widgets vienen dados por la ecuación$R = 4500x−15.25x^2$. ¿Cuántos widgets se deben vender para que los ingresos del fabricante sean$\$125,000$? Redondee sus respuestas al widget más cercano.

37) Mike se sube a su bicicleta al mediodía y comienza a viajar hacia el norte a un ritmo constante de$6$ millas por hora. A las 2:00pm, Todd se sube a su bicicleta en el mismo punto de partida y comienza a viajar con rumbo este a un ritmo constante de$8$ millas por hora. ¿A qué hora del día estarán a$60$ kilómetros de distancia (como los vuelos de cuervo)? No te preocupes por la forma simple, solo informa la hora del día, correcta al minuto más cercano.

Contestar: 7:12pm

38) Mikaela se sube a su bicicleta al mediodía y comienza a viajar hacia el norte a un ritmo constante de$4$ millas por hora. A la 1:00pm, Rosemarie se sube a su bicicleta en el mismo punto de partida y comienza a viajar hacia el este a un ritmo constante de$6$ millas por hora. ¿A qué hora del día estarán a$20$ kilómetros de distancia (como los vuelos de cuervo)? No te preocupes por la forma simple, solo informa la hora del día, correcta al minuto más cercano.

39) El área de un campo rectangular es de pies$76$ cuadrados. La longitud del campo es$7$ pies más larga que su ancho. Encuentra las dimensiones del campo, correctas a la décima de pie más cercana.

Contestar: $5.9$por$12.9$ pies

40) El área de un campo rectangular es de pies$50$ cuadrados. La longitud del campo es$8$ pies más larga que su ancho. Encuentra las dimensiones del campo, correctas a la décima de pie más cercana.

41) Las concentraciones medias de dióxido de carbono sobre Mauna Loa, Hawaii, son recopiladas por el Laboratorio de Investigación del Sistema Terrestre (ESRL) en conjunto con la Administración Nacional Oceánica y Atmosférica (NOAA). En la siguiente tabla se muestran las concentraciones medias anuales en partes por millón para los años 1962, 1982 y 2002.

Año	1962	1982	2002
Concentración (ppm)	318	341	373

Un modelo cuadrático se ajusta a estos datos, que arroja\[C =0 .01125t^2 +0 .925t+ 318 \nonumber \] dónde$t$ está el número de años desde 1962 y$C$ es la concentración media anual (en partes por millón) de dióxido de carbono sobre Mauna Loa. Utilice el modelo para determinar el año en que la concentración media de dióxido de carbono fue$330$ partes por millón. Redondee su respuesta al año más cercano.

Contestar: 1973

42) La Oficina del Censo de Estados Unidos proporciona datos históricos sobre el número de estadounidenses mayores de$85$.

Año	1970	1990	2010
Población mayor de 85 años (millones)	1.4	3.0	5.7

Un modelo cuadrático se ajusta a estos datos, arrojando\[P =0 .01375t^2 +0 .0525t+1 .4 \nonumber \] dónde$t$ está el número de años desde 1970 y$P$ es el número de estadounidenses (en millones) mayores de la edad de$85$. Utilice el modelo para determinar el año en que el número de estadounidenses mayores de edad$85$ era$2,200,000$. Redondee su respuesta al año más cercano.

Search

Text Color

Text Size

Margin Size

Font Type