8.4: La fórmula cuadrática

Primero comenzamos con la definición de una ecuación cuadrática.

Ecuación cuadrática

Una ecuación polinómica de segundo grado de la forma\[ax^2 + bx + c =0 \nonumber \] donde\(a\),\(b\), y\(c\) son cualquier número real, se denomina ecuación cuadrática en\(x\).

El objetivo de esta sección es desarrollar un atajo formulaico que proporcione soluciones exactas de la ecuación cuadrática ax2 +bx+c = 0. Comenzamos moviendo el término constante al otro lado de la ecuación.

\[\begin{array}{rlrl}{a x^{2}+b x+c} & {=0} & {} & \color{Red} {\text { Quadratic equation. }} \\ {a x^{2}+b x} & {=-c} & {} & \color{Red} {\text { Subtract } c \text { from both sides. }}\end{array} \nonumber \]

En preparación para completar el cuadrado, a continuación dividimos ambos lados de la ecuación por\(a\).

\[x^{2}+\dfrac{b}{a} x=-\dfrac{c}{a} \quad \text { Divide both sides by } a \nonumber \]

Ahora completamos la plaza. Toma la mitad del coecient de\(x\), luego cuadrar el resultado.

\(\dfrac{1}{2} \cdot \dfrac{b}{a}=\dfrac{b}{2 a}\)cuando al cuadrado da\(\left(\dfrac{b}{2 a}\right)^{2}=\dfrac{b^{2}}{4 a^{2}}\)

Ahora sumamos\(\dfrac{b^{2}}{4 a^{2}}\) a ambos lados de la ecuación.

\[x^{2}+\dfrac{b}{a} x+\dfrac{b^{2}}{4 a^{2}}=-\dfrac{c}{a}+\dfrac{b^{2}}{4 a^{2}} \quad \color {Red} \text { Add } b^{2} /\left(4 a^{2}\right) \text { to both sides. } \nonumber \]

A la izquierda, facetamos el trinomio cuadrado perfecto. A la derecha, hacemos fracciones equivalentes con un denominador común.

\[\begin{array}{ll}{\left(x+\dfrac{b}{2 a}\right)^{2}=-\dfrac{c}{a} \cdot \dfrac{4 a}{4 a}+\dfrac{b^{2}}{4 a^{2}}} & \color {Red} {\text { On the left, factor. On the right, }} \\ {} & \color {Red} {\text { create equivalent fractions with }} \\ {\left(x+\dfrac{b}{2 a}\right)^{2}=-\dfrac{4 a c}{4 a^{2}}+\dfrac{b^{2}}{4 a^{2}}} & \color {Red} {\text { Multiply numerators and denominators. }} \\ {\left(x+\dfrac{b}{2 a}\right)^{2}=\dfrac{b^{2}-4 a c}{4 a^{2}}} & \color {Red} {\text { Add fractions. }}\end{array} \nonumber \]

Cuando tomamos la raíz cuadrada, hay dos respuestas.

\[x+\dfrac{b}{2 a}=\pm \sqrt{\dfrac{b^{2}-4 a c}{4 a^{2}}} \quad \color {Red} \text { Two square roots. } \nonumber \]

Cuando tomas la raíz cuadrada de una fracción, tomas la raíz cuadrada tanto del numerador como del denominador.

\[\begin{aligned} x+\dfrac{b}{2 a} &=\pm \dfrac{\sqrt{b^{2}-4 a c}}{\sqrt{4 a^{2}}} \\ x+\dfrac{b}{2 a} &=\pm \dfrac{\sqrt{b^{2}-4 a c}}{2 a} \quad \color {Red} \text { Simplify: } \sqrt{4 a^{2}}=2 a \\ x &=-\dfrac{b}{2 a} \pm \dfrac{\sqrt{b^{2}-4 a c}}{2 a} \quad \color {Red} \text { Subtract } b /(2 a) \text { from both sides } \end{aligned} \nonumber \]

Debido a que ambas fracciones tienen el mismo denominador, podemos sumar y restar numeradores y poner la respuesta sobre el denominador común.

\[x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \]

La fórmula cuadrática

La ecuación\(a x^{2}+b x+c=0\) se denomina ecuación cuadrática. Sus soluciones están dadas por la\[x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \] llamada fórmula cuadrática.

¡Uf! Afortunadamente, ¡el resultado es mucho más fácil de aplicar que de desarrollar! Probemos algunos ejemplos.

Ejemplo\(\PageIndex{1}\)

Resolver para\(x: x^{2}-4 x-5=0\)

Solución

El par entero\(1,−5\) tiene producto\(ac = −5\) y suma\(b = −4\). De ahí que este trinomio faccione.

\[\begin{array}{r}{x^{2}-4 x-5=0} \\ {(x+1)(x-5)=0}\end{array} \nonumber \]

Ahora podemos usar la propiedad cero producto para escribir:

\[\begin{array}{rlrl}{x+1} & {=0} & {\text { or }} & {x-5} & {=0} \\ {x} & {=-1} & {} & {x} & {=5}\end{array} \nonumber \]

Así, las soluciones son\(x =−1\) y\(x = 5\). Ahora, vamos a probar la fórmula cuadrática. Primero, debemos comparar nuestra ecuación con la ecuación cuadrática, luego determinar los valores de\(a\),\(b\), y\(c\).

\[\begin{array}{l}{a x^{2}+b x+c=0} \\ {x^{2}-4 x-5=0}\end{array} \nonumber \]

Comparando ecuaciones, vemos que\(a = 1\),\(b = −4\), y\(c = −5\). Ahora vamos a enchufar estos números en la fórmula cuadrática. Primero, reemplace cada ocurrencia de\(a\),\(b\), y\(c\) en la fórmula cuadrática con paréntesis abiertos.

\ [\ begin {alineado}
x &=\ dfrac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\ quad\ color {Rojo}\ text {La fórmula cuadrática.}\\ x& = {\ dfrac {- (\ quad)\ pm\ sqrt {(\ quad) ^ {2} -4 () ()} {2 ()}}\ quad\ quad\ color {Rojo}\ texto {Reemplazar} a, b,\ texto {y} c\ texto {con paréntesis abiertos.}}\ end {alineado}\ nonumber\]

Ahora podemos sustituir:\(1\) para\(a\),\(−4\) para\(b\), y\(−5\) para\(c\).

\[\begin{array}{ll}{x=\dfrac{-(-4) \pm \sqrt{(-4)^{2}-4(1)(-5)}}{2(1)}} & \color {Red} {\text { Substitute: } 1 \text { for } a,-4 \text { for } b} \\ {x=\dfrac{4 \pm \sqrt{16+20}}{2}} & \color {Red} {\text { Simplify. Exponent first, then }} \\ {x=\dfrac{4 \pm \sqrt{36}}{2}} & \color {Red} {\text { Add: } 16+20=36} \\ {x=\dfrac{4 \pm 6}{2}} & \color {Red} {\text { Simplify: } \sqrt{36}=6}\end{array} \nonumber \]

Tenga en cuenta que debido al símbolo “más o menos”, tenemos dos respuestas.

\[\begin{array}{ll}{x=\dfrac{4-6}{2}} & \text {or} & {x=\dfrac{4+6}{2}} \\ {x=\dfrac{-2}{2}} && {x=\dfrac{10}{2}} \\ {x=-1} && {x=5}\end{array} \nonumber \]

Tenga en cuenta que estas respuestas coinciden con las respuestas encontradas usando la prueba ac para facturar el trinomio.

Ejercicio\(\PageIndex{1}\)

Resolver para\(x: x^{2}-8x+12=0\)

Responder

\(2\),\(6\)

Ejemplo\(\PageIndex{2}\)

Resolver para\(x : x^{2}=5 x+7\)

Solución

La ecuación es no lineal, hacer un lado cero.

\[\begin{array}{rlrl}{x^{2}} & {=5 x+7} & {} & \color {Red} {\text { Original equation. }} \\ {x^{2}-5 x-7} & {=0} & {} & \color {Red} {\text { Nonlinear. Make one side zero. }}\end{array} \nonumber \]

Compare\(x^2 −5x−7 = 0\) con\(ax^2 + bx + c = 0\) y tenga en cuenta que\(a = 1\),\(b = −5\), y\(c = −7\). Reemplazar cada ocurrencia de\(a\),\(b\), y\(c\) con paréntesis abiertos para preparar la fórmula cuadrática para la sustitución.

\[\begin{array}{ll}{x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}} & \color {Red} {\text { The quadratic formula. }} \\ {x=\dfrac{-( ) \pm \sqrt{( )^{2}-4( )( )}}{2( )}} & \color {Red} {\text { Replace } a, b, \text { and } c \text { with }}\end{array} \nonumber \]

Sustituto de\(a\),\(1\)\(−5\) para\(b\), y\(−7\) para\(c\).

\[\begin{array}{ll}{x=\dfrac{-(-5) \pm \sqrt{(-5)^{2}-4(1)(-7)}}{2(1)}} & \color {Red} {\text { Substitute: } a=1, b=-5, c=-7} \\ {x=\dfrac{5 \pm \sqrt{25+28}}{2}} & \color {Red} {\text { Exponents and multiplication first. }} \\ {x=\dfrac{5 \pm \sqrt{53}}{2}} & \color {Red} {\text { Simplify. }}\end{array} \nonumber \]

Consulta: Usa la calculadora para verificar cada solución (ver Figura\(\PageIndex{1}\)). Tenga en cuenta que al almacenar\((5-\sqrt{53}) / 2\) en\(\mathbf{X}\), debemos rodear el numerador entre paréntesis.

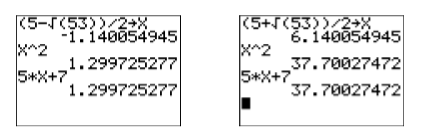
Figura\(\PageIndex{1}\): Cheque\((5-\sqrt{53}) / 2\) y\((5+\sqrt{53}) / 2\).

En cada imagen de la Figura\(\PageIndex{1}\), después de almacenar la solución en\(\mathbf{X}\), tenga en cuenta que los lados izquierdo y derecho de la ecuación original\(x^2 =5 x + 7\) producen el mismo número, verificando que nuestras soluciones son correctas.

Ejercicio\(\PageIndex{2}\)

Resolver para\(x : x^{2}+7 x=10\)

Responder

\((-7+\sqrt{89}) / 2,(-7-\sqrt{89}) / 2\)

Además de colocar todas las raíces cuadradas en forma radical simple, a veces necesitas reducir tu respuesta a los términos más bajos.

Ejemplo\(\PageIndex{3}\)

Resolver para\(x : 7 x^{2}-10 x+1=0\)

Solución

Compare\(7x^2 −10x + 1 = 0\) con\(ax^2 + bx + c = 0\) y tenga en cuenta que\(a = 7\),\(b = −10\), y\(c = 1\). Reemplazar cada ocurrencia de\(a\),\(b\), y\(c\) con paréntesis abiertos para preparar la fórmula cuadrática para la sustitución.

\ [\ begin {alineado}
x &=\ dfrac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\ quad\ color {Rojo}\ text {La fórmula cuadrática.}\\
x &=\ dfrac {- (\ quad)\ pm\ sqrt {() ^ {2} -4 () (quad)}} {2 ()}\\ color {Rojo}\ texto {Reemplazar} a, b,\ texto {y} c\ texto {con paréntesis abiertos.}
\ end {alineado}\ nonumber\]

Sustituto de\(a\),\(7\)\(−10\) para\(b\), y\(1\) para\(c\).

\[\begin{array}{ll}{x=\dfrac{-(-10) \pm \sqrt{(-10)^{2}-4(7)(1)}}{2(7)}} & \color {Red} {\text { Substitute: } 7 \text { for } a} \\ {x=\dfrac{10 \pm \sqrt{100-28}}{14}} & \color {Red} {\text { Exponent, then multiplication. }} \\ {x=\dfrac{10 \pm \sqrt{72}}{14}} & \color {Red} {\text { Simplify. }}\end{array} \nonumber \]

En este caso, tenga en cuenta que podemos facturar un cuadrado perfecto, a saber\(\sqrt{36}\).

\[\begin{array}{ll}{x=\dfrac{10 \pm \sqrt{36} \sqrt{2}}{14}} & \color {Red} {\sqrt{72}=\sqrt{36} \sqrt{2}} \\ {x=\dfrac{10 \pm 6 \sqrt{2}}{14}} & \color {Red} {\text { Simplify: } \sqrt{36}=6}\end{array} \nonumber \]

Por último, observe que tanto el numerador como el denominador son divisibles por\(2\).

\ [\ begin {alineado}
x&=\ dfrac {\ tfrac {10\ pm 6\ sqrt {2}} {2}} {\ tfrac {14} {2}}\ quad\ color {Rojo}\ texto {Divide numerador y denominador por} 2. \\
x&=\ dfrac {\ tfrac {10} {2}\ pm\ tfrac {6\ sqrt {2}} {2}} {\ tfrac {14} {2}}\ quad\ color {Rojo}\ texto {Distribuye el} 2.\ x&=\ dfrac {5\ pm 3\ sqrt {2}} {7}\ quad\ color {Rojo}\ texto {Simplificar.}
\ end {alineado}\ nonumber\]

Simplificación alternativa: En lugar de dividir el numerador y el denominador por\(2\), algunos prefieren factografiar y cancelar, de la siguiente manera.

\[\begin{array}{ll}{x=\dfrac{10 \pm 6 \sqrt{2}}{14}} & \color {Red} {\text { Original answer. }} \\ {x=\dfrac{2(5 \pm 3 \sqrt{2})}{2(7)}} & \color {Red} {\text { Factor out a } 2} \\ {x=\dfrac{\not{2}(5 \pm 3 \sqrt{2})}{\not{2}(7)}} & \color {Red} {\text { Cancel. }} \\ {x=\dfrac{5 \pm 3 \sqrt{2}}{7}} & \color {Red} {\text { Simplify. }}\end{array} \nonumber \]

Tenga en cuenta que obtenemos la misma respuesta usando esta técnica.

Ejercicio\(\PageIndex{3}\)

Resolver para\(x : 3 x^{2}+8 x+2=0\)

Responder

\((-4+\sqrt{10}) / 3,(-4-\sqrt{10}) / 3\)

Ejemplo\(\PageIndex{4}\)

Un objeto es lanzado verticalmente y su altura\(y\) (en pies) sobre el nivel del suelo viene dada por la ecuación\(y = 320+192t−16t^2\), donde está el tiempo (en segundos) que ha pasado desde su lanzamiento. ¿Cuánto tiempo debe pasar después del lanzamiento antes de que el objeto regrese al nivel del suelo? Después de colocar la respuesta en forma simple y reducir, usa tu calculadora para redondear la respuesta a la décima de segundo más cercana.

Solución

Cuando el objeto vuelve al nivel del suelo, su altura\(y\) sobre el nivel del suelo es\(y = 0\) pies. Para encontrar el momento en que esto ocurre, sustituya\(y = 0\) en la fórmula\(y = 320 + 192t−16t^2\) y resuelva para\(t\).

\[\begin{array}{ll}{y=320+192 t-16 t^{2}} & \color {Red} {\text { Original equation. }} \\ {0=320+192 t-16 t^{2}} & \color {Red} {\text { Set } y=0}\end{array} \nonumber \]

Cada uno de los países es divisible por\(−16\).

\[0=t^{2}-12 t-20 \quad \color{Red} \text { Divide both sides by }-16 \nonumber \]

Compare\(t^2−12t−20 = 0\) con\(at^2 +bt+c = 0\) y tenga en cuenta que\(a = 1\),\(b = −12\), y\(c = −20\). Reemplazar cada ocurrencia de\(a\),\(b\), y\(c\) con paréntesis abiertos para preparar la fórmula cuadrática para la sustitución. Tenga en cuenta que estamos resolviendo para t esta vez, no\(x\).

\[\begin{array}{ll}{x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}} & \color {Red} {\text { The quadratic formula. }} \\ {x=\dfrac{-( ) \pm \sqrt{( )^{2}-4( )( )}}{2( )}} & \color {Red} {\text { Replace } a, b, \text { and } c \text { with open parentheses. }}\end{array} \nonumber \]

Sustituto de\(a\),\(1\)\(−12\) para\(b\), y\(−20\) para\(c\).

\[\begin{array}{ll}{t=\dfrac{-(-12) \pm \sqrt{(-12)^{2}-4(1)(-20)}}{2(1)}} & \color {Red} {\text { Substitute: } 1 \text { for } a} \\ {t=\dfrac{12 \pm \sqrt{144+80}}{2}} & \color {Red} {\text { Exponent, then multiplication. }} \\ {t=\dfrac{12 \pm \sqrt{224}}{2}} & \color {Red} {\text { Simplify. }}\end{array} \nonumber \]

La respuesta no está en forma simple, ya que podemos factorial\(\sqrt{16}\).

\[\begin{array}{ll}{t=\dfrac{12 \pm \sqrt{16} \sqrt{14}}{2}} & \color {Red} {\sqrt{224}=\sqrt{16} \sqrt{14}} \\ {t=\dfrac{12 \pm 4 \sqrt{14}}{2}} & \color {Red} {\text { Simplify: } \sqrt{16}=4}\end{array} \nonumber \]

Utilice la propiedad distributiva para dividir ambos términos en el numerador por\(2\).

\[\begin{array}{ll}{t=\dfrac{12}{2} \pm \dfrac{4 \sqrt{14}}{2}} & \color{Red} {\text { Divide both terms by } 2} \\ {t=6 \pm 2 \sqrt{14}} & \color {Red} {\text { Simplify }}\end{array} \nonumber \]

Así, tenemos dos soluciones,\(t=6-2 \sqrt{14}\) y\(t=6+2 \sqrt{14}\). Usa tu calculadora para encontrar aproximaciones decimales y luego redondear a la décima más cercana.

Figura\(\PageIndex{2}\): Uso de la calculadora para encontrar aproximaciones decimales

\[t \approx-1.5,13.5 \nonumber \]

El tiempo negativo es irrelevante, por lo que a la décima de segundo más cercana, le toma al objeto aproximadamente\(13.5\) segundos regresar al nivel del suelo.

Ejercicio\(\PageIndex{4}\)

Un objeto es lanzado verticalmente y su altura\(y\) (en pies) sobre el nivel del suelo viene dada por la ecuación\(y = 160 + 96t−16t^2\), donde\(t\) está el tiempo (en segundos) que ha pasado desde su lanzamiento. ¿Cuánto tiempo debe pasar después del lanzamiento antes de que el objeto regrese al nivel del suelo?

Responder

\(3+\sqrt{19} \approx 7.4\)segundos

Ejemplo\(\PageIndex{5}\)

Arnie se sube a su bicicleta al mediodía y comienza a viajar hacia el norte a un ritmo constante de\(12\) millas por hora. A la 1:00 P M, Bárbara se sube a su bicicleta en el mismo punto de partida y comienza a andar con rumbo este a un ritmo constante de\(8\) millas por hora. ¿A qué hora del día estarán a\(50\) kilómetros de distancia (como los vuelos de cuervo)? No te preocupes por la forma simple, solo informa la hora del día, correcta al minuto más cercano.

Solución

Por el momento están a\(50\) kilómetros de distancia, dejemos\(t\) representar el tiempo que Arnie lleva montando desde el mediodía. Debido a que Bárbara comenzó a la 1:00 P M, lleva una hora cabalgando menos que Arnie. Entonces,\(t−1\) representemos los números de horas que Bárbara ha estado montando en el momento en que están\(50\) a kilómetros de distancia.

Ahora bien, si Arnie ha estado montando a un ritmo constante de\(12\) millas por hora durante\(t\) horas, entonces ha recorrido una distancia de\(12t\) millas. Debido a que Bárbara ha estado montando a un ritmo constante de\(8\) millas por hora\(t−1\) durante horas, ha recorrido una distancia de\(8(t−1)\) millas.

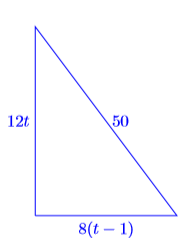
Figura\(\PageIndex{3}\):\(50\) kilómetros de distancia.

La distancia y dirección recorrida por Arnie y Barbara están señaladas en la Figura\(\PageIndex{3}\). Tenga en cuenta que tenemos un triángulo rectángulo, por lo que los lados del triángulo deben satisfacer el Teorema de Pitágoras. Es decir,

\[(12 t)^{2}+[8(t-1)]^{2}=50^{2} \quad \color{Red} \text { Use the Pythagorean Theorem. } \nonumber \]

Distribuir el\(8\).

\[(12 t)^{2}+(8 t-8)^{2}=50^{2} \quad \color{Red} \text { Distribute the } 8 \nonumber \]

Cuadrar cada término. \((a−b)^2 = a^2 −2ab + b^2\)Úselo para expandir\((8t−8)^2\).

\[\begin{aligned} 144 t^{2}+64 t^{2}-128 t+64 &=2500 \quad \color{Red} \text { Square each term. } \\ 208 t^{2}-128 t+64 &=2500 \quad \color{Red} \text { Simplify: } 144 t^{2}+64 t^{2}=208 t^{2} \end{aligned} \nonumber \]

La ecuación resultante es no lineal. Hacer un lado igual a cero.

\[\begin{array}{rlrl}{208 t^{2}-128 t-2436} & {=0} & {} & \color{Red} {\text { Subtract } 2500 \text { from both sides. }} \\ {52 t^{2}-32 t-609} & {=0} & {} & \color{Red} {\text { Divide both sides by } 4 .}\end{array} \nonumber \]

Compare\(52t^2 −32t−609 = 0\) con\(at^2 + bt + c = 0\) y tenga en cuenta que\(a = 52\),\(b = −32\), y\(c = −609\). Reemplazar cada ocurrencia de\(a\),\(b\), y\(c\) con paréntesis abiertos para preparar la fórmula cuadrática para la sustitución. Tenga en cuenta que estamos resolviendo para\(t\) este momento, no\(x\).

\[\begin{array}{ll}{x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}} & \color{Red} {\text { The quadratic formula. }} \\ {x=\dfrac{-( ) \pm \sqrt{( )^{2}-4( )( )}}{2( )}} & \color{Red} {\text { Replace } a, b, \text { and } c \text { with }}\end{array} \nonumber \]

Sustituto de\(a\),\(52\)\(−32\) para\(b\), y\(−609\) para\(c\).

\[\begin{align*} t &= \dfrac{-(-32) \pm \sqrt{(-32)^{2}-4(52)(-609)}}{2(52)} \quad \color {Red} \text { Substitute: } 52 \text { for } a\\ t &= \dfrac{32 \pm \sqrt{1024+126672}}{104} \quad \color {Red} \text {Exponent, then multiplication.}\\ t &= \dfrac{32 \pm \sqrt{127696}}{104} \quad \color {Red} \text { Simplify. } \end{align*} \nonumber \]
Ahora, como la solicitud es por un tiempo aproximado, no nos molestaremos con la forma simple y la reducción, sino que procederemos inmediatamente a la calculadora para aproximar este último resultado (ver Figura\(\PageIndex{4}\)). Así, Arnie lleva aproximadamente\(3.743709336\) horas montando. Para cambiar la parte fraccionaria\(0.743709336\) horas a minutos, multiplique por\(60\) min/hr.

Figura\(\PageIndex{4}\): Tiempo aproximado que Arnie ha estado montando.

\[0.743709336 \mathrm{hr}=0.743709336 \mathrm{hr} \times \dfrac{60 \mathrm{min}}{\mathrm{hr}}=44.62256016 \mathrm{min} \nonumber \]

Redondeando al minuto más cercano, Arnie ha estado montando aproximadamente\(3\) horas y\(45\) minutos. Debido a que Arnie comenzó a montar a mediodía, la hora a la que él y Barbara están\(50\) a kilómetros de distancia es aproximadamente a las 3:45 PM.

Ejercicio\(\PageIndex{5}\)

A las 6:00 AM, un tren de carga pasa por Sagebrush Junction en dirección oeste a\(40\) millas por hora. A las 8:00 AM, un tren de pasajeros pasa por el cruce en dirección sur a\(60\) millas por hora. ¿A qué hora del día, correcta al minuto más cercano, estarán los dos trenes\(180\) a millas de distancia?

Responder

9:42AM