Capítulo 1 Ejercicios de revisión
- Page ID
- 110425
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ejercicios de revisión de capítulos
Introducción a los números enteros
Usar valor posicional con número entero
En los siguientes ejercicios encontrarás el valor posicional de cada dígito.
26,915
- 1
- 2
- 9
- 5
- 6
- Contestar
-
- decenas
- diez miles
- cientos
- unos
- miles
359,417
- 9
- 3
- 4
- 7
- 1
58,129,304
- 5
- 0
- 1
- 8
- 2
- Contestar
-
- diez millones
- decenas
- cien miles
- millones
- diez miles
9,430,286,157
- 6
- 4
- 9
- 0
- 5
En los siguientes ejercicios, nombra cada número.
6,104
- Contestar
-
seis mil ciento cuatro
493,068
3,975,284
- Contestar
-
tres millones novecientos setenta y cinco mil doscientos ochenta y cuatro
85,620,435
En los siguientes ejercicios, escribe cada número como un número entero usando dígitos.
trescientos quince
- Contestar
-
315
sesenta y cinco mil novecientos doce
noventa millones cuatrocientos veinticinco mil dieciséis
- Contestar
-
90,425,016
mil millones, cuarenta y tres millones, novecientos veintidós mil trescientos once
En los siguientes ejercicios, redondear al valor posicional indicado.
Redondea al diez más cercano.
- 407
- 8,564
- Contestar
-
- 410
- 8,560
Redondear al cien más cercano.
- 25,846
- 25,864
En los siguientes ejercicios, redondear cada número al más cercano 1. cien 2. mil 3. diez mil.
864,951
- Contestar
-
- 865,000865.000
- 865,000865.000
- 860,000
3,972,849
Identificar múltiplos y factores
En los siguientes ejercicios, utilice las pruebas de divisibilidad para determinar si cada número es divisible por 2, por 3, por 5, por 6 y por 10.
168
- Contestar
-
por 2,3,6
264
375
- Contestar
-
por 3,5
750
1430
- Contestar
-
por 2,5,10
1080
Encuentre factorizaciones principales y múltiplos menos comunes
En los siguientes ejercicios, encuentra la factorización principal.
420
- Contestar
-
2\(\cdot 2 \cdot 3 \cdot 5 \cdot 7\)
115
225
- Contestar
-
3\(\cdot 3 \cdot 5 \cdot 5\)
2475
1560
- Contestar
-
\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 5 \cdot 13\)
56
72
- Contestar
-
\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 3\)
168
252
- Responder
-
\(2 \cdot 2 \cdot 3 \cdot 3 \cdot 7\)
391
En los siguientes ejercicios, encuentra el múltiplo menos común de los siguientes números usando el método múltiplos.
6,15
- Responder
-
30
60, 75
En los siguientes ejercicios, encuentra el múltiplo menos común de los siguientes números usando el método de factores primos.
24, 30
- Responder
-
120
70, 84
Usar el lenguaje del álgebra
Usar variables y símbolos algebraicos
En los siguientes ejercicios, traduzca lo siguiente del álgebra al inglés.
25−7
- Responder
-
25 menos 7, la diferencia de veinticinco y siete
5\(\cdot 6\)
\(45 \div 5\)
- Responder
-
45 dividido por 5, el cociente de cuarenta y cinco y cinco
x+8
\(42 \geq 27\)
- Responder
-
cuarenta y dos es mayor o igual a veintisiete
3n=24
\(3 \leq 20 \div 4\)
- Responder
-
3 es menor o igual a 20 dividido por 4, tres es menor o igual al cociente de veinte y cuatro
\(a \neq 7 \cdot 4\)
En los siguientes ejercicios, determine si cada uno es una expresión o una ecuación.
\(6 \cdot 3+5\)
- Responder
-
expresión
y−8=32
Simplificar las expresiones usando el orden de las operaciones
En los siguientes ejercicios, simplifique cada expresión.
\(3^{5}\)
- Responder
-
243
\(10^{8}\)
En los siguientes ejercicios, simplifique
6+10/2+2
- Responder
-
13
9+12/3+4
\(20 \div(4+6) \cdot 5\)
- Responder
-
10
\(33 \div(3+8) \cdot 2\)
\(4^{2}+5^{2}\)
- Responder
-
41
\((4+5)^{2}\)
Evaluar una expresión
En los siguientes ejercicios, evalúe las siguientes expresiones.
9x+7 cuando x=3
- Responder
-
34
5x−4 cuando x=6
\(x^{4}\)cuando\(x=3\)
- Responder
-
81
\(3^{x}\)cuando\(x=3\)
\(x^{2}+5 x-8\)cuando\(x=6\)
- Responder
-
58
\(2 x+4 y-5\)cuando
\(x=7, y=8\)
Simplificar expresiones combinando términos similares
En los siguientes ejercicios, identificar el coeficiente de cada término.
12n
- Responder
-
12
9\(x^{2}\)
En los siguientes ejercicios, identifique los términos similares.
\(3 n, n^{2}, 12,12 p^{2}, 3,3 n^{2}\)
- Responder
-
12 y\(3, n^{2}\) y 3\(n^{2}\)
\(5,18 r^{2}, 9 s, 9 r, 5 r^{2}, 5 s\)
En los siguientes ejercicios, identificar los términos en cada expresión.
\(11 x^{2}+3 x+6\)
- Responder
-
\(11 x^{2}, 3 x, 6\)
\(22 y^{3}+y+15\)
En los siguientes ejercicios, simplifique las siguientes expresiones combinando términos similares.
17a+9a
- Responder
-
26a
18z+9z
9x+3x+8
- Responder
-
12x+8
8a+5a+9
7p+6+5p−4
- Responder
-
12p+2
8x+7+4x−5
Traducir una frase en inglés a una expresión algebraica
En los siguientes ejercicios, traduzca las siguientes frases en expresiones algebraicas.
la suma de 8 y 12
- Responder
-
8+12
la suma de 9 y 1
la diferencia de x y 4
- Responder
-
x−4
la diferencia de x y 3
el producto de 6 y y
- Responder
-
6y
el producto de 9 y y
Adele compró una falda y una blusa. La falda costó 15 dólares más que la blusa. Deja que bb represente el costo de la blusa. Escribe una expresión por el costo de la falda.
- Responder
-
b+15
Marcella tiene 6 primos niños menos que primos niñas. Que g represente el número de primos niñas. Escribe una expresión para el número de primos chicos.
Sumar y restar números enteros
Usar negativos y opuestos de enteros
En los siguientes ejercicios, ordene cada uno de los siguientes pares de números, utilizando < or >.
- 6___2
- −7___4
- −9___−1
- 9___−3
- Responder
-
- >
- <
- <
- >
- −5___1
- −4___−9
- 6___10
- 3___−8
En los siguientes ejercicios,, encuentra lo contrario de cada número.
- −8
- 1
- Responder
-
- 8
- −1
- −2
- 6
En los siguientes ejercicios, simplifique.
− (−19)
- Responder
-
19
− (−53)
En los siguientes ejercicios, simplifique.
−m cuando
- m=3
- m=−3
- Responder
-
- −3
- 3
−p cuando
- p=6
- p=−6
Simplificar expresiones con valor absoluto
En los siguientes ejercicios,, simplificar.
- |7|
- |−25|
- |0|
- Responder
-
- 7
- 25
- 0
- |5|
- |0|
- |−19|
En los siguientes ejercicios, rellene <, > o = para cada uno de los siguientes pares de números.
- −8___|−8|
- −|−2|___−2
- Responder
-
- <
- =
- |−3|___−|−3|
- 4___−|−4|
En los siguientes ejercicios, simplifique.
|8−4|
- Responder
-
4
|9−6|
8 (14−2|−2|)
- Responder
-
80
6 (13−4|−2|)
En los siguientes ejercicios, evalúe.
1. |x| cuando x=−28
- Responder
-
- 28
- 15
- ycuando y=−37
- |−z| cuando z=−24
Agregar enteros
En los siguientes ejercicios, simplifique cada expresión.
−200+65
- Responder
-
−135
−150+45
2+ (−8) +6
- Responder
-
0
4+ (−9) +7
140+ (−75) +67
- Responder
-
132
−32+24+ (−6) +10
Restar enteros
En los siguientes ejercicios, simplifique.
9−3
- Responder
-
6
−5− (−1)
- 15−6
- 15+ (−6)
- Responder
-
- 9
- 9
- 12−9
- 12+ (−9)
- 8− (−9)
- 8+9
- Responder
-
- 17
- 17
- 4− (−4)
- 4+4
En los siguientes ejercicios, simplifique cada expresión.
10− (−19)
- Responder
-
29
11− (−18)
31−79
- Responder
-
−48
39−81
−31−11
- Responder
-
−42
−32−18
−15− (−28) +5
- Responder
-
18
71+ (−10) −8
−16− (−4+1) −7
- Responder
-
-20
−15− (−6+4) −3
Multiplicar enteros
En los siguientes ejercicios, multiplicar.
−5 (7)
- Responder
-
−35
−8 (6)
−18 (−2)
- Responder
-
36
−10 (−6)
Dividir enteros
En los siguientes ejercicios, divide.
\(-28 \div 7\)
- Responder
-
-4
\(56 \div(-7)\)
\(-120 \div(-20)\)
- Responder
-
6
\(-200 \div 25\)
Simplificar expresiones con números enteros
En los siguientes ejercicios, simplifique cada expresión.
−8 (−2) −3 (−9)
- Responder
-
43
−7 (−4) −5 (−3)
\((-5)^{3}\)
- Responder
-
−125
\((-4)^{3}\)
\(-4 \cdot 2 \cdot 11\)
- Responder
-
−88
\(-5 \cdot 3 \cdot 10\)
\(-10(-4) \div(-8)\)
- Responder
-
-5
\(-8(-6) \div(-4)\)
31−4 (3−9)
- Responder
-
55
24−3 (2−10)
Evaluar expresiones variables con números enteros
En los siguientes ejercicios, evalúe cada expresión.
x+8 cuando
- x=−26
- x=−95
- Responder
-
- −18
- −87
y+9 cuando
- y=−29
- y=−84
Cuando b=−11, evalúe:
- b+6
- −b+6
- Responder
-
- −5
- 17
Cuando c=−9, evalúe:
- c+ (−4) c+ (−4)
- −c+ (−4)
\(p^{2}-5 p+2\)cuando
\(p=-1\)
- Responder
-
8
\(q^{2}-2 q+9\)cuando\(q=-2\)
\(6 x-5 y+15\)cuándo\(x=3\) y\(y=-1\)
- Responder
-
38
\(3 p-2 q+9\)cuándo\(p=8\) y\(q=-2\)
Traducir frases en inglés a expresiones algebraicas
En los siguientes ejercicios, traduzca a una expresión algebraica y simplifique si es posible.
la suma de −4 y −17, incrementada en 32
- Responder
-
(−4+ (−17)) +32; 11
- la diferencia de 15 y −7
- restar 15 de −7
el cociente de −45 y −9
- Responder
-
\(\frac{-45}{-9} ; 5\)
el producto de −12 y la diferencia de c y d
Usar números enteros en aplicaciones
En los siguientes ejercicios, resuelve.
Temperatura La temperatura alta un día en Miami Beach, Florida, fue de 76°. Ese mismo día, la alta temperatura en Buffalo, Nueva York fue de −8°. ¿Cuál fue la diferencia entre la temperatura en Miami Beach y la temperatura en Buffalo?
- Responder
-
84 grados
Cuenta corriente Adrianne tiene un saldo de −$22 en su cuenta corriente. Ella deposita 301 dólares en la cuenta. ¿Cuál es el nuevo saldo?
Visualizar Fracciones
Buscar Fracciones Equivalentes
En los siguientes ejercicios, encuentra tres fracciones equivalentes a la fracción dada. Muestra tu obra, usando figuras o álgebra.
\(\frac{1}{4}\)
- Responder
-
\(\frac{2}{8}, \frac{3}{12}, \frac{4}{16}\)las respuestas pueden variar
\(\frac{1}{3}\)
\(\frac{5}{6}\)
- Responder
-
\(\frac{10}{12}, \frac{15}{18}, \frac{20}{24}\)las respuestas pueden variar
\(\frac{2}{7}\)
Simplificar fracciones
En los siguientes ejercicios, simplifique.
\(\frac{7}{21}\)
- Contestar
-
\(\frac{1}{3}\)
\(\frac{8}{24}\)
\(\frac{15}{20}\)
- Contestar
-
\(\frac{3}{4}\)
\(\frac{12}{18}\)
\(-\frac{168}{192}\)
- Contestar
-
\(-\frac{7}{8}\)
\(-\frac{140}{224}\)
\(\frac{11 x}{11 y}\)
- Contestar
-
\(\frac{x}{y}\)
\(\frac{15 a}{15 b}\)
Multiplicar fracciones
En los siguientes ejercicios, multiplicar.
\(\frac{2}{5} \cdot \frac{1}{3}\)
- Contestar
-
\(\frac{2}{15}\)
\(\frac{1}{2} \cdot \frac{3}{8}\)
\(\frac{7}{12}\left(-\frac{8}{21}\right)\)
- Contestar
-
\(-\frac{2}{9}\)
\(\frac{5}{12}\left(-\frac{8}{15}\right)\)
\(-28 p\left(-\frac{1}{4}\right)\)
- Contestar
-
7p
\(-51 q\left(-\frac{1}{3}\right)\)
\(\frac{14}{5}(-15)\)
- Contestar
-
−42
\(-1\left(-\frac{3}{8}\right)\)
Dividir fracciones
En los siguientes ejercicios, divide
\(\frac{1}{2} \div \frac{1}{4}\)
- Contestar
-
2
\(\frac{1}{2} \div \frac{1}{8}\)
\(-\frac{4}{5} \div \frac{4}{7}\)
- Contestar
-
\(-\frac{7}{5}\)
\(-\frac{3}{4} \div \frac{3}{5}\)
\(\frac{5}{8} \div \frac{a}{10}\)
- Contestar
-
\(\frac{25}{4 a}\)
\(\frac{5}{6} \div \frac{c}{15}\)
\(\frac{7 p}{12} \div \frac{21 p}{8}\)
- Contestar
-
\(\frac{2}{9}\)
\(\frac{5 q}{12} \div \frac{15 q}{8}\)
\(\frac{2}{5} \div(-10)\)
- Contestar
-
\(-\frac{1}{25}\)
\(-18 \div-\left(\frac{9}{2}\right)\)
En los siguientes ejercicios, simplifique.
\(\frac{\frac{2}{3}}{\frac{8}{9}}\)
- Contestar
-
\(\frac{3}{4}\)
\(\frac{\frac{4}{5}}{\frac{8}{15}}\)
\(\frac{-\frac{9}{10}}{3}\)
- Contestar
-
\(-\frac{3}{10}\)
\(\frac{2}{\frac{5}{8}}\)
\(\frac{\frac{r}{5}}{\frac{s}{3}}\)
- Contestar
-
\(\frac{3 r}{5 s}\)
\(\frac{-\frac{x}{6}}{-\frac{8}{9}}\)
Simplificar expresiones escritas con una barra de fracciones
En los siguientes ejercicios, simplifique.
\(\frac{4+11}{8}\)
- Contestar
-
\(\frac{15}{8}\)
\(\frac{9+3}{7}\)
\(\frac{30}{7-12}\)
- Contestar
-
-6
\(\frac{15}{4-9}\)
\(\frac{22-14}{19-13}\)
- Contestar
-
\(\frac{4}{3}\)
\(\frac{15+9}{18+12}\)
\(\frac{5 \cdot 8}{-10}\)
- Contestar
-
-4
\(\frac{3 \cdot 4}{-24}\)
\(\frac{15 \cdot 5-5^{2}}{2 \cdot 10}\)
- Contestar
-
\(\frac{5}{2}\)
\(\frac{12 \cdot 9-3^{2}}{3 \cdot 18}\)
\(\frac{2+4(3)}{-3-2^{2}}\)
- Contestar
-
-2
\(\frac{7+3(5)}{-2-3^{2}}\)
Traducir frases a expresiones con fracciones
En los siguientes ejercicios, traduzca cada frase en inglés a una expresión algebraica.
el cociente de c y la suma de d y 9.
- Contestar
-
\(\frac{c}{d+9}\)
el cociente de la diferencia de h y k, y −5.
Sumar y restar fracciones
Suma y resta fracciones con un denominador común
En los siguientes ejercicios, agregue.
\(\frac{4}{9}+\frac{1}{9}\)
- Contestar
-
\(\frac{5}{9}\)
\(\frac{2}{9}+\frac{5}{9}\)
\(\frac{y}{3}+\frac{2}{3}\)
- Contestar
-
\(\frac{y+2}{3}\)
\(\frac{7}{p}+\frac{9}{p}\)
\(-\frac{1}{8}+\left(-\frac{3}{8}\right)\)
- Contestar
-
\(-\frac{1}{2}\)
\(-\frac{1}{8}+\left(-\frac{5}{8}\right)\)
En los siguientes ejercicios, restar.
\(\frac{4}{5}-\frac{1}{5}\)
- Contestar
-
\(\frac{3}{5}\)
\(\frac{4}{5}-\frac{3}{5}\)
\(\frac{y}{17}-\frac{9}{17}\)
- Contestar
-
\(\frac{y-9}{17}\)
\(\frac{x}{19}-\frac{8}{19}\)
\(-\frac{8}{d}-\frac{3}{d}\)
- Contestar
-
\(-\frac{11}{d}\)
\(-\frac{7}{c}-\frac{7}{c}\)
Suma o resta fracciones con diferentes denominadores
En los siguientes ejercicios, sumar o restar.
\(\frac{1}{3}+\frac{1}{5}\)
- Contestar
-
\(\frac{8}{15}\)
\(\frac{1}{4}+\frac{1}{5}\)
\(\frac{1}{5}-\left(-\frac{1}{10}\right)\)
- Contestar
-
\(\frac{3}{10}\)
\(\frac{1}{2}-\left(-\frac{1}{6}\right)\)
\(\frac{2}{3}+\frac{3}{4}\)
- Contestar
-
\(\frac{17}{12}\)
\(\frac{3}{4}+\frac{2}{5}\)
\(\frac{11}{12}-\frac{3}{8}\)
- Contestar
-
\(\frac{13}{24}\)
\(\frac{5}{8}-\frac{7}{12}\)
\(-\frac{9}{16}-\left(-\frac{4}{5}\right)\)
- Contestar
-
\(\frac{19}{80}\)
\(-\frac{7}{20}-\left(-\frac{5}{8}\right)\)
\(1+\frac{5}{6}\)
- Contestar
-
\(\frac{11}{6}\)
\(1-\frac{5}{9}\)
Utilice el orden de operaciones para simplificar fracciones complejas
En los siguientes ejercicios, simplifique.
\(\frac{\left(\frac{1}{5}\right)^{2}}{2+3^{2}}\)
- Contestar
-
\(\frac{1}{275}\)
\(\frac{\left(\frac{1}{3}\right)^{2}}{5+2^{2}}\)
\(\frac{\frac{2}{3}+\frac{1}{2}}{\frac{3}{4}-\frac{2}{3}}\)
- Contestar
-
14
\(\frac{\frac{3}{4}+\frac{1}{2}}{\frac{5}{6}-\frac{2}{3}}\)
Evaluar expresiones variables con fracciones
En los siguientes ejercicios, evalúe.
\(x+\frac{1}{2}\)cuando
- \(x=-\frac{1}{8}\)
- \(x=-\frac{1}{2}\)
- Contestar
-
- \(\frac{3}{8}\)
- \(0\)
\(x+\frac{2}{3}\)cuando
- \(x=-\frac{1}{6}\)
- \(x=-\frac{5}{3}\)
4\(p^{2} q\) cuando\(p=-\frac{1}{2}\) y\(q=\frac{5}{9}\)
- Contestar
-
\(\frac{5}{9}\)
5\(m^{2} n\) cuando\(m=-\frac{2}{5}\) y\(n=\frac{1}{3}\)
\(\frac{u+v}{w}\)cuando
\(u=-4, v=-8, w=2\)
- Contestar
-
-6
\(\frac{m+n}{p}\)cuando
\(m=-6, n=-2, p=4\)
Decimales
Nombrar y escribir decimales
En los siguientes ejercicios, escribe como decimal.
Ocho y tres centésimas
- Contestar
-
8.03
Nueve y siete centésimas
Una milésima
- Contestar
-
0.001
Nueve milésimas
En los siguientes ejercicios, nombra cada decimal.
7.8
- Contestar
-
siete y ocho décimas
5.01
0.005
- Contestar
-
cinco milésimas
0.381
Decimales Redondos
En los siguientes ejercicios, redondea cada número al
- centésima
- décimo
- número entero.
5.7932
- Contestar
-
- 5.79
- 5.8
- 6
3.6284
12.4768
- Contestar
-
- 12.48
- 12.5
- 12
25.8449
Sumar y restar decimales
En los siguientes ejercicios, sumar o restar.
18.37+9.36
- Contestar
-
27.73
256.37−85.49
15.35−20.88
- Contestar
-
−5.53
37.5+12.23
−4.2+ (−9.3)
- Contestar
-
−13.5
−8.6+ (−8.6)
100−64.2
- Contestar
-
35.8
100−65.83
2.51+40
- Contestar
-
42.51
9.38+60
Multiplicar y dividir decimales
En los siguientes ejercicios, multiplicar.
(0.3) (0.4)
- Contestar
-
0.12
(0.6) (0.7)
(8.52) (3.14)
- Contestar
-
26.7528
(5.32) (4.86)
(0.09) (24.78)
- Contestar
-
2.2302
(0.04) (36.89)
En los siguientes ejercicios, divide.
\(0.15 \div 5\)
- Contestar
-
0.03
\(0.27 \div 3\)
\(\$ 8.49 \div 12\)
- Contestar
-
$0.71
\(\$ 16.99 \div 9\)
\(12 \div 0.08\)
- Contestar
-
150
\(5 \div 0.04\)
Convertir decimales, fracciones y porcentajes
En los siguientes ejercicios, escribe cada decimal como fracción.
0.08
- Contestar
-
\(\frac{2}{25}\)
0.17
0.425
- Contestar
-
\(\frac{17}{40}\)
0.184
1.75
- Contestar
-
\(\frac{7}{4}\)
0.035
En los siguientes ejercicios, convierte cada fracción a un decimal.
\(\frac{2}{5}\)
- Contestar
-
0.4
\(\frac{4}{5}\)
\(-\frac{3}{8}\)
- Contestar
-
−0.375
\(-\frac{5}{8}\)
\(\frac{5}{9}\)
- Contestar
-
\(0 . \overline{5}\)
\(\frac{2}{9}\)
\(\frac{1}{2}+6.5\)
- Contestar
-
7
\(\frac{1}{4}+10.75\)
En los siguientes ejercicios, convertir cada porcentaje a un decimal.
5%
- Contestar
-
0.05
9%
40%
- Contestar
-
0.4
50%
115%
- Contestar
-
1.15
125%
En los siguientes ejercicios, convertir cada decimal a un porcentaje.
0.18
- Contestar
-
18%
0.15
0.009
- Contestar
-
0.9%
0.008
1.5
- Contestar
-
150%
2.2
Los números reales
Simplifique las expresiones con raíces cuadradas
En los siguientes ejercicios, simplifique.
\(\sqrt{64}\)
- Contestar
-
8
\(\sqrt{144}\)
\(-\sqrt{25}\)
- Contestar
-
-5
\(-\sqrt{81}\)
Identificar números enteros, números racionales, números irracionales y números reales
En los siguientes ejercicios, escribe como la relación de dos enteros.
- 9
- 8.47
- Contestar
-
- \(\frac{9}{1}\)
- \(\frac{847}{100}\)
- −15
- 3.591
En los siguientes ejercicios, enumere el
- números racionales,
- números irracionales.
\(0.84,0.79132 \ldots, 1 . \overline{3}\)
- Contestar
-
- \(0.84,1.3\)
- \(0.79132 \ldots\)
\(2.3 \overline{8}, 0.572,4.93814 \ldots\)
En los siguientes ejercicios, identificar si cada número es racional o irracional.
- \(\sqrt{121}\)
- \(\sqrt{48}\)
- Contestar
-
- racional
- irracional
- \(\sqrt{56}\)
- \(\sqrt{16}\)
En los siguientes ejercicios, identifica si cada número es un número real o no un número real.
- \(\sqrt{-9}\)
- \(-\sqrt{169}\)
- Contestar
-
- no es un número real
- número real
- \(\sqrt{-64}\)
- \(-\sqrt{81}\)
En los siguientes ejercicios, enumere el
- números enteros,
- enteros,
- números racionales,
- números irracionales,
- números reales para cada conjunto de números.
\(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
- Contestar
-
- \(0, \sqrt{16}\)
- \(-4,0, \sqrt{16}\)
- \(-4,0, \frac{5}{6}, \sqrt{16}\)
- \(\sqrt{18}, 5.2537 \ldots\)
- \(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
\(-\sqrt{4}, 0 . \overline{36}, \frac{13}{3}, 6.9152 \ldots, \sqrt{48}, 10 \frac{1}{2}\)
Localizar fracciones en la línea numérica
En los siguientes ejercicios, ubique los números en una recta numérica.
\(\frac{2}{3}, \frac{5}{4}, \frac{12}{5}\)
- Contestar
-
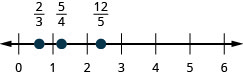
\(\frac{1}{3}, \frac{7}{4}, \frac{13}{5}\)
\(2 \frac{1}{3},-2 \frac{1}{3}\)
- Contestar
-
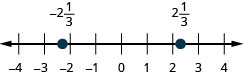
\(1 \frac{3}{5},-1 \frac{3}{5}\)
En los siguientes ejercicios, ordene cada uno de los siguientes pares de números, utilizando < or >.
−1___\(-\frac{1}{8}\)
- Contestar
-
<
\(-3 \frac{1}{4}\)___−4
\(-\frac{7}{9}\)___\(\frac{4}{9}\)
- Contestar
-
>
\(-2\)___\(\frac{19}{8}\)
Localizar decimales en la línea numérica
En los siguientes ejercicios, ubique en la recta numérica.
0.3
- Contestar
-
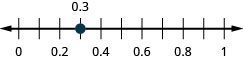
−0.2
−2.5
- Contestar
-
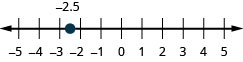
2.7
En los siguientes ejercicios, ordene cada uno de los siguientes pares de números, utilizando < or >.
0.9___0.6
- Contestar
-
>
0.7___0.8
−0.6___−0.59
- Contestar
-
>
−0.27___−0.3
Propiedades de Números Reales
Utilizar las propiedades conmutativas y asociativas
En los siguientes ejercicios, utilice la Propiedad Asociativa para simplificar.
−12 (4m)
- Contestar
-
−48m
30\(\left(\frac{5}{6} q\right)\)
(a+16) +31
- Contestar
-
a+47
(c+0.2) +0.7
En los siguientes ejercicios, simplifique.
6y+37+ (−6y)
- Contestar
-
37
\(\frac{1}{4}+\frac{11}{15}+\left(-\frac{1}{4}\right)\)
\(\frac{14}{11} \cdot \frac{35}{9} \cdot \frac{14}{11}\)
- Contestar
-
\(\frac{35}{9}\)
\(-18 \cdot 15 \cdot \frac{2}{9}\)
\(\left(\frac{7}{12}+\frac{4}{5}\right)+\frac{1}{5}\)
- Contestar
-
1\(\frac{7}{12}\)
(3.98d+0.75d) +1.25d
11x+8y+16x+15y
- Contestar
-
27x+23y
52m+ (−20n) + (−18m) + (−5n)
Utilizar la identidad y las propiedades inversas de la suma y la multiplicación
En los siguientes ejercicios, encuentra la inversa aditiva de cada número.
- \(\frac{1}{3}\)
- 5.1
- \(-14\)
- \(-\frac{8}{5}\)
- Contestar
-
- \(-\frac{1}{3}\)
- \(-5.1\)
- -14
- \(-\frac{8}{5}\)
- \(-\frac{7}{8}\)
- \(-0.03\)
- 17
- \(\frac{12}{5}\)
En los siguientes ejercicios, encuentra la inversa multiplicativa de cada número.
- \(10\)
- \(-\frac{4}{9}\)
- 0.6
- Contestar
-
- \(\frac{1}{10}\)
- \(-\frac{9}{4}\)
- \(\frac{5}{3}\)
- \(-\frac{9}{2}\)
- -7
- 2.1
Usa las Propiedades de Zero
En los siguientes ejercicios, simplifique.
83\(\cdot 0\)
- Contestar
-
0
\(\frac{0}{9}\)
\(\frac{5}{0}\)
- Contestar
-
undefined
\(0 \div \frac{2}{3}\)
En los siguientes ejercicios, simplifique.
43+39+ (−43)
- Contestar
-
39
(n+6.75) +0.25
\(\frac{5}{13} \cdot 57 \cdot \frac{13}{5}\)
- Contestar
-
57
\(\frac{1}{6} \cdot 17 \cdot 12\)
\(\frac{2}{3} \cdot 28 \cdot \frac{3}{7}\)
- Contestar
-
8
\(9(6 x-11)+15\)
Simplificar expresiones mediante la propiedad distributiva
En los siguientes ejercicios, simplifique el uso de la Propiedad Distributiva.
7 (x+9)
- Contestar
-
7x+63
9 (u−4)
−3 (6m−1)
- Contestar
-
−18m+3
−8 (−7a−12)
\(\frac{1}{3}(15 n-6)\)
- Contestar
-
5n−2
\((y+10) \cdot p\)
(a−4) − (6a+9)
- Contestar
-
−5a−13
4 (x+3) −8 (x−7)
Sistemas de Medición
1.1 Definir unidades de medida estadounidenses y convertir de una unidad a otra
En los siguientes ejercicios, convierte las unidades. Redondear a la décima más cercana.
Un árbol floral mide 7 pies de altura. Convierte la altura a pulgadas.
- Contestar
-
84 pulgadas
Un marco para fotos mide 42 pulgadas de ancho. Convierte el ancho a pies.
Kelly mide 5 pies y 4 pulgadas de alto. Convierte su altura a pulgadas.
- Contestar
-
64 pulgadas
Un área de juegos es de 45 pies de ancho. Convierta el ancho a yardas.
La altura del Monte Shasta es de 14,179 pies. Convierte la altura a millas.
- Contestar
-
2.7 millas
Shamu pesa 4.5 toneladas. Convierte el peso a libras.
La obra duró\(1\frac{3}{4}\) horas. Convertir el tiempo a minutos.
- Contestar
-
105 minutos
¿Cuántas cucharadas hay en un cuarto de galón?
El bebé de Naomi pesaba 5 libras 14 onzas al nacer. Convierte el peso a onzas.
- Contestar
-
94 onzas
Trinh necesita 30 tazas de pintura para su proyecto de arte de clase. Convertir el volumen a galones.
Utilice Unidades Mixtas de Medida en el Sistema de Estados Unidos.
En los siguientes ejercicios, resuelve.
John atrapó 4 langostas. Los pesos de las langostas fueron 1 libra 9 onzas, 1 libra 12 onzas, 4 libras 2 onzas y 2 libras 15 onzas. ¿Cuál fue el peso total de las langostas?
- Contestar
-
10 lbs. 6 oz.
Todos los días de la semana pasada Pedro registraba la cantidad de minutos que pasaba leyendo. El número de minutos fue de 50, 25, 83, 45, 32, 60, 135. ¿Cuántas horas pasó Pedro leyendo?
Fouad mide 6 pies y 2 pulgadas de alto. Si se para en un peldaño de una escalera de 8 pies y 10 pulgadas de alto, ¿qué tan alto del suelo está la parte superior de la cabeza de Fouad?
- Contestar
-
15 pies
Dalila quiere hacer fundas de almohada. Cada funda toma 30 pulgadas de tela. ¿Cuántos metros de tela necesita para 4 fundas?
Hacer conversiones de unidades en el sistema métrico
En los siguientes ejercicios, convierte las unidades.
Donna mide 1.7 metros de altura. Convierte su estatura a centímetros.
- Contestar
-
170 centímetros
El Monte Everest mide 8,850 metros de altura. Convertir la altura a kilómetros.
Una taza de yogur contiene 488 miligramos de calcio. Convierte esto a gramos.
- Contestar
-
0.488 gramos
Una taza de yogur contiene 13 gramos de proteína. Convierte esto a miligramos.
Sergio pesaba 2.9 kilogramos al nacer. Convierte esto a gramos.
- Contestar
-
2,900 gramos
Una botella de agua contenía 650 mililitros. Convierte esto a litros.
Utilizar Unidades Mixtas de Medida en el Sistema Métrico
En los siguientes esfuerzos, resuelva.
Minh mide 2 metros de altura. Su hija mide 88 centímetros de altura. ¿Cuánto más alto es Minh que su hija?
- Contestar
-
1.12 metros
Selma tenía una botella de agua de 1 litro. Si bebió 145 mililitros, ¿cuánta agua quedaba en la botella?
Una porción de jugo de arándano contiene 30 gramos de azúcar. ¿Cuántos kilogramos de azúcar hay en 30 porciones de jugo de arándano?
- Contestar
-
0.9 kilogramos
Una onza de tofu proporcionó 2 gramos de proteína. ¿Cuántos miligramos de proteína son proporcionados por 5 onzas de tofu?
Convertir entre EE. UU. y los sistemas métricos de medición
En los siguientes ejercicios, realice las conversiones unitarias. Redondear a la décima más cercana.
Majid mide 69 pulgadas de alto. Convertir su estatura a centímetros.
- Contestar
-
175.3 centímetros
Una cancha de basquetbol universitario mide 84 pies de largo. Convierte esta longitud en metros.
Caroline caminó 2.5 kilómetros. Convierta esta longitud en millas.
- Contestar
-
1.6 millas
Lucas pesa 78 kilogramos. Convierte su peso en libras.
El auto de Steve tiene capacidad para 55 litros de gasolina. Convierte esto en galones.
- Contestar
-
14.6 galones
Una caja de libros pesa 25 libras. Convertir el peso a kilogramos.
Convertir entre temperaturas Fahrenheit y Celsius
En los siguientes ejercicios, convertir las temperaturas de Fahrenheit a grados Celsius. Redondear a la décima más cercana.
95° Fahrenheit
- Contestar
-
35° C
23° Fahrenheit
20° Fahrenheit
- Contestar
-
—6.7° C
64° Fahrenheit
En los siguientes ejercicios, convertir las temperaturas Celsius a grados Fahrenheit. Redondear a la décima más cercana.
30° Celsius
- Contestar
-
86° F
—5° Celsius
—12° Celsius
- Contestar
-
10.4° F
24° Celsius
Prueba de práctica de capítulo
Escribe como un número entero usando dígitos: doscientos cinco mil, seiscientos diecisiete.
- Contestar
-
205,617
Encuentra la factorización prima de 504.
Encuentra el múltiplo menos común de 18 y 24.
- Contestar
-
72
Combina términos similares: 5n+8+2n−1.
En los siguientes ejercicios, evalúe.
\(-|x|\)cuando\(x=-2\)
- Contestar
-
−2
11−a cuando a=−3
Traducir a una expresión algebraica y simplificar: veinte menos que negativo 7.
- Contestar
-
−7−20; −27
Monique tiene un saldo de −$18 en su cuenta corriente. Ella deposita 152 dólares en la cuenta. ¿Cuál es el nuevo saldo?
Vuelta 677.1348 a la centésima más cercana.
- Contestar
-
677.13
Convertir\(\frac{4}{5}\) a decimal.
Convertir 1.85 a un por ciento.
- Contestar
-
185%
Localizar\(\frac{2}{3},-1.5,\) y\(\frac{9}{4}\) en una línea numérica.
En los siguientes ejercicios, simplifique cada expresión.
\(4+10(3+9)-5^{2}\)
- Contestar
-
99
−85+42
−19−25
- Responder
-
−44
\((-2)^{4}\)
\(-5(-9) \div 15\)
- Responder
-
3
\(\frac{3}{8} \cdot \frac{11}{12}\)
\(\frac{4}{5} \div \frac{9}{20}\)
- Responder
-
\(\frac{16}{9}\)
\(\frac{12+3 \cdot 5}{15-6}\)
\(\frac{m}{7}+\frac{10}{7}\)
- Responder
-
\(\frac{m+10}{7}\)
\(\frac{7}{12}-\frac{3}{8}\)
\(-5.8+(-4.7)\)
- Responder
-
−10.5
100−64.25
(0.07) (31.95)
- Responder
-
2.2365
\(9 \div 0.05\)
\(-14\left(\frac{5}{7} p\right)\)
- Responder
-
−10p
(u+8) −9
6x+ (−4y) +9x+8y
- Responder
-
15x+4 años
\(\frac{0}{23}\)
\(\frac{75}{0}\)
- Responder
-
undefined
−2 (13q−5)
Una película duró 1\(\frac{2}{3}\) horas. ¿Cuántos minutos duró? (1 hora\(=60\) minutos)
- Responder
-
100 minutos
Mike's SUV mide 5 pies y 11 pulgadas de alto. Quiere poner una bolsa de carga en la azotea en la camioneta. La bolsa de carga mide 1 pie y 6 pulgadas de alto. ¿Cuál será la altura total del SUV con la bolsa de carga en el techo? (1 pie = 12 pulgadas)
Jennifer corrió 2.8 millas. Convierte esta longitud en kilómetros. (1 milla = 1.61 kilómetros)
- Responder
-
4.508 km


