10.3: Resolver ecuaciones cuadráticas usando la fórmula cuadrática
- Page ID
- 110194
Al final de esta sección, podrás:
- Resolver ecuaciones cuadráticas usando la fórmula cuadrática
- Utilizar el discriminante para predecir el número de soluciones de una ecuación cuadrática
- Identificar el método más apropiado para resolver una ecuación cuadrática
Cuando resolvimos ecuaciones cuadráticas en la última sección completando el cuadrado, dimos los mismos pasos cada vez. Al final del conjunto de ejercicios, quizás te hayas estado preguntando '¿no hay una manera más fácil de hacer esto?' La respuesta es 'sí'. En esta sección, derivaremos y usaremos una fórmula para encontrar la solución de una ecuación cuadrática.
Ya hemos visto cómo resolver una fórmula para una variable específica 'en general' para que hagamos los pasos algebraicos solo una vez y luego usaríamos la nueva fórmula para encontrar el valor de la variable específica. Ahora, pasaremos por los pasos de completar el cuadrado en general para resolver una ecuación cuadrática para x. Puede ser útil mirar uno de los ejemplos al final de la última sección donde resolvimos una ecuación de la forma a\( ax^2+bx+c=0\) medida que lee los pasos algebraicos a continuación, para que los vea con números así como 'en general'.
| Comenzamos con la forma estándar de una ecuación cuadrática y la resolvemos para x completando el cuadrado. | \( ax^2+bx+c=0\) | |
| Aísle los términos variables en un lado. | \( ax^2+bx=−c\) | |
| Hacer coeficiente principal 1, dividiendo por a. | \(\frac{ax^2}{a}+\frac{b}{a}x=−\frac{c}{a}\) | |
| Simplificar. | \(x^2+\frac{b}{a}x=−\frac{c}{a}\) | |
|
Para completar el cuadrado, búsquelo\((\frac{1}{2}·\frac{b}{a})^2\) y agrégalo a ambos lados de la ecuación. \((\frac{1}{2}\frac{b}{a})^2=\frac{b^2}{4a^2}\) |
\(x^2+\frac{b}{a}x+\frac{b^2}{4a^2}=−\frac{c}{a}+\frac{b^2}{4a^2}\) | |
| El lado izquierdo es un cuadrado perfecto, factorial. | \((x+\frac{b}{2a})^2=−\frac{c}{a}+\frac{b^2}{4a^2}\) | |
| Encuentra el denominador común del lado derecho y escribe fracciones equivalentes con el denominador común. | \((x+\frac{b}{2a})^2=−\frac{c·4a}{a·4a}+\frac{b^2}{4a^2}\) | |
| Simplificar. | \((x+\frac{b}{2a})^2=\frac{b^2}{4a^2}−\frac{4ac}{4a^2}\) | |
| Combine a una fracción. | \((x+\frac{b}{2a})^2=\frac{b^2−4ac}{4a^2}\) | |
| Utilice la propiedad raíz cuadrada. | \((x+\frac{b}{2a})=\pm\sqrt{\frac{b^2−4ac}{4a^2}}\) | |
| Simplificar. | \((x+\frac{b}{2a})=\pm\frac{\sqrt{b^2−4ac}}{2a}\) | |
| Agregar\(−\frac{b}{2a} \) a ambos lados de la ecuación. | \(x=−\frac{b}{2a}\pm\frac{\sqrt{b^2−4ac}}{2a}\) | |
| Combina los términos en el lado derecho. | \(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\) | |
Esta última ecuación es la Fórmula Cuadrática.
Las soluciones a una ecuación cuadrática de la forma\(ax^2+bx+c=0\),\(a\ge 0\) vienen dadas por la fórmula:
\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\)
Para usar la Fórmula Cuadrática, sustituimos los valores de a, b y c en la expresión del lado derecho de la fórmula. Entonces, hacemos todas las matemáticas para simplificar la expresión. El resultado da la (s) solución (es) a la ecuación cuadrática.
Cómo Resolver una Ecuación Cuadrática Usando la Fórmula Cuadrática
Resuelve\(2x^2+9x−5=0\) usando la Fórmula Cuadrática.
- Contestar
-


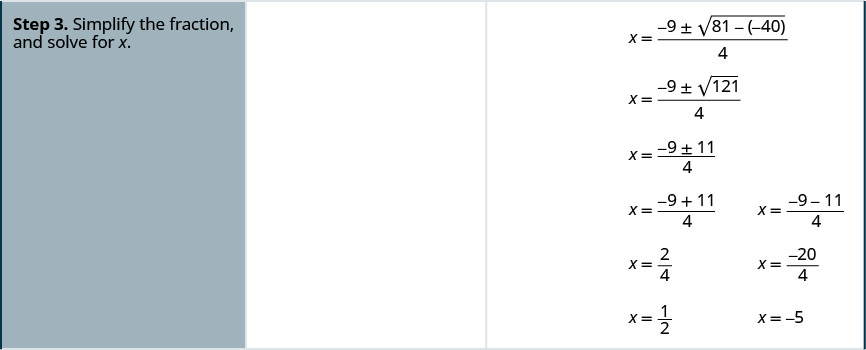

Resuelve\(3y^2−5y+2=0\) usando la Fórmula Cuadrática.
- Contestar
-
\(y=\frac{2}{3}\),\(y=1\)
Resuelve\(4z^2+2z−6=0\) usando la Fórmula Cuadrática.
- Contestar
-
\(z=−\frac{3}{2}\),\(z=1\)
- Escribe la Fórmula Cuadrática en forma estándar. Identificar los valores aa, bb y cc.
- Escribe la Fórmula Cuadrática. Luego sustituya en los valores de a, b y c.
- Simplificar.
- Consulta las soluciones.
Si dices la fórmula a medida que la escribes en cada problema, la tendrás memorizada en poco tiempo. Y recuerden, la Fórmula Cuadrática es una ecuación. Asegúrate de comenzar con '\(x=\)'.
Resuelve\(x^2−6x+5=0\) usando la Fórmula Cuadrática.
- Contestar
-

Esta ecuación está en forma estándar. 
Identificar los valores a, b, c. 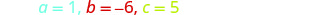
Escribe la Fórmula Cuadrática. 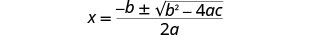
Después sustituya en los valores de a, b, c. 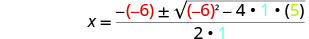
Simplificar. 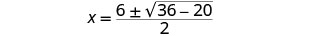
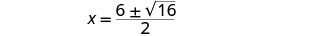
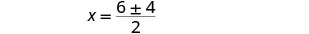
Reescribe para mostrar dos soluciones. 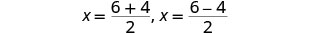
Simplificar. 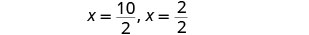
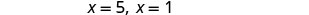
Cheque.
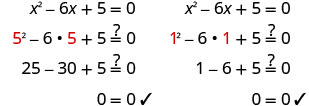
Resuelve\(a^2−2a−15=0\) usando la Fórmula Cuadrática.
- Contestar
-
\(a=−3\),\(a=5\)
Resuelve\(b^2+10b+24=0\) usando la Fórmula Cuadrática.
- Contestar
-
\(b=−6\),\(b=−4\)
Cuando resolvimos ecuaciones cuadráticas usando la Propiedad Raíz Cuadrada, a veces obtuvimos respuestas que tenían radicales. Eso puede suceder, también, al usar la Fórmula Cuadrática. Si obtenemos un radical como solución, la respuesta final debe tener el radical en su forma simplificada.
Resuelve\(4y^2−5y−3=0\) usando la Fórmula Cuadrática.
- Contestar
-
Podemos usar la Fórmula Cuadrática para resolver para la variable en una ecuación cuadrática, ya sea que se llame o no 'x'.

Esta ecuación está en forma estándar. 
Identificar los valores a, b, c. 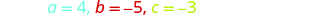
Escribe la Fórmula Cuadrática. 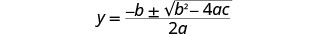
Después sustituya en los valores de a, b, c. 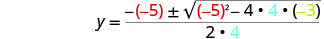
Simplificar. 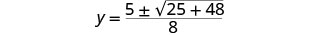
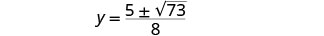
Reescribe para mostrar dos soluciones. 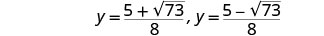
Cheque. Te dejamos el cheque a ti.
Resuelve\(2p^2+8p+5=0\) usando la Fórmula Cuadrática.
- Contestar
-
\(p=\frac{−4\pm\sqrt{6}}{2}\)
Resuelve\(5q^2−11q+3=0\) usando la Fórmula Cuadrática.
- Contestar
-
\(q=\frac{11\pm\sqrt{61}}{10}\)
Resuelve\(2x^2+10x+11=0\) usando la Fórmula Cuadrática.
- Contestar
-

Esta ecuación está en forma estándar. 
Identificar los valores a, b, c. 
Escribe la Fórmula Cuadrática. 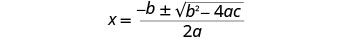
Después sustituya en los valores de a, b, c. 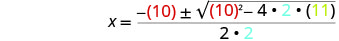
Simplificar. 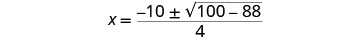
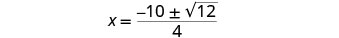
Simplifica lo radical. 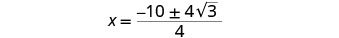
Facturar el factor común en el numerador. 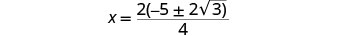
Eliminar los factores comunes. 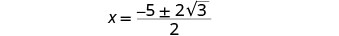
Reescribe para mostrar dos soluciones. 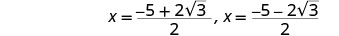
Cheque. Te dejamos el cheque a ti.
Resuelve\(3m^2+12m+7=0\) usando la Fórmula Cuadrática.
- Contestar
-
\(m=\frac{−6\pm\sqrt{15}}{3}\)
Resuelve\(5n^2+4n−4=0\) usando la Fórmula Cuadrática.
- Contestar
-
\(n=\frac{−2\pm2\sqrt{6}}{5}\)
No podemos tomar la raíz cuadrada de un número negativo. Entonces, cuando sustituimos a, b y c en la Fórmula Cuadrática, si la cantidad dentro del radical es negativa, la ecuación cuadrática no tiene una solución real. Esto lo veremos en el siguiente ejemplo.
Resuelve\(3p^2+2p+9=0\) usando la Fórmula Cuadrática.
- Contestar
-
Esta ecuación está en forma estándar. 
Identificar los valores a, b, c. 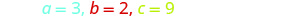
Escribe la Fórmula Cuadrática. 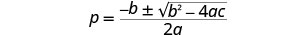
Después sustituya en los valores de a, b, c. 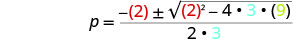
Simplificar. 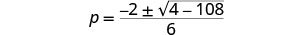
Simplifica lo radical. 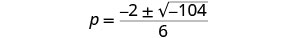
No podemos tomar la raíz cuadrada de un número negativo. No hay una solución real.
Resuelve\(4a^2−3a+8=0\) usando la Fórmula Cuadrática.
- Contestar
-
ninguna solución real
Resuelve\(5b^2+2b+4=0\) usando la Fórmula Cuadrática.
- Contestar
-
ninguna solución real
Las ecuaciones cuadráticas que hemos resuelto hasta ahora en esta sección fueron todas escritas en forma estándar,\(ax^2+bx+c=0\). A veces, tendremos que hacer algo de álgebra para obtener la ecuación en forma estándar antes de poder usar la Fórmula Cuadrática.
Resuelve\(x(x+6)+4=0\) usando la Fórmula Cuadrática.
- Contestar
-

Distribuir para obtener la ecuación en forma estándar. 
Esta ecuación se encuentra ahora en forma estándar. 
Identificar los valores a, b, c. 
Escribe la Fórmula Cuadrática. 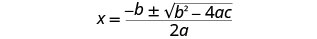
Después sustituya en los valores de a, b, c. 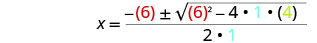
Simplificar. 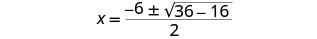
Simplifica dentro del radical. 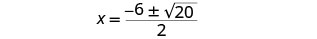
Simplifica lo radical. 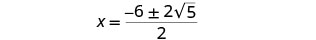
Facturar el factor común en el numerador. 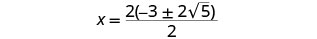
Eliminar los factores comunes. 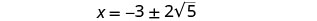
Reescribe para mostrar dos soluciones. 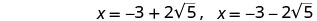
Cheque. Te dejamos el cheque a ti.
Resuelve\(x(x+2)−5=0\) usando la Fórmula Cuadrática.
- Contestar
-
\(x=−1\pm\sqrt{6}\)
Resuelve\(y(3y−1)−2=0\) usando la Fórmula Cuadrática.
- Contestar
-
\(y=−\frac{2}{3}\),\(y=1\)
Cuando resolvimos ecuaciones lineales, si una ecuación tenía demasiadas fracciones, 'eliminamos las fracciones' multiplicando ambos lados de la ecuación por la LCD. Esto nos dio una ecuación equivalente —sin fracciones— para resolver. Podemos usar la misma estrategia con ecuaciones cuadráticas.
Resuelve\(\frac{1}{2}u^2+\frac{2}{3}u=\frac{1}{3}\) usando la Fórmula Cuadrática.
- Contestar
-
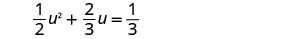
Multiplica ambos lados por la pantalla LCD, 6, para borrar las fracciones. 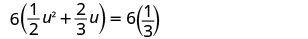
Multiplicar. 
Restar 2 para obtener la ecuación en forma estándar. 
Identificar los valores a, b, c. 
Escribe la Fórmula Cuadrática. 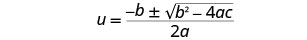
Después sustituya en los valores de a, b, c. 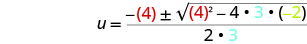
Simplificar. 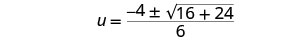
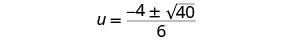
Simplifica lo radical. 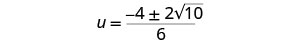
Facturar el factor común en el numerador. 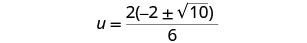
Eliminar los factores comunes. 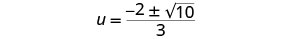
Reescribe para mostrar dos soluciones. 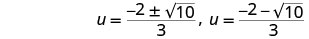
Cheque. Te dejamos el cheque a ti.
Resuelve\(\frac{1}{4}c^2−\frac{1}{3}c=\frac{1}{12}\) usando la Fórmula Cuadrática.
- Contestar
-
\(c=\frac{2\pm\sqrt{7}}{3}\)
Resuelve\(\frac{1}{9}d^2−\frac{1}{2}d=−\frac{1}{2}\) usando la Fórmula Cuadrática.
- Contestar
-
\(d=\frac{3}{2}\),\(d=3\)
Piensa en la ecuación\((x−3)^2=0\). We know from the Zero Products Principle that this equation has only one solution: \(x=3\).
Veremos en el siguiente ejemplo cómo usar la Fórmula Cuadrática para resolver una ecuación con un cuadrado perfecto también da solo una solución.
Resuelve\(4x^2−20x=−25\) usando la Fórmula Cuadrática.
- Contestar
-

Agrega 25 para obtener la ecuación en forma estándar. 
Identificar los valores a, b, c. 
Escribe la Fórmula Cuadrática. 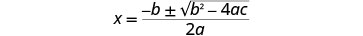
Después sustituya en los valores de a, b, c. 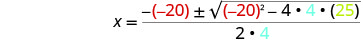
Simplificar. 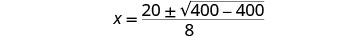
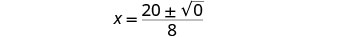
Simplifica lo radical. 
Simplifica la fracción. 
Cheque. Te dejamos el cheque a ti. ¿Reconoció que\(4x^2−20x+25\) es un cuadrado perfecto?
Resuelve\(r^2+10r+25=0\) usando la Fórmula Cuadrática.
- Contestar
-
\(r=−5\)
Resuelve\(25t^2−40t=−16\) usando la Fórmula Cuadrática.
- Contestar
-
\(t=\frac{4}{5}\)
Utilizar el discriminante para predecir el número de soluciones de una ecuación cuadrática
Cuando resolvimos las ecuaciones cuadráticas en los ejemplos anteriores, a veces obtuvimos dos soluciones, a veces una solución, a veces ninguna solución real. ¿Hay alguna manera de predecir el número de soluciones a una ecuación cuadrática sin resolver realmente la ecuación?
Sí, la cantidad dentro del radical de la Fórmula Cuadrática nos facilita determinar el número de soluciones. Esta cantidad se llama el discriminante.
En la Fórmula Cuadrática\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\), la cantidad\(b^2−4ac\) se llama discriminante.
Veamos el discriminante de las ecuaciones en Ejemplo, Ejemplo y Ejemplo, y el número de soluciones a esas ecuaciones cuadráticas.
| Ecuación cuadrática (en forma estándar) | Discriminante\(b^2−4ac\) | Signo del discriminante | Número de soluciones reales | |
|---|---|---|---|---|
| Ejemplo | \(2x^2+9x−5=0\) | \ (b^2−4ac\)” data-valign="middle” class="lt-math-15194">\(9^2−4·2(−5)=121\) | + | 2 |
| Ejemplo | \(4x^2−20x+25=0\) | \ (b^2−4ac\)” data-valign="middle” class="lt-math-15194">\((−20)^2−4·4·25=0\) | 0 | 1 |
| Ejemplo | \(3p^2+2p+9=0\) | \ (b^2−4ac\)” data-valign="middle” class="lt-math-15194">\(2^2−4·3·9=−104\) | − | 0 |
Cuando el discriminante es positivo\(x=\frac{−b\pm\sqrt{+}}{2a}\) la ecuación cuadrática tiene dos soluciones.
Cuando el discriminante es cero\(x=\frac{−b\pm\sqrt{0}}{2a}\) la ecuación cuadrática tiene una solución.
Cuando el discriminante es negativo\(x=\frac{−b\pm\sqrt{−}}{2a}\) la ecuación cuadrática no tiene soluciones reales.
Para una ecuación cuadrática de la forma\(ax^2+bx+c=0\)\(a \ge 0\),
- si\(b^2−4ac>0\), la ecuación tiene dos soluciones.
- si\(b^2−4ac=0\), la ecuación tiene una solución.
- si\(b^2−4ac<0\), la ecuación no tiene soluciones reales.
Determine el número de soluciones para cada ecuación cuadrática:
- \(2v^2−3v+6=0\)
- \(3x^2+7x−9=0\)
- \(5n^2+n+4=0\)
- \(9y^2−6y+1=0\)
- Contestar
-
1.
\(2v^2−3v+6=0\) La ecuación está en forma estándar, identificar a, b, c. \(a=2\),\(b=−3\),\(c=6\) Escribe el discriminante. \(b^2−4ac\) Sustituto en los valores de a, b, c. \((3)^2−4·2·6\) Simplificar. \(9−48\)
\(−39\)
Debido a que el discriminante es negativo, no hay soluciones reales a la ecuación. 2.
\(3x^2+7x−9=0\) La ecuación está en forma estándar, identificar a, b, c. \(a=3\),\(b=7\),\(c=−9\) Escribe el discriminante. \(b^2−4ac\) Sustituto en los valores de a, b, c. \((7)^2−4·3·(−9)\) Simplificar. \(49+108\)
\(157\)
Debido a que el discriminante es positivo, hay dos soluciones a la ecuación. 3.
\(5n^2+n+4=0\) La ecuación está en forma estándar, identificar a, b, c. \(a=5\),\(b=1\),\(c=4\) Escribe el discriminante. \(b^2−4ac\) Sustituto en los valores de a, b, c. \((1)^2−4·5·4\) Simplificar. \(1−80\)
\(−79\)
Debido a que el discriminante es negativo, no hay soluciones reales a la ecuación. 4.
\(9y^2−6y+1=0\) La ecuación está en forma estándar, identificar a, b, c. \(a=9\),\(b=−6\),\(c=1\) Escribe el discriminante. \(b^2−4ac\) Sustituto en los valores de a, b, c. \((−6)^2−4·9·1\) Simplificar. \(36−36\)
\(0\)
Debido a que el discriminante es 0, hay una solución a la ecuación.
Determine el número de soluciones para cada ecuación cuadrática:
- \(8m^2−3m+6=0\)
- \(5z^2+6z−2=0\)
- \(9w^2+24w+16=0\)
- \(9u^2−2u+4=0\)
- Contestar
-
- no hay soluciones reales
- 2
- 1
- no hay soluciones reales
Determine el número de soluciones para cada ecuación cuadrática:
- \( b^2+7b−13=0\)
- \(5a^2−6a+10=0\)
- \(4r^2−20r+25=0\)
- \(7t^2−11t+3=0\)
- Contestar
-
- 2
- no hay soluciones reales
- 1
- 2
Identificar el método más apropiado para resolver una ecuación cuadrática
Hemos utilizado cuatro métodos para resolver ecuaciones cuadráticas:
- Factoring
- Propiedad Raíz Cuadrada
- Completando la Plaza
- Fórmula cuadrática
Puedes resolver cualquier ecuación cuadrática usando la Fórmula Cuadrática, pero ese no siempre es el método más fácil de usar.
- Pruebe Factoring primero. Si los factores cuadráticos fácilmente, este método es muy rápido.
- Pruebe la propiedad de raíz cuadrada a continuación. Si la ecuación se ajusta a la forma\(ax^2=k\) o\(a(x−h)^2=k\), se puede resolver fácilmente usando la Propiedad Raíz Cuadrada.
- Usa la Fórmula Cuadrática. Cualquier ecuación cuadrática se puede resolver usando la Fórmula Cuadrática.
¿Y el método para completar la plaza? A la mayoría de la gente le resulta engorroso ese método y prefiere no usarlo. Necesitábamos incluirlo en este capítulo porque terminamos la plaza en general para derivar la Fórmula Cuadrática. También utilizarás el proceso de completar el cuadrado en otras áreas del álgebra.
Identificar el método más adecuado a utilizar para resolver cada ecuación cuadrática:
- \(5z^2=17\)
- \(4x^2−12x+9=0\)
- \(8u^2+6u=11\)
- Contestar
-
1. \(5z^2=17\)
Dado que la ecuación está en el\(ax^2=k\), el método más apropiado es usar la Propiedad Raíz Cuadrada.
2. \(4x^2−12x+9=0\)
Reconocemos que el lado izquierdo de la ecuación es un trinomio cuadrado perfecto, por lo que Factoring será el método más apropiado.
3. \(8u^2+6u=11\)
Poner la ecuación en forma estándar. \(8u^2+6u−11=0\)
Si bien nuestro primer pensamiento puede ser probar Factoring, pensar en todas las posibilidades de prueba y error nos lleva a elegir la Fórmula Cuadrática como el método más apropiado.
Identificar el método más adecuado a utilizar para resolver cada ecuación cuadrática:
- \(x^2+6x+8=0\)
- \((n−3)^2=16\)
- \(5p^2−6p=9\)
- Contestar
-
- factor
- Propiedad Raíz Cuadrada
- Fórmula cuadrática
Identificar el método más adecuado a utilizar para resolver cada ecuación cuadrática:
- \(8a^2+3a−9=0\)
- \(4b^2+4b+1=0\)
- \(5c2=125\)
- Contestar
-
- Fórmula cuadrática
- factorización
- Propiedad Raíz Cuadrada
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con el uso de la Fórmula Cuadrática:
- Resolver ecuaciones cuadráticas: Resolver con la fórmula cuadrática
- Cómo resolver una ecuación cuadrática en forma estándar usando la Fórmula Cuadrática (ejemplo)
- Resolver ecuaciones cuadráticas usando la fórmula cuadrática—Ejemplo 3
- Resolver ecuaciones cuadráticas usando fórmula cuadrática
Conceptos clave
- Fórmula cuadrática Las soluciones a una ecuación cuadrática de la forma\(ax^2+bx+c=0\),\(a \ge 0\) vienen dadas por la fórmula:
\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\)
- Resolver una Ecuación Cuadrática Usando la Fórmula Cuadrática
Para resolver una ecuación cuadrática usando la Fórmula Cuadrática.- Escribe la fórmula cuadrática en forma estándar. Identificar los valores a, b, c.
- Escribe la fórmula cuadrática. Después sustituya en los valores de a, b, c.
- Simplificar.
- Consulta las soluciones.
- Uso del discriminante,\(b^2−4ac\), para determinar el número de soluciones de una ecuación cuadrática
Para una ecuación cuadrática de la forma\(ax^2+bx+c=0\),\(a \ge 0\),- si\(b^2−4ac>0\), la ecuación tiene 2 soluciones.
- si\(b^2−4ac=0\), la ecuación tiene 1 solución.
- si\(b^2−4ac<0\), la ecuación no tiene soluciones reales.
- Para identificar el método más adecuado para resolver una ecuación cuadrática:
- Pruebe Factoring primero. Si los factores cuadráticos fácilmente este método es muy rápido.
- Pruebe la propiedad de raíz cuadrada a continuación. Si la ecuación se ajusta a la forma\(ax^2=k\) o\(a(x−h)^2=k\), se puede resolver fácilmente usando la Propiedad Raíz Cuadrada.
- Usa la Fórmula Cuadrática. Cualquier otra ecuación cuadrática se resuelve mejor usando la Fórmula Cuadrática.
Glosario
- discriminante
- En la Fórmula Cuadrática,\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\) la cantidad\(b^2−4ac\) se llama discriminante.


