4.2: Dominio y rango de una función

El análisis del comportamiento de las funciones aborda cuestiones de cuándo la función está aumentando o disminuyendo, si y dónde tiene valores máximos o mínimos, dónde cruza el$y$ eje$x$ o, y qué valores de$x$ y$y$ se van a incluir en la función.

El conjunto de valores disponibles para la variable$x,$ o independiente se llama Dominio de la función. El conjunto de$y$ valores correspondientes se llama Rango de la función.

La función lineal mencionada anteriormente$f(x)=6 x-1$ tiene un dominio de todos los números reales y un rango de todos los números reales,$x \in \mathbb{R}$ y$y \in \mathbb{R}$. Por otra parte, la función$f(x)=x^{2}$ tiene un dominio de todos los números reales,$x \in \mathbb{R},$ pero su rango se limita a los números reales positivos,$y \geq 0$

Las consideraciones del dominio de una función suelen referirse a restricciones sobre las cuales$x$ los valores generarán valores de número real para$y .$ Las restricciones más comunes ocurren con el uso de funciones de raíz cuadrada o funciones racionales.

El dominio de la función$f(x)=\sqrt{x-7}$ sería el conjunto de$x \geq 7,$ para que no se permitan valores negativos bajo la raíz cuadrada. Esto asegura los valores reales necesarios para$y .$ El rango para esta función es$y \geq 0$

El dominio de la función$f(x)=\frac{x}{2 x-3}$ sería$x \in \mathbb{R}$ (todos los números reales), pero evitando$x \neq \frac{3}{2},$ así un denominador cero que es un valor indefinido. El rango para esta función sería$y \in \mathbb{R}$ (todos los números reales), pero$y \neq \frac{1}{2},$ debido a la asíntota horizontal en$y=\frac{1}{2}$

Las cuestiones de dominio y rango se vuelven más interesantes cuando se consideran en relación con funciones definidas por gráficas, o en aplicaciones. En una aplicación que involucra perímetro en la que el perímetro de un rectángulo se da como 50 pies, sabemos que
\ [
2\ ell+2 w=50
\]
Reescribiendo esto en función de$w,$ podemos decir que
\ [
\ ell=f (w) =25-w
\ ]

En esta función relacionando el largo y ancho en base a un perímetro dado, podemos decir que el dominio de la función es$0<w<25 .$ El ancho debe ser mayor que 0 pero menor que de$25,$ otra manera no habría un rectángulo. Lo mismo es cierto para el rango o posible conjunto de valores para la longitud$0<\ell<25$ Ejercicios 4.2
Encuentra el dominio y el rango para cada una de las siguientes funciones:
1)$\quad f(x)=\sqrt{2 x+1}$
2)$\quad f(x)=\sqrt{3 x-5}$
3)$\quad \frac{x}{x+9}$
4)$\quad f(x)=\frac{x+2}{2 x-3}$
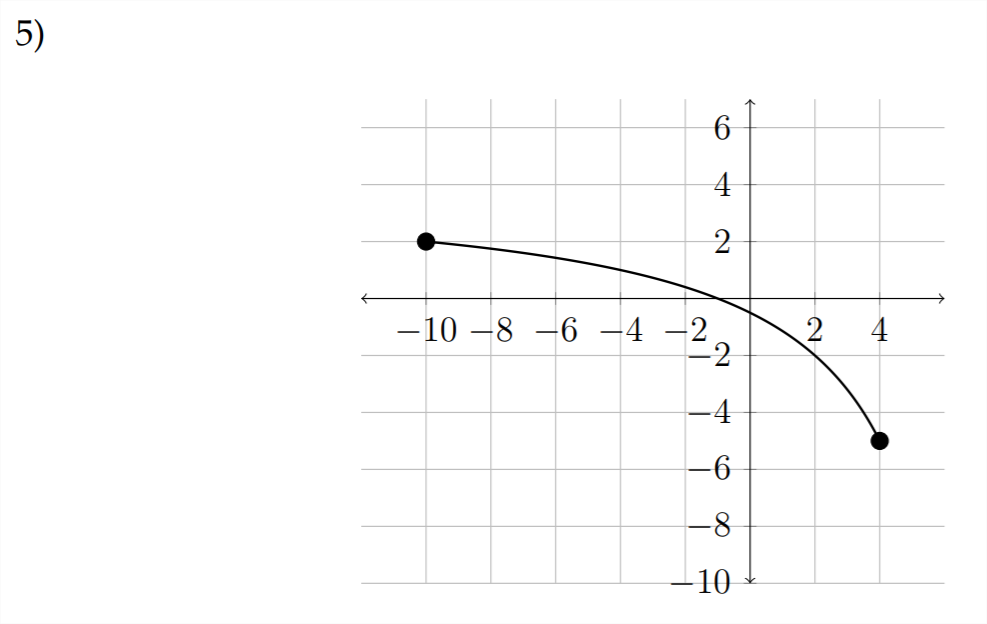
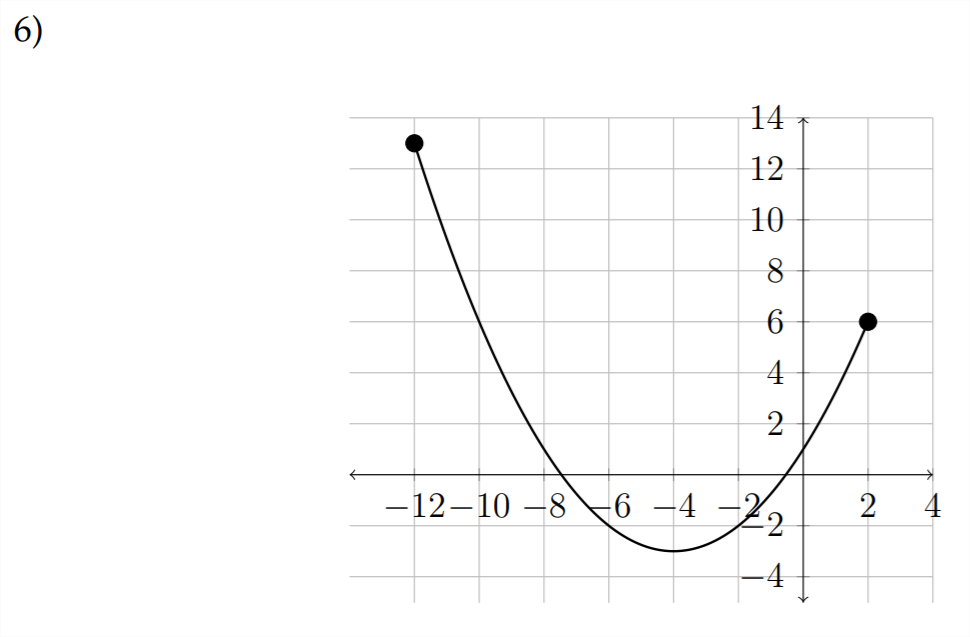
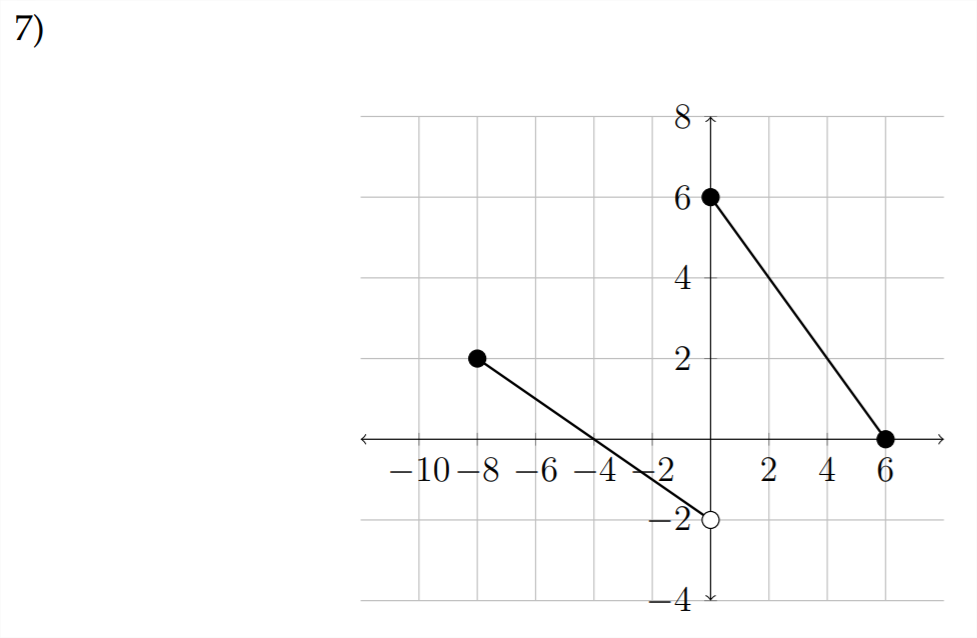
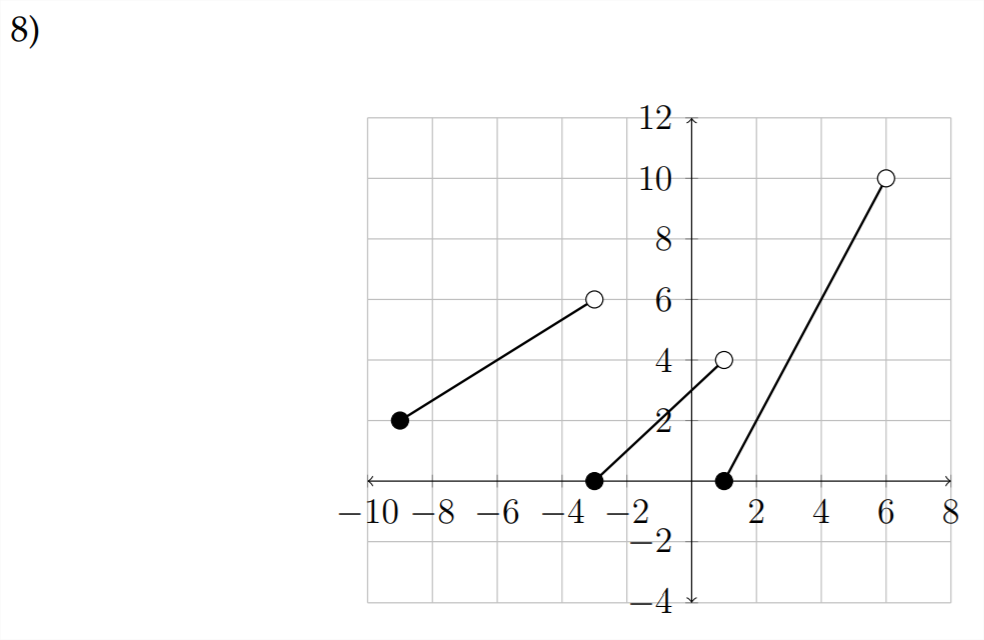
Para las siguientes gráficas, supongamos que los puntos finales para el dominio y el rango son números enteros.