4.4: Transformaciones

Última actualización
Guardar como PDF

Page ID: 111928

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hay tres tipos principales de transformación que consideraremos:
1) Desplazamientos horizontales y verticales
2) Reflexiones sobre el$y$ eje$x$ o
3) Estiramientos horizontales y verticales
Si tomamos una función dada, digamos$f(x)=x,$ entonces esto tiene la gráfica que vemos a continuación - una línea recta con una pendiente de 1 y una$y$ -intercepción de$0 .$ Si agregamos a la función$f(x)+6=x+6,$ entonces esto agregará 6 a todos los$y$ -valores que desplaza la gráfica 6 lugares hacia arriba.

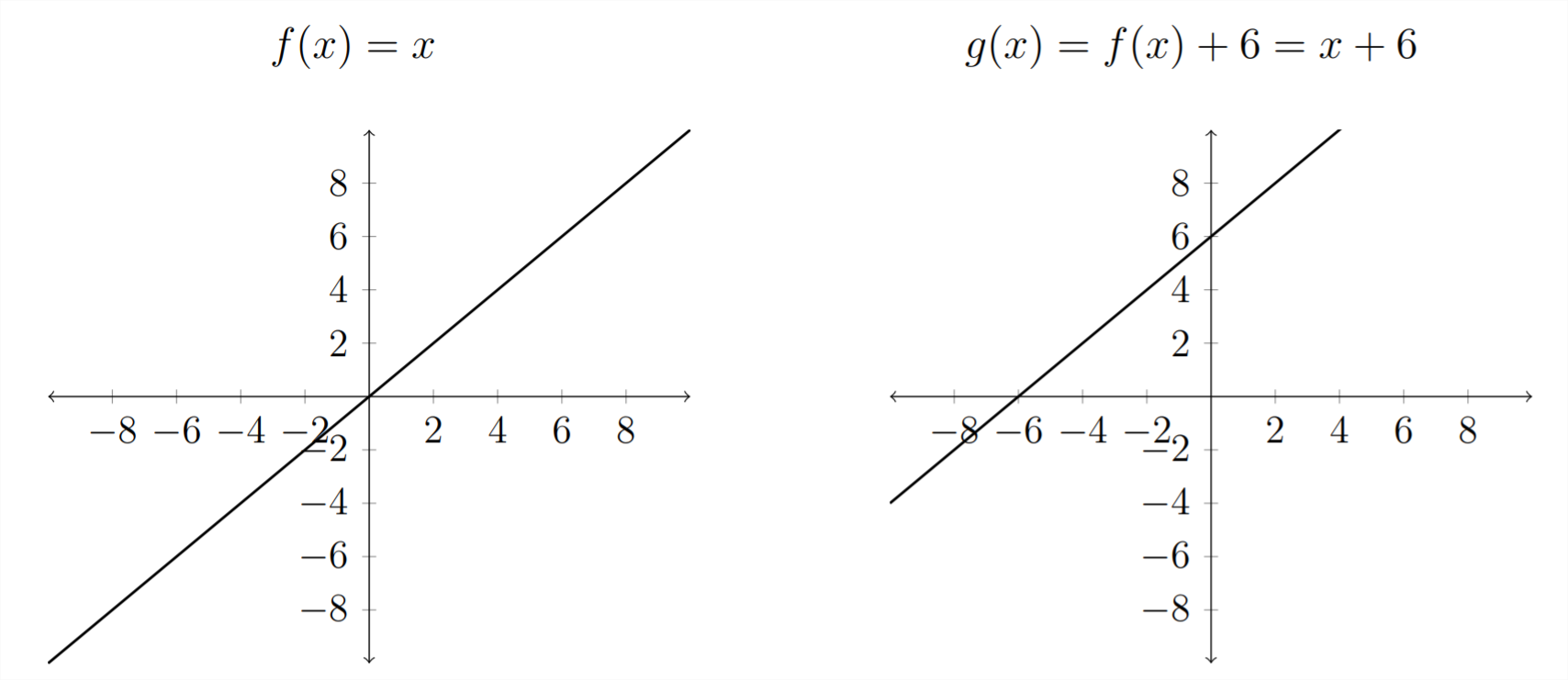
$clipboard_edb94f846b02456aeaf26cb9d5d4ae93a.png$

Desplazamientos verticales
Entonces, si tenemos una función general$f(x)$ que es descrita por una gráfica, podemos determinar una gráfica para$f(x)+k,$ donde$k$ está algún número que ya sea desplazará hacia$f(x)$ arriba$(\text { if } k>0)$ o hacia abajo (si$k<0$)
Por ejemplo, considere el siguiente gráfico para$f(x)$
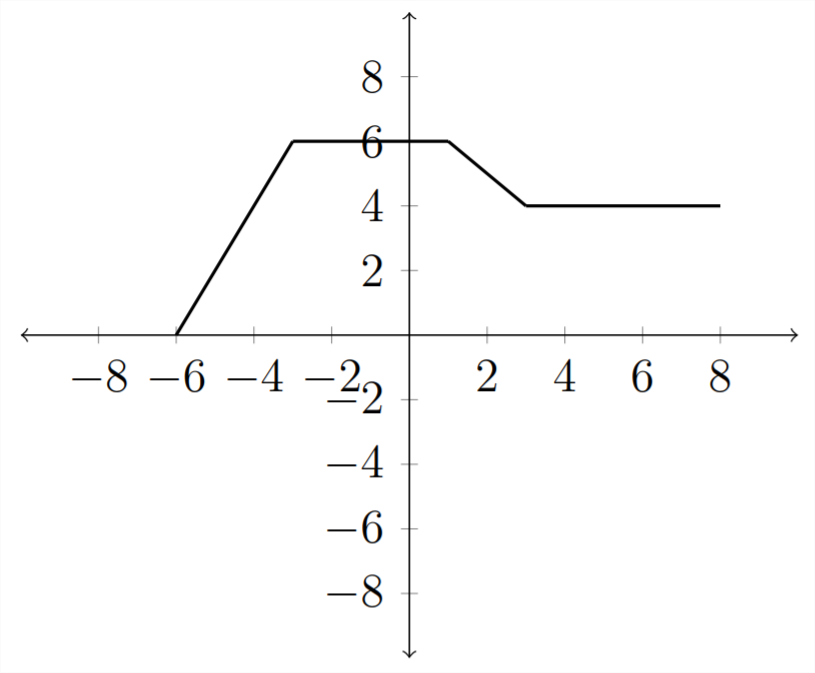
$clipboard_e1868c85fac715e9cc59d36869608e752.png$

Entonces, si queremos una gráfica para$f(x)-2$, simplemente desplaza todos los$y$ -valores hacia abajo 2 lugares:
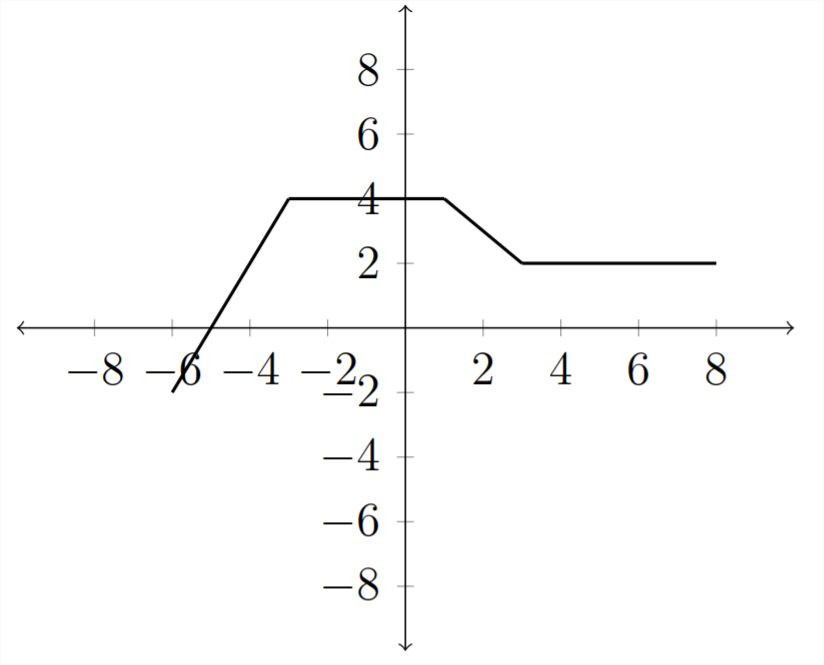
$clipboard_e384d64a193e49d8d61bd23533e44a9c5.png$
Esta es una transformación de desplazamiento vertical estándar de una función.

Desplazamientos horizontales
Una función también se puede desplazar horizontalmente sumando o restando un número dentro de los paréntesis.
Si empezamos con nuestra función original$f(x)$
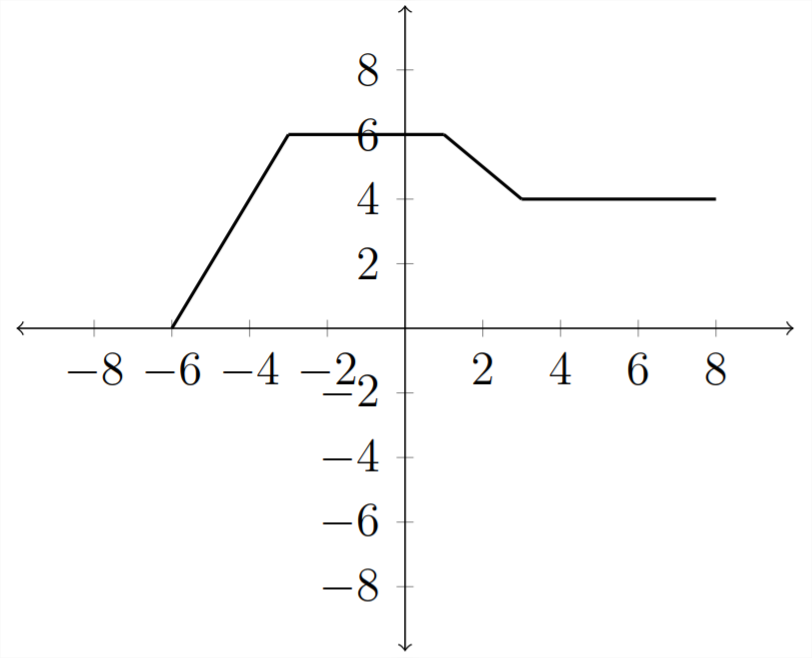
$clipboard_e0a58a36da1538d0151b00fc036bc5f2b.png$

Entonces la transformación$f(x-2)$ desplazará la gráfica horizontalmente, excepto que se moverá en sentido contrario al signo. El$f(x-2)$ turno moverá la gráfica 2 lugares a la derecha mientras que un desplazamiento de$f(x+2)$ moverá la gráfica 2 lugares a la izquierda.

La razón por la que esto sucede será más clara si miramos una tabla de valores para la función:
$clipboard_e3f5d56400b176ab907f8f40093fbc2c3.png$
Ahora, si, en lugar de$f(x),$ queremos$f(x-2),$ entonces agregamos otra columna a la tabla:
$clipboard_e6edd92e2223e347c7bfb6507c763b105.png$
Observe que para tener la misma$y$ -valor como la gráfica original, debemos ir 2 lugares a la derecha para que después de restar 2 del$x$ -valor, lleguemos de nuevo al$x$ -valor original. Entonces la gráfica de$f(x-2)$ se verá así:
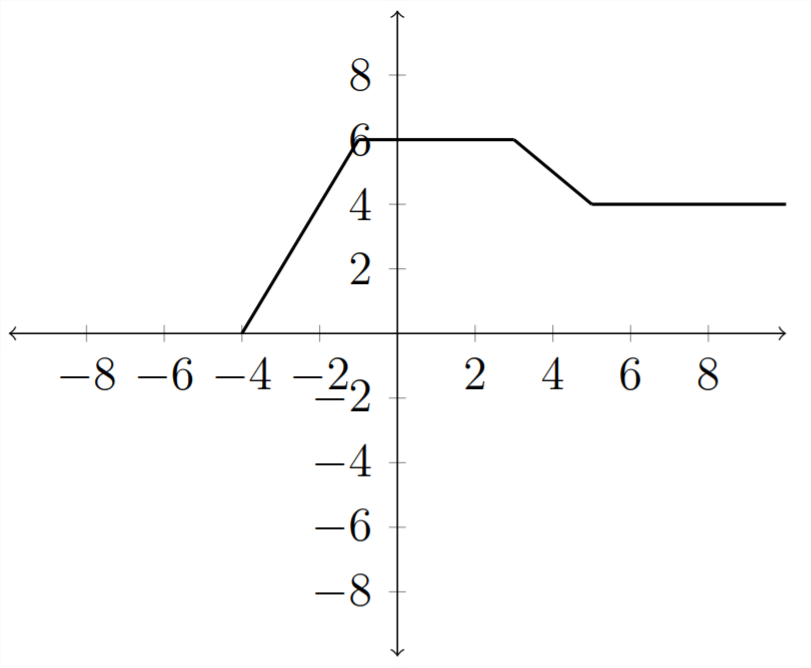
$clipboard_e7ab3b4b08959c213634cd486b7c18eb4.png$
Observe cómo los valores en la gráfica coinciden con los valores de la tabla.

Reflexiones La
negación de$y$ los valores$x$ o de una función tendrá el efecto de reflejar la función sobre el$x$ eje$y$ o. Si consideramos la función$f(x)$ - la misma que usamos en los ejemplos anteriores:
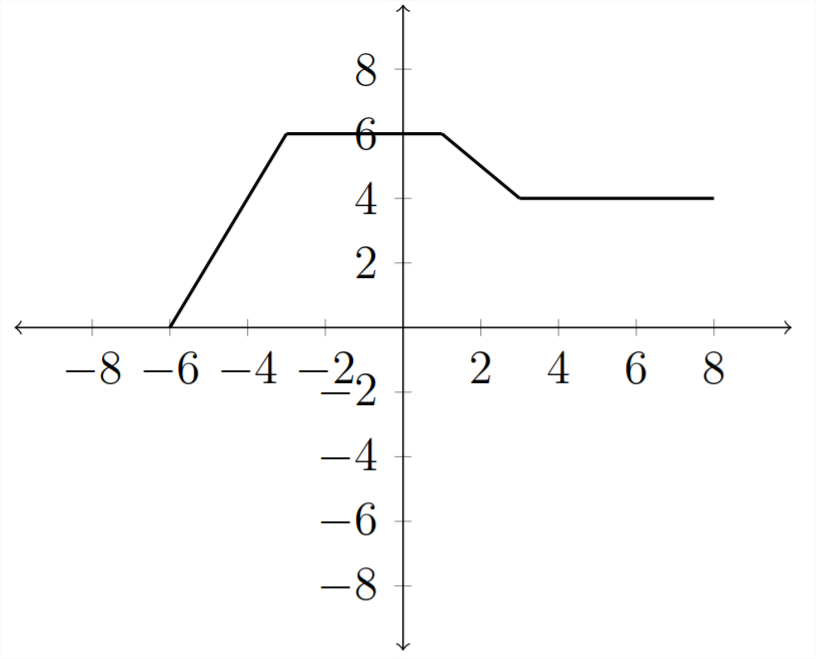
$clipboard_e347cd8db4203bc3a2a618eccde38de61.png$
Entonces la gráfica de se$y=-f(x)$ reflejará sobre el$x$ eje -eje. El signo negativo frente a la función niega todos los$y$ valores, reflejándolos sobre el$x$ eje. Veamos esto en una tabla de valores:
$clipboard_e9dd6028bd7beb4188d4eec9848e996bf.png$
Entonces la gráfica se vería así:
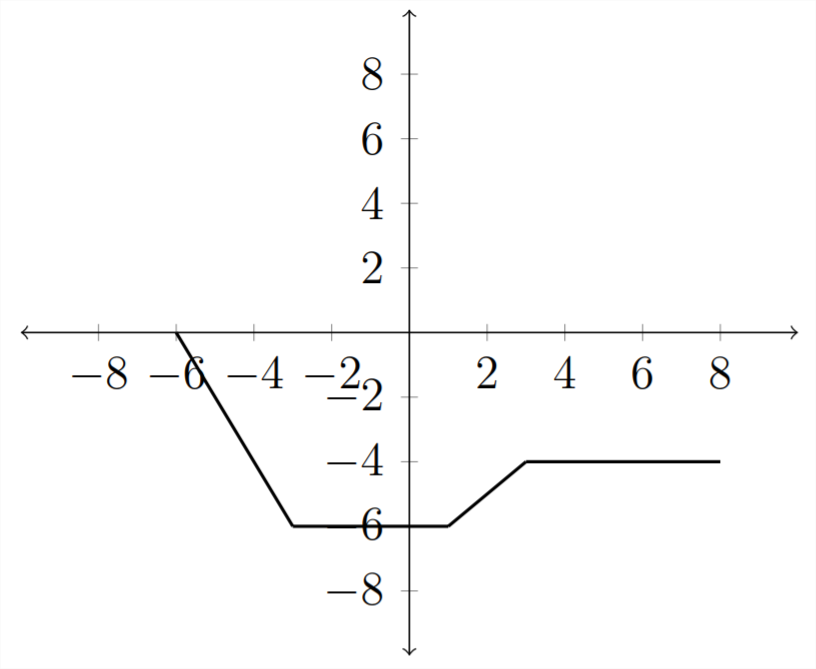
$clipboard_ec75725e96bda259ad5fbe6e863659f51.png$
Por otro lado, si negamos la$x$ variable$(f(-x)),$ -entonces los valores de la función previamente asociados con los valores positivos de $x$estaría asociado con los valores negativos de$x$ y viceversa. Esto reflejaría la función sobre el$y$ eje -eje.
Si volvemos a considerar nuestra función original y una tabla de valores:
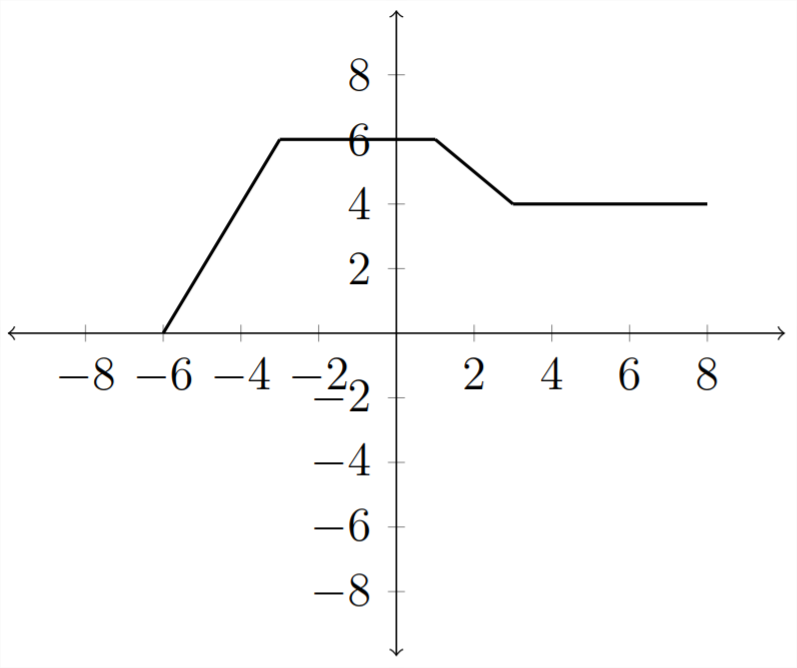
$clipboard_e64f52485364cf255f8cc8ba15f4f0fdb.png$
En la tabla:
$clipboard_e0ab871f54621ac5390d031306b8528ef.png$
Y la gráfica se reflejaría sobre el$y$ eje -eje:
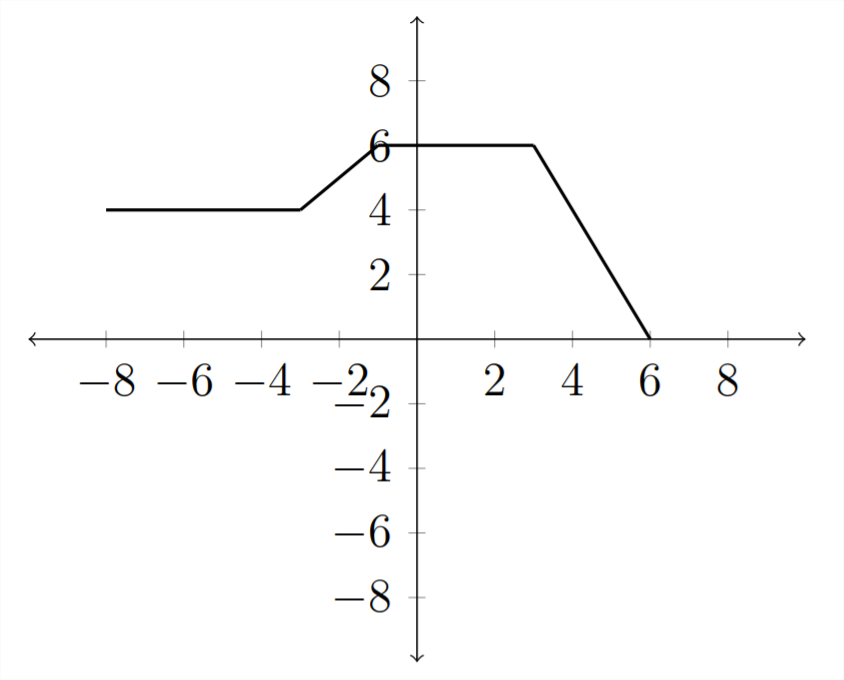
$clipboard_e6c4501bcd8113f99eba11ba445467c0d.png$

Estiramiento y compresión de gráficos

El último tipo de transformación que examinaremos es el de estirar o comprimir una gráfica multiplicando dentro o fuera de los paréntesis. Comenzando con nuestra función de ejemplo familiar$y=f(x)$
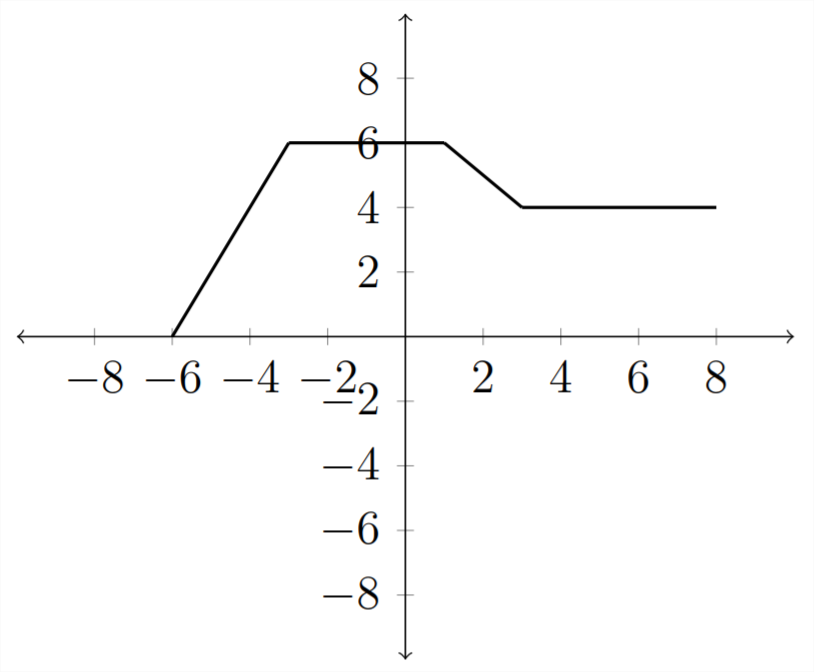
$clipboard_ee635edba8ef54a89bb7811cb6c266823.png$
Si multiplicamos la función por una constante fuera de los paréntesis:$y=2 f(x)$ entonces esto tendrá el efecto de multiplicar todos los$y$ valores por$2 .$ En la tabla:
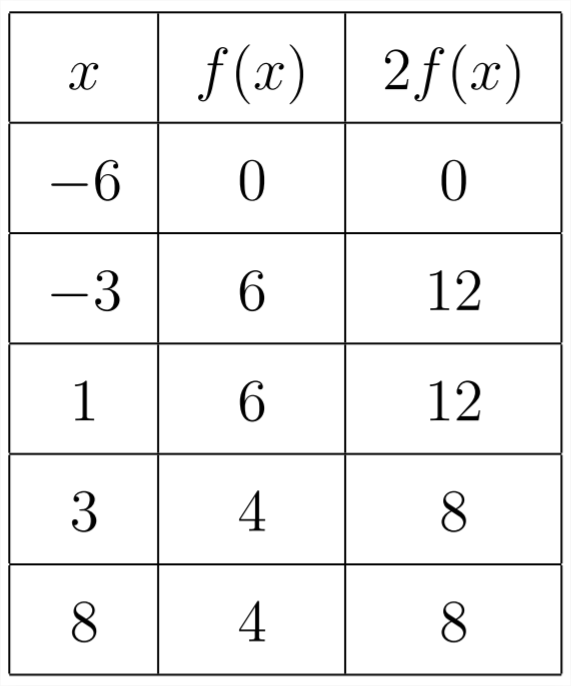
$clipboard_e21f2103671930d6dda497ea205cadf67.png$

La gráfica de se$y=2 f(x)$ vería así:
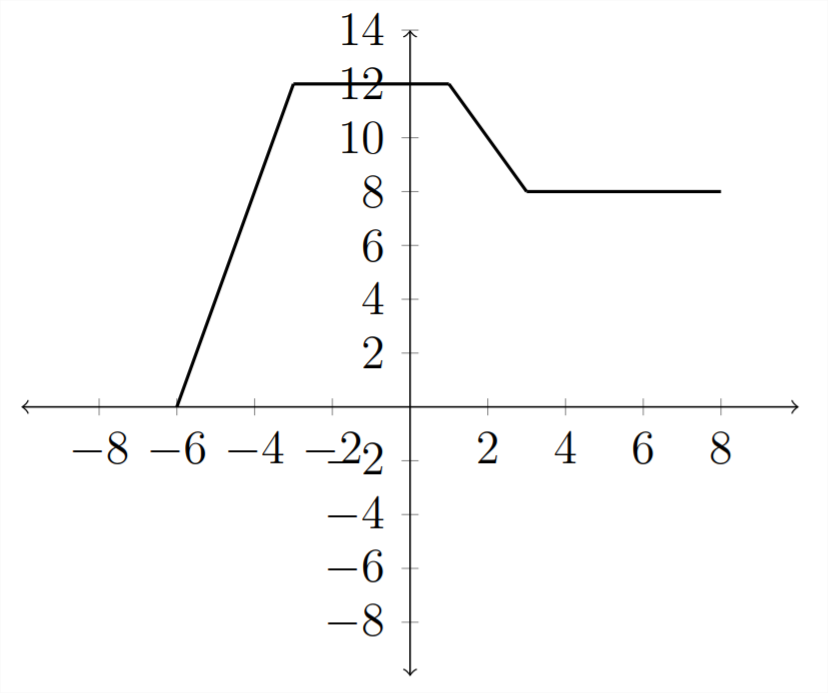
$clipboard_e921e2a2750a616f22f39cb90a3920425.png$
De manera similar, multiplicar por un número menor a 1 comprimiría la gráfica. La gráfica para$y=\frac{1}{2} f(x)$ está a continuación:
$clipboard_e25e17cc193f3365e2d03e6efdf81864a.png$

La multiplicación dentro de los paréntesis afecta a las$x$ variables.
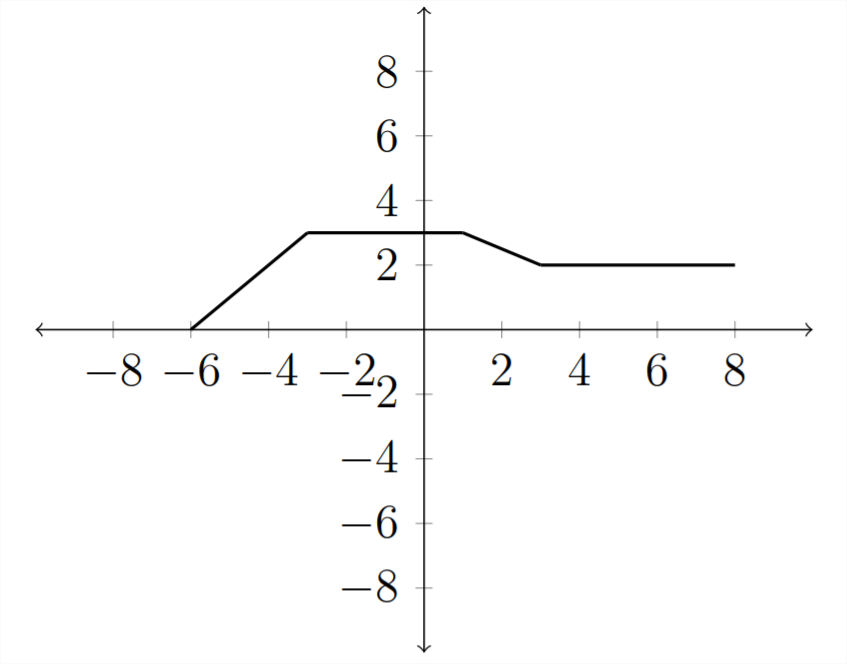
Si consideramos la función$y=f(2 x)$, entonces esto tendrá el efecto de comprimir la gráfica a lo largo del$x$ eje -axis:
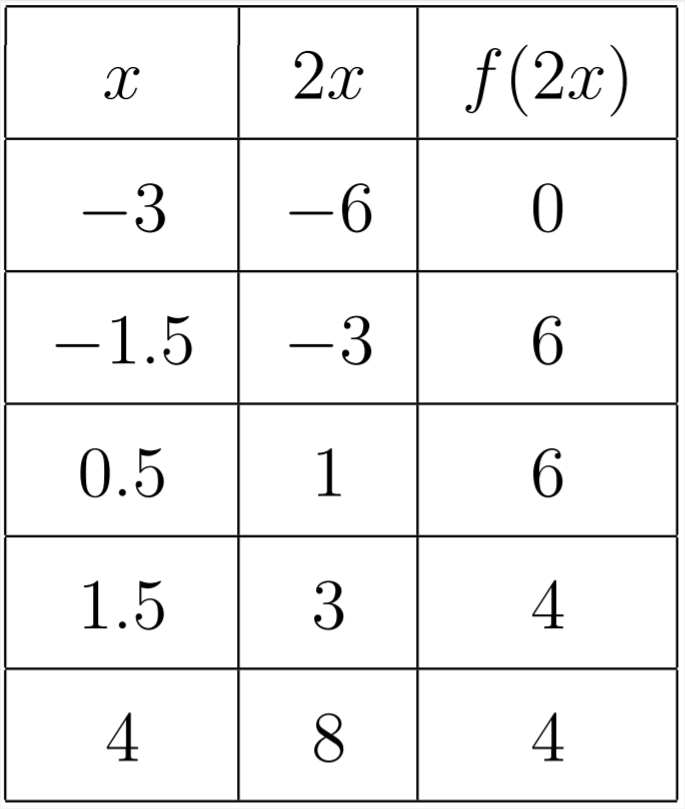
$clipboard_ef614db647c95609a575f1342bfd8177a.png$

Observe cómo cada$x$ valor tuvo que ser cortado a la mitad para que cuando lo multiplicamos por 2 terminemos con el$x$ valor original. La gráfica se vería así:

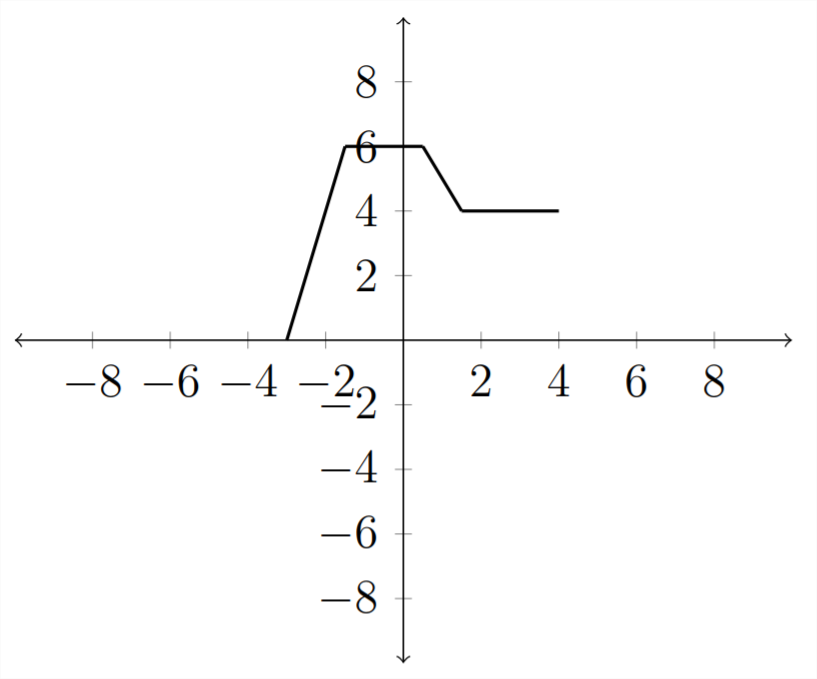
$clipboard_e61bc69029c85ba4a1b495259129bcf73.png$

Multiplicar dentro de los paréntesis por un número menor que uno estiraría la gráfica.
$clipboard_e0e8e7f6a564fce4a37dca0e019782025.png$
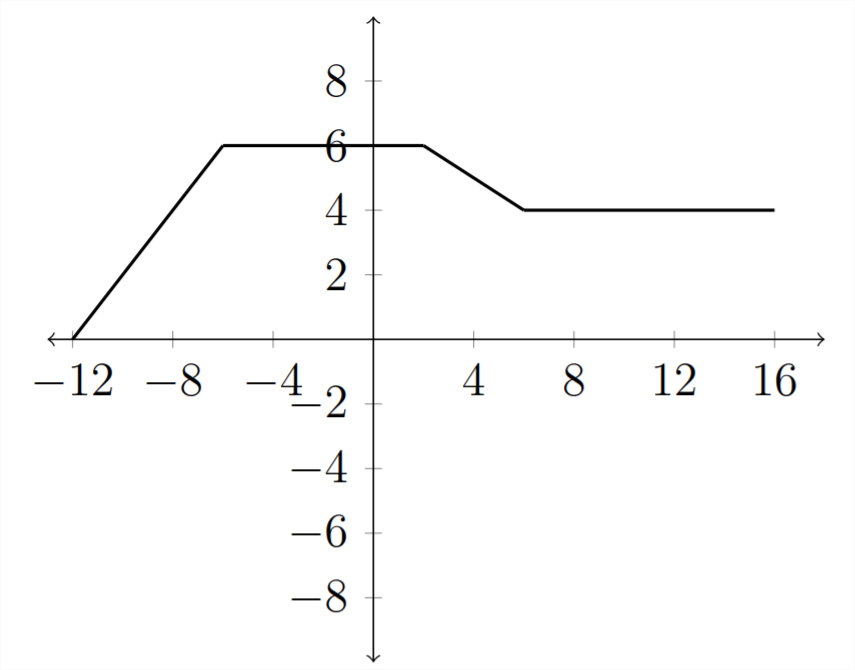
$clipboard_ef9392f4aa2d448f5c2b1adaec789aca2.png$
En estos ejemplos, solo hemos considerado una transformación a la vez. En los ejercicios deberás considerar el efecto de varias transformaciones a la vez.

Ejercicios 4.4
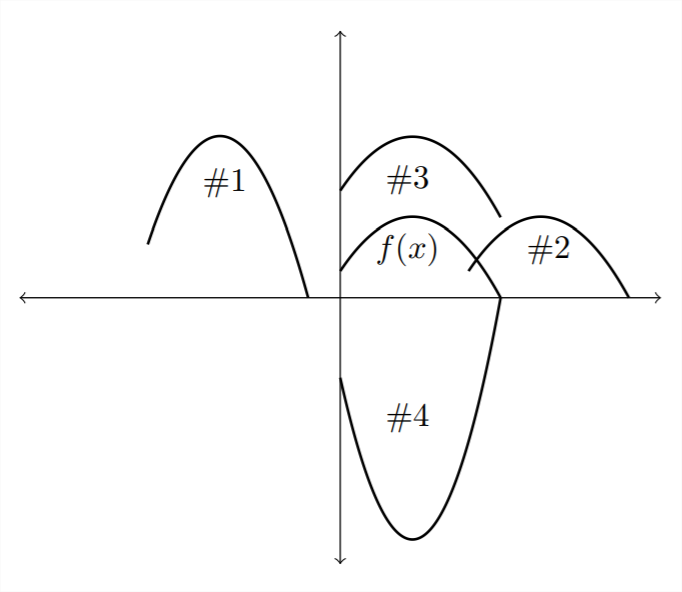
1) Emparejar cada una de las funciones de la gráfica con la transformación apropiada que se describe a continuación.
a)$\quad f(x-4)$
b)$\quad f(x)+3$
c)$\quad -3 f(x)$
d)$\quad 2 f(x+6)$

$clipboard_e167d20f9d1498a9c40e7d33d1e23d22b.png$

2) Coincidir cada una de las descripciones con la transformación de función apropiada.

\ begin {array} {cc}
a)\ quad y=f (x-1) & 1)\ text {Desplazar a la izquierda una unidad}\\
b)\ quad y=f (x) -1 y 2)\ text {Reflejar sobre$x$ -eje, luego desplazar a la izquierda una unidad}\\
c)\ quad y=f (x) +1 y 3)\ text {Desplazar a la derecha una unidad}\\
d)\ quad y=f (x+1) y 4) \ text {Reflejar sobre$x$ -eje, luego desplazar hacia arriba una unidad}\\
e)\ quad y=f (-x) +1 y 5)\ text {Reflejar sobre$x$ -eje, luego desplazar hacia abajo una unidad}\\
f)\ quad y=f (-x) -1 & 6)\ text {Desplazar una unidad hacia abajo}\\
g)\ quad y=-f (x) +1 y 7)\ text {Reflejar sobre $x$-eje, reflejar sobre$y$ -eje, luego desplazar hacia arriba una unidad}\\
h)\ quad y=-f (x+1) & 8\ text {Desplazar a la izquierda una unidad, reflejar sobre$y$ -eje, luego desplazar hacia arriba una unidad}\\
i)\ quad y=-f (x) -1) & 9)\ text {Desplazar una unidad hacia arriba}\\
j)\ quad y=f (-x +1) & 10)\ text {Reflejar sobre$y$ -eje, luego desplazar hacia arriba una unidad}\\
k)\ quad y=-f (-x) & 11)\ text {Reflejar sobre$y$ -eje, luego desplazar hacia abajo una unidad}\\
\ end {array}

3) Coincidir cada una de las descripciones con la adecuada transformación de funciones.
\ begin {array} {cc}
a)\ quad y=f (x+2) +3 & 1)\ text {Desplazar a la izquierda 2 unidades, luego bajar 3 unidades}\\
b)\ quad y=f (x+3) +2 & 2)\ text {Desplazar a la izquierda 3 unidades, luego desplazar hacia arriba 2 unidades}\\
c)\ quad y=f (x-2) +3 & 3)\ text {Desplazar a la derecha 3 unidades, luego turno up 2 unidades}\\
d)\ quad y=f (x-2) -3 & 4)\ text {Desplazar a la izquierda 3 unidades, luego cambiar hacia abajo 2 unidades}\\
e)\ quad y=f (x+2) -3 & 5)\ text {Desplazar a la derecha 3 unidades, luego desplazar hacia abajo 2 unidades}\\
f)\ quad y=f (x-3) +2 & 6)\ text {Reflejar sobre el$y$ eje, luego desplazar up 2 unidades}\\
g)\ quad y=f (x-3) -2 & 7)\ text {Reflejar sobre$x$ -eje, luego desplazar a la derecha 2 unidades}\\
h)\ quad y=f (x+3) -2 & 8)\ text {Reflejar sobre$x$ -eje, luego desplazar a la izquierda 2 unidades}\\
i)\ quad y=-f (x+2) & 9)\ text {Desplazar a la izquierda 2 unidades, luego reflejar sobre el$y$ -eje}\\
j)\ quad y=-f (x-2) & 10)\ text {Desplazar a la derecha 2 unidades, luego desplazar hacia arriba 3 unidades}\\
k)\ quad y=f (2-x) & 11)\ text {Desplazar a la izquierda 2 unidades, luego desplazar hacia arriba 3 unidades}\\
\ ell)\ quad y=f (-x) +2 & 12)\ text {Desplazar a la derecha 2 unidades, luego desplazar hacia abajo 3 unidades}
\ end {array}

Aplicar las transformaciones indicadas para cada función.
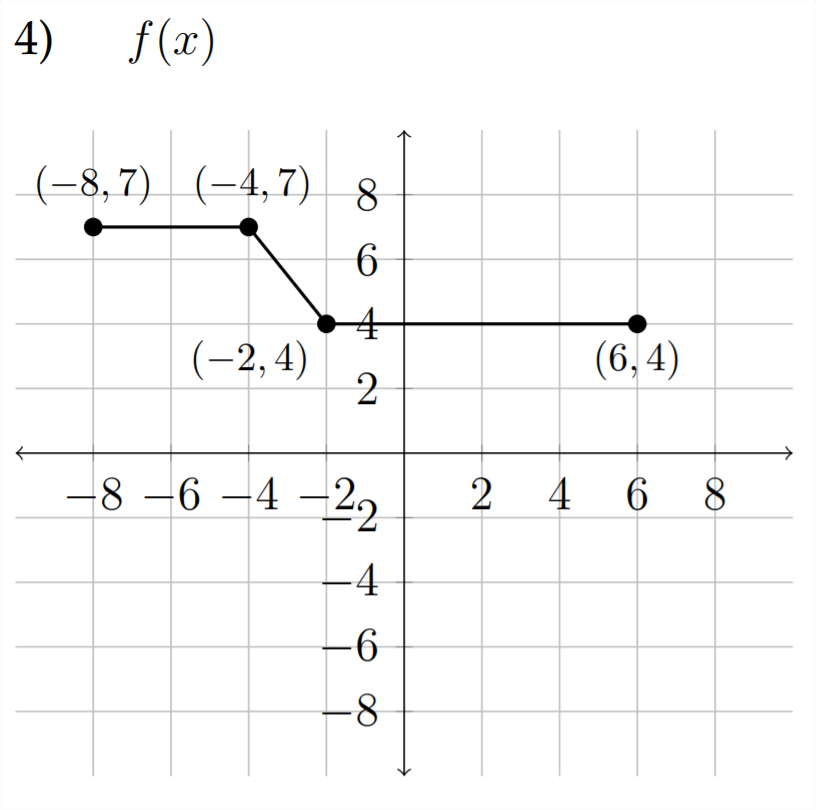
$clipboard_e763571b89dd30538d95b384b10a4bdf0.png$
a)$\quad f(x-3)$
b)$\quad-f(x)+2$
c)$\quad \frac{1}{2} f(x-1)$
d)$\quad f(-x)+1$
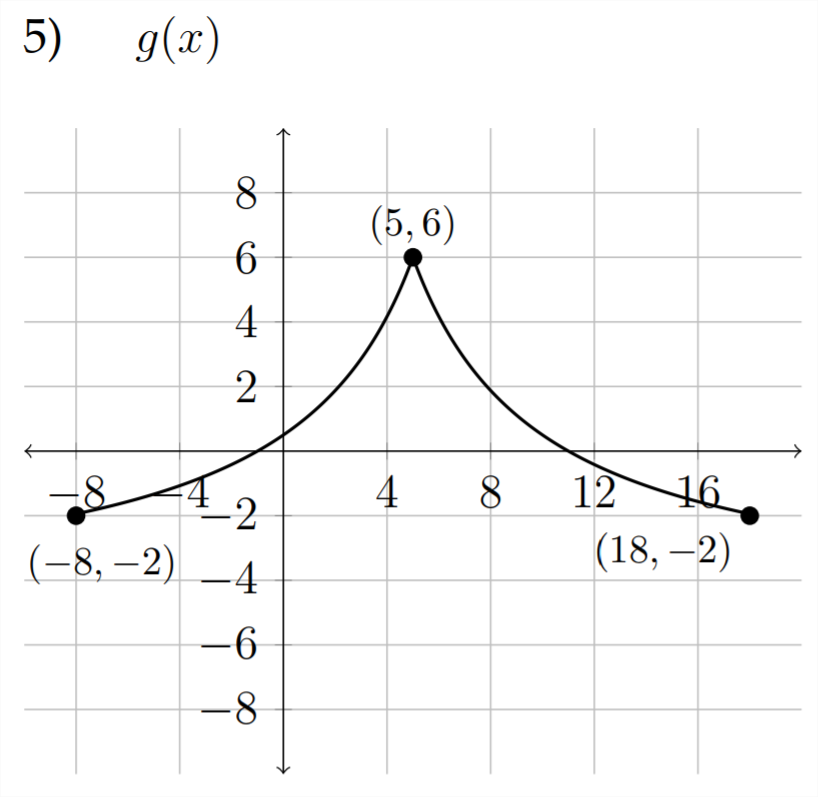
$clipboard_eaf108e96da326bd505a70cda92c9e49e.png$
a)$\quad g(x)-3$
b)$\quad-g(x)-1$
c)$\quad 2 g(x+2)$
d)$\quad g(2 x)-1$
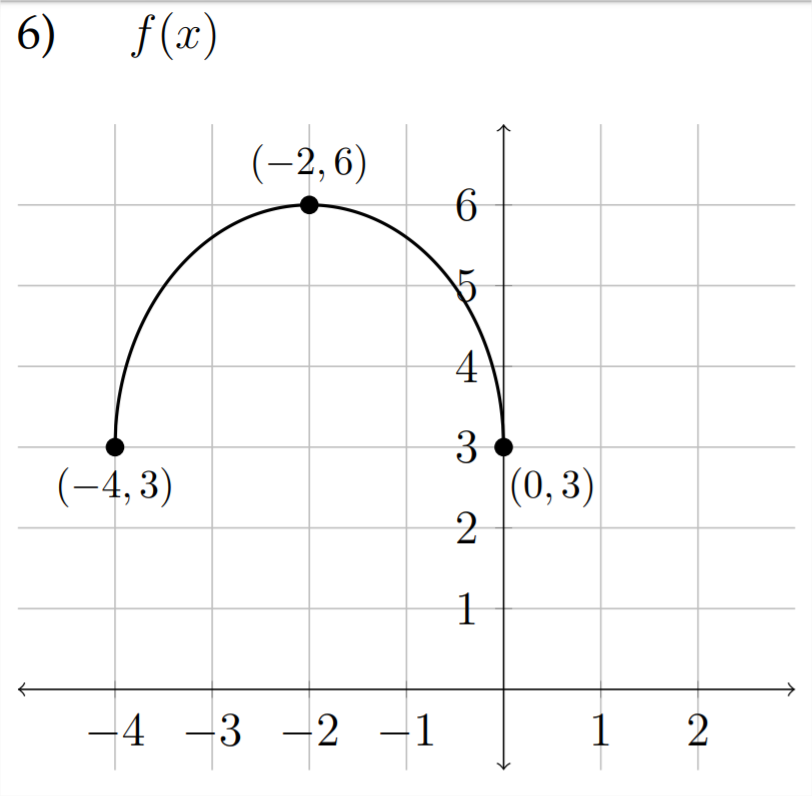
$clipboard_e7a2a4c14187e997b81b319f93be1f797.png$
a)$\quad f(x)+2$
b)$\quad-f(x-1)$
c)$\quad f(x-1)-3$
d)$\quad \frac{1}{3} f(x)+4$

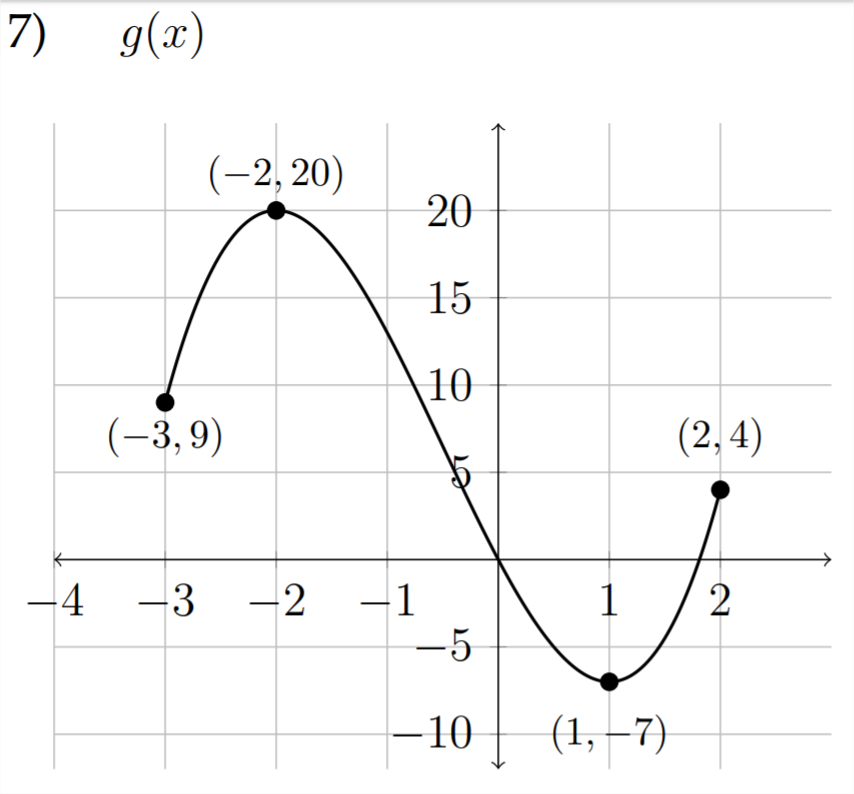
$clipboard_ef971dd6033506d049e078dd2bfd9ee88.png$
a)$\quad g(x-2)$
b)$\quad-g(x)+1$
c)$\quad 2 g(x-1)$
d)$\quad \frac{1}{2} g(x)-3$