4.9: Optimización

Última actualización
Guardar como PDF

Page ID: 111927

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Una de las principales aplicaciones del cálculo diferencial es la optimización. Este es el proceso de encontrar valores máximos o mínimos de función para una relación dada. Hay cuatro tipos típicos de problemas que vamos a examinar en esta sección.
a) Optimización analítica: estos problemas suelen utilizar la fórmula de distancia para determinar el punto más cercano a una curva en particular.

b) Geometría/Optimización de Costos - estos problemas generalmente dan una caja o contenedor de una forma particular y piden determinar el costo de fabricación más económico dado un volumen particular o determinar el mayor volumen dado un costo particular.

c) Optimización de Distancia - estos problemas generalmente utilizan dos objetos que viajan en ángulo recto entre sí y determinan la distancia máxima o mínima entre los objetos.

d) Optimización de distancia/costo - estos problemas suelen estar enfocados en una situación en la que se pueden cortar dos distancias en ángulo recto con una diagonal en cierto punto para minimizar el costo o el tiempo.

Optimización analítica
\ [
d=\ sqrt {\ left (x_ {2} -x_ {1}\ right) ^ {2} +\ left (y_ {2} -y_ {1}\ right) ^ {2}}
\]
1) Exprese la distancia de un punto$(x, y)$ (en el primer cuadrante) en la gráfica de la parábola$y=x^{2}-4$ desde el punto (5,2) en función de$x$
2) Utilizar la gráfica de la función$d(x)$ distancia de la Parte I para determinar el punto de la gráfica de la parábola$y=x^{2}-4$ que está más cerca del punto (5,2)
3) Qué tan lejos está este punto del punto (5,2)$?$
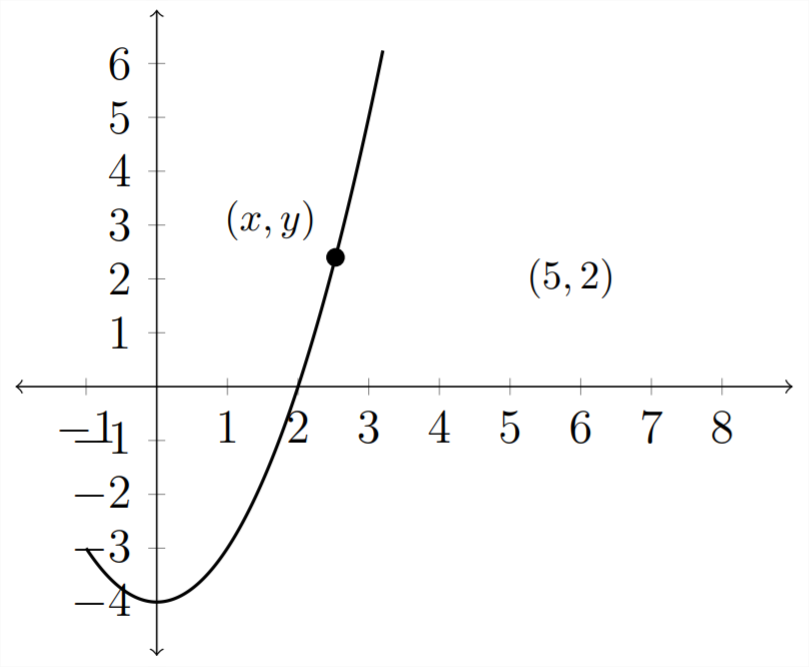
$clipboard_e77dd5a4742465589dcf46a0206809e77.png$
1) Usando la fórmula de distancia$d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}},$ podemos decir que cualquier punto de la curva$y=x^{2}-4$ es una distancia de:
\ [
d=\ sqrt {(x-5) ^ {2} + (y-2) ^ {2}}
\]
desde el punto$(5,2) .$ Porque la pregunta pide que esto sea expresado como una función de$x,$ debemos reemplazar la$y$ variable con una expresión equivalente que involucra$x$
\ [
\ begin {array} {c}
d=\ sqrt {(x-5) ^ {2} +\ left (x^ {2} -4-2\ right) ^ {2}}\
\ text {o}\\
d=\ sqrt {(x-5 ) ^ {2} +\ izquierda (x^ {2} -6\ derecha) ^ {2}}
\ end {array}
\]

2) La gráfica de esta función de distancia está a continuación:
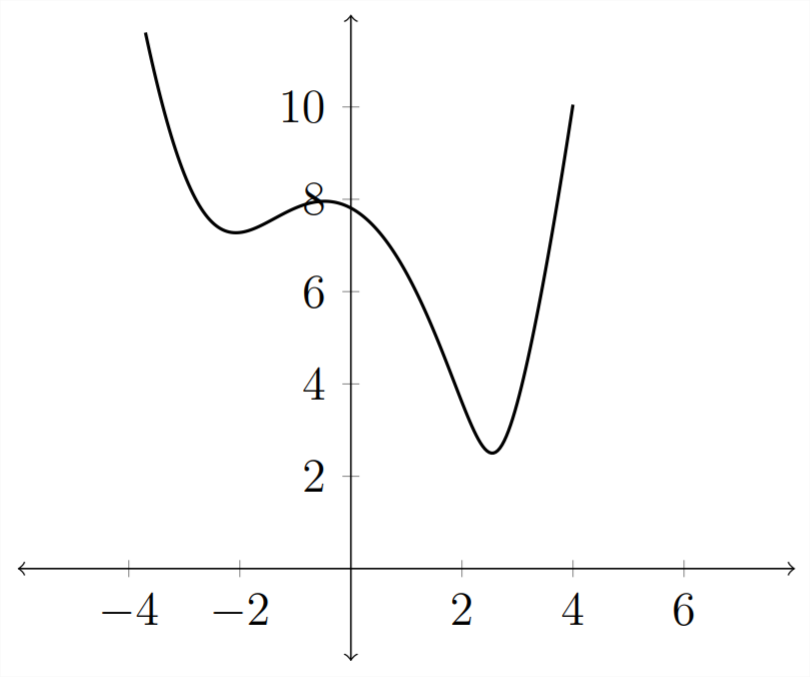
$clipboard_e3b603f080c13b1f6de005b109ebee647.png$
Obsérvese que en esta gráfica, el$x$ eje representa$x$ los valores de la gráfica original, pero el$y$ eje en esta gráfica es la distancia de un punto en la curva original desde el punto$(5,2) .$ Nosotros puede ver que esta función de distancia tiene un valor mínimo claro que ocurre entre$x=2$ y$x=4 .$ Podemos usar la calculadora gráfica para encontrar este valor - en Cálculo usaríamos álgebra para encontrar este valor.
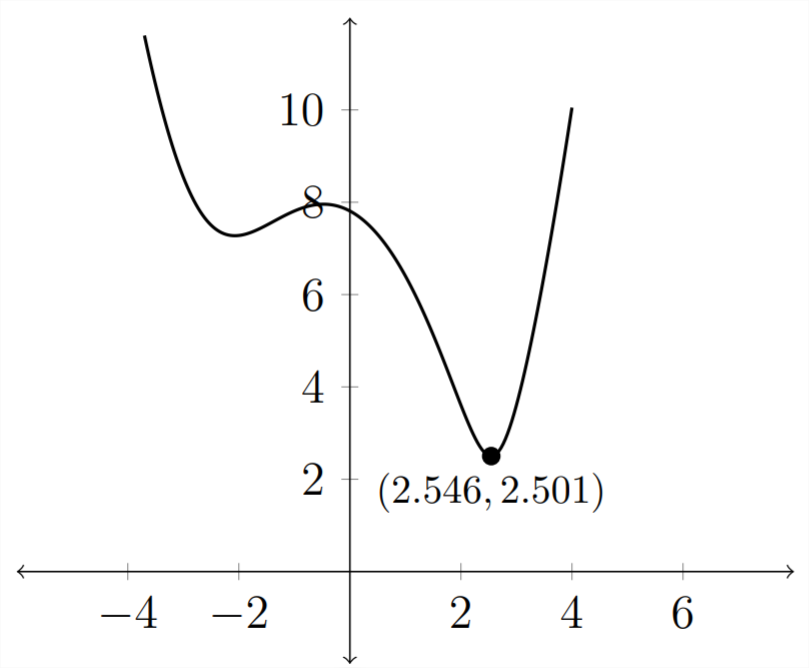
$clipboard_ed564b29313f15e8baf2048d0f743b1e1.png$
Ambos valores indicados en la gráfica son aproximados. El valor$x \approx 2.546$ indica el$x$ valor del punto en la curva original que está más cerca del punto (5,2) El$y \approx 2.501$ indica la distancia del punto desde el punto (5,2)
ya que el$x$ valor del punto en la curva original que está más cerca del punto (5,2) se trata de$2.546,$ eso significa que el$y$ valor es:
\ [
y=x^ {2} -4\ approx 2.546^ {2} -4\ approx 6.482-4\ approx 2.482
\]
Así que la respuesta para la Parte 2 es que (2.546,2.482) es el punto más cercano en la curva$y=x^{2}-4$ al punto (5,2)
3) Ya determinamos la distancia cuando encontramos el punto mínimo en la gráfica de distancia. La distancia es de aproximadamente 2.501 unidades.

Ejercicios$4.9(a)$
1) Dada la función$f(x)=4-x^{2}$, hallazgo$x$ y$y$ coordenadas del punto en la curva que está más cerca del punto$(7,3) .$ ¿Qué tan lejos del punto (7,3) está el punto que encontraste?
2) Dada la función$f(x)=6-x^{2},$ find$x$ y$y$ coordenadas del punto en la curva que está más cerca del punto$(1,1) .$ ¿Qué tan lejos del punto (1,1) está el punto que encontraste?
3) Dada la función$f(x)=x^{2}+2 x-5,$ find$x$ y$y$ coordenadas del punto
en la curva que está más cerca del punto$(-2,5) .$ ¿Qué tan lejos del punto (-2,5) está el punto que encontró?
4) Dada la función$f(x)=x^{2}-5 x+8,$ find$x$ y$y$ coordenadas del punto en la curva que está más cerca del punto$(-2,2) .$ ¿A qué distancia del punto (-2,2) está el punto que encontró?
5) Dada la función$f(x)=x^{3}-4 x^{2}+2 x+1,$ find$x$ y$y$ coordenadas del punto en la curva que está más cerca del punto$(2,1) .$ ¿Qué tan lejos del punto
(2,1) está el punto que encontraste?
6) Dada la función$f(x)=2 x^{3}-5 x-1,$ find$x$ y$y$ coordenadas del punto
en la curva que está más cerca del punto$(-2,8) .$ ¿Qué tan lejos del punto (-2,8) está el punto que encontró?
7) Un rectángulo tiene una esquina en el primer cuadrante en la gráfica de$y=16-x^{2}$ una esquina en el origen y las otras dos esquinas en el$x$ eje positivo y el$y$ eje positivo.
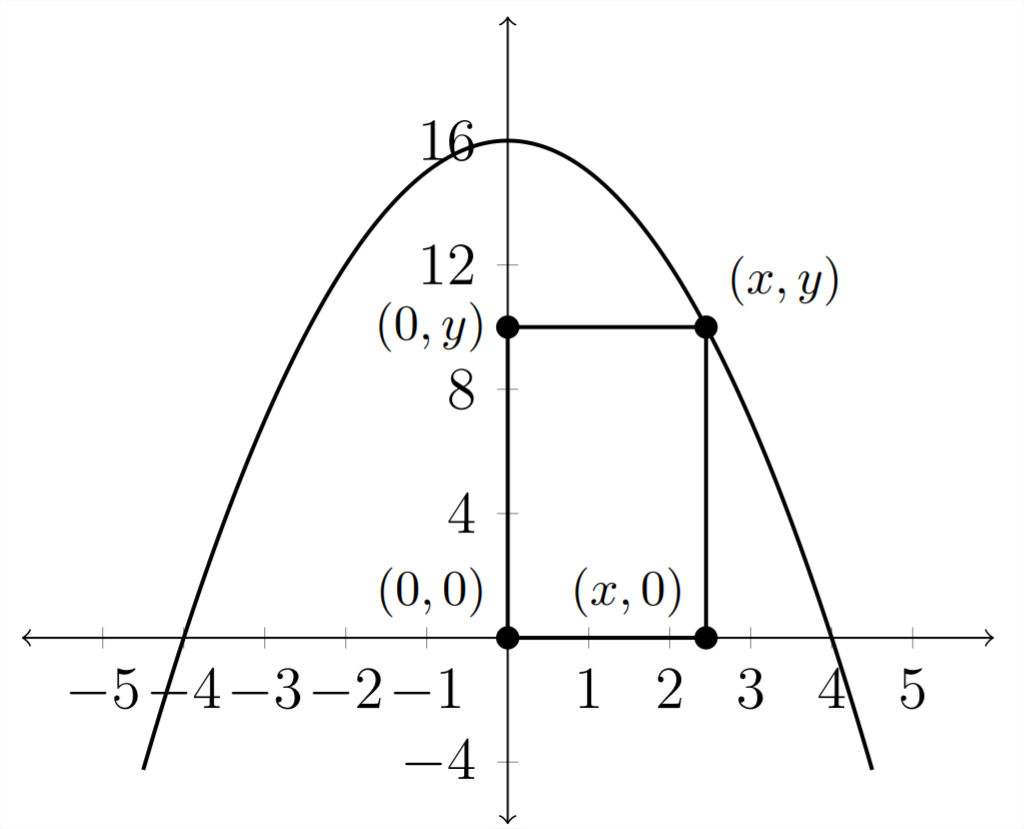
$clipboard_edd7efcab8fd1498b082c528ca5f3c240.png$
a) Expresar el área$A$ del rectángulo en función de$x$.
b) ¿Por qué valor de la zona$x$ es mayor?
c) ¿Cuál es el área máxima?

8) Un rectángulo se inscribe en un semicírculo de radio 5 de manera que dos esquinas estén en el$x$ eje y dos esquinas estén en el semicírculo.
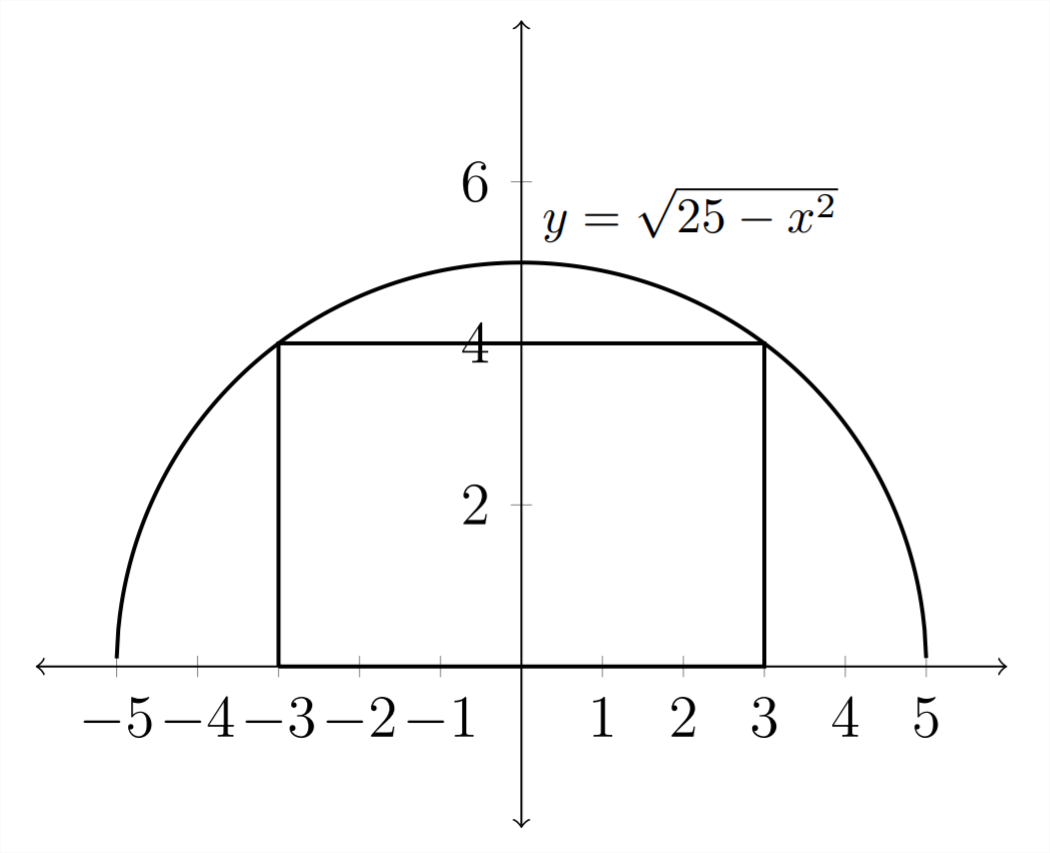
$clipboard_e652563c536276598174806a09ab77b0e.png$

La fórmula para la gráfica del semicírculo es$y=\sqrt{25-x^{2}}$
a) Expresar el área$A$ del rectángulo en función de$x$.
b) ¿Por qué valor de la zona$x$ es mayor?
c) ¿Cuál es el área máxima?

Optimización de Geometría/Costo
Una caja cerrada con base cuadrada está construida a partir de material que cuesta$\$ 1$$\mathrm{ft}^{2}$ por los cuatro lados y la parte inferior y$\$ 5$ por$\mathrm{ft}^{2}$ para la parte superior. ¿Cuáles son las dimensiones de la caja de mayor volumen para la que se puede construir$\$ 72 ?$

Hay dos temas con los que estamos trabajando en este problema: el volumen de la caja y la superficie de la caja. El volumen de la caja es importante porque eso es lo que buscamos maximizar. El área de superficie de la caja es importante porque eso es lo que controlará el costo de la caja - observe que los costos se dan en términos de$\mathrm{ft}^{2}$ o pies cuadrados que está relacionado con el área de superficie.

La caja tiene una base cuadrada, pero la altura es alguna otra dimensión -$h$. Entonces el volumen de la caja será largo$*$ ancho$*$ alto, pero como la caja tiene una base cuadrada el largo y ancho serán los mismos -los llamaremos$x$. De esto vemos que el volumen se puede expresar como:
\ [
v=x * x * h=x^ {2} h
\]
Para el costo de la caja, necesitamos conocer la superficie. Cada lado de la caja debe estar incluido - la base y la parte superior tienen la misma área ($x^{2}$) porque ambos son cuadrados que son$x$ unidades en cada lado. Los cuatro lados de la caja son todos rectángulos que son$x$ por$h$ unidades. Eso significa que cada uno tiene un área de$x * h-$ por lo que los cuatro serían$4 * x * h$ o$4 x h$
Esto hace que el área superficial de la caja:
\ [
S=2 x^ {2} +4 x h
\]
El costo de la caja entonces será:
\ [
C=x^ { 2} (\ $1) +x^ {2} (\ $5) +4 x h (\ $1)
\]
Aquí vemos que el uno$x^{2}$ se multiplica por$\$ 1,$ porque el fondo costará$\$ 1$ por$\mathrm{ft}^{2},$ pero el otro$x^{2}$ se multiplica por$\$ 5,$ porque los costos superiores$\$ 5$ por$\mathrm{ft}^{2}$. Los cuatro lados: también$4 x h$ se multiplica por\ $1.

Entonces, nuestra fórmula final para el costo es:
\ [
C=6 x^ {2} +4 x h
\]
pero ya sabemos que queremos gastar$\$ 72$ en la caja, así podemos decir que:
\ [
72=6 x^ {2} +4 x h
\]
Esto quiere decir que:
\ [
\ begin {array} {c}
\ frac {72-6 x^ {2}} {4 x} =h\\
\ text {o}\
\\ frac {18} {x} -1.5 x=h
\ end {array}
\]
La razón por la que esto es importante es que nos permitirá expresar el volumen de el cuadro en términos de$x .$ Recuerda que el volumen era:
\ [
v=x^ {2} h
\]
así que ahora podemos ver que:
\ [
\ begin {array} {c}
v=x^ {2}\ left (\ frac {18} {x} -1.5 x\ right)\\
\ text {o}\\
V=18 x-1.5 x^ {3}
\ end {array}
\]

La gráfica para esta función está a continuación:

Podemos ver en la gráfica que el volumen máximo dado un costo de$\$ 72$ será cuando la base de la caja sea de 2 pies por 2 pies. El volumen será$24 \mathrm{ft}^{3}$ y la altura será de 6 pies. Entonces la respuesta a la pregunta es$2 \mathrm{ft} \times 2 \mathrm{ft} \times 6 \mathrm{ft}$

Ejercicios$4.9$ (b)
1) Un contenedor de almacenamiento rectangular con una parte superior abierta tiene un volumen de$10 \mathrm{m}^{3}$. La longitud de su base es el doble del ancho. Material para los costos base$\$ 10$ por metro cuadrado. Los costados requieren material que cuesta$\$ 6$ por metro cuadrado. Encuentre el costo de los materiales para el contenedor de este tipo más barato.
2) Un póster debe contener$108 \mathrm{cm}^{2}$ de material impreso, con márgenes de$6 \mathrm{cm}$ cada uno en la parte superior e inferior de la página y$2 \mathrm{cm}$ en cada lado de la página. ¿Cuál es el costo mínimo del cartel si se va a hacer de material que cuesta$\$ 0.20$ por centímetro cuadrado?
3) Si$1200 \mathrm{cm}^{2}$ de material está disponible para hacer una caja con una base cuadrada y una parte superior abierta, encuentre el mayor volumen posible de la caja.
4)$\quad A$ caja con base cuadrada y parte superior abierta debe tener un volumen de$32,000 \mathrm{cm}^{3}$ Encuentra las dimensiones de la caja que minimice la cantidad de material utilizado.
5) Una ventana normanda tiene la forma de un semicírculo encima de un rectángulo para que el diámetro del semicírculo sea el mismo que el ancho del rectángulo. Dado que el perímetro de la ventana debe ser$30 \mathrm{ft}$, encuentre las dimensiones de la ventana que admitan la mayor cantidad de luz solar (maximizar el área).
6) Una caja rectangular sin tapa debe ser hecha de material que cuesta$\$ 0.50$ por pie cuadrado. El ancho de la base es de 5 pies y tendrá un volumen de$6 \mathrm{ft}^{3}$. ¿Cuáles son las dimensiones de la caja que minimiza el costo? ¿Cuál es el costo de esta caja?
Área superficial de un cilindro$=2 \pi r^{2}+2 \pi r h$
Volumen de un cilindro$=\pi r^{2} h$
7) Una lata cilíndrica con una parte superior estará hecha de 200 pulgadas$^{2}$ de estaño. ¿Cuál sería la altura y el radio de la lata de volumen máximo?
8) Una lata cilíndrica con una parte superior tendrá un volumen de$500 \mathrm{cm}^{3}$. Si los lados y el fondo cuestan$\$ 0.002$ por cuadrado$\mathrm{cm}$ y los costos superiores$\$ 0.0035$ por cuadrado$\mathrm{cm},$ encuentran las dimensiones de la lata menos costosa que tendrá un volumen de$500 \mathrm{cm}^{3}$ ¿Cuánto cuesta hacer esta lata?

Optimización de distancia
Un barco está a 10 millas al este de una boya y navega hacia el oeste, hacia la boya a 12 mph. Otro barco se encuentra a 10 millas al sur de la misma boya y navega hacia el norte, también hacia la boya a 7 mph.
a) Escribir una función que represente la distancia entre las dos naves en términos
$t,$ del tiempo transcurrido en horas.
b) Graficar la función y determinar el valor de$t$ cuando los barcos están más cerca juntos. ¿Qué tan lejos están los barcos en este momento?
Redondear el valor de$t$ a las 100 de hora más cercanas.
Redondear la distancia hasta la décima de milla más cercana.
Aquí hay un diagrama que representa el problema:
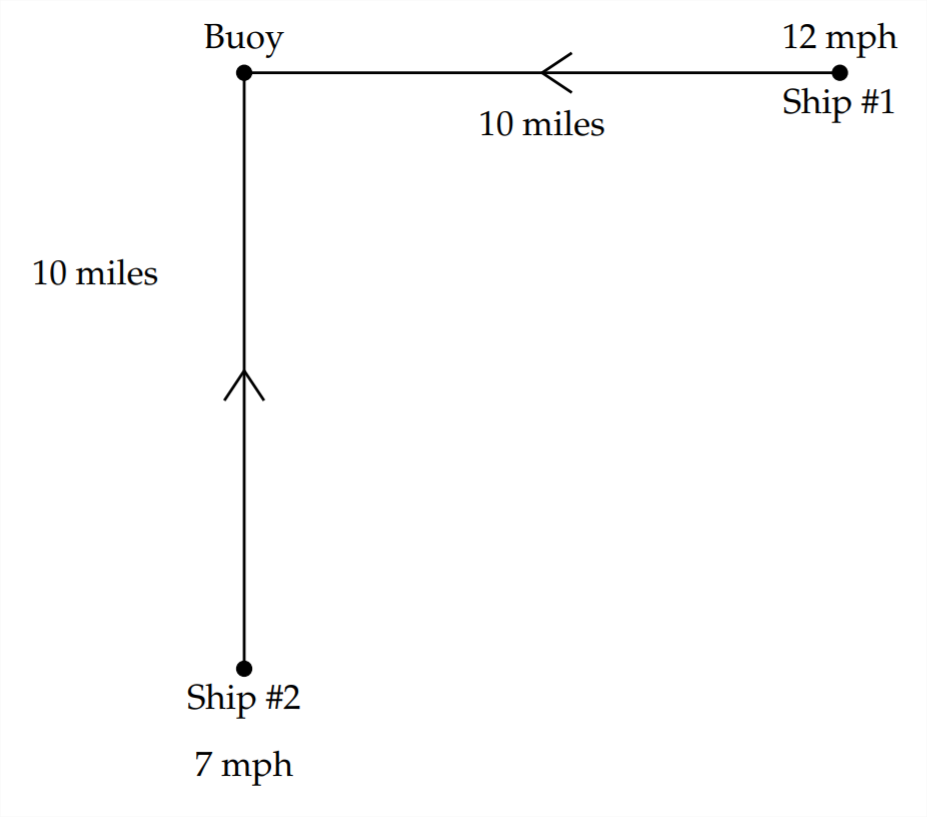
$clipboard_eb9e00c7329a1f1f445410b591e4a3238.png$
La distancia entre los dos barcos se mide a lo largo de la diagonal. Debido a que esto crea un triángulo rectángulo, podemos usar el Teorema de Pitágoras para representar la distancia entre las naves.
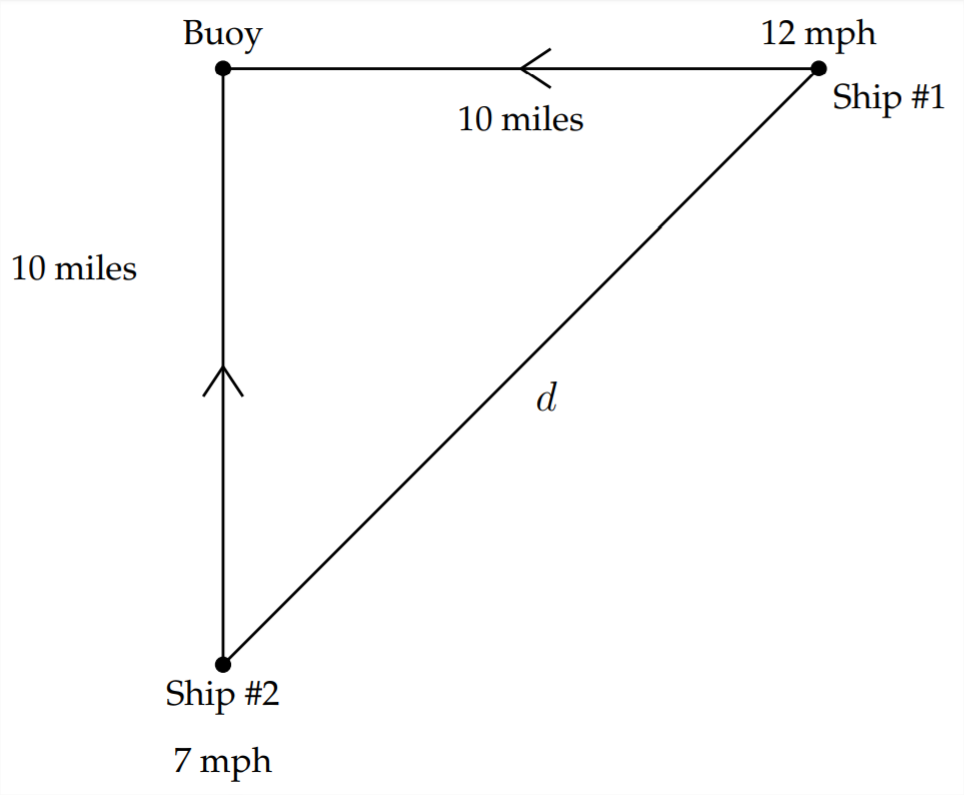
$clipboard_e74bee849393b3df7ec6a2df683b51955.png$

En este caso las patas del triángulo rectángulo comienzan como 10 millas, pero se acortan a medida que los barcos se acercan a la boya. Para el Buque #1, la distancia disminuye 12 millas cada hora, esto significa que el primer barco pasará por la boya en menos de una hora. La distancia entre el Barco #1 y la boya se puede representar como$(10-12 t)$ dónde$t$ está el número de horas que se pasan viajando. Del mismo modo, la distancia entre el Barco #2 y la boya se puede representar como$(10-7 t)$

Entonces, usando el Teorema de Pitágoras, podemos representar la distancia entre las naves en cualquier momento dado como:
\ [
d^ {2} =( 10-7 t) ^ {2} + (10-12 t) ^ {2}
\]
o
\ [
d=\ sqrt {(10-7 t) ^ {2} + (10-12 t) ^ {2}
\]

El gráfico de esta función de distancia se ve así:
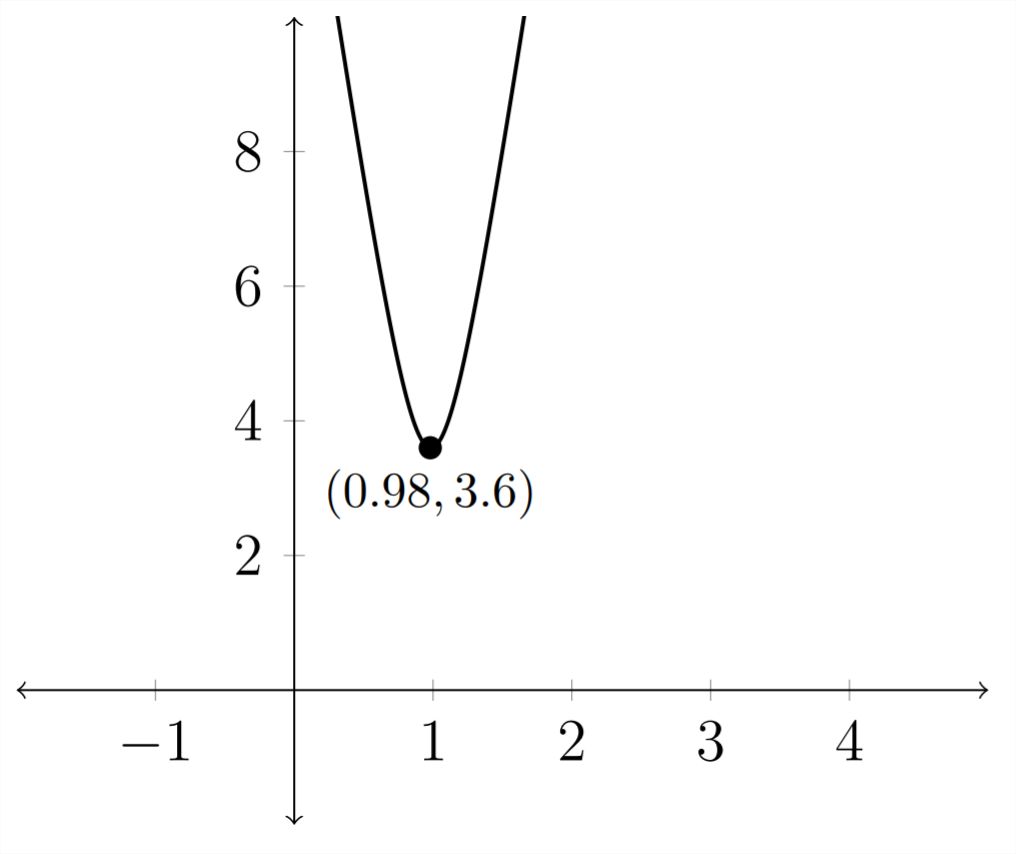
$clipboard_eb88a12d9da8ec2238680e51797cd86e5.png$
El punto mínimo en el gráfico de distancia indica el tiempo en el que los barcos están más cerca juntos. Después de viajar por 0.98 horas, los barcos estarán a unos 3.6 millas de distancia. Entonces comenzarán a distanciarse más.

Ejercicios$4.9(c)$
1) Un corredor comienza a correr hacia el norte desde un punto dado corriendo a 5 metros por segundo. Al mismo tiempo, un segundo corredor se dirige hacia el este desde el mismo punto de partida, corriendo a 8 metros por segundo. Representar la distancia entre los corredores en función$t,$ del tiempo transcurrido. ¿Cuánto tiempo tardarán los corredores en estar a 150 metros de distancia?

2) Un corredor comienza a correr hacia el norte desde un punto dado corriendo a 10 metros por segundo. Al mismo tiempo, un segundo corredor se dirige hacia el este desde el mismo punto de partida, corriendo a 7 metros por segundo. Representar la distancia entre los corredores en función$t,$ del tiempo transcurrido. ¿Cuánto tiempo tardarán los corredores en estar a 200 metros de distancia?

3) En$1 \mathrm{pm}$ una bicicleta está a 9 millas al norte de una heladería y viaja hacia el sur (hacia la heladería) a 15 mph. Al mismo tiempo, otro ciclista se encuentra a 2 millas al este de la heladería y viaja hacia el este (lejos de la heladería) a 12 mph. Representar la distancia entre los ciclistas en cualquier momento dado después$1 \mathrm{pm}$. ¿A qué hora es mínima la distancia entre los pilotos? ¿Qué tan lejos están en este punto?

4) Un automóvil sale de una intersección de cuatro vías a las 9:15am, viajando hacia el sur a 70 mph. Al mismo tiempo, otro automóvil se encuentra a 65 millas al oeste de la intersección viajando hacia el este a 55 mph. Expresa la distancia entre los dos autos en función del tiempo desde que salieron de la intersección. ¿A qué hora están los autos más cercanos entre sí? ¿Qué tan lejos están el uno del otro en este momento?

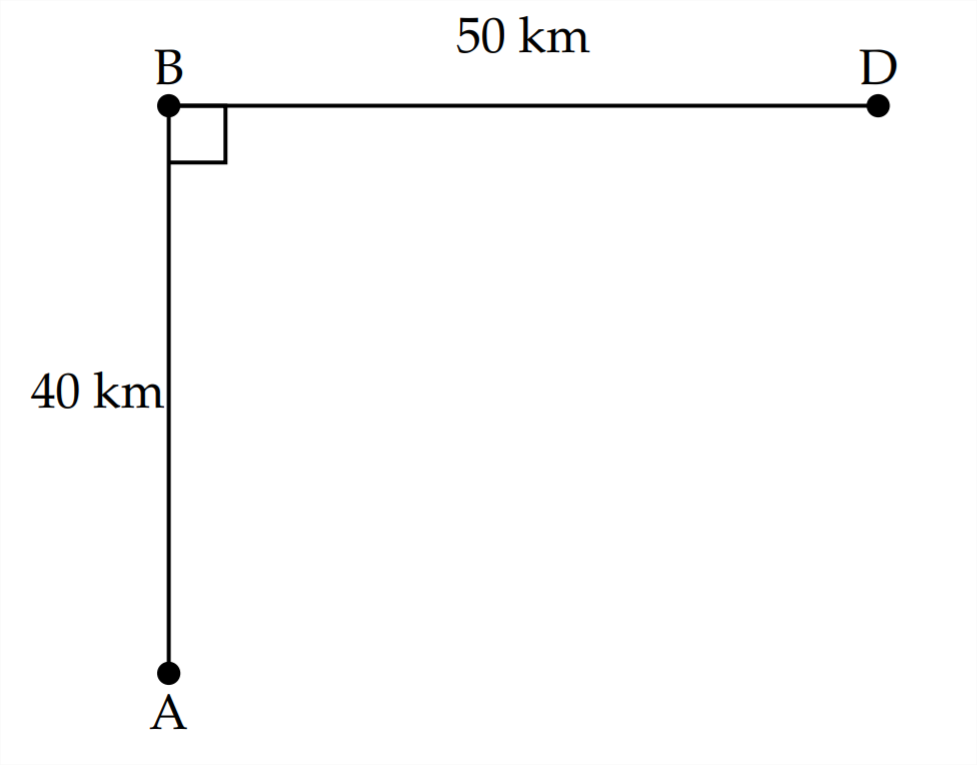
Al mediodía, un buggy de dunas se encuentra en el desierto en el punto que$A$ se indica a continuación. $A$El punto es$40 \mathrm{km}$ de una carretera pavimentada, que cubre los puntos$50 \mathrm{km}$ entre$\mathrm{B}$ y$\mathrm{D}$

Si el buggy de dunas puede recorrer 45 kph en el desierto y 75 km/h en la carretera, ¿dónde es el mejor lugar para que el conductor salga del desierto y gire hacia la carretera con el fin de minimizar el tiempo de viaje?

¿A qué hora llega el conductor a Point$D$ asumiendo que sigue el camino para un tiempo mínimo de viaje?
$clipboard_e68c08dcf1e02297969accf18f1362a8d.png$
Una opción es que el buggy duna pueda viajar en línea recta de A a B (a 45 kph) y luego viajar por la carretera pavimentada de$\mathrm{B}$ a$\mathrm{D}$ (at$75 \mathrm{kph}$). Esto tomaría$1.5 \mathrm{hrs}$
Otra opción es que el buggy de dunas viaje directo de la A a la D a 45 kph. La distancia aquí es aproximadamente$64 \mathrm{km}$ (encontrada usando el Teorema de Pitágoras). Eso significa que el tiempo de viaje sería de aproximadamente 1.423 hrs.

La optimización aquí dice que, si el buggy de duna viajara parte del camino en el desierto (a lo largo de una diagonal) y el resto del camino en la carretera pavimentada, entonces podría haber un tiempo mínimo que es más corto que las 1.423 hrs. tomaría ir recto de$\mathrm{A}$ a$\mathrm{D}$
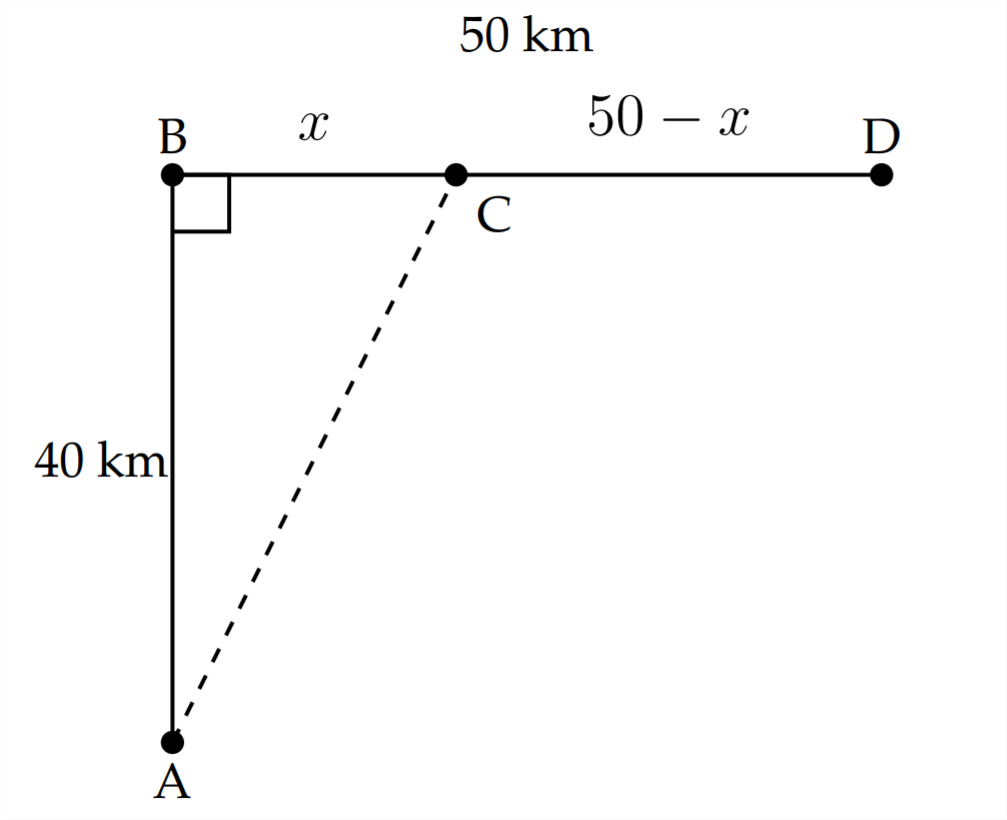
$clipboard_e2295318b695f61ac8d9ab88bb2320a63.png$
Si expresamos la distancia entre$\mathrm{B}$ y$\mathrm{C}$ como$x,$ entonces la distancia entre$\mathrm{C}$ y D será$50-x$. La distancia recorrida en el desierto es la distancia de A a$C$ y esta se encuentra utilizando el Teorema de Pitágoras.
\ [
\ overline {A C} =\ sqrt {40^ {2} +x^ {2}} =\ sqrt {x^ {2} +1600}
\]
desde$d=r * t,$ entonces el tiempo que toma viajar una distancia dada será$\frac{d}{r}=t$
En el caso de este problema el tiempo para viajar de A a C es:
\ [
t_ {1} =\ frac {\ sqrt {x^ {2} +1600}} {45}
\]
El tiempo para viajar de$C$ a$D$ es:
\ [
t_ {2} =\ frac {50-x} {75}
\]
Entonces, el tiempo total de viaje será:
\ [
t=t_ {1} + t_ {2} =\ frac {x^ {2} +1600} {45} +\ frac {50-x} {75}
\]

La gráfica de esta función está a continuación:
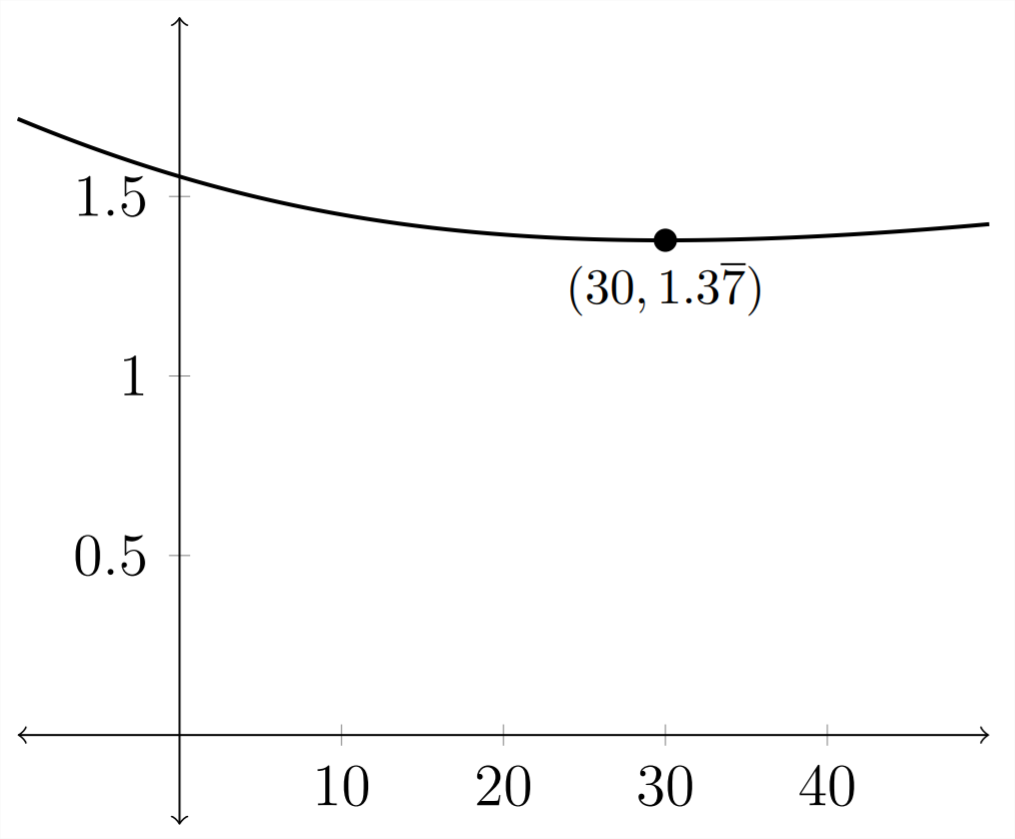
$clipboard_e2412b12667e8bcb0ec65a5eda119bfbd.png$
Es difícil de ver, pero hay un mínimo para la gráfica donde$x=30$ y$t=1.3 \overline{7}$

Ejercicios$4.9(d)$
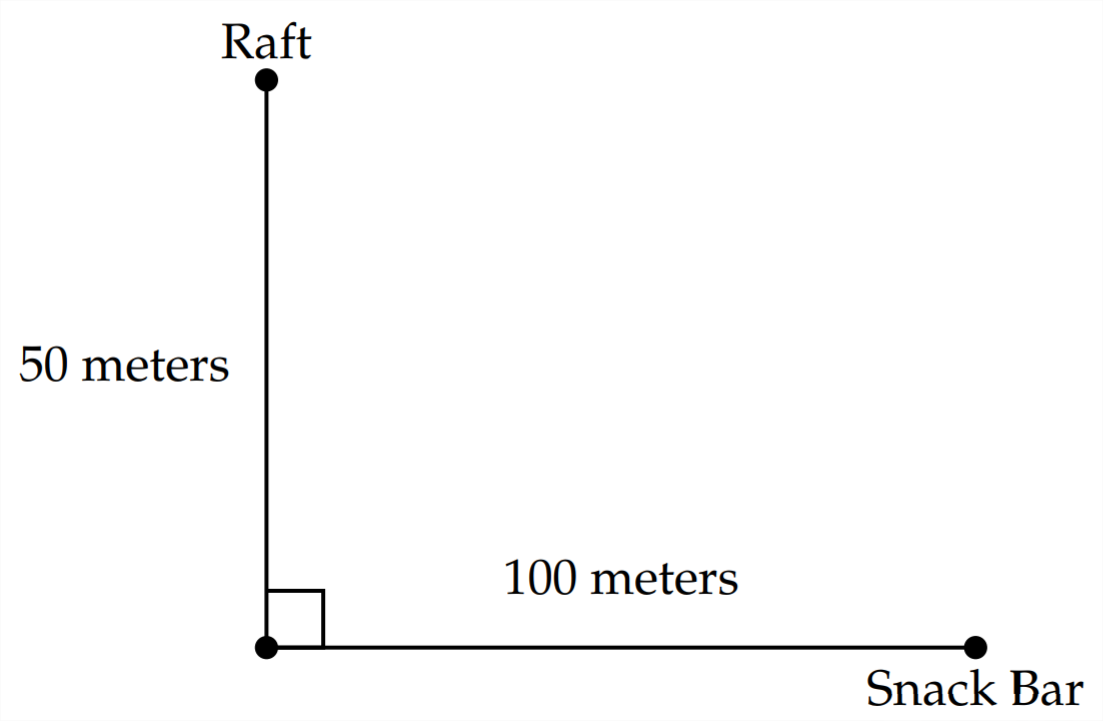
1) Una mujer quiere nadar a la orilla desde una balsa que se encuentra a 50 metros de la costa y luego correr hacia el snack bar ubicado a 100 metros por la costa. La mujer nada 1 metro por segundo y corre a 5 metros por segundo. ¿En qué parte de la costa debe nadar para minimizar su tiempo de viaje?
$clipboard_ebe8f9a73ae39955568b3ebb25b6ab7ee.png$
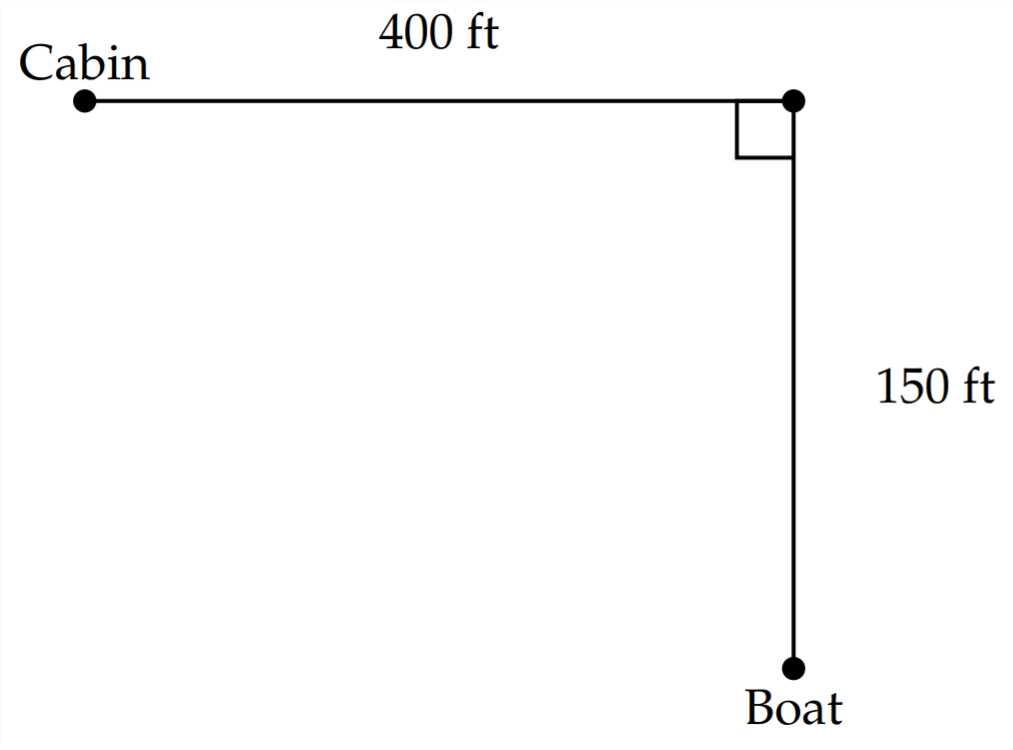
2) Un hombre se encuentra en un bote en un lago$150 \mathrm{ft}$ desde la orilla. Quiere regresar a su cabaña. Está$400 \mathrm{ft}$ bajando de la costa desde la cabaña. Planea remar hasta la orilla, dejar el bote donde aterriza y luego correr el resto del camino hasta la cabaña. Si rema 7 pies por segundo y corre 15 pies por segundo, ¿dónde debería playar el bote de remos para minimizar el tiempo de viaje?
$clipboard_e757f167e6800177b3679c37301149d65.png$
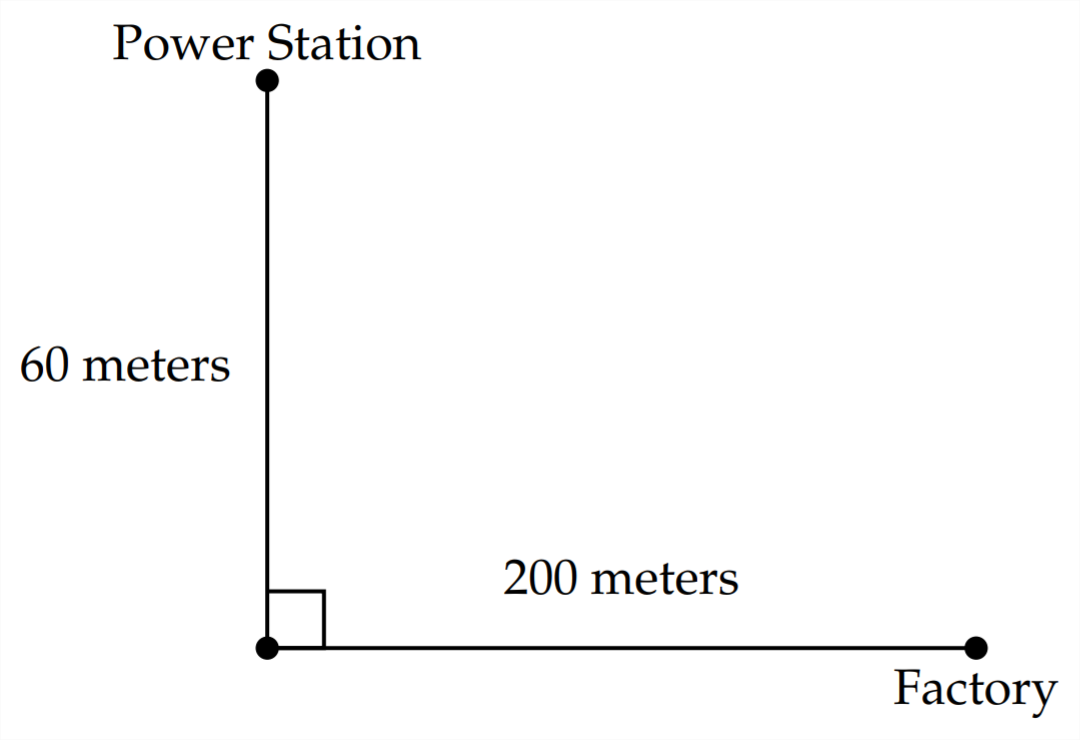
3) Una central eléctrica y una fábrica se encuentran en lados opuestos de un río que tiene
60 metros de ancho. La fábrica se encuentra a 200 metros del punto en la orilla justo enfrente de la central eléctrica. Se debe colocar una línea eléctrica entre la central eléctrica y la fábrica. Cuesta$\$ 25$ por metro hacer correr el cable en el río y$\$ 20$ por metro correr el cable en el terreno. ¿Cuánto del cable se debe tender en el río y cuánto se debe colocar en tierra para minimizar el costo? ¿Dónde debería desembarcar el cable? ¿Cuál es el costo mínimo?
$clipboard_eaaccebcfb6fc58fd516de178e73e5110.png$
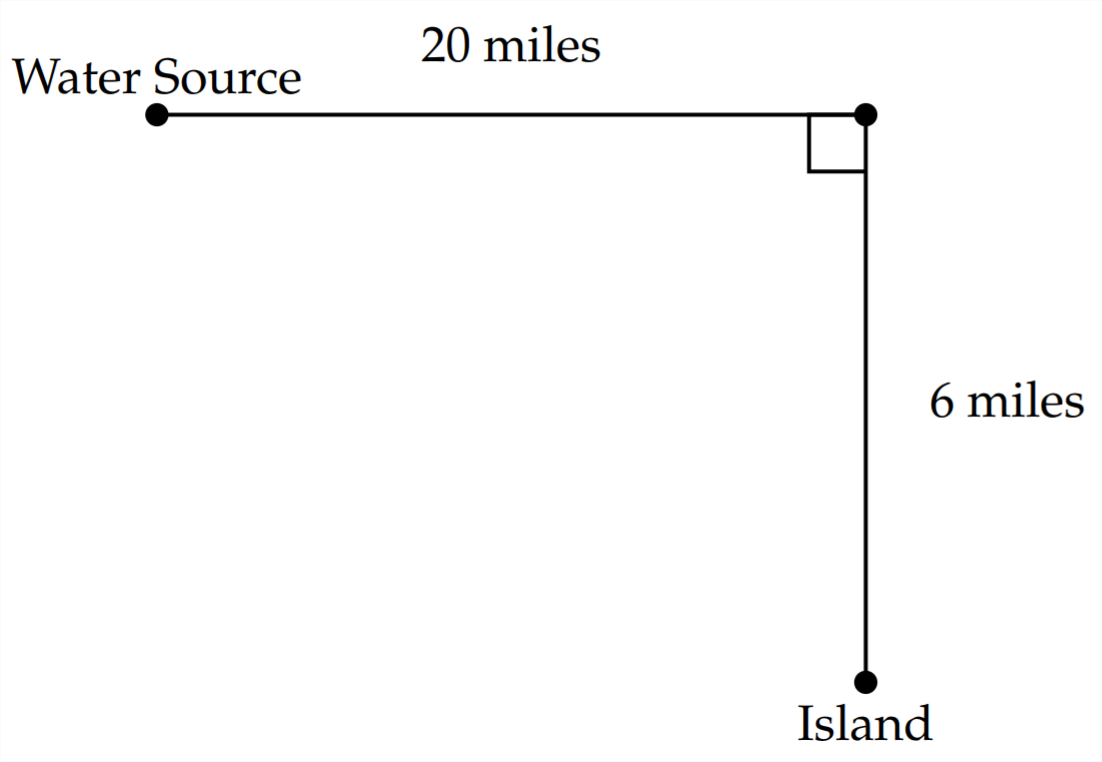
4) Se está construyendo un oleoducto de agua dulce a una isla que se encuentra a 6 millas del continente. La fuente de agua se encuentra a 20 millas por la costa desde el punto de la orilla más cercano a la isla. El costo de tender la tubería a lo largo de la costa es$\$ 8,000$ por milla, mientras que el costo de colocar la tubería en el agua es$\$ 12,000$ por milla. ¿Cuánto de la tubería se debe colocar en el agua y cuánto se debe colocar en tierra para minimizar el costo? ¿Dónde debería salir el oleoducto de la orilla? ¿Cuál es el costo mínimo?
$clipboard_e29d8f6003738a82bac68edfa3b657840.png$